1. Introduction

This paper is an extension of work originally presented in 2019 International Conference on Advanced Technologies for Communications (ATC) in Ha-Noi, Viet-Nam [1].

Quantum computation is problem solving and data computation using a system based on quantum mechanics, which is an effort to generalize classical computation. Quantum information systems could be able to transmit data fundamentally securely and solve complex problems better than classical information systems [2]. In 1994, Peter Shor invented a quantum algorithm for factoring integers into prime factors which runs on polynomial time [3]. In addition, in 1996 Lov Grover devised a quantum search algorithm for searching unstructured databases [4]. Hence, quantum algorithms promised big improvements on performance in comparison to classical computation; consequently, many problems have been considered in quantum computation [5]. However, the effects from imperfectly applied quantum gates, decoherence, and other quantum channel noise would affect the practical design of quantum computation. To overcome such problems, quantum error correction code (QECC) based on the theory of classical error correction code, was developed to protect quantum states from noise environment [6]. Since the first QECC was discovered by Shor [7], the method of containing redundancy to circumvent the no-cloning theorem has been popularly used. Therefore, the importance of QECC on practical building of quantum computer is no longer in doubt.

Cryptography is the research of secure communication techniques which allow only sender and intended receivers to view the content of shared messages. With the advantages of quantum mechanism such as entanglement and no-cloning theory, quantum cryptography is an application of quantum mechanics to cryptography. The first quantum cryptography protocol is BB84 which is invented by Dr. C. H. Bennett [8], it is public-key cryptography. In 1980, a novel private key cryptography protocol named Shamir no-key protocol is invented where the sender and receiver do not exchange the key, however the protocol requires the sender and receiver to have their own private keys for encrypting and decrypting the messages with the hard and complex on computation. Since quantum mechanism with no-cloning theorem which can be used to improve no-key protocol; then, in 2002 a quantum cryptography protocol based on Shamir’s no-key protocol is considered [9]. In [10], in combination with Hill-cipher algorithm, the quantum no-key protocol was proven to be a scheme for secure direct quantum communications wherein the information is encrypted into a binary string and each bit is exchange between sender and receiver.

The main result of this research is to propose a new quantum no-key protocol which a single quantum state to establish the transfer of many information bits. In addition, the qubit needs to be protected from noise for the correct quantum state exchanged between Sender and Receiver. Hence, we emerge the proposed protocol with quantum error correction codes to establish the secure communication channel which can against the quantum noise, decoherence, and unwanted environments. The organization of this paper is as follows. In Section 2, the basic of quantum computation and quantum error correction codes are reviewed. In Section 3, we first propose the quantum no-key protocol; then, the emerging quantum no-key protocol with error correction code is discussed. Then, the conclusion is presented.

2. Preliminaries

2.1.  Basic of Quantum Computations

Quantum theory uses qubit to represent information, the quantum systems with two levels such as: two polarization states of photons, two energy levels of atoms, etc. A qubit  is considered to be found in the both basis states  and  where the probability value we saw that qubit at state   is  and at state  is . It is superposition concept of a qubit, which is one of a main property of quantum information since the amount of information which presented in qubits are no limitation [11,12]. A qubit can be displayed in matrix form as,

According to norm condition for a qubit on the Bloch sphere space, the complex numbers a and b satisfy the equation . A n qubits system is constructed by multiple tensor products of some other qubits, it is given as follows,

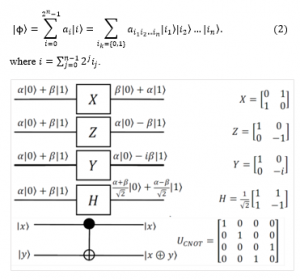
Figure 1: Basic quantum gates with matrices presentation

The most important thing when we consider a system is the transformation between states among. In quantum information system, quantum states are changed by the quantum gates. Mathematically, quantum gates could be expressed via the matrix representation. The constraints for quantum gates are that they are revertible, it means that the quantum gate which transform the state  back to state , would satisfy . That type of matrix U is called unitary matrix. Figure 1 shows the most important quantum gates with these matrices form. Pauli channel of quantum system consists of four basic elements, namely X, Z, Y, and I (identity matrix). Any operation and errors acting on qubit could be represented as their combination. Hence, we have three types of errors which can affect a qubit, they are bit flip, phase flip, and their combination. In general, the error operators that effect on  n qubits have the form: where .

2.2.  Basic of Quantum Error Correction Codes

The simplest QECC is three qubits repetition code that can correct only one type error, namely bit flip or phase flip [13]. The QECC can be simulated by quantum circuit model; they are showing in the Figure 2, 3 for three qubits repetition code. The difference between them are on the Clifford gate has been used: X=HZH and Z=HXH.

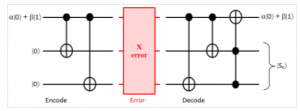
Figure 2: Quantum circuit for X-error 3- repetition code

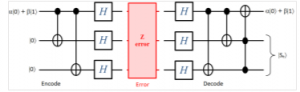
Figure 3: Quantum circuit for Z-error 3- repetition code

The explanation for these quantum circuits are described as follows. First, the quantum circuit starts with the initial information, we extend it to the 3-qubits system via helps of ancilla 2 qubits of zeros. After transformation by encoding step, the logical states or encoded qubits are created. Here, two basis states of codewords for 3-qubit are defined as follows,

Then, the quantum gates as previous mentioned must to be declared. Here, the quantum gates X, Z, and two new types of CNOT gates are used. The tensor product was used to extend one qubit to many qubits system.

To extend the first full quantum code, Shor code for 9 qubits is created by Shor, which use both bit-flip correction and phase-flip correction and can correct bit-flip, phase-flip, and their combination [14]. To do so, for one qubit is protected against phase-flip we need extend it to codeword of three qubits. Then, each qubits of that three-qubits need to extend to three-qubits to protect against bit-flip error. Hence, the quantum circuit starts with the initial information, we extend it to the 9-qubits via helps of ancilla 8 qubits of zeros, after transformation by encode step, the logical states or encoded qubits are created. Here, two basis states of codewords 9-qubits repetition as well as

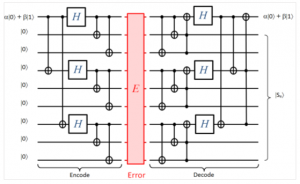Figure 4: Quantum circuit for Shor code

Using matrices transformation, the states after applying error and decoding can be found. The final states show us the correction state can be recovered the syndrome tell us which error has applied to logical states. The full quantum circuit for Shor code is given in Figure 4.

       Generally, the quantum error correction code can be denoted as [[n,k,d]] where n is length of codeword, k is length of information bits, and d is  minimum distance which corresponds to number of error  the code can be detected and corrected. The parameter for Shor code at Figure 4 is [9,1,3], and it is the first quantum error correction code. Since the first proposed of Shor code, many novel quantum codes with diverse parameters have been proposed [15,16], they are called quantum stabilizer codes.  The most important of quantum stabilizer codes are that they could be constructed by binary formalism, then the quantum circuit model are easy created which points are discussed detailly in [12].

3. Proposed System

3.1.  Quantum no-key protocol

Quantum no-key protocol was invented by S. Kak [9], which is an emerging of classical no-key protocol with quantum mechanism. In this system, Sender and Receiver do not share the public key, they have their own private keys. The private key on quantum no-key protocol is an unitary transformation which has following form:

The private keys in (6) are commutative to each other, it means . If Sender or Receiver choose  for its private encryption key, the corresponding decryption key will be   since .

We assume that Sender and Receiver want to share the quantum state , the protocol is proceeded as Figure 5. The detail of each steps are as follows,

1. Sender randomly choice private encryption key, apply it to quantum state to get . Then, transfer that encrypted state to Receiver.
2. Assume that there is no noise on the channel, Receiver gets the correct recipient from Sender, . Receiver also randomly choice its private encryption key, apply it to current quantum state to get . Then, transfer back encrypted quantum state to Sender.
3. Assume that there is no noise on the channel, Sender gets correct recipient from Receiver, Sender applies the decryption private key according to step 1, , then current quantum state is . Sender transfers its state to Receiver.
4. Assume that there is no noise on the channel, Receiver gets the correct recipient, . Then, Receiver can get the original message by applying decryption private key according to step 3, . Finally, Receiver gets . Sender and Receiver successfully exchange original quantum state.

The original quantum no-key protocol just mentions the exchange one bit, 0 or 1, for each round by attached it to quantum state,  or . In next subsection, we consider the proposed system for multi-bits transfer for each round. Then, it reduces the time of transferring long message.

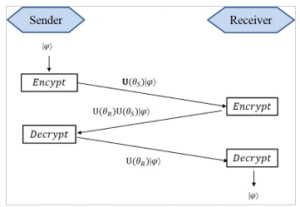
Figure 5: Quantum no-key protocol

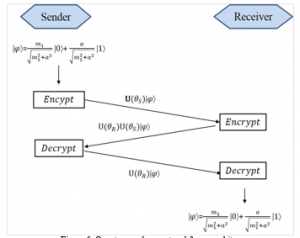
Figure 6: Quantum no-key protocol for many bits

3.2.  Proposed quantum no-key protocol for many bits’ transfers

We assume that Sender and Receiver wish to exchange the binary string , where each  is binary string of length l, that means the total length of binary string Sender and Receiver want to exchange is . We denote that binary string  has the decimal value . The proposed protocol is as follows.

1. Sender and Receiver first exchange the binary string by using the quantum no-key protocol. As analysis on Section 3.1, since  has length l, the cost of using quantum no-key protocol for successfully recipient is l. We denote a is the decimal value corresponding to binary string .
2. For binary string , Sender first encodes to the quantum state: | ñ= | ñ+  | ñ, where  is the decimal value of binary string . The detail of using quantum no-key protocol is shown in Figure 6. We assume that there is no error from quantum channel. Then, Receiver gets correct quantum state | ñ=  | ñ+  | ñ. Since the value of a is known before, Receiver will know exactly   via measurement. Finally, Receiver will get binary string . The cost for exchange binary string  between Sender and Receiver is one time using quantum no-key protocol.
3. For remaining binary string , the same procedure as Step 2 is taken. The cost for successfully recipient is .

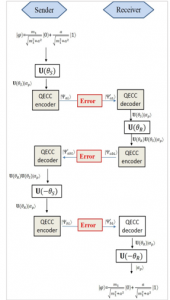
Figure 7: Quantum no-key protocol with error correction code

3.3.  Analysis the cost of proposed protocol

For whole binary string , if we use original quantum no-key protocol, it is mentioned in [10], we need to use that protocol  times, since the length of this binary string is . In contrast, if we use proposed protocol, we need the cost is  This shows that our propose system is suitable to transfer a long binary string.

In this subsection, we still assume that the quantum channel is perfectly. Hence, Sender and Receiver will transfer quantum state successfully to each other.  In next Section, we will consider the channel have error and we propose the using of quantum error correction code to reduce that problem.

• Proposed quantum no-key protocol with error correction codes

It is proved that in quantum channel quantum state can interact with unwanted environment, which can make bit-flip, phase-flip, or both of them, bit-phase flip. In quantum no-key protocol, we need to transmit quantum state three times, if the error or environment is bad, the result of our system will be go down. Quantum error correction code (QECC) is the solution to solve that problem. The key ideas of QECC is that the quantum state, length k, is extended to have large length, length n > k, where n – k redundant qubits we called them parity-check part. The novel QECC is discussed in Section 2.2 where we mention repetition codes for bit-flip and phase flip error, Shor codes for any error, bit-flip, phase-flip, or their combination.

Figure 7 shows the detail step of using QECC on quantum no-key protocol. The difference between Figure 7 and Figure 6 is that the QECC encoder and QECC decoder are inserted three times, since we have three times of transmission between Sender and Receiver.

4. Conclusion

In this research, we have proposed the quantum no-key protocol for many bits transfer which is suitable for long binary string transmission. The cost analysis is given in detail to show the effective of proposed system. In addition, the emerging of QECC on that proposed system is promised the way for secure transmission against the unwanted quantum channel.

Conflict of Interest

The authors declare no conflict of interest.

Acknowledgment

This work was supported by the Research Program through the National Research Foundation of Korea (NRF-2019R1A2C1005920).

1.  D. M. Nguyen, S. Kim, “A quantum three pass protocol with phase estimation for many bits transfer”, in 2019 International Conference on Advanced Technologies for Communications (ATC), Viet Nam. https://doi.org/10.1109/ATC.2019.8924514
2.  D. M. Nguyen, S. Kim, “Multi-Bits Transfer Based on the Quantum Three-Stage Protocol with Quantum Error Correction Codes”, International Journal of Theoretical Physics 58 (6), 2043-2053, 2019. https://doi.org/10.1007/s10773-019-04098-4
3.  P.W. Shor, “Algorithms for quantum computation discrete logarithms and factoring”, IEEE Computer Society Press. 124-134, 1994. 10.1109/SFCS.1994.365700
4.  L. Grover, “Quantum mechanics helps in searching for a needle in a haystack”, Phys. Rev. Lett. 79, 325, 1997. https://doi.org/10.1103/PhysRevLett.79.325
5.  A. M. Zidan et.al, “A Quantum Algorithm Based on Entanglement Measure for Classifying Boolean Multivariate function into Novel Hidden Classes”, Results in Physics, 15, 102549, 2019. https://doi.org/10.1016/j.rinp.2019.102549
6.  D. M. Nguyen, S. Kim, “Quantum stabilizer codes construction from Hermitian self-orthogonal codes over GF(4)”, Journal of Communications and Networks 20 (3), 309-315, 2018. https://doi.org/10.1109/JCN.2018.000043
7.  P.W. Shor, “Scheme for reducing decoherence in quantum computer memory”, Physical Review A, 52, 2493, 1995. 10.1103/physreva.52.r2493
8.  C. H Bennett, G Brassard, “Quantum cryptography: Public key distribution and coin tossing”, International Conference on Computers, Systems & Signal Processing, Bangalore, India, Dec 9-12, 1984. http://researcher.watson.ibm.com/researcher/files/us-bennetc/BB84highest.pdf
9.  S. Kak, “A three-stage quantum cryptography protocol”. Found Phys Lett 19, 293, 2006. https://doi.org/10.1007/s10702-006-0520-9
10.  A.A. Abdullah et.al, “A realizable quantum Three-Pass protocol authentication based on Hill-Cipher algorithm”. Math. Probl. Eng., 2015, 481824, 2015. https://doi.org/10.1155/2015/481824
11.  D. M. Nguyen, S. Kim, “New Constructions of Quantum Stabilizer Codes Based on Difference Sets”, Symmetry 10 (11), 655, 2018. https://doi.org/10.3390/sym10110655
12.  D. M. Nguyen, S. Kim, “Construction and complement circuit of a quantum stabilizer code with length 7”, in 2016 Eighth International Conference on Ubiquitous and Future Networks (ICUFN), 2016. https://doi.org/10.1109/ICUFN.2016.7537043
13.  D. M. Nguyen, S. Kim, “The fog on Generalized teleportation by means of discrete-time quantum walks on N-lines and N-cycles”, Modern Physics Letters B 33 (23), 1950270, 2019. https://doi.org/10.1142/S0217984919502701
14.  D. M. Nguyen, S. Kim, “A novel construction for quantum stabilizer codes based on binary formalism”, International Journal of Modern Physics B, 03/2020. https://doi.org/10.1142/S0217979220500599
15.  D. M. Nguyen, S. Kim, Quantum stabilizer codes based on a new construction of self-orthogonal trace-inner product codes over GF(4), International Journal of Modern Physics B, 34(5), 2050017, 02/2020. https://doi.org/10.1142/S0217979220500174
16.  D. M. Nguyen, S. Kim, New construction of binary and nonbinary quantum stabilizer codes based on symmetric matrices, International Journal of Modern Physics B, 33(24), 1950274, 2019. https://doi.org/10.1142/S0217979219502746

(Click Here)

(Click Here)