1. Introduction

With the development of internet communication technology, the amount of transmission of various types of multimedia data including images is increasing. This trend is also true for medical data. Medical diagnostic images are transmitted over wired and wireless networks. These medical images are transmitted via the Internet or the hospital intranet which include many important information about the patient’s personal information. However, current hospital intranet lacks reliable security equipment. In addition, on the Internet, not only malicious manipulation of information by malicious attackers, but also leakage of information on unauthorized third parties is very serious. Medical image encryption is an effective technique that can protect not only medical images but also important personal information of patients from these various attacks.

Some existing traditional encryption techniques, such as International Data Encryption Algorithm (IDE), AES and DES are well suited for text data security, but not for bulk data encryption such as digital images. This is because images have inherent properties with large data sizes, high redundancy, and strong imagery correlation.

Since chaos function is ergodic and sensitive to initial conditions and parameters, it is a powerful function that can effectively encrypt various types of data. These chaotic functions are easy to implement with microprocessors and personal computers [1]. Therefore, the chaos map-based encryption algorithm is suitable for mass multimedia data encryption because it can design a fast encryption system at low cost.

      Recently, methods of medical image encryption based on chaotic function have been studied by many researchers [2-10]. Mao et al. proposed a cryptographic algorithm that not only maintains a high level of security but also speeds up image encryption using a map that extends the Baker map in three dimensions [2].  In [3], Dai and Wang proposed logistic maps and Chebyshev maps based a medical image encryption. They overcame the problem that logistic maps-based cryptographic systems are inadequate for medical image cryptography because of their low key space and low security. Wang et al. designed a color image cryptographic system that used the chaotic function to simultaneously encrypt the three colored components of the given image and allow these components to affect each other [4]. Fu et al. proposed an alternative bit shuffling algorithm in which pixel value mixing effects can be contributed by the replacement and the permutation process. That chaotic based algorithm reached existing cryptographic security levels with fewer rounds of performance [5]. Zhang and Luo proposed chaotic CA based an image encryption algorithm [6]. The algorithm proposed by them was used a two dimensional logistic function to encrypt images and then applies two dimensional CA on the initial encrypted image. In [7], Nandi et al. noted that the unique and powerful nature of CA is the ease of hardware implementation and the large number of rules that apply to the CA, making it impossible for an attacker to find a combination of rules that is the key to extracting the original information. So they proposed a CA-based cryptographic algorithm to substitute pixel values of original image. However, this method needs to be supplemented because it is weak to noise and data loss that may occur for image transmission.

Jeong et al. gave an encryption algorithm for medical image. They used a maximum length one-dimensional CA with complemented rules and a modified chaotic cat map. They changed pixel values of the given image using a nonlinear key sequence generated by a one-dimensional CA with complemented rules. And then they changed pixel positions of the image with pixel value changed using the modified chaotic map. However, the modified chaotic maps they designed have an unmaintained weakness of the image size required by the chaotic cat map [8]. Therefore, there is a need to overcome the weaknesses of the modified two-dimensional chaos function in [8] and to efficiently encrypt color images. In order to enhance security, a PRNG that can generate a nonlinear key sequence is required.

In this paper, we design CoCA for medical image encryption. CoCA is made up of a nonlinear CA and a linear 90/150 maximum length CA. And we give a secure and trusty encryption scheme based on CoCA and three dimensional generalized chaotic map. The proposed algorithm consists of two phases. The first phase encryption process that changes  pixel values ​​of a given image using two CoCAs. The second phase is to change the position of each pixel in the image encrypted using the three dimensional generalized chaotic cat map that can change with effect the position of pixels not only in two dimensions horizontally and vertically but also in color plane three colored channels simultaneously. We show the stability and high reliability of the given color medical image cryptosystem through detailed analysis and various statistical experimental tests.

2. Preliminaries

2.1.  Cellular Automata

Von Neumann [11] introduced CA at first and Wolfram [12]  developed CA. CA is very important mathematically for modelling complex behavior. CA is composed of an array of basic memory called cells, and its state is updated to the following state depending on the state of neighboring cells of radius 1 including itself. These CAs are classified into one-dimensional CA, two-dimensional CA, and the like according to the arrangement of the cells. In addition, according to the number of cells that affect when one cell of the CA is updated to the following state, it is classified as 3-neighbor CA, 5-neighbor CA, 9-neighbor CA. And it is classified into NBCA, PBCA, and IBCA according to boundary condition of both ends of CA. The CA used in this paper is an NBCA. The CA used in this paper is the simplest CA that is the 1-D 2-state 3-neighbor NBCA.

The state transition function f, which decides the following state of the cell, is a mapping in which the domain is {000, 001, 010, … 111} and the airspace is {0,1}. f is expressed as follows.

, where   is the jth  cell state of CA  at the time t. As shown in Table 1, the CA transition rule is a decimal representation of the numerical value of the following state determined according to the state of the current neighbor. For example, if the following state function value for {111, 110, 101, … , 010, 000} is ‘01010010’, the converted value is 82, so the given transition rule is 82. Table 1 shows the transition rule numbers of the state transition function according to the following state of the cell with respect to the state of the current neighbor cells.

Table 1: The Transition Rule Number according to the Following State of the Cell

Nbd state	111	110	101	100	011	010	001	000	RN.
Following state	0	0	0	1	1	1	1	0	30
	0	1	0	1	1	0	0	1	90
	1	0	0	0	1	1	0	1	141
	1	0	0	1	0	1	1	0	150
	1	0	1	0	1	1	0	0	172

When the state transition function is expressed as a Boolean function, a rule consisting only of XOR logic is called a linear rule, and a rule consisting of XOR logic and XNOR logic is called a complemented rule. And rules that include OR and AND logic are called nonlinear rules. In Table 2, rules 30, 141, and 172 are nonlinear rules, and rules 90 and 150 are linear rules. A CA having a linear rule applied to all cells of a CA is called a linear CA, and a CA to which a nonlinear rule is applied is called a nonlinear CA. The linear CA can express a function for obtaining the following state as a matrix, which is called the state transition matrix .

Table 2: The Boolean functions for Rules 30, 90, 141, 150 and 172

RN	Boolean functions
30
90
141
150
172

From now on we use a CA using only the transition rules 90 and 150 which is called 90/150 CA.  of the 90/150 CA is as following [13, 14] :

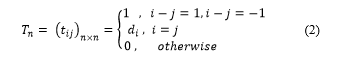The linear CA C can express a function for obtaining the following state as a matrix . We call    the state transition matrix of C. The CA applicable to the cryptographic algorithm must be reversible and decryptable. This reversible CA must be unique to the previous state for a given state. Therefore, the inverse of T must exist. This means that the determinant of T must not be zero. If  is the current state of C and   is the following state of , then  can be obtained by  and  as follows [15] :

An n-cell reversible CA C is referred to as Maximum Length CA (MLCA) when the minimum p satisfying  for  of C is , where  is the  identity matrix. For example, a four-cell CA with transition rules <90,150, 90,150> is MLCA with period 15.

2.2.  Three Dimensional Generalized Chaotic Map

For a metric space X with metric d, a function F: X →X that satisfies the following is said to be sensitive to initial conditions:

if there is a  such that for every   and  there exists   with d(x, y) <  and  for k .

Chaos is associated with randomness, disorder, and entropy. Arnold Cat Map is a simple function proposed by Russian mathematician Arnold that can randomly transform the composition of image pixels. This transformation causes the image to be very complicated when this transformation is repeated by changing the position of the pixels without changing the size of the image. This function is represented by a two-dimensional matrix

Jeong et al. designed an encryption algorithm for medical color image using the map modified (5) [8]. However, (5) only changes the pixel position of the gray image because it can change the pixel position of the two-dimensional image. Therefore, in order to effectively protect color images, methods of extending from the 2-D chaotic cat map to a 3-D chaotic cat map have been proposed [17, 18]. A 3-D chaotic cat map is gotten by the following operations using the  identity matrix:

Since     for each , .

3. Proposed Algorithm

Now we design an algorithm for encrypting medical images. Figure 1 shows a block diagram of the proposed algorithm. The medical image encryption algorithm proposed in this paper consists of two phases. The proposed algorithm consists of alternate and shuffling phases, and the pixel shuffling phase repeats n rounds to increase the security level of the encryption system.

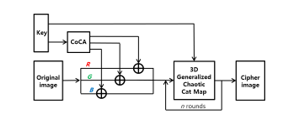Figure 1: Block diagram of a new color image encryption system with substitution and shuffling phases

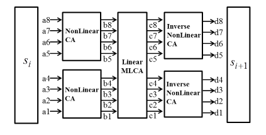Figure 2: The Structure of CoCA

3.1.  Substitution Phase

To generate an effective key image we design an effective PRNG. This PRNG is constructed as shown in Figure 2 by the combination of nonlinear reversible CA  and linear maximum length CA . This PRNG is called CoCA. When , a shared key, is the initial value of CoCA, the following state is . And .  Therefore,  obtained by repeatedly applying CoCA n times to  satisfies . Therefore, even if  is not an MLCA, if  is an MLCA, the CoCA becomes a nonlinear MLCA. The algorithm proposed in this paper generates key images using two CoCAs  and . The (i, j) pixel of the key image generated by  and  is represented .  can be expressed as (9):

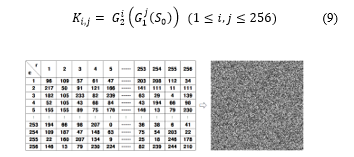Figure 3: The procedure of generating a key image using two CoCAs

Figure 3 shows the procedure of generating a key image from two CoCAs. This process divides the shared key value 8 bits  in half and performs state transitions through 4 cell nonlinear reversible CA , and then combines them into 8 bits again. The combined 8-bit values are once again transitioned using 8-cell linear MLCA . This transitioned result is then divided in half and converted to the final state by the inverse of  to produce pixel values. First, each pixel of the first row of the key image is a key sequence generated using , and pixels of each column of the key image are generated by  using the pixel value generated by  as the initial value.

3.2.  Shuffling Phase

The result of the XOR combining of the key image generated by two CoCAs and the original image is very effective because it results in the randomly changing the pixel value of the given image. However, if the encrypted image is damaged by unexpected noise or deliberate deletion attacks in the process of transmitting the digital image, the damaged part remains completely lost when the encrypted image is decrypted. Therefore, in order to design a cryptographic algorithm that is resistant to such attacks, in this paper, the final cryptographic image is generated by mixing the pixel positions of the image encrypted by the key image using a generalized 3-D chaotic cat map. Each pixel in the image has a gray level value from 1 to 255 for the R, G, and B components. Therefore, the total number of bits required to represent a color image of size M × M is M × M × 3 × 8. Each pixel position of a color image can be represented by (row, column, color component). In the image shuffling phase, we use the L in (8) to change not only the position of the rows and columns of pixels but also the positions of the components of R, G, and B using a generalized 3-D chaotic cat map. Mathematically, the pixel shuffling phase is represented by (10).

In (10), if each row of  is , then   , , where M is the multiple of 3.

3.3.  Color Medical Image Encryption Algorithm

      Table 3 shows a color medical image encryption algorithm Col_Medi_Encryp_Algorithm. This algorithm is a color image encryption algorithm that merges the encryption phases proposed in sections 3.1 and 3.2.

Table 3: Col_Medi_Encryp_Algorithm

Function 1 : CoCA state transition Def CoCA(Image, rule_table.nonlinear, rule_table.MLCA, Rule_table.Inverse) For (i, j, k) in Image_Index(row, column, color) a = rule_table.nonlinear(Image[i, j, k] //16) b = rule_table.nonlinear(Image[i, j, k]%16) Image[ i, j, k ] = a*16+b number  = key.MLCA For (i, j, k) in Image_Index(row, column, color) Key_Image[ i, j, k ] =  ( (number∧rule_table.MLCA) ⊕ (number//2) ⊕ (number*2)) mod 256 Image = Image ⊕ Key_Image mod 256 For (i, j, k) in Image_Index(row, column, color) a = rule_table.Inverse(Image[ i, j, k ] // 16) b = rule_table.Inverse(Image[ i, j, k ] % 16) CoCAed_Image[ i, j, k ] = a*16 + b Return CoCAed_Image

Function 2 : 3D generalized chaotic cat mapping Def 3D_Chaotic_cat_map(Image, cat_map_matrix, times) Construct (Index_list(row,column,color) of Image) For i from 1 to times: cat_mapped_Index_list = matrix_vector_multiply(cat_map_matrix,  Index_list(row, column, color) of Image) For ( i, j, k ) in Image_Index(row, column, color) Cat_mapping_Image[i, j, k] = Image[cat_mapped_Index_list([i, j, k])] Return Cat_mapping_Image

Algorithm  : Col_Medi_Encryp_Algorithm Input : Image, rule_table.nonlinear, rule_table.MLCA, Rule_table.Inverse,  cat_map_matrix, times Output : Encrypted_Image Encrypted_Image  = CoCA(Image, rule_table.nonlinear, rule_table.MLCA, key.MLCA, rule_table.Inverse) Image  = 3D_Chaotic_cat_map(Image, cat_map_matrix, times)

3.4.  Key Scheming

The variables that can be used as keys are: (1) Transition rules and initial values, which are the components of the two CoCAs require for the generation of a key image in the substitution phase. (2) Parameters of the proposed chaotic cat map used in the shuffling phase of mixing pixel positions.

4. Safety analysis of the proposed system

By the proposed cryptosystem we present the performance results in this section. Since medical images often have a high color bias, it must be shown whether the results are suitable for such images. Medical X-ray images were adopted as basic images suitable for such safety analysis.

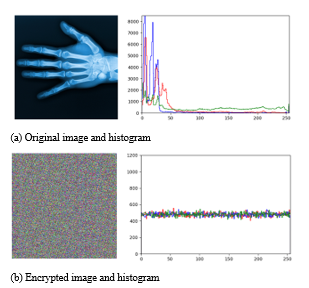Figure 4: The histograms of the original image and the encrypted image

Table 4: Entropy and Comparison Analysis of Methods

Methods	Entropy
Proposed Algorithm	7.99837
Wang et al. [19]	7.99763
Wu et al. [20]	7.99722

4.1.  Histogram Analysis

Figure 4- (a) shows the original medical image and histogram used to perform encryption. Most of the given medical images occupy black, and the original image actually has a very high bias at pixel value zero.

Figure 4- (b) shows the image and histogram that encrypted the original image using the proposed encryption system. Although the original medical image is a high deflection image, the pixel values of the encrypted image are very evenly distributed. This means that the distribution of colors is spread evenly according to the result of the encryption system. This proves to be safe for traditional statistical methods.

4.2.  Information Entropy Analysis

A cryptographic image with high uncertainty means it is safe from accidental information attacks. In other words, the encrypted image must have a high degree of uncertainty with respect to information analysis. High uncertainty can be expressed through information entropy. Information entropy is as shown in (11).

Where m is the information source and p(m) is the probability for finding the original value for each bit. Table 4 shows the information entropy of the encrypted image obtained by the proposed encryption system. In addition, the information entropy of cryptographic images obtained through several other cryptographic systems is also shown. In an 8-bit RGB format image, the closer to 8, the higher the uncertainty. According to Table 4, it is shown that the proposed cryptosystem, like the previously proposed cryptosystems, provides high uncertainty in the cryptographic image.

4.3.  Correlation Coefficient Analysis

      Correlation coefficients between pixel values indicate how distributed the image is in a particular color. The correlation coefficient is expressed as in (12) below:

where x and y represent the values of two different positions in the RGB color space. In the correlation coefficient analysis, two positions are examined by randomly extracting two adjacent pixels horizontally, vertically, and diagonally. We examined random 2500 pairs of pixel values for each color channel of the image for correlation coefficient analysis. After repeating this test 400 times, the mean of all the extracted correlation coefficients was examined.

Table 5: Correlation Coefficients of an original image and an encrypted image

Methods	Horizontal	Vertical	Diagonal
Original image	0.9785	0.9730	0.9543
Proposed Algorithm	0.0019	0.0048	-0.0048
Zhang et al. [21]	0.0035	0.0037	0.0023

      We provide the results of the correlation coefficient analysis obtained in the above-mentioned method in Table 5. Correlation coefficient analysis results are for the original image, the encrypted image using the proposed encryption, and the encrypted image based on previous studies. The value obtained according to (12) is distributed from -1 to 1. The closer to 1, the higher the correlation coefficient, which means that adjacent pixels have almost the same value. The correlation coefficients of the original image are close to 1 in either direction. This means that pixel values ​​in adjacent locations almost always have a similar color. Closer to zero means that there is almost no correlation. The correlation coefficient of the encrypted image using the proposed encryption system is very close to zero in all directions.

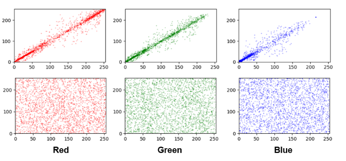Figure 5: Scatter plots of horizontal direction of each color channels of

the plain image and cipher image

The encrypted image indicates that it has different values ​​at any adjacent positions, and it is difficult to find out what the original image is by color analysis. Figure 5 shows a scatter plot in the horizontal direction for each color channel in the normal and password images. It can be seen from the figure that the proposed encrypted image has little correlation between adjacent pixels.

4.4.  Sensitive Analysis

      An adversary can make a differential attack by analyzing different encrypted images obtained from a single key. Therefore, the slightest change of the image in the cryptosystem should cause a huge change as a whole. Analysis of these changes is called sensitivity analysis, and there are two well-known methods: The number of changing pixel rate (NPCR)

and the unified averaged changed intensity (UACI). NPCR and UACI for analyzing the proposed encryption algorithm are defined as the following (13) and (14):

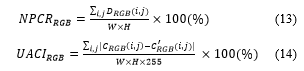where  represent the size of the plain image. In (14),  denotes a difference between pixel values of the ith rows and the jth columns of an image, and   and  are of an original image and an encrypted image, respectively. In (13),    and ,

Table 6: NPCR and UACI of encrypted images of different Images due to a small difference

Color	NPCR (%)	UACI (%)
R	99.6347	33.6082
G	99.6404	33.6748
B	99.61445	33.5853

NPCR and UACI of medical cryptographic color images through the proposed cryptographic system are provided in Table 6. The NPCR of over 99% indicates that the microscopic image changes almost entirely. In cryptography, about 33% of the UACI indicates that the distribution of differences in pixel values is even. Figure 6 shows encrypted images with different 1 bit of original image data.

Figure 6: Encrypted images with different 1 bit of original image data

4.5.  Key Space Analysis

      The number of available keys determines the size of the key space. To create a key image, we need two CoCAs consisting of a nonlinear CA and a 90/150 MLCA. In 8-cell CA, the number of rules is the number of cases applicable to each cell, which is . the number of rules that can be used for two CoCAs is . The number of keys required for the initial value is . We can control the variables a and b for the pixel shuffling process of the 3D cat map, and the number of variables is  where N is the size of one direction of the image to be shuffled. If N = 256, the key space size is  in the proposed encryption scheme. Therefore, the proposed medical cryptography algorithm has a sufficiently large key space that the information eavesdropper cannot launch brute force attacks.

4.6.  Restore for data corruption

Data stored in the database may be damaged by abnormal external interference. Image encryption algorithms must be able to resist these abnormalities. Experiments are conducted to test the resistance to noise and data loss. Figure 7 shows that even when abnormal data corruption occurs in an encrypted image, the original image is sufficiently resilient to be identified.

Figure 7: Restoration of damaged cipher image

5. Conclusion

In this paper, we proposed a safe and reliable color medical image algorithm based on CoCAs and three dimensional generalized chaotic cat map. The proposed algorithm had a very large key space and improved the nonlinearity of the key stream generated by using CoCAs. In addition, in the pixel shuffling phase of the encrypted image, the pixel positions of the image were changed together with the R, G, and B planes simultaneously, and thus we implemented a cryptosystem having a very strong resistance to noise and data loss. The detailed analysis of the encrypted images obtained by the proposed algorithm showed the high security and stability of the new medical color image encryption system. In the future, we will study high-speed image encryption suitable for encrypting large-capacity images and study various CA-based PRNG designs.

Acknowledgment

This paper is the revised and expanded version of a paper entitled “Color Medical Image Encryption using 3D Chaotic Cat Map and NCA” presented at 2019 10th IFIP International Conference on New Technologies, Mobility and Security (NTMS), Canary island, Spain, 24-26 June 2019. And this research was supported by the Tongmyong University Research Grants 2018(2018A046).

1.  X. Wang, L. Liu and Y. Zhang, “A novel chaotic block image encryption algorithm based on dynamic random growth technique,” Opt. Laser Eng., 66, 10-18, 2015 https://doi.org/10.1016/j.optlaseng.2014.08.005
2. Y.B. Mao, G,R, Chen, S.G. Lian, “A novel fast image encryption scheme based on 3D chaotic baker maps,” Int. J. Bifurcation Chaos, 14(10), 3613-3624, 2004. https://doi.org/10.1142/S021812740401151X
3.  Y. Dai, X. Wang, “Medical image encryption based on a composition of logistic maps and Chebyshev maps”, in 2012 IEEE International Conference on Information and Automation, Shenyang, China, 210-214, 2012. http://doi.org/10.1109/ICInfA.2012.6246810
4. X. Wang, L. Teng, X. Qin, “A novel color image encryption algorithm based on chaos,” Signal Process., 92(4), 1101-1108, 2012. https://doi.org/ 10.1016/j.sigpro.2011.10.023
5. C. Fu, W. Meng, Y. Zhan, Z. Zhu, F.C.M. Lau, C.K. Tse, H. Mae, “An efficient and secure medical image protection scheme based on chaotic maps,” Comput. Biol. Med., 43(8), 1000-1010, 2013. https://doi.org/10.1016/ j.compbiomed.2013.05.005
6. S. Zhang and H. Luo, “The Research of Image Encryption Algorithm Based on Chaos Cellular Automata,” J. Multimedia, 7(1), 66-73, 2012. https://doi.org/10.4304/jmm.7.1.66-73
7. S. Nandi, S. Chakraborty, S. Roy, W.B.A. Karaa, S. Nath, N. Dey, “1-D Group Cellular Automata Based Image Encryption Technique,” in 2014 IEEE International Conference on Control, Instrumentation, Communication and Computational Technologies (ICCICCT), Kanyakumari, India, 521-526, 2014. https://doi.org/10.1109/ICCICCT.2014.6993017
8.  H.S. Jeong, K.C. Park, S.J. Cho, S.T. Kim, “Color medical image encryption using two-dimensional chaotic map and C-MLCA,” in 2018 10th International Conference on Ubiquitous and Future Networks (ICUFN), Prague, Czech Republic, 801-804, 2018. https://doi.org/10.1109/ ICUFN.2018.8437025
9. R.Enayatifar, H.J. Sadaei, A.H. Abdullah, M. Lee and I.F. Isnin, “A novel chaotic based image encryption using a hybrid model of deoxyribonucleic acid and cellular automata,” Opt. Laser Eng., 71(8), 33-41, 2015. https://doi.org/10.1016/j.optlaseng.2015.03.007
10. Y. Zhou, L. Bao, C.L.P. Chen, “A new 1D chaotic system for image encryption,” Signal Process., 97, 172-182, 2014. https://doi.org/ 10.1016/j.sigpro.2013.10.034
11.  J.V. Neumann, Theory of Self Reproducing Automata, University of Illinois, Urbana, 1966.
12. S. Wolfram, “Computation theory of cellular automata”, COMMUN MATH PHYS, 96(1), 15-57, 1984. https://doi.org/10.1201/9780429494093-4
13.  S.J. Cho, U.S. Choi, H.D. Kim, Y.H. Hwang, J.G. Kim and S.H. Heo, “New synthesis of one-dimensional 90/150 linear hybrid group cellular automata,” IEEE Trans. Comput-Aided Design Integr. Circuits Syst., 26(9), 1720–1724, 2007. https://doi.org/10.1109/TCAD.2007.895784
14. U.S. Choi, S.J. Cho, H.D. Kim, J.G. Kim, “Analysis of 90/150 CA corresponding to the power of irreducible polynomials,” J. Cell. Autom., 14(5-6), 417-433, 2019.
15. P.P. Chaudhuri, D.R. Chowdhury, S. Nandi and S. Chatterjee, Additive cellular automata, Theory and applications, vol. 1, Los Alamitos; California; IEEE Computer Society Press, 1997.
16. B. Hasselblatt, A. Katok, A First Course in Dynamics: With a Panorama of Recent Developments, Cambridge University Press, 2003.
17. G. Chen, Y. Mao and C.K. Chui, “A symmetric image encryption scheme based on 3D chaotic cat maps,” Chaos Solitons Fractals, 21(3), 749-761, 2004. https://doi.org/10.1016/j.chaos.2003.12.022
18. U.S. Choi, S.J. Cho, J.G. Kim, S.W. Kang, H.D. Kim, S.T. Kim, “Color Image Encryption Based on PC-MLCA and 3-D Chaotic Cat Map,” in 2019 IEEE 4th International Conference on Computer and Communication Systems (ICCCS), Singapore, 2019. http://doi.org/10.1109/ CCOMS.2019.8821691
19. X. Wang, Y. Zhao, H. Zhang, K. Guo, “A novel color image encryption scheme using alternate chaotic mapping structure,” Opt. Laser Eng., 82, 79-86, 2016. https://doi.org/10.1016/j.optlaseng.2015.12.006
20. X. Wu, H. Kan, J. Kurths, “A new color image encryption scheme based on DNA sequences and multiple improved 1D chaotic maps,” Appl. Soft Comput., 37, 24-39, 2015. https://doi.org/10.1016/j.asoc.2015.08.008
21.  L. Zhang, Z. Zhu, B. Yang, W. Liu, H. Zhu, M. Zou, “Cryptanalysis and improvement of an efficient and secure medical image protection scheme,” Math. Probl. Eng., 2015(2), 1-11, 2015. https://doi.org/10.1155/2015/913476

(Click Here)

(Click Here)