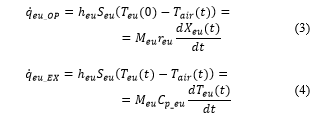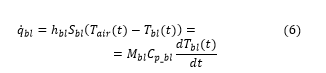1. Introduction

This paper is an extension of the work originally presented in 2019 Spring Simulation Conference (SpringSim), Tucson, Arizona, USA [1]. The paper presented the study of a safe and integrated transport system for blood and blood derivatives, employing the most advanced simulation and communication technologies. In the present extended version, the simulator of the box dynamic behavior has been improved by implementing a more detailed and more realistic thermal exchange model.

The paper addresses the topic of healthcare safety [2-4], focusing on the problem of blood bags transport. The transportation of biologic material [5,6] presents risks related to the exceeding of deterioration temperature thresholds therefore, other than designing a transport container provided with a long range cooling system, it is necessary to manage the temperature control in different ambient conditions and to monitor the material status during travel time [7]; this aspect highlights the importance of data exchange with a central unit (hospital or blood bank), which is in charge of providing real-time logistic coordinates (i.e. the nearest possible point of blood collection) to prevent deterioration.

The usual procedures applied to the transport of biologic material provide the samples collection from distributed locations and their subsequent delivery to a laboratory for the analyses. In recent years, the increased costs and the complexity of clinical analysis equipment, has directed the management choices towards the concentration of the most important activities (e.g. analysis) in large centralized laboratories, from which depend a great number of smaller collection points. Only large and highly automated laboratories can reach the required scale economies to process a large number of samples with satisfying economical profitability.

Since the distance between central labs and collection points can be significant and the traffic situation can dramatically increase transport time [8-10], the need to extend and control the autonomy of the cold storage becomes a central issue. Moreover, another critical aspect regards the continuous increase of blood banks centralization in order to cover larger areas, which involves longer travel time; thus, the issue arises of ensuring protection, traceability and continuous monitoring of blood bags during their travel.

The transport box ensures the cooling effect to the biologic material by exploiting an array of eutectic elements opportunely disposed in a separate compartment. From the latter, on-off blowers, activated by measured temperature signal, deliver a flow rate of cold air to the blood bags compartment, withdrawing heat to keep temperature within the safety range. The box envisages a cloud connection with a central server unit, on which is uploaded the dynamic simulator main object of this article, able to calculate the box temperature and thermal autonomy in function of time. On the same central server, a logistic model receives in real time the box geo-localization data [11-13] and gives as output the coordinates of the nearest center for safe blood storage in case of box thermal autonomy exhaustion.

The objectives of this paper are:

1) Implementing a more realistic thermal exchange model for the container, including air-blood and air-eutectic thermal exchange correlations;

2) Evaluating the dynamic characteristics of the container, by building diagrams which show the time variation of temperature for air, blood and eutectic and liquid mass fraction variation with time for eutectic;

3) Assessing the simulated performance of the container in terms of duration of the cooling effect and number of blowers interventions in different environmental conditions.

2. Features of the Blood Transport System

The main scope of the proposed integrated transport system is enabling healthcare operators to monitor, track and certify the quality of each transported biological good (plasma, blood, platelets…), by a complete traceability of the transport.

The integrated transport system consists in the active interaction between thermally insulated intelligent transport containers for blood products storage and a central computer unit dedicated to recording the whole history of the transport variables, other than processing the data received from the smart boxes (e.g. internal temperature and spatial position) to predict the exhaustion time and the nearest point of collection where the material can be safely stored. The transport boxes in motion dialogue with the central unit by cloud connection.

2.1.  Smart Box Constructional Features

The smart container is constantly cloud-connected to a central server in order to monitor, record and signal, in real time, possible failures and alerts for the main operational variables, as:

• Box inner temperature;
• Ambient temperature;
• Relative humidity;
• Geo-localization (GPS, GSM, GLONASS, GALILEO);
• Speed of traveling;
• Accelerations;
• Tilting of the box;
• Physical integrity of the device;
• Date, time, minute
• Name of the responsible for each operation (switching on, loading, shipping, delivering, unloading, switching off, inspection).

In particular, regarding the latter function, each operator will be equipped with a card by means of which he can interact with the box; according to the field of expertise of the operator, he will be allowed to all or just certain actions on the box (e.g., a paramedic in charge for the transport will not be allowed to open the box or change the temperature set-point, whereas a medicine doctor will).

The box is designed to keep the inner temperature within a safety range, defined by the user according to the type of product and the external conditions. The cooling effect must contrast the thermal flow which enters the box from the environment and is ensured by eutectic plates confined in a separate compartment from the blood storage area. The eutectic plates release their thermal content when required, thanks to the “smart wall” which separates the eutectic plates zone from the blood products storage zone, providing the ventilation through correctly sized blowers activated by the signals from the sensors mounted inside the box. A scheme of the box components is shown in Figure 1.

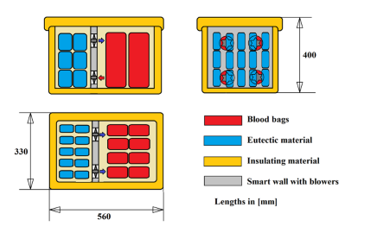Figure 1: Schematic view of the Smart Box.

The box cooling system is not intended to cool down the biologic material starting from ambient temperature; therefore, the transported blood products need to be loaded at the desired transport temperature. The box is designed to keep the temperature range for no more than 5 hours.

The box functions are settable through a PLC equipped with LCD monitor. Operators interacting with the smart box are identified by a magnetic card which, basing on the permissions released to each person, permits to enable or disable the various box functions (opening, closing, change of settings …). The box can also be managed through an online portal from which the user can monitor the status and interact with the boxes in travel.

2.2.  Data Exchange

The above listed physical quantities are measured by means of sensors installed in the Smart Box, sampled with a frequency of 5 Hz. Such quantities are sent to a central server. According to the availability of GSM network, the collected data are stored in a local memory from which they are sent to the server. If available, the box can exploit a dedicated Wi-Fi router in place of the GSM.

In Figure 2 is shown the scheme of the network connections for data exchange.

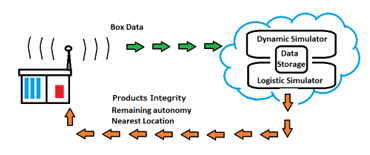Figure 2: Box connection system.

3. Matlab Simulink Model

The dynamic modelling of a process has the purpose to reproduce, using differential equations, the variation with time of the system main parameters [14-17]. The variables observed by the smart box blood transport model are the blood temperature and the eutectic liquid mass fraction, which are influential parameters for the blood status and for the box autonomy.

Compared to the simulation model described in [1], the system of differential equations solved by the simulator here presented has been improved by introducing the thermal exchange equations between the air contained in the box and the stored blood and eutectic material. The algorithm for switching on-off the blowers has been set to have as controlling variable the temperature of the air contained in the box, measured by thermocouples.

3.1.  Air Thermal Balance

Equation 1 describes the thermal balance of the air contained within the smart box, in contact with the blood, the eutectic, the confinement walls and the electric blowers for its circulation. The temperature of the air mass varies in function of the thermal flow contributions to which it is subjected.

In Equation 1:

 is the temperature of the air contained within the box, of mass , having specific heat capacity , the latter calculated in function of temperature by using the Langen coefficients.

 and  represent the thermal flows exchanged between the air and, respectively, the blocks of eutectic material and the blood bags.

 represents the total external flow heating up the material in the box, which is the sum of the thermal flow entering from the insulated walls ( ) and the electric power of the blowers ( ), as shown in Equation 2.

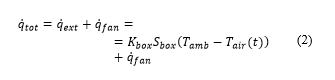 and  are respectively the transmittance and external surface area of the box walls,  is the external ambient temperature.

is the power of the four blowers (fans) installed in the smart wall to ensure the air circulation when required; since the air loop is closed, all the fans electric power (4 W) is injected into the air stream and contributes to increase its temperature when fans are active.

In Figure 3 is represented the scheme of the thermal balance for the air, implemented with Simulink blocks.

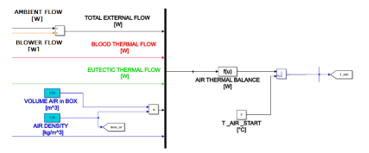Figure 3: Simulink block scheme for thermal balance of air contained in the box.

3.2.  Eutectic Thermal Balance

Equation 3 and Equation 4 reproduce the thermal balance of the eutectic material; the first equation is employed in normal operation, when the eutectic has not yet molten down completely and represents the eutectic behavior during meltdown, describing the liquid mass fraction time variation ( ). Such parameter increases from 0 to 1 while temperature remains at the equilibrium value of – 2°C; the second equation considers the temperature increase of the molten eutectic ( ) subjected to the incoming thermal flow.

In these equations:

 is the eutectic mass, set to 1 kg;

 is the latent meltdown heat of the eutectic, set to 265 070 J/kg;

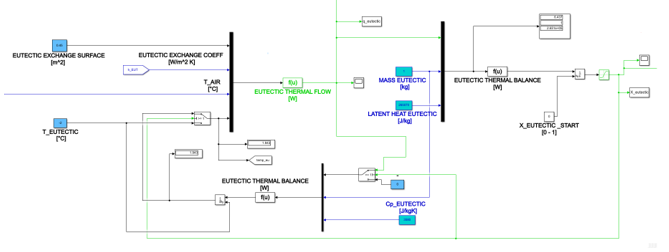Figure 4: Simulink block scheme for thermal balance of melting/molten eutectic material.

 is the specific heat capacity of the liquid eutectic, set to 3560 J/kg K;

 is the thermal exchange coefficient between air and eutectic material blocks, the latter having a total heat exchange surface equal to .

 is the liquid mass fraction of the eutectic, defined in Equation 5:

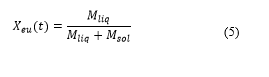 and  are the masses of liquid and solid eutectic during transport time.

Figure 4 shows the block scheme implemented in Simulink for the eutectic balance.

3.3.  Blood Thermal Balance

Equation 6 represents the thermal balance of the blood contained in the storage vane.

In Equation 6:

 is the blood temperature; the correct range for transport is between 4°C and 8°C.

 is the mass of the stored blood, equal to 7 kg;

 is the blood specific heat capacity, equal to 3900 J/kg K;

 is the thermal exchange coefficient between air and blood bags, the latter having a total heat exchange surface equal to .

Figure 5 shows the block scheme implemented in Simulink for the blood balance.

3.4.  Heat Exchange Coefficients

To compute the heat exchange dynamics between the air contained in the box and the blood and eutectic materials, it was necessary to carry out a research regarding the thermal exchange

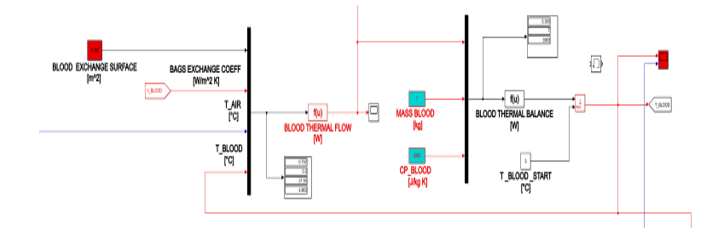Figure 5: Simulink block scheme for thermal balance for thermal balance of blood material.

coefficients in confined narrow channels. [18-21]. Since the heat exchange within the box may occur both in presence of forced air circulation (blowers on) and in calm air (blowers off), two heat exchange correlations have been individuated and applied to the box geometric and thermo-fluid dynamical characteristics. The correlations employed, based on Nusselt number, are presented respectively in Equation 7 for the forced circulation case and in Equation 8 for the natural circulation case:

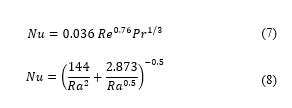 being the circulating flow Reynolds number, calculated basing on the mass flow rate of the blowers, equal to 0.018 kg/s;  being the air Prandtl number and  the Rayleigh number, for natural convection correlations.

These two correlations have been implemented in Simulink blocks both for the blood compartment and for the eutectic compartment, determining the heat exchange coefficients in natural and forced convection; the switching between the two conditions occurs in function of the on-off signal provided to the blowers so that, when the latter are switched on, the heat exchange coefficient used by thermal balance equations is the one obtained by Equation 7; otherwise, the one obtained by Equation 8.

3.5.  Temperature Control Modelling

Figure 6 illustrates the scheme, implemented in Matlab-Simulink, of the box temperature control system [22], finalized to keep the blood compartment in the safe temperature range.

The controlled variable is the box internal air temperature, which is detected by sensors and sent to the control system.

The controlling variable is the on-off signal to the blowers, managed according to the following logics:

Blowers switch-off as T_air(t) < Tmin;

Blowers switch-on as T_air(t) > Tmax;

Keep blowers status (on or off) as temperature remains in the desired range: Tmin < Tair(t) < Tmax.

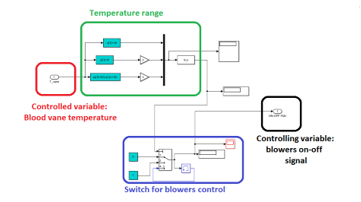Figure 6: Matlab-Simulink block scheme of the blowers control system.

The control algorithm has been implemented by Matlab-Simulink logic blocks: the time varying compartment temperature is compared to the set-point values Tmin and Tmax, providing 0 or 1 signals which are sent to a multi-port switch that provides the on-off signal to the blowers respecting the above-mentioned logics.

4. Results of the Simulations

The smart box simulator improved with air-material thermal exchange correlations has been tested to assess its behavior. The main difference between the present model and the one proposed in [1] stands in the explicit modeling of the air behavior inside the compartments, operating as a heat vector during transport time.

The controlling variable selected to provide a feedback to the blowers on-off signal is the internal air temperature, while in [1] the blood temperature had been chosen. The control algorithm has been set in order to switch on the circulation blowers as air temperature approaches 8°C and to switch them off as it reaches 4°C. It has to be noticed that the blood loses its properties as its temperature overcomes 8°C for a significant time period.

Regarding the environmental conditions of the test, two different periods of the year have been chosen, namely May and August, characterized by external air temperatures of respectively 21°C and 27°C.

The model outputs monitored during simulations are:

• The blood temperature, ;
• The temperature of air contained in the box, ;
• The liquid mass fraction of the eutectic , in the [0 – 1] range;
• The eutectic temperature ; as soon as reaches 1, the eutectic latent heat useful for cooling is exhausted; however, some cooling is still ensured by the eutectic sensible heat, while increasing its temperature;
• The number of blowers on-off cycles;
• The time to cooling effect exhaustion.

The following paragraphs illustrate the simulations results; the tests have been performed setting the input parameters listed in the 3rd chapter and the simulator running time has been stopped after about 7 hours (25 000 s).

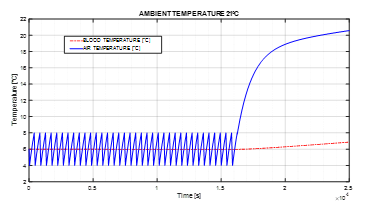Figure 7: Blood and air temperatures in function of time (simulation for the month of May).

4.1.  Results for the Month of May

Figure 7 shows the diagram of blood and air temperatures in function of time.

The blood remains in the correct temperature range for all the simulated time period, reaching a temperature of 6.9°C at the instant of simulation stop (25 000 s, about 7 hours). The circulation blowers are switched on for 36 times, as verifiable from the air temperature curve. As soon as the eutectic reaches exhaustion, internal air temperature increases tending to the ambient temperature value.

Figure 8 shows the time diagram for eutectic temperature and liquid mass fraction.

The eutectic effect ends at 16250 s (4.51 h), after which its temperature increases from the equilibrium value of – 2°C and tends, after a transient dictated by the material thermal capacity, to reach equilibrium with the external temperature.

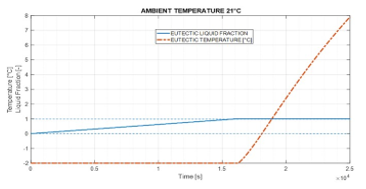Figure 8: Eutectic liquid mass fraction and temperature in function of time (simulation for the month of May).

With respect to the results obtained in [1], the increase in the number of blowers on-off interventions appears remarkable. This effect is due to the inclusion of the air-materials thermal exchange effect: the mass of air contained in the box is limited (0.03 kg) and its specific heat is low compared to liquid or solid substances; therefore, air temperature rises and falls result very fast with respect to blood, which keeps almost constant temperature for all the simulated period. Having chosen the internal air temperature as control variable for the blower signal, the latter is forced to follow the air behavior, which increases dramatically the number of on-off switches.

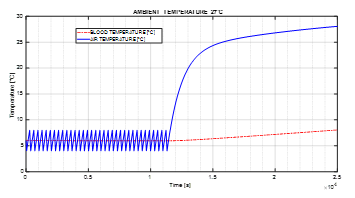Figure 9: Blood and air temperatures in function of time (simulation for the month of August).

4.2.  Results for the Month of August

Figure 9 reports the diagram of blood and air temperatures in function of time.

In the hot month of August, the blood temperature keeps below 8°C (blood deterioration threshold) for 24 701 s (6.86 h), and the blowers are activated for 34 times. As soon as the eutectic reaches exhaustion, internal air temperature increases tending to 27°C.

In figure 10 is shown the eutectic temperature and liquid mass fraction diagram in function of time. The eutectic cooling effect is exhausted after 11330 s (3.15 h).

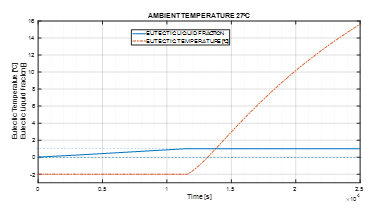Figure 10: Eutectic liquid mass fraction and temperature in function of time (simulation for the month of August).

Table 1 reports a synthesis of the simulations parameters and results for the two periods considered.

Table 1: Synoptic table of the simulated parameters.

Parameter	[Units]	May	August
Ambient temperature	[°C]	21	27
Stored blood mass	[kg]	7	7
Initial blood temperature	[°C]	5	5
Eutectic mass	[kg]	1	1
Eutectic equilibrium temperature	[°C]	-2	-2
Blowers flow rate	[kg/s]	0.018	0.018
Eutectic effect exhaustion time	[h]	4.51	3.15
Threshold temperature attainment time	[h]	> 7	6.86
Blowers interventions	#	36	34

5. Conclusions

Blood products transport, topic of clear interest for the healthcare sector, has been addressed in the original article [1], which proposed a thermally insulated portable box equipped with a ventilation cooling system and an informatics support system monitoring the transport data (e.g. time remaining before the exhaustion of cooling effect, the logistic data of the nearest blood collection point…) through a central control unit. The present extended paper addresses the improvement of the dynamic Matlab-Simulink simulator for said blood transportation system.

The Matlab-Simulink model is supposed to help the correct sizing of the box in a design phase (walls insulation, mass ratio between eutectic and blood, blowers air flow rate, …) and to operate as an online simulator for calculating the box main variables (blood temperature and remaining autonomy) during transport.

The improvement on the Matlab-Simulink model, which regarded the introduction of correlations for considering the thermal exchanges between air and transported materials, is expected to provide results more in accordance with real operation.

The test simulations have been carried out for two periods of the year, namely May (21°C) and August (27°C). In general, the results of the improved model showed a similar cooling effect exhaustion time compared to the original model in [1]. The main difference stands in the number of interventions of the controlled blowers, which resulted about 7 times more frequent than what predicted by the original model. This effect results from the inclusion of the internal air heat exchange correlations and from the choice of using air temperature as the controlling variable for the blowers activation; being the small amount of air trapped within the box very fast in increasing and decreasing temperature, it results clear that the blowers will be called in operation frequently.

Future development of the technology described in this paper is the construction and testing of a smart-box for blood products transport, in order to assess its real performance when interacting with the actual environment. Also, more effort will be addressed to the development of the inter-connection informatics system, together with the implementation of an efficient geo-localization and optimization algorithm for the indication of the nearby healthcare facilities.

Conflict of Interest

The authors declare no conflict of interest.

Acknowledgment

Authors would like to acknowledge Genoa University.

1. Damiani L., Revetria R., Arecco S., Simulation model of the control system of portable boxes for blood bags transport, SpringSim-MSM 2019, April 29-May 2, Tucson, AZ, USA. DOI: 10.22360/springsim.2019.msm.001.
2. Damiani, L., Revetria R., Mzoughi K., Giribone P., A Hybrid Simulation Model for Evaluating Risk Related to Complex Plants in Hospitals, Proceedings of the World Congress on Engineering and Computer Science 2016 Vol II WCECS 2016, October 19-21, 2016, San Francisco, USA.
3. Damiani, L., Giribone P., Mzoughi K., Revetria R., A Hybrid Simulation Model for Hospital Complex Plants Risk Evaluation, 2017, Engineering Letters, 25.2.
4. Patrone, C., Cassettari L., Damiani L., Mosca R., Revetria R., Optimization of Lean Surgical Route through POCT Acquisition, IAENG Conference IMECS 2017, Hong Kong, 15 – 17 March 2017.
5. Ruiz-García, L., et al.: Monitoring the intermodal, refrigerated transport of fruit using sensor networks. Spanish Journal of Agricultural Researh 5(2), 142–156 (2007).
6. Gil-Castiñeira, F., Chaves-Diézquez, D., González Castaño, F.J.: Integration of nomadic devices with automotive user interfaces. IEEE Transactions on Consumer Electronics 55(1), 34–41 (2009).
7. Castro, M., A. J. Jara, A. F. G. Skarmeta, Analysis of the Future Internet of Things Capabilities for Continuous Temperature Monitoring of Blood Bags in Terrestrial Logistic Systems, in: Lee G., Howard D., Ślęzak D. (eds) Convergence and Hybrid Information Technology. ICHIT 2011. Lecture Notes in Computer Science, vol. 6935, Springer, Berlin, Heidelberg.
8. Gibson, J.G., T. Sack, R.D. Evans, W.C. Peacock, The Effect of Varying Temperatures on the Post Transfusion Survival of Whole Blood During Depot Storage and after Transportation by Land and Air, The Journal of clinical investigation, 1947, Vol.26(4), pp.747-755.
9. Or, I., W.P. Pierskalla, A Transportation Location-Allocation Model for Regional Blood Banking, A I I E Transactions, 11 (2), 1979.
10. Fakhr, A.A., Bikmoradi A., Zandiyh M., Mozafari H., The assessment standards related to blood transportation, storage, preparation, and administration in operating rooms of Hamedan educational treatment centers, Scientific Journal of Iranian Blood Transfusion Organization, 2012, Vol. 9 Issue 1, pp. 63-71.
11. Ngai, E.W.T., Cheng, T.C.E., Au, S., Lay, K.: Mobile commerce integrated with RFID technology in a container depot. Decision Support Systems 55(1), 62–76 (2007).
12. Atzori, L., Iera, A., Morabito, G.: The Internet of Things: A survey. Computer Networks 54, 2787–2805 (2010).
13. Guinard, D., et al.: Interacting with the SOA-Based Internet of Things: Discovery, Query, Selection, and On-Demand Provisioning of Web Services. IEEE Transactions on Services Computing 3(3), 223–235 (2010).
14. Damiani, L., Trucco, A. An experimental data based correction method of biomass gasification equilibrium modeling, Journal of Solar Energy Engineering, 2010, 132(3).
15. Damiani, L., Giribone P., Revetria R., Pini Prato A., A passive decay heat removal system for the lead cooled fast reactor demonstrator “Alfred”, Progress in Nuclear Energy 83 (2015) 294-304.
16. Damiani, L., Pini Prato A., Simulation of a Power Regulation System for Steam Power Plants, Energy Procedia, 45 (2014) pp. 1185-1194.
17. Dellachà, J., Damiani L., Repetto M., Pini Prato A., Dynamic Model for the Energetic Optimization of Turbocompound Hybrid Powertrains, Energy Procedia 45 ( 2014 ) 1047 – 1056.
18. Kotcioglu I., Ayhan T., Olgun H., Ayhan B., Heat Transfer and Flow Structure in a Rectangular Channel With Wing-Type Vortex Generator, Tr. J. of Engineering and Environmental Science 22 (1998) , pp. 185 – 195.
19. Rybinski W., Mikelewicz J., Analytical solutions of heat transfer for laminar flow in rectangular channels, Archives of Thermodynamics, Vol. 35(2014), No. 4, pp. 29–42 DOI: 10.2478/aoter-2014-0031.
20. Forrest E.C., Hu L.W., Buongiorno J., McKrell T.J., 2016, Convective Heat Transfer in a High Aspect Ratio Mini-Channel Heated on One Side, Journal of Heat Transfer, 138(2): 021704.
21. Tanda G., Natural convection heat transfer in vertical channels with and without transverse square ribs, 1997, Int. J. Heat Mass Transfer, Vol. 40, No. 9, pp. 2173-2185.
22. Damiani, L., Giribone P., Guizzi G., Revetria R., Romano E., Different approaches for studying interruptible industrial processes: Application of two different simulation techniques, Handbook of Research on Computational Simulation and Modeling in Engineering, 2015.

(Click Here)

(Click Here)