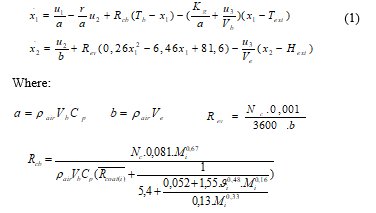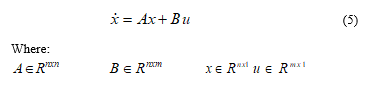1. Introduction

The poultry house climate is defined as the principal part that can straightforwardly influence the efficiency and comfort of the raising birds. Notwithstanding, the control of the housed livestock building remains a confounded errand because of the nonlinear behavior of psychrometric mechanisms required on both physiological and psychological components.

In most cases, the poultry farming is mainly affected by the outside condition (external relative humidity and temperature) and by the control of the actuators of the system (PAD cooling, heating, and ventilation system) [1]. Recently, the agricultural sector has extended altogether regarding control and optimization strategies for the primary parameters influencing good livestock management.

The hygro-thermal parameters are the most critical environmental variable on the poultry as announced in [2], [3]. Additionally, it has mutually been shown that the relative humidity and temperature affect intently the animal’s improvement in Morocco because of the dominating weather and the country’s location.

In this regard, we target our works to extend the ongoing studies by designing a suitable control strategy that is created depending on the mathematical model of broiler houses under cold conditions.

Over the most recent couple of years, the late research investigation demonstrates a tendency to the utilization of progressively different advanced procedures for control systems and simulation for a livestock building.

For the most part, it exists two types of control techniques, traditional techniques, and modern techniques. In such manner, numerous researches on livestock building concerning climate-controlling have been suggested in the literature, for example, nonlinear robust control for pig house [4], nonlinear adaptive control for animals house [5], predictive control for temperature and humidity in a normally ventilated structure [6], SMC (Sliding Mode Control) to control both of interior temperature and relative humidity in an evaporative cooling system [7].

Others studies related to the optimization control have been developed in the livestock building, for instance, the application of the ant colony optimization (ACO) for control broiler house under hot climates [8] and the utilization of the particle swarm optimization (PSO) in the managing of the thermal requirement of the poultry house.

In other hands, the fuzzy logic controller has been well tested in a greenhouse and poultry house [9], authors are reasoned that is fuzzy controller was able to give a superior efficiency in the stability. Other researchers [10] and [11] have linked a PID with fuzzy controllers to control the temperature indoors poultry house, they had concluded that the fuzzy-PID structure has excellent performance over a PID controller as far as settling time and steady-state error. A comparison between fuzzy and on/ off controllers have been analyzed in [12] to test and keep up the ambient parameters inside a model poultry house. Accordingly, all these advanced control systems have demonstrated their similarity to be used on control structure applications for poultry houses.

In this paper, the present work describes an extension of the original work reported in Proceedings of the International Conference on Automation and Computing [13].

The contributions of this article are portrayed as looks for: (1) to design a state-PID feedback controller to guarantee nominal stability and to regulate the hygro-thermal parameter of the system to a given set point value. (2) Implement the proposed controller in a real poultry house prototype system.

 Hence, the inspiration for the state-PID feedback controller in this manuscript originates from some papers dealing with a wide variety of systems such as the SISO and MIMO systems [14] ,[15],[16].

The control configuration begins with the deduction of the linearized hygro-thermal model of the poultry process proposed in [17], at that point develops the state-PID feedback controller utilizing the eigenvalue assignment algorithm.

The remainder of the paper is formulated as follows:  the primary segment exhibits quickly the hygro-thermal model of the poultry process. The second section describes the methodology of the state-PID feedback controller (SFCPID). Finally, some simulation results and remarks for stabilization and disturbance rejection are given to show the effectiveness of the proposed controller.

2. Mathematical model

2.1.    Hygro-thermal model

Considering the mathematical modeling of the previous work detailed in [17] and the proposed studies on climate modeling inside livestock buildings [6] [18], the hygro-thermal model administered the poultry house is:

The state space form of the model (1) is represented in equation (2). The study is conducted with the cold operations where the controller input related to the PAD cooling system isn’t working (E_ev = U₂ = 0).

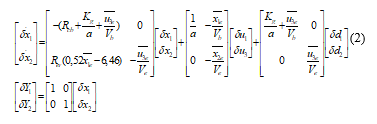Where x are states variables associated with the internal relative humidity and temperature, u₁ and u₂ are the input controller associated with the heating system and the ventilation system, d are external disturbances.

The linearized model (2) can be simplified and represented to as a state space structure yielded (3):

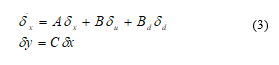C is the output matrix, B and B_d are the input matrix and A is the state matrix.

2.2.  Local Stability

We recommended concentrating to study the global stability of the general system (nonlinear) from its linearized tangent.

Let us consider the nonlinear system expressed as:

After calculating, we get:

If the case of , especially when the livestock building system work just with the heating system ( ).

The eigenvalues of the matrix are:

It is clear that the process is locally on the cutoff of the stability, and requires stabilization with an appropriate controller.

3. State-PID feedback controller design

In this section, state feedback and PID controllers are designed for the linear state space proposed model of the broiler house process.

3.1. State feedback controller

Let’s consider the LTI system which having the following form:

Where:

The linear system under consideration must to be totally controllable, the controllability matrix must have a full rank-n [19][20] and can be communicated as

The pair (A, B) is controllable.

Figure 1 illustrates the basic feedback controller of the poultry house.

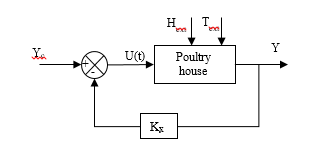Figure 1: State feedback controlled poultry house system.

Where Y_c, U, Y and K_x  are the command signal, the control law, the output of the plant and the feedback controller, respectively.

The control law can be composed on the structure:

      The objective of this controller is to stabilize the system by the constant feedback control that imposes to place the poles at desired characteristic behavior for the states.

      Using the feedback control law (7), the closed-loop characteristic polynomial system is given by:

The structure issue is to determine the feedback gain matrix K_x such that the closed-loop poles { } of the system (8) are appointed at the desired values.

The methodology proposed to this problem is accomplished by using the pole placement algorithm.

The assignment placement algorithm concedes finding the matrix K_x, such as the closed-loop, system is stable. Both the desired closed loop poles and the eigenvector relating.

The following steps present the algorithm used for the assurance of the gain components of matrix K_x is: [21]

3.2.    State-PID feedback controller

In this area, we introduce the proposed strategy control; we use in conjunction the state feedback and the PID controller.

The Proportional Integrator Derivative structure is one of the most controller broadly utilized in the industry, covering more than 90% of the industrial need in control. This predominance is because of its simplicity to implement it in a large plant does not require detailed knowledge. The control block scheme is shown in figure 2.

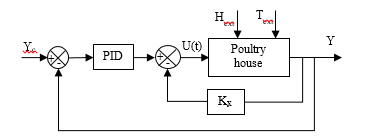Figure 2: State-PID feedback proposed controller.

The control law u of the state-PID feedback proposed controller is :

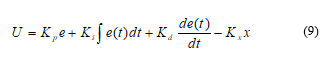Where  are the planned gain matrices to achieve a desired closed-loop system.

In summary, the problem described is resolved for a pole placement method consisting of three separated steps as mentioned in Guo et al [22].

The pole placement by state-P feedback is directed first prompting an intermediate system. Furthermore,  state-I feedback is executed; another transitional system resulted. At last, the closed-loop system with the desired characteristic polynomial is acknowledged by state-D feedback joined as the final plan configuration.

The components of state-PID controller gain matrices for the PID structure can be obtained using the transformation into Frobenius canonical form detailed in [23],[24] and the equations mentioned in [15].

4. Results and discussions

In this analysis, we suggest regulating the internal temperature T_int and relative humidity H_int under cold climates, for that we design the state-PID feedback controller to get synchronization to deal with both ventilation and heating systems.

To affirm the performance of the proposed state-PID feedback controller, several comparative illustrative simulations are delineated.

4.1.    Case 1: simulation study

The industrial poultry house system was equipped with controller natural ventilation, heating and PAD cooling system, the livestock building dimensions were 12,4m x 120m x 3,85m.

The real plant data have been saved for the entire period for the chickens raising of [20-21] days under the climates of the Mediterranean region (Rabat area, Morocco). (Figure 3)

Figure 3: Poultry house system used in the case study.

Table 1 presents the numerical estimations of the distinct criterions used in the simulation of the proposed controller.

Table 1: Input specifications used in the hygro-thermal model

Specifications	Values	Specifications	Values
	1,2kg/m3		41°C
	1006J/kg.K		24000
	3033m3		3033m3
	0,905kg		0,2m/s
	0,2 m2.K/W		3126W/°C

Design of state feedback controller

The conventional (SFC) design technique begins with the determination of the desired eigenvalues from the given specifications of the controller K_x : ,  of an order of multiplicity respectively (n) and (n-1).

The basis of controllability is verified of the system (2) after including the different parameters:

Rank (C) =2

The specifications considered for the poultry house system are selected primarily on diminishing the steady-state error and the settling time.

After choosing the desired pole and applying the assignment eigenvalues algorithm, we find:

The input control of the system is :

Design of state-PID feedback controller

The feedback gain matrix is computed as:

The PID gain matrices is obtained as :

Stability analysis

The comparison of the closed loop response of the hygro-thermal parameters concerning the desired values of poultry house system with conventional state feedback, state-PI feedback and state-PID feedback controller using the package Simulink of MATLAB are demonstrated in figure 4 and 5.

For numerical simulation, the desired relative humidity and internal temperature have been fixed at 66% and 26°C.

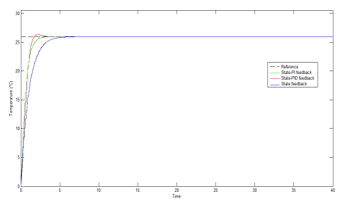Figure 4: Temperature response generated by the different controller.

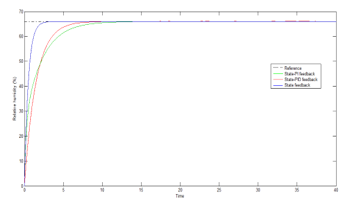Figure 5: Humidity response supplied by the different controller

The state-PID feedback controller configuration performed wells; however, the state feedback controller performs moderately.

It can be clearly seen in figure 4 and 5 that there are different responses in the transient state performance. The numerical values of these performances of the closed loops are tabulated in table 2 for comparison.

Table 2: Numerical values of standard performance indices.

	Performances indices	SFC	SFCPI	SFCPID
Temperature	Rise time (s)	2,42	1,38	1,21
	Settling time (s)	3,128	1,66	1,49
	Overshoot (%)	0	0	1,54
Relative humidity (%)	Rise time (s)	1,12	4,14	3,76
	Settling time (s)	1,31	5,62	4,37

From table 2, it appears that the state feedback controller gives poor results compared to that of state-PI and PID feedback controller in control of temperature. Other hands, the SFCPI gives a slow response compared to that of state-PID feedback state and a state feedback controller. Furthermore, the SFCPID affords the littlest value of rise time evaluated at 1,21s and the smallest value of settling time estimated at 1,49s.

It tends to be additionally observed that the performances indicated by the proposed controller are closely at their best values. The transient responses of states are plotted in figure 6 and 7.

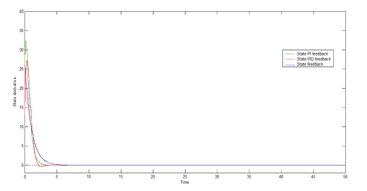Figure 6: Response of the state derivative of the internal temperature.

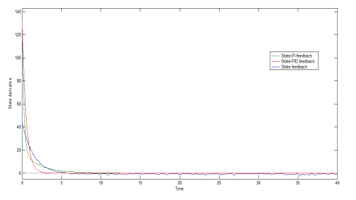Figure 7: Response of the state derivative of the relative humidity.

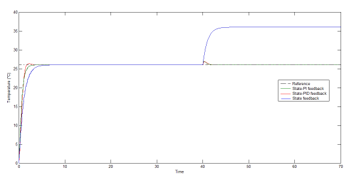Figure 8: Temperature response simulated under disturbance with the different controller.

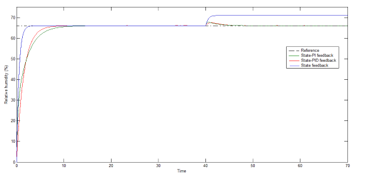Figure 9: Relative humidity response simulated under disturbance with the different controller.

Figure 10: Experimental poultry house prototype.

From figures 6 and 7, it can be noticed that the derivative of the internal temperature accelerates rapidly within the state-PID feedback controller compared to that of SFCPI and that of state feedback. Also, it can be observed that the derivative response converges to zero after a short duration and this proves that the internal temperature and relative humidity have been well stabilized.

Disturbance rejection

The temperature and humidity response under the external disturbance with the three controllers are displayed in figures 8 and 9.

From figures 8 and 9, it very well may be obviously observed that with our proposed controller that the system reactions quicker, and recuperates totally from the external disturbance without any residue errors. This is because of a derivative and integral parameters acting as an error corrector.

Furthermore, it tends to be seen that the planned state-PID feedback controller maintains the internal temperature and relative humidity within a short time of 7 seconds after applying a disturbance; however, the conventional state feedback controller isn’t able to reduce or eliminate the external disturbance in both of temperature and relative humidity response.

4.2.    Case 2: Experimental poultry house prototype

The poultry house prototype has two main actuators, namely, the electric heater and the fans systems. Other subsystems contain lighting and evaporative cooling systems are also installed. The system program includes the main algorithm unit for all systems in the broiler house. In addition, the experimental data is transmitted to the computer device using a micro controller. The real data is monitored with the LabVIEW software; the users can control the important operations and can to be informed of the various changes for the system. (See figure 10)

The internal temperature is measured using LM35 and the relative humidity is acquired via HIH4030 sensor. The variable input of heating and ventilation system are fitted with a thyristor driver circuit in order to produce a varying voltage for running the fans and the heater at different level speed and stage. The change in applied voltages is legitimately relative to the airflow speed and heating rate.

The three controllers are implemented for the poultry house prototype and experimental results of the temperature and relative humidity response are represented in figures 11 and 12.

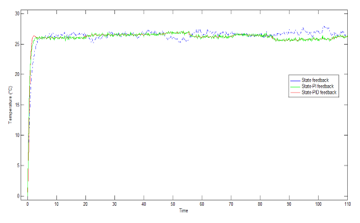Figure 11: Internal temperature response provided with the different controller.

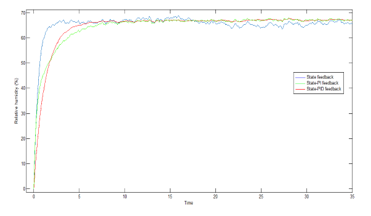Figure 12: Relative humidity response generated with the different controller.

The implementation of the different controller to the poultry house prototype control system show the better quality of using SFCPID in the regulation of the system. The results obtained with the state-PID feedback controller provide a better response for relative humidity and temperature response with a very smooth variation in tracking the desired set points.

5. Conclusions

In this article, we have proposed and designed a state-PID feedback controller for stabilizing the relative humidity and temperature indoor the broiler house process during the colds conditions.

Numerical examples are tested to confirm the effectiveness of the proposed design controller to stabilize the system. On the other, we have considered the existence of disturbance simulated as the external perturbations getting from the outside climate. The results of simulations show that the proposed methodology was proficient regarding dynamic performance, for example, a decrease of settling time and rise time. Moreover, the SFCPID was capable of tracking the desired set point with a rapid rate of convergence. Thus, the proposed controller has proven its performance through the simulations under disturbance and the comparative study conducted between the state feedback and state-PI feedback technique and the state-PID feedback controller.

In addition, the proposed controller is implemented for the real experimental poultry house prototype. It is concluded that the proposed state-PID feedback controller affords excellent performance than the state-PI feedback and state feedback controller in terms of following the set points parameters.

Finally, it is pointed out that the proposed control methodology of the poultry house accentuates the regulation of the system and the optimal parameters.

Conflict of Interest

The authors declare no conflict of interest.

Acknowledgment

This work was supported by the National Center for Scientific and Technical Research (CNRST) within the context of the Research Excellence Awards program.

1.  S. Yahav, A. Straschnow, D. Luger, D. Shinder, J. Tanny, and S. Cohen, “Ventilation, sensible heat loss, broiler energy, and water balance under harsh environmental conditions,” Poult. Sci., vol. 83, no. 2, pp. 253–258, 2004.
2.  N. J. Daghir, Ed., Poultry production in hot climates, 2nd ed. Wallingford: CABI, 2008.
3.  T. Banhazi et al., “Issues related to livestock housing under hot climatic conditions including the animals’ response to high temperatures,” Anim. Hous. Hot Clim., p. 4, 2007.
4.  A. G. Soldatos, K. G. Arvanitis, P. I. Daskalov, G. D. Pasgianos, and N. A. Sigrimis, “Nonlinear robust temperature–humidity control in livestock buildings,” Comput. Electron. Agric., vol. 49, no. 3, pp. 357–376, Dec. 2005.
5.  P. I. Daskalov, K. G. Arvanitis, G. D. Pasgianos, and N. A. Sigrimis, “Non-linear Adaptive Temperature and Humidity Control in Animal Buildings,” Biosyst. Eng., vol. 93, no. 1, pp. 1–24, Jan. 2006.
6.  P. I. Daskalov, “Prediction of temperature and humidity in a naturally ventilated pig building,” J. Agric. Eng. Res., vol. 68, no. 4, pp. 329–339, 1997.
7.  K. Senawong, S. Winitchai, and T. Radpukdee, “Humidity and temperature control in an evaporative cooling system of a poultry house,” Eng. Appl. Sci. Res., vol. 39, no. 1, pp. 95–111, 2012.
8.  I. Lahlouh, A. El Akkary, and N. Sefiani, “PID/Multi-Loop Control Strategy for Poultry House System Using Multi-Objective Ant Colony Optimization,” Int. Rev. Autom. Control IREACO, vol. 11, no. 5, p. 273, Sep. 2018.
9.  K. Chao, R. S. Gates, and N. Sigrimis, “Fuzzy logic controller design for staged heating and ventilating systems,” Trans. ASAE, vol. 43, no. 6, p. 1885, 2000.
10.  D. O. Aborisade and O. Stephen, “Poultry house temperature control using Fuzzy-PID controller,” IJETT Chennai, vol. 11, no. 6, pp. 310–314, 2014.
11.  R.Manoj Manjunath and S.Janaki Raman, “Fuzzy adaptive PID for Flow Control System based on OPC.” IJCA Special Issue on “Computational Science-New Dimensions & perspectives,” 2011.
12.  E. Mirzaee-Ghaleh, M. Omid, A. Keyhani, and M. J. Dalvand, “Comparison of fuzzy and on/off controllers for winter season indoor climate management in a model poultry house,” Comput. Electron. Agric., vol. 110, pp. 187–195, Jan. 2015.
13.  I. Lahlouh, A. El Akkary, and N. Sefiani, “State feedback controller in a closed poultry house system,” in 24th International Conference on Automation and Computing, Newcastle upon Tyne, 2018.
14.  W. Wiboonjaroen and S. Sujitjorn, “State-PID Feedback for Magnetic Levitation System,” Adv. Mater. Res., vol. 622–623, pp. 1467–1473, Dec. 2012.
15.  S. Sujitjorn and W. Wiboonjaroen, “State-PID Feedback for Pole Placement of LTI Systems,” Math. Probl. Eng., vol. 2011, pp. 1–20, 2011.
16.  I. H. Akyuz, E. Yolacan, H. M. Ertunc, and Z. Bingul, “PID and state feedback control of a single-link flexible joint robot manipulator,” in 2011 IEEE International Conference on Mechatronics, 2011, pp. 409–414.
17.  I. Lahlouh, A. El Akkary, and N. Sefiani, “Mathematical Modelling of the Hygro-Thermal Regime of a Poultry Livestock Building: Simulation for Spring Climate,” Int. Rev. Civ. Eng. IRECE, vol. 9, no. 2, p. 79, Mar. 2018.
18.  International Commission of Agricultural Engineering, Ed., CIGR handbook of agricultural engineering. St. Joseph, MI: American Society of Agricultural Engineers, 1999.
19.  G. Conte, C. . Moog, and A. M. Perdon, Algebraic methods for nonlinear control systems. London: Springer-Verlag London Limited, 2007.
20.  P. J. Antsaklis and A. N. Michel, Linear Systems. Boston (MA): Birkhäuser,2006.
21.  R. Fonod and P. Kocsis, “State Feedback Control Design Using Eigenstructure Decoupling,” in 18th International Conference on Process Control, 2011, pp. 268–272.
22.  G. Ge, M. Zi, and Q. Junfei, “State-PID feedback control with application to a robot vibration absorber,” International Journal Modelling, Identification and Control, 2006.
23.  D. Luenberger, “Canonical forms for linear multivariable systems,” IEEE Trans. Autom. Control, vol. 12, no. 3, pp. 290–293, Jun. 1967.
24.  M. Valášek and N. Olgac, “Efficient eigenvalue assignments for general linear MIMO systems,” Automatica, vol. 31, no. 11, pp. 1605–1617, 1995.

(Click Here)

(Click Here)