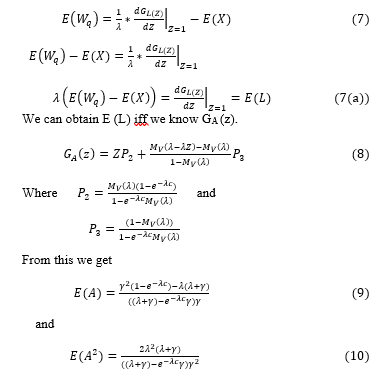1. Introduction

Queueing models are used to evaluate operational attributes of the service facility: service times, waiting times, number of customers including impatient customers in the system and more. Quite often, the service process includes delays.

The waiting time for service is one of the most key attributes of service process. Customer surveys in service systems demonstrate that holding up time is a key factor while assessing quality of service. Long waits may lead to feelings of anger and low customer satisfaction. Obviously, a balance must be brought between the number of servers that provide service and the factors like waiting times, cost etc.

In queues the situation where a server is unavailable for primary clients in occasional intervals of time is known as vacation.  Queues with server vacations have been studied over long period and also being adapted in many areas such as manufacturing, computer communication network models. In vacation queuing model the server completely stops service when it is on vacation. Queueing system with server vacations has pulled in the consideration of numerous analysts.

The subject of queueing systems with server failures is a prominent subject which has gained lot of attention of many researchers in the last five decades. In many realistic situations, the server may face unforeseen failures. For example, in manufacturing systems the machine may suddenly fail which leads a span of unavailable time until it is restored. Understanding the nature of the unreliable server in terms of unforeseen failures is vital as it influence system’s efficiency in terms of average Queue length and the customers’ mean waiting time. Hence, queueing problems with server breakdowns are more realistic phenomina. Single server queue subjected to breakdown and repair has been studied by number of authors.

Optimum utilization of server is vital for any system to run optimally. In this context we have explained the Vacation with the concept of Timeout and Server Breakdown with two types of repair facilities for an M^x/M/1 queueing model and also derived expected system length. Further, numerical solutions for various parameters by using batch size distributions are also illustrated.

did by the author [1] did numerous excellent surveys on the vacation concept and explained different kinds of vacation models. The paper [2] explained an M/G/1 Queueing System with interruption service and connection with the priority model. The paper [3] discusses queueing model with different types of server interruptions and also obtained the performance measures of the queue and customer delay. The authors [4] presented Vacation bulk queueing Model with setup time and server timeout and derived the average waiting time of this system. The author [5] has proved that the M/G/1 retrial queueing system with server breakdowns has a unique non negative transient solution and also studied asymptotic behavior of it. was explained by The authors [6]  explained a short survey on vacation models and also intends to provide a brief compact of the most recent trends in queueing systems with vacation in the previous 10 years. The paper [7] detailed M/G/1 type queue with Time-Homogeneous Breakdowns and Deterministic Repair times by using supplementary variable technique, The author [8] studied an M/G/1 queue in steady state with optional deterministic server vacation also designate the system as M/G/D/1 queueing system. The authors [9] were first studied vacation .They have shown the utilization of idle time of M/G/1 queue.

When the system is empty, the server will wait for settled time is known as server timeout; The paper [10] discussed the M/G/1 queue with vacation and timeout and elaborated the Average waiting time of the system and also developed for N-policy. The paper [11] detailed the analysis of optimization in single server queueing system with vacation and elicited the mean waiting time for single queue and also formulated for N-policy. The authors [12] studied M/M/1 Queue with vacation, server breakdown, Heterogeneous arrival as well as departure and also derived various constants of both system and queue in both un-operating modes  i.e.; either empty or  server breakdown.

The authors [13] explained an M^x/G/1 Vacation queueing model with Server Timeout and calculated expected system length for varying different bulk size distributions. The paper[14] detailed derivation of Queueing constants for an M/G/1 Vacation Queueing model with server breakdown, repair and Timeout. The authors [15] studied Optimal Strategy Analysis of N-Policy M/Ek/1 Vacation Queueing System with Server Start-Up and Time-Out and derived explicit expressions for the system length .

2. Model Description

 Consider single server queue where arrival rates are of compound Poisson process with mean rate ‘λ’. The server commences service in FIFO discipline. Whenever the system becomes empty the server waits for certain time ‘c’, which is called server timeout. At this time if a customer arrive the server return to the system and do service. At the end of this timeout period if no customer arrive the server takes vacation. Service may be interrupted due to Server breakdowns. Here we consider two kinds of repair facilities. Type–I repair is done if the customer’s service is interrupted due to server failure and the customer stays back in the system with a probability of 1-q to receive the remaining service whereas Type-II repair is initiated if the customer  whose service is interrupted due to server failure  quits the service zone and joins head of the queue with  a probability of  q. Service is restored immediately upon the repair of server.

3. Analysis of the Model

The customer arrivals are assumed under Poisson process with parameter ‘λ’.  The service rate is µ s per exponential law. The service time for a customer ’X’ assumed to be General with cumulative distribution function having mean E(x) and its second moment E(X²). The Laplace stieltjes transform function of X is , which is taken as

‘V’ is the duration of a vacation assumed to follow general distribution with CDF and Laplace stieltjes transform function of V is . The average value of V is E (V) and its second moment E (V²).

X and V are independent variables.

 The system may break down with a rate α, then system go for deterministic repair with rate d. After repair process completed then server start service to the customer.

 Let G_{L (M/G/1)} (z) is PGF  the number in system is given by [Ref 8]

 Let the number of customers in the system at the beginning of busy period is indicated as A. The probability distribution function of this variable A is P_A (a) =P [A=a], and corresponding z-transformation G_A(z) is given by

Let B denotes the number of customers left by an arbitrary departing customer. The Probability distribution of  B is P_B (b) with the corresponding z-transform G_B (z) as

Let L be the number of customers in the system at an arbitrary point of time. The distribution of L is  and corresponding Z-transform is given by

E (L) and E (L²) are the mean and second moments of L.

Specific batch size distributions

As the batch size ‘d’ may also varies and hence assumed as a random variable. In particular Deterministic, Geometric and Positive Poisson distributions are considered for it.

1.) If the batch size distribution is Deterministic, then the generating function equals to

                              D (z) = z^d

This gives mean  and second moment , where d is the average batch size.

2.) The batch size distribution is Positive Poisson, then the generating function equals to

 , where

This gives mean  and second momen , where m is the average batch size.

3.) If the batch size distribution is Geometric, then the generating function equals

D (z) = p [z^-1-(1-P)]^-1

This gives mean and second moment    , where  is the average batch size.

Let W_q denotes the waiting time in the system to determine system length. We get the mean of system length of the customer by using little’s law as [Ref 9]

Now substituting equations (9), (10) and k value in above equation (17) we get

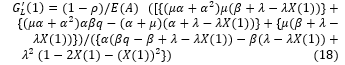 Thus by above expression, we obtain expected system length.

Particular case: If system suffers no breakdowns and repairs facilities then letting ß=0, d=0,q=0 and α=0 in the above expression (in equation 18)then the resulting expression is a known for the M/G/1 vacation queueing model with server timeout(Ref (12)).

4. Numerical Illustrations

Thus by using equation (18) and varying different parameters, we get some numerical illustration in Table 1 is given below:

Table 1: Effect of Different Variables (d, λ, µ, c, α, q and ) on expected system length for fixed values of d=2, λ=2, µ=50, c=1,  α=4 and =0.25.

Parameter	Parameter Values	Deterministic Distribution of E(L)	Geometric Distribution of E(L)	Positive Distribution of E(L)
D	2	6.5515	6.8621	8.0512
	3	10.7012	9.8528	11.7669
	4	14.2671	10.6947	16.0318
	5	20.4660	11.9441	21.4815
	6	26.5421	23.8526	27.7996
	2	6.5515	6.8621	8.0512
	6	9.3980	9.7938	11.6209
	10	10.5412	11.9592	14.2696
	14	12.4641	13.4027	17.6098
	18	13.0614	15.6601	24.6651
	50	6.5515	6.8621	8.0512
	60	6.5345	6.8364	8.0277
	70	6.5205	5.8154	7.9902
	80	6.5088	5.7979	7.9613
	90	6.4989	5.7830	7.9479
C	1	6.5515	6.8621	8.0512
	2	6.5495	6.8582	8.0473
	3	6.5489	6.8571	8.0432
	4	6.5445	6.8494	8.0383
	5	6.5421	6.8475	8.0364
	0.25	6.5515	6.8621	8.0512
	0.75	3.3932	4.6704	5.0478
	1.5	1.2247	2.4775	3.6639
	2	0.9712	1.2177	1.3564
	2.5	0.8304	1.0865	1.0621
	4	6.5515	6.8621	8.0512
	6	7.3980	8.3628	10.3239
	8	9.4412	11.2947	14.2496
	10	11.4641	11.8441	18.6098
	12	14.0614	23.8526	24.6651

As d, λ, and α were increasing then expected system length E (L) is also increasing.

As µ, and c are increasing then expected system length E (L) is decreasing.

5. Conclusion

In this model, we have derived an expression of expected system length for M^X/M/1 vacation queueing model with two varieties of repair facilities and server timeout. Sensitivity analysis is carried out on the system length.

Conflict of Interest

The authors declare no conflict of interest.

Acknowledgment

Uide Dr. Kotagiri Chandan and affiliated institutes for their continuos support

1. Doshi, B.T (1986), Queueing system with vacations. A survey on queueing system: Theory and Applications. 1(1), 29-66.
2.  D. Gaver Jr. (1962), A Waiting line with interrupted service, including priorities. Journal of the Royal statistical Society, Vol.B24:73-90.
3.  Dieter Fiems, Tom Maertens and Herwig Bruneel (2005), Queueing system with different types of service interruptions, SMACS Research Group, Department TELIN (IRO7), {df, tmaerten,hb}@telin.UGent,Belgium.
4.  E.Ramesh Kumar and Y. Praby Loit (2016), A Study on Vacation Bulk Queueing Model with setup time and server timeout. IJCMS, 5(12), 81-89.
5.  Geni Gupur, (2010), Analysis of the M/G/1 retrial Queuing Model with server breakdowns. Oper. 1:313-340.
6.  Jau-Chuan Ke, Chia-Huang Wu and Zhe George Zhang, (2010), Recent Developments in Vacation Queueing Models: A Short Survey. Operation Research Vol 7, No 4.3-8.
7.  K.C. Madan, (2003), An M/G/1 type queue with Time-Homogeneous Breakdowns and Deterministic Repair Times, Soochow Journal of Mathematics Volume 29, No. 1, pp. 103-110, January 2003.
8.  K.C. Madan, (1999), On a M/G/1 Queue with Optional deterministic Server vacations, Mentron, LVII, 3-1, 83-95.
9. Levy.Y and Yechiali. U, (1975), Utilization of Idle Time in an M/G/1 QueueingSystem.ManagementScience,22,202-211. http://dx.doi.org/10.1287/mnsc.22.2.202.
10.  Oliver C. Ibe (2007) Analysis and optimization of M/G/1 Vacation Queueing Systems with Server Timeout, Electronic Modeling, V.29, no. 4, ISSN 0204-3572.
11.  Oliver C. Ibe (2015), M/G/1 Vacation Queueing Systems with Server Timeout, American Journal, 5, 77-88. http://www.scrip.org/journal/ajor.
12.  R.P.Ghimire and Sushil Ghimire, (2011), Heterogeneous Arrival and Departure M/M/1 Queue with vacation and service Breakdown. Management Sciences and Engineering, Vol. 5, No. 3, pp. 61-67.
13. Y.Saritha, K.Satish Kumar and K.Chandan (2017), Mx/G/1 Vacation Queueing System with Server Timeout.International Journal of Statistics and Applied Mathematics, 2(5): 131-135.
14. Y.Saritha, K.Satish Kumar,V.N.Rama Devi and K.Chandan (2018), M/G/1 Vacation Queueing System with breakdown, repair and Server Timeout. Journal of emerging Technologies and innovative Research(JETIR), Volume 5, issue 2 2349-5162.
15. K.Satish Kumar, K.Chandan and Y.Saritha. (2018), Optimal Strategy Analysis of N-Policy M/Ek/1 Vacation Queueing System with Server Start-Up and Time-Out.JETIR, Vol 5, Issue 10, 380-385

(Click Here)

(Click Here)