1. Introduction

This paper is an extension of work originally presented at the International IEEE Congress on Information Science and Technology [1].

Starting from the beginning of this century, social networks have significantly evolved, and the progression of social media platforms (Facebook, Twitter, LinkedIn, etc.) has been well documented in a significant number of publications. In the contemporary era of connectivity, the majority of organizations complement their traditional marketing strategies with digital campaigns that rely heavily on social media channels. Due to its increase in popularity, social media has become integral to organizations’ advertising and marketing campaigns, representing a cost-effective and efficient channel through which companies target and communicate with members of a given audience.

Since their inception in the late 90s, the value of social networks (SNs) has dramatically increased to reach billions of dollars. As such, they represent an attractive investment proposition, especially in the marketing sector. Their rise in popularity and social and economic implications has also attracted significant research attention. One area of interest particularly notable in recent times is the prediction of missing links [2, 3].

1.1. Predicting Links in SN

By using graph theory concepts, SN can be represented as a graph of vertices and edges: G(V, E). The vertex V represents a user while the edge E represents a link. Figure 1 shows a simple representation of a social network.

The issue of predicting links in SN is concerned with the forecasting of possible connections and interactions that can be observed between various members within a certain network. As explained in [4], considering an SN, G, at a certain time, t, the objective of link prediction here is to predict possible new links or the breaking of existing ones at a later time, t~. Several researchers have expressed an interest in predicting existing, expected, and missing links by developing a range of different methods. Despite the fact that several methods have been proposed, however, [5] indicate that none of them are reliable in effectively predicting the missing links.

An important feature of link prediction in SN is concerned with identifying missing links. Having the ability to predict missing links would provide us with clues of how SN evolves within a range of settings. Predicting missing links has important connotations, for example, in the academic world, where doing so would help to identify possible academic collaboration in certain fields of interest [6,  7].

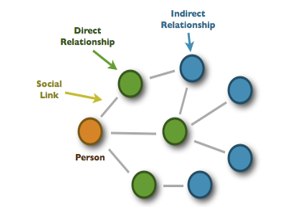Figure 1:  Simplified representation of SN

A further area where social link prediction could be of use is within criminal investigation; for example, similarity-based link-prediction methods are viable for identifying links between members of criminal networks. Identifying possible missing links in criminal networks can be achieved by exploiting node similarity in noisy or incomplete situations [8]. Predicting broken links is also of paramount importance within commercial settings, as marketing, customer service, and customer experience strategies based on link prediction can maintain customer loyalty. In bioinformatics, biology, and healthcare, the prediction of missing links can assist organizations in locating the relevant specialists who are able to receive future referrals, while within gene expression networks [9] they can be employed to better understand protein-protein interactions. Elsewhere, as explained in [2, 10], within security-related networks, link prediction can be used to detect suspected communications that countries are more likely to find harmful.

Social networks contain significant amounts of data; as such, it is not possible to collect all the information connected to a user’s relationships. Link prediction, therefore, represents a viable means by which it is possible to apply an understanding of known relationships between users to estimate unknown relationships.

The existing literature highlights a continual increase that has occurred in the number of link-prediction methods that are capable of predicting SN links. This vast rise in the number of such methods is exponential to a large number of publications in renowned journals or conference proceedings that either propose a new method of predicting links or else to improve the accuracy and efficiency of an existing approach. Figure 2 depicts the number of articles published in Scopus indexed journals or conference proceedings. As the graph reveals, there has been a steady rise in the number of articles published that have focused on link prediction practices. Subsequently, many solutions have been introduced to handle the problem of accurately and efficiently predicting the missing links.

A link-prediction method that exploits the information diffusion feature was discussed in [11]. This study demonstrated the correlation between information diffusion processes and the creation of new links. The proposed method managed to enhance the accuracy of link prediction by virtue of information diffusion and was tested on a Sina Weibo dataset. The experimental data revealed that the proposed method outperformed approaches that rely on topological features alone.

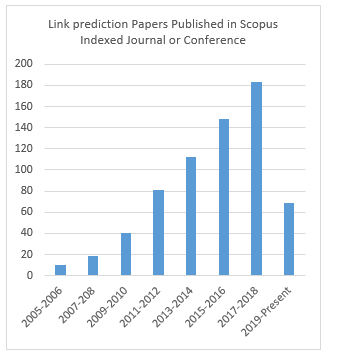Figure 2: Papers related to link prediction published in Scopus-indexed journals or conference proceedings

Several link prediction approaches that are based on a deep belief network were presented in [12]. The results obtained from the experiments on datasets collected from different sources revealed that the methods effectively predicted link values and exhibited a remarkable generalization capability among the studied datasets.

Due to the vast amount of data in social networks, achieving efficiency within link-prediction methods represents a significant challenge. To address this problem, [13] proposed two algorithms for link prediction. The proposed algorithms solved the efficiency problem by adopting low-rank factorization models, while also proving very efficient compared to other methods. As such, the study represents a significant step forward in the challenge of developing an efficient link-prediction model.

Another important problem that needs to be addressed concerns the accuracy of link prediction approaches. [14] developed an innovative link-prediction method that aimed to improve the accuracy of link predictions. The experimental findings revealed that the proposed approach outperformed many other methods in terms of accuracy and scalability and the associated runtime was significantly less than that observed in previous studies. However, although the proposed approach did enhance link prediction accuracy, it remains untested on large network data, which may see its efficiency become undermined.

Improving the accuracy of link prediction can also be achieved using methods that predict links in uncertain frameworks. [15] proposed a new approach for addressing the problems of link prediction in the context of an uncertain framework based on the theory of belief functions. Results obtained from the experimental work of [15] outperformed traditional approaches.

Another problem related to link prediction in signed SNs concerns the sparsity of data. To alleviate this problem, [16] proposed an innovative approach that is capable of exploring the personality of the user using social media. The experimental results obtained indicated that a complementary relationship exists between the signed link prediction problem and personality information.

An interesting state-of-the-art method for facilitating link prediction is the use of the temporal regularity in interpersonal communication as a means of prioritizing weighted edges in network graphs [17]. Compared with other methods, this method predicts links even if there is a scarcity in the number of edges needed for analysis.

A contrasting similarity-based link-prediction method, based on fuzzy link importance, was presented in [18]. The method performed well, using two strategies to achieve its objectives. Firstly, for the selection of the neighbor, the distance between nodes was used. Secondly, to find the relevant link, the fuzzy link importance was employed. By using these strategies, the method has obtained sound results.

An approach aiming to solve the problem of link prediction problems in large complex networks was proposed by [19] following two steps. In the first step, the complex network is transformed into a different simple network, before the second step uses probability to predict the possible links. The experimental test results indicate that the method achieved promising results.

Methods for predicting temporal links in temporal networks have been introduced. For example, [20] proposed an innovative approach based on a semi-supervised learning network with the aim of predicting current and future links. The approach was tested using real data. The results obtained from the experimental test demonstrated that the approach was very effective and highly scalable.

A myriad of similarity-based methods has been introduced to address link prediction problems. However, methods of this nature require substantial data to work effectively. Recent methods have been introduced to alleviate such problems, and approaches based on similarity indices have accomplished considerable efficiency. For example, [21] proposed a method that uses a clustering coefficient index found to outperform many existing approaches. The improvements the approach exhibited were attributed to the use of an index of clustering.

Within the context of multiple networks, the link prediction problem was discussed in [22]. In terms of accuracy, the supervised learning method achieved 92.5%, which is very promising. The unsupervised method achieved a resounding accuracy result of 97% using normalized discounted cumulative gain.

Another interesting method proposed as a means of addressing the problems of similarity-based link prediction approaches was put forward by [23], which successfully managed to address the issue of lack of efficiency. The experimental results revealed that the LDR index enhanced the prediction performance in undirected networks. However, the researchers highlighted a need to investigate the method’s application further within directed and signed networks.

Many researchers have achieved remarkable improvements in link prediction within the context of social networks. However, studies that address trusted link prediction are very few. Recently, [24] proposed a method that sought to forecast links by using the user’s most important features. The experimental results revealed that the method outperformed many existing approaches in terms of effectiveness. Moreover, the quality of community detection was improved.

In the past, research that investigates issues related to link prediction in signed networks has been very scarce. Only recently have we witnessed an increase in the number of studies that discuss issues related to link prediction in signed networks. For example, [25] proposed a fresh approach with experimental results that show a high quality in terms of the accuracy and efficiency of link predictions.

Many further new methods have been introduced with the aim of improving link prediction accuracy, for example, [26] has proposed a method that achieves good accuracy using associated degrees.

A more interesting method for link prediction was proposed by [27], which employed the level-2 node clustering coefficient. As previously described, most link-prediction methods suffer from either lack of efficiency or accuracy. Plus, increased efficiency can lead to a reduction in accuracy. [27] suggested a method that was tested experimentally over 11 real-world datasets. The obtained results indicated that the method outperformed many of the state-of-the-art existing methods in terms of accuracy.

In dynamic SNs, categories of users exert social influence on other members within the social network. These individuals are commonly referred to as influencers. Influential users play a fundamental role in digital marketing [28]. As such, predicting links to and from influential users is of paramount importance for many organizations. [29] introduced a method aiming to predict influential links. The approach was tested experimentally and the test’s findings revealed that the proposed approach outperformed comparable link prediction metrics. Moreover, the link prediction performance was improved in comparison to that associated with classical topological metrics.

Low link prediction accuracy remains a major challenge that requires attention. A myriad of methods and algorithms has been introduced by many research field scholars. A current approach that aims to address the problem of low link prediction accuracy, which is based on matrix factorization, is proposed by [30]. The experimental results of the method indicate that it achieves a higher prediction accuracy than existing methods.

Despite the fact that matrix-factorization-based methods have achieved good security, such methods suffer from the problem of having to build the adjacent-matrix. [31] has developed a technique to address the problem of matrix-factorization-based methods by fusing the adjacent matrix and some key topological metrics in a unified probability matrix. The [31] models were experimentally tested with real data, with the results of the experiment revealing that the proposed models achieved an impressive link prediction performance.

Another important and interesting method that has achieved great link prediction accuracy was put forward by [32], which used H-index and the influence of degree. The method achieved remarkable link prediction accuracy by utilizing information about the endpoint node.

Among the methods that have been developed to utilize real node influence and improve link prediction accuracy is that of node ranking [33]. This method uses the concept of node ranking to improve link prediction accuracy.

 Even though there are some problems inherent in similarity-based methods, they have achieved considerable results in terms of accuracy and efficiency. However, further such improvements will be required. A method that is based on the kernel graph, which utilizes the structural information extracted from a signed social network, was proposed in [34]. This method involves initially generating a set of subgraphs with different strengths of social relations for each user. Having been tested with real data, the experimental test results revealed that the method achieved considerable link prediction performance on the two types of positive and negative links. Moreover, the accuracy and F1-Score exceeded that of existing methods, indicating that there is room to improve accuracy.

More methods that use a similarity index for link prediction have recently been introduced. A method that took the attribute similarity between the node pair into consideration, named attribute proximity, was discussed in [13]. The experimental test results showed that it achieved higher accuracy than approaches that didn’t take node attribution into account.

1.2. Link Prediction in Dynamic SNs

Dynamic networks can be used to describe members that exhibit varying dynamics over time [1]. In such a network, a new member joins, existing members may leave the network, and members create or break relationships [46]. As a consequence of this phenomenon, the network can expand or shrink. For this reason, there is a compelling need to take dynamic changes into consideration when developing approaches that can accurately predict new, current, or missing links. Link prediction in temporal SNs is more challenging due to the continuous network changes. The dynamic changing nature of temporal SNs will result in the emergence of different types of sub-graph. Many applications have attempted to exploit this nature of networks, for example, countries seeking to beef up their security can use such features to predict criminal links, and online recommendations [4]. Biological networks can also utilize temporal networks, with a vast number of applications having been proposed that do so, [57] developing innovative methods for detecting protein complexes. The method proposed by [57] exploited the dynamic nature of protein, while [35] has developed a model that detects the progress of a community over time by utilizing the temporal nature of SNs. [36] discussed an interesting method that predicted links in a dynamic SN based on three metrics. The proposed method was experimentally tested on DBLP data and the results obtained indicate that the method achieved superior results to alternative approaches. The predicting of future links in social networks using the proximity of node is discussed in [37]. In this approach, future interaction can be obtained from network topology alone.

The structure of social networks is rapidly evolving. To leverage this evolving structure, [38] proposed a method that exploited characteristics calculated by a known time prediction of measures computed using a pair of nodes. The method was tested using real data. The experimental results obtained revealed that the approach achieved high accuracy.

The influx of methods that are capable of predicting future relationships in dynamic SNs continues to increase. For example, [39] introduced a method that utilizes learning automata for link prediction. In the same direction another new method proposed by [40] uses learning automata to predict links in stochastic SNs. The method was tested using data collected from social networks and has achieved sound link prediction accuracy. One of the interesting features of this is that it deals with online stochastic SNs that can encounter complex online variations.

Clustering, one of the prominent data-mining techniques, has also been employed for predicting future links in dynamic SNs. An interesting method that uses the clustering approach for predicting future links is proposed by [41], while another method is discussed in [42]. These two methods have obtained sound results in comparison with existing methods.

Deep learning is one of the data-mining techniques that has received more interest from researchers working in the field of data mining and machine learning. The nature of this technique makes it suitable for use in dynamic SNs. [1] discussed a number of techniques that predict links using deep learning. Also, a viable approach that successfully managed to predict links using machine learning is discussed in [43].

Some link-prediction methods suffer from a lack of precision. However, some researchers have attempted to alleviate such a problem by proposing different types of techniques. For example, [44] proposed an approach that utilizes community information to improve prediction accuracy. Taking the same approach, [45] introduced a technique that exploited the structure of community information to predict new edges and hence improve link prediction precision.

One of the most important features of online SNs is their rapid change over time [46]. Currently, most of the methods used for predicting links depend on structural SNs. There is a compelling need for methods that are capable of predicting links in dynamic SNs. Moreover, the required methods should also possess high link prediction accuracy and efficiency. Organizations intend to exploit online SNs for a number of applications and require information on state-of-the-art methods that can be used to predict possible links. The main objective of this paper is to discuss and analyze the most prominent link-prediction methods that are able to accurately and efficiently predict links in dynamic SNs.

This paper is organized as follows. Section 2 discusses the problems of link prediction. The next section discusses the strategies used by link-prediction methods to solve the problem of link prediction. This is followed by discussing and analyzing existing work. The paper wraps up with conclusions and future work.

2. Problems of Link Prediction

A simple question and answer summarizes the problem of link prediction. As discussed in [47], if we have SN at a certain time, t1, after a period of time, t2, can we predict a possible link between members of the SN? Many methods have been introduced that use structural SNs but, in real life, SNs are dynamic. In this section, we try to provide an overview of the problems of link prediction in dynamic SNs.

2.1. Link Prediction in a Temporal Network

A temporal network is a network that evolves over time. For predicting the emergence of links in such a type of a network, time factors are crucial [48]. Details on how links can be predicted using a temporal network can be found in [49]. The main problems and challenges of predicting links in a temporal network that require addressing are related to the changing nature of the network over time. Many methods and techniques have been proposed to address this problem. For example, [48] introduced a technique to exploit the general network structure and managed to successfully predict links in the process. [5] proposed a technique using graph theory to predict links, and [50] used community structure information to do so. An efficient method proposed by [51] produced far better results than many contemporary temporal link-prediction methods.

In [52], the authors explored methods of inferring links in a special type of network; ego-networks – where there is a scarcity of information about neighbors. The proposed methods introduced numerous approaches to retrieve information about communities. In doing so, they have improved the prediction of links compared with other methods that use structural SNs. An interesting method that determines the edge weight based on a calculation of the scores using spectral analysis is given in [17]. The method achieved good prediction results.

An effective and scalable method for predicting links within a real-world temporal social network was presented in [20]. [53] proposed a method that takes into consideration the time features of the network. The method captured the importance of timestamps in the interaction between network nodes and the experimental results showed significant improvement of link prediction. In the context of a temporal network, [54] proposed a method that predicts links by using a cross-temporal concept, which involves inferring the nodes at different time intervals. The method was tested experimentally using real-world data and the results showed sound improvements in the link prediction accuracy.

2.2. Link Prediction in Heterogeneous Networks

      In SNs, there are two major types of networks: homogeneous networks and heterogeneous networks. The homogeneous networks assume that all the nodes and edges are of the same type while, in heterogeneous networks, there is variation in the nodes and the links between them. The majority of the existing link-prediction methods deal with homogeneous SNs. In the real world, the majority of SNs are heterogeneous with different types of nodes and edges that pose many challenges requiring intervention. For addressing such problems, many new link-prediction methods have been introduced. For example, the work of [55, 56,  5,  57] and recently [58].

2.3. Link Prediction with Active/Inactive Links

      Interactivity in SNs is generally represented by sending e-mails, receiving phone calls, commenting on messages, etc. Historical information related to interactivity between nodes in the networks, such as the timestamp, is likely to improve the accuracy of link prediction. Using the temporal features of dynamic SNs has been proven to improve accuracy too [4].

2.4. Link Prediction Scalability

The era of big data has emphasized the importance of efficiency for link prediction algorithms. The link prediction algorithm scalability remains questionable unless the algorithm is tested and evaluated with a huge amount of data. However, most of the current existing link-prediction methods have been tested and evaluated using limited datasets, which make it harder to ensure their scalability. The issue of algorithm scalability remains one of the challenges that need to be addressed. Attempts were made by [59] to develop a scalable link prediction algorithm. The developed algorithm managed to predict links using features of endpoints and neighborhood, adopting the locality-sensitive hashing algorithm to enhance the scalability so that the proposed approach could effectively predict links in large networks spanning long-term sequences.

3. Link Prediction Strategies

      This section discusses the strategies used for link prediction, which include similarity-based methods, maximum likelihood methods, clustering-based methods, probabilistic models, fuzzy link methods, and matrix factorization-based link-prediction methods.

3.1. Similarity-based Strategies

      Similarity-based link-prediction methods are among the first and simplest methods used in link prediction. The idea behind this class of methods is that each node pair – say n1 and n2 – is given a score that reflects the similarity between n1 and n2. The algorithm then ranks the pair of nodes based on their score, and the node pair with the highest score is most likely to have a link between them [60]. Nodes show more similarities if they have shared neighbors.

There are some problems and challenges associated with the link-prediction methods that use a similarity score. As discussed in [18], predicting the link is based on computing the rating and the selection of the neighbors by using similarities between the pairs. If the algorithm fails to find enough information on the ratings, there will be problems with computing the similarity. Moreover, the accuracy of link prediction will be negatively impacted by the number of neighbors.

Similarity-based link-prediction methods are not confined to structural SNs. In dynamic SNs, a number of methods have also been introduced. For example, [4] and [50] proposed an interesting method that employs similarity indices in dynamic SNs. The model proposed in [4] is based on the Covariance Matrix Adaptation Evolution Strategy. Plus, a modified similarity-based link-prediction method was discussed in [61]. The approach was experimentally tested and evaluated using real-world data. The results obtained indicate that the method outperformed existing similarity-based link-prediction methods in terms of accuracy. Two improved algorithms, based on the similarity method that applies the network topology sufficiently, were presented in [62]. The experimental results of the two improved algorithms reveal that the prediction performance was far better than the existing traditional one.

Some efficiency improvements have been made to the similarity-based strategy. For example, [23] proposed an algorithm that improved computation efficiency. The improvements were made by the algorithm with the virtue of using linear computation. Further improvements in terms of effectiveness, efficiency, reliability, and strength were achieved using the method introduced by [24]. This approach made use of several user features to predict trusted links. Additional improvements in terms of the accuracy of link prediction were achieved by [26]. Their method used strategies that depend on the depth of the path passing from the source to destination nodes and the associated degree.

Accuracy, which is consistently used to evaluate link-prediction methods, represents an important consideration when developing and implementing any method that can be used for predicting links. A modified similarity-based method employing graph theory was proposed by [34]. Their method achieved significant improvements in the accuracy of predicting links compared with existing methods, thereby demonstrating that similarity-based methods continue to play a significant role in link prediction. The accuracy of similarity-based link-prediction methods was further improved by [63]. Their method achieved a remarkably high prediction accuracy by using a similarity index called attribute proximity. The authors concluded that the higher the similarity between the topological neighborhoods of two nodes, the more likely that a link will emerge.

3.2. Maximum Likelihood Algorithms

Maximum likelihood algorithms for link prediction is a concept applied to determine the parameter distribution of the network structure. In link prediction, the assumption made here is to organize the network structure and then maximize the likelihood of the observed structure. Based on this concept, a number of methods have been developed. For example, [55] employed the concept of maximum likelihood to predict links in SNs. With limited datasets, the method obtained good results.

Link-prediction methods based on maximum likelihood face practical applications related to the time taken by the algorithm to converge, especially if the dataset is very large, implying that the algorithms are not scalable.

3.3. Probabilistic Models

An interesting class of methods used to predict SN links is based on a probabilistic concept. This approach can be applied to both static and dynamic SNs. In dynamic SNs, [64] employed a probabilistic concept to deal with the complexity of a non-linear dynamic created by the data features. The model managed to predict links with good accuracy. Additional methods were proposed using this concept to predict links such as [55, 56 , 5]. Some methods combined the features of graph theory and probabilistic concept to predict links in SNs [65]. This hybrid method is very scalable due to the innovative approach used to approximate the probability of links.

In [66], the authors proposed an algorithm framework that combines probability with the Hamiltonian structure to predict links in SNs. The algorithm was tested and evaluated experimentally using numerical simulation data. The results obtained from testing the algorithm showed that it achieved a very high accuracy compared with the best available link-prediction methods. The algorithm also successfully managed to identify and uncover the missing links.

Despite the fact that link-prediction methods based on probabilistic features have achieved sound results in predicting links in SNs, the main problems of these methods center around efficiency. The computational time needed by the method is very high, so there is a need for reducing this reliance.

3.4. Clustering-Based Link-Prediction Methods

Clustering-based link prediction approaches have played a considerable role in enhancing the efficiency and accuracy of links inferencing. These methods have been discussed in several studies, for example, [11, 67, 21, 27].

In [11], the method achieved better improvements in the accuracy of links forecasting as the number of clusters grew, whereas [67] proposed a cluster-based method that used clustering information to predict the missing links. Their method was tested on three large-scale networks, with the experimental results revealing that it outperformed other approaches and, more interestingly, that information about link clustering has improved the accuracy of link prediction. [21] used an index that took into consideration more information related to the structures provided for link forecasting to enhance its accuracy in comparison to alternative indices. The accuracy of the method proposed by [21] was compared with twelve representative link-prediction methods, and the findings revealed that it exceeded their performance.

The approach proposed by [27] first involved extracting similar neighbors and grouping them into clusters, then computing the coefficients of the cluster up to two common levels. Their method exceeded the performance of all the alternative baseline methods. The only method that outperformed theirs is Node2vec, albeit with medium accuracy.

 3.5. Fuzzy Link-based Methods

Link prediction based on the fuzzy concept has only recently been applied. For example, [18] proposed a model based on this concept with the proposed model, when tested and evaluated on real data, achieving considerable accuracy improvements. [68] proposed two methods that employ the concept of fuzzy-link prediction. The first approach used the concept of a fuzzy soft set, while the second employed the Markov model concept to improve the efficiency of link-prediction methods. They claimed that their models achieved better prediction than the existing approaches.

3.6. Matrix Factorization Methods

The simple idea behind matrix factorization is to decompose a complex matrix into a simpler one to make it possible to compute more complex operations. Numerous link-prediction methods based on matrix factorizations were proposed that have effectively improved performance in terms of the accuracy and efficiency of link prediction. For example, [31] propose a framework that can be used for link prediction incorporating the matrix factorization concept.  [69] discussed an interesting link-prediction method that uses the concept of matrix factorization. The proposed method produced better results in terms of link prediction accuracy when compared with other methods. A recent study based on matrix factorization was discussed in [30]. Although the method of [30] achieved high prediction accuracy, the data was relatively limited as it was confined to sales datasets. As such, further evaluation involving more complex datasets is required to confirm its level of prediction accuracy.

4. Analysis and Discussion of Existing Methods

In the previous sections, we have discussed the challenges and problems of predicting the emergence of new links using a special type of SN; namely, dynamic SNs. Furthermore, we have also discussed the different types of link-prediction methods proposed by many scholars working in the SN field. This section discusses the most current solutions introduced by researchers in the field of predicting links in SNs. The main topics to be discussed in this section start with the summary of the proposed solutions for addressing links prediction problems, followed by datasets used, the main features of link prediction, the techniques used in link prediction, and concluding with the evaluation and accuracy measures. A summary of the solution’s evaluation results is depicted in Table 2.

4.1. Summary

Once online SNs had become an important platform for the exchange of a huge amount of data between users, their existence attracted a significant number of scholars intending to study how these networks evolve over time. The emergence and deletion of links help researchers to understand the dynamic nature of SNs [2].

In the past two decades, many link-prediction methods have been introduced, implying that the problem is not new. However, the new and most challenging SN-related task concerns the forecasting of links in dynamic SNs, which are characterized by growing or shrinking networks. The majority of the work that has been performed in the area of dynamic SNs to date has been conducted with the acknowledgment of the importance of a dynamic nature within the network. Many scholars have taken into consideration the changing time features of the SN by using past information related to the node transactions, while others used the temporal feature of community structure [50]. These approaches forecast the future importance of a node based on eigenvector centrality. Subsequently, this view of future importance is used to predict links.

Some researchers have tried to develop new techniques for predicting future links using historical data. Their main objective is to improve the efficiency and accuracy of the methods applied. A model for link prediction in dynamic SNs using deep learning is discussed in [1]. Another model for link prediction based on a triad transition matrix, using statistical data, is given in [56].

The model discussed in [55] predicts future links by using the Euclidian latent distance. Nodes that exhibit closeness in the Euclidian distance are more likely to emerge as links. [4] proposed a model depending on the local information of nodes to predict future links in the dynamic SNs, while [5] introduced a model that uses graph theory to predict links by including temporal features.

In [17], it is introduced a method for link prediction based on graph theory. The method used the spectral analysis technique to calculate the score for each edge in the network graph. Based on this score, the edge weight will be determined. The method was tested and evaluated using real-world data, with the obtained results indicating that the method has enhanced the prediction of links. More interesting, however, is that the edges used in the analysis were very limited.

4.2 Datasets Issues

Most of the research conducted for the sake of developing link-prediction methods involves the use of some form of data that is either artificial or real world, as with [64] and [55]. The major problem concerning the datasets used for testing and evaluating the link-prediction methods is the absence of standardization [2]. Researchers have used numerous SNs of various sorts and sizes according to their proposed model and there are several dataset types available for researchers to use. The majority of networks used in the existing literature include collaboration networks, online SNs, generated datasets, and friends and family e-mails. [55, 56, 5] have used collaboration SN datasets. [64] employed two biological SNs. Most of the datasets used are small in size, with the exception here being [4] who employed a moderately large size of the online SN (Twitter) for the development of their method. For testing and evaluating their method, [50] used five email SNs. [56] employed a merging of two datasets; namely, scientific collaboration networks and email. Table 1 shows a summary of the datasets used by various researchers surveyed in this paper.

Table 1: Datasets used by researchers [1]

Datasets	No. of nodes	No. of links
Irvine Msg	896	2,201
Enron	200	714
News Words	503	15,638
Manufacturingmails	167	3,250
Robot	352	1,611
Twitter (RRNs)	5.71*106	49*106
DBLP	437,515	1,359,471
astro-ph	55,233	644,496
Friends and Family Emails	1,130	1,344
Math	24,818	506,550
Ask	159,316	964,437
Super	194,085	1,443,339
Stack	2,601,977	63,497,050

From the literature that we surveyed, we found that the choice of suitable dataset depends on the judgment of the researchers who want to develop the link-prediction method and evaluate its performance using the collected data. Furthermore, the datasets used in many applications are synthetic, artificial or generated [64] [55] which might raise some concerns about the results obtained using such a type of dataset. Moreover, the size of the data used in testing the performance of the methods is not large. Another problem regarding the data is the nature of the datasets which, in many cases, is static and needs to be used to test the method based on the dynamic network. Some researchers have attempted to address this problem by including features of a temporal network [64, 55, 56, 5]. As most SNs grow and shrink over time, indicating that these networks are dynamic, it will prove more interesting for link-prediction methods to be applied in these dynamic SNs rather than structured ones. To judge the practicality of such methods, the datasets used should be real and applicable for link predictions. As many studies indicate that the datasets used for evaluating the developed methods are either static, artificial, or with a sample size, these issues represent great challenges that need to be addressed. These challenges point to the important need for setting database standards that will be used for evaluating the performance of all these methods.

4.3. Features Used in the Link Prediction Process

The two main features used to predict links in dynamic SNs are node attributes information and network topology. Both features have been used by numerous studies to predict links in dynamic SNs. For example, [55] developed a model that employed the latent space concept and used the local topologies feature. The model predicts links based on past information, assuming that if there are two nodes, n1 and n2, which have links in the time, t-1, then mostly likely they will be gaining a link at a time, t.

The model proposed by [4] employed the two predominant features used to predict future links in dynamic SNs; namely, the network topology and node attributes. A test of this model using a vast amount of data indicates a high convergence with astonishing precision. Unlike the majority of the techniques proposed to detect dynamic community, [4] proposed a model named Hierarchical and Overlapping Community Tracker (HOCTracker) that is capable of detecting the progression of an overlapping community in dynamic SNs. The results obtained from the experimental test of the model indicate that the community structure detected is far better than the best available methods.

The model proposed by [56] uses the concept of a triad transition matrix to discover the dynamic pattern of networks. The main feature used is a local topology network and observations of the recorded network history. The model merges statistical characteristics with the topology of the network. This merger resulted in a method with the strength to perform better in detecting the evolution of a network. The model introduced by [5] incorporated the available past information about links on the current SN state. The model shows that including a timestamp of the historical interaction improves the accuracy of predicting new links. The technique used by the model to predict links is a joining of the graph with the temporal information included in the evolving SNs.

4.4. Techniques Used in Link Prediction

Link-prediction methods employ a variety of approaches and strategies in the form of a cluster-based, similarity-based, or fuzzy link, etc. The most appropriate prediction technique is selected on the basis of the features used in the link-prediction method. In similarity-based models, the method predicts the links among nodes based on a similarity score computed among the pair of nodes. A pair of vertices with high similarity value is most likely to foster a relationship or link in the future. Methods based on maximum likelihood predict future links between two nodes by identifying a centric node. If the likelihood that the two nodes fall in the radius of that centric node is high, then there is a possibility that a link might emerge between them. Methods based on a probabilistic approach use probability to predict the future links between two nodes in the dynamic SNs. The methods predict the links by calculating the probability of the edge weights of the two nodes and the probability of the neighboring nodes. The clustering-based link-prediction methods use a node clustering coefficient to predict the link. The technique first computes the clustering coefficient then uses it to predict the future link [27].

The research of [4] is focused on a node’s local feature, for which they use the similarity index to predict the emerging link. The work of [55] used an approach that ranks the likelihood of two vertices expected to be linked based on the frequency of joining in the test set.

The model proposed by [56], which is based on the Triad Transition Matrix, relied on the probabilistic approach in that it contained triad transition probabilities in the network. The local probabilistic model was extended by [5] to predict links using the timestamp feature and demonstrating the incorporation of link weight into the prominent link prediction approaches. [50] model integrated various kinds of information into the SNs, such as node centrality and temporal information.

Another model that relied on the probabilistic approach uses Conditional Temporal Restricted Boltzmann Machine (CTRBM), described by [64], to forecast emerging links on individual transition variance and the influences of local neighbors.

4.5. Methods Evaluation

This section discusses the diverse evaluation measures and metrics employed by the different types of methods proposed by various researchers. The evaluation in terms of method accuracy and efficiency represents an important factor for its applicability and acceptability. To date, there are no common metrics and measures that can be employed to evaluate these methods. This lack of common evaluation metrics and measures, coupled with the absence of standardized datasets, entails that it is very hard to assess each solution and, as such, we cannot present a reliable and valid conclusion as to which is the best in terms of link forecasting in dynamic SNs.

The methods explored in this study can be evaluated either by two machine-learning measures; namely, receiver operating characteristics (ROC) [70] and the area under ROC (AUC) or other measures. The interpretation of the values of these measures depends on the method, as each method has features that are different from the others.

For example, when evaluating two models that have an AUC score close to each other, it will be very hard to determine which one is the best to select. As such, [64] employed a measure that computes the sum of the absolute difference to distinguish between various types of models. The methods discussed in [4, 55, 15, 17] employed ROC and AUC for evaluation.

Researchers in [56] employed another means for evaluating their methods in terms of efficiency. They have used two evaluation techniques, with the first one being known as average normalized rank (ANR), and the second known as discounted cumulative gain (DCG), which is employed for node ranking. ANR was employed to directly pinpoint the location of the important item in the ranking. In comparison, [20] used two measures, F1Score and Kendall’s Tau Coefficient (KTC), to evaluate their methods.

From the surveyed and discussed methods, we found that each researcher has typically selected the evaluation metric and measure that best suits their model. As a result of this, while every researcher claims to have developed a model that offers superior performance to the alternative methods, this performance was measured in a testing environment directly tailored to the method being assessed.

This variation in the method evaluation indicates that it is very hard to tell which model is superior to the others.

5. Conclusion and Future Recommendations

Link prediction within the context of social networks is by no means a novel research topic. However, the greatest challenge associated with predicting new or missing links in dynamic SNs characterized by ongoing evolution is yet to be adequately addressed.

Table 2: Summary of Famous Link Prediction Methods

No.	LP Strategy	Dataset	Proposed Model (Method)	Features Used	Evaluation and Accuracy Measures	Remarks
[ 64 ]	Probabilistic	Synthetic data A and  B (10,000 nodes each) Robot.Net (2,483,776 nodes) Two biological datasets (Control and Exposure 13,483,584 nodes each) from Stevenson	Deep learning framework (ctRBM) + can quickly learn	Node attributes and network topology	ROC and AUC curves Sum of Absolute Differences (SumD)	Reliable for handling uncleaned data
[ 4 ]	Similarity-based	51 million tweets Twitter reciprocal reply networks over 81 days	Covariance Matrix Adaptation Evolution Strategy (CMA-ES)	Node-specific features and network topological similarities	ROC and AUC	Does not require parametric thresholds. The linearity of the model is one of its weaknesses. Can handle different types of network
[50 ]	Similarity	Irvine Message Enron Email Infectious SocioPatterns News words Nodobo	Integrated Time Series Model (ITM) that combines topological (community and centrality) and temporal information	Network topology, community structure, and node centrality feature	AUC	More realistic for dynamic networks
[ 56 ]	Probabilistic	Two email social network datasets Enron dataset Wroclaw University of Technology	Triad Transition Matrix (TTM) comprising the probabilities of transitions between triads found in the network	Network Local topology observations of the recorded network past information	Compared to preferential attachment (PA) and common neighbors (CN) predictor	Data was pre-processed
[ 55 ]	Maximum likelihood and probabilistic	NIPS co-publication data + synthetic data generated by a model	DSNL model handle change of friendship	Local topologies (represent each entity with a location p in the latent space)	AUC & ROC	Little data with only around 11,000 nodes. Cannot handle large data
[5]	Probabilistic	DBLP and astro-ph of ArXiv.	Graph-based link prediction techniques based on the local probabilistic model	Time-based edge weights derived from temporal aspects	Discounted Cumulative Gain (DCG) and Average Normalized Rank (ANR)	Cannot handle many types of networks
[17]	Temporal Method	Enron E-mail,  Irvine SNS,  Friends and Family SMS	Temporal regularity in interpersonal communication	Node-pair records extraction and time-domain signal generation	Area Under the Curve (AUC)	There is a need to take into consideration the directions of interpersonal communication
[18]	Fuzzy Link	100,000 ratings and 1,300 tag applications	Distance between two different objects	Links among items, fuzzy link importance	MAE and RMSE	There are limitations on the procedure used for evaluating the method
[20]	Temporal Network	Data obtained from (SNAP) Math, Ask, Super, Stack	(Cox PHM), Game theory	Topological features	Average F1Score, Kendall’s Tau Coefficient (KTC)	The first method achieved good accuracy

This paper examines the most current and innovative methods for predicting links in dynamic SNs. Each method explored and discussed in this paper exhibited some sort of good performance, such as accuracy, efficiency, or scalability, in respect of one SN type. A variety of models were explored in this paper. For each explored model, the paper discussed the prediction strategy, the datasets used, the type of features, and the evaluation measures used.

One vital feature of dynamicity concerns the temporal aspects of SNs, which is something that many researchers have considered. Some emerging methods have made great strides in terms of link prediction accuracy and efficiency, including the novel methods that have used different topology and harnessed both supervised and unsupervised techniques. Some methods, such as temporal-based methods, are highly scalable in terms of their ability to predict links [20].

This rigorous analysis of the emerging solutions indicates that there is no one complete method available that predicts emerging or lost links in dynamic social networks to a high degree of accuracy, efficiency, and scalability. Continuous efforts are needed to develop an innovative model that is capable of handling different types of SNs.

Despite the influx of research that aims to predict links in dynamic SNs, we still believe that there is a need for further research to address the problem of the absence of complete research that exhibits high accuracy, high efficiency, and is very scalable as well. Further improvements in accuracy, efficiency, and scalability are very important due to the huge data generated from dynamic SNs.

Conflict of Interest

The authors declare no conflict of interest.

Acknowledgment

The authors would like to acknowledge the assistance and support provided by Ajman university library and United Arab Emirates University library for procuring most of the papers and the books used in this article.

1. Mohammad Marjan, Nazar Zaki, and Elfadil A. Mohamed (2018). “Link Prediction in Dynamic Social Networks: A Literature Review.” IEEE CiSt’18 5^th  Edition International IEEE Congress on Information Science and Technology, Marrakech, Morocco, October 21 – 27, 2018.
2. Wang, P., Xu, B., Wu, Y. and Zhou, X. (2014). Link prediction in social networks: the state-of-the-art. arXiv preprint arXiv:1411.5118.
3. Al Hasan, M. and Zaki, M. J. (2011). A survey of link prediction in social networks. In Social network data analytics(pp. 243–275). Springer US.
4. Bliss, C. A., Frank, M. R., Danforth, C. M. and Dodds, P. S. (2014). An evolutionary algorithm approach to link prediction in dynamic social networks. Journal of Computational Science, 5(5), 750–764.
5. Tylenda, T., Angelova, R. and Bedathur, S. (2009, June). Towards time-aware link prediction in evolving social networks. In Proceedings of the 3rd workshop on social network mining and analysis(p. 9). ACM.
6. Mori J, Kajikawa Y, Kashima H, et al. Machine learning approach for finding business partners and building reciprocal relationships. Expert Systems with Applications, 2012, 39: 10,402–10,407.
7. Wu S., Sun J., Tang J. Patent partner recommendation in enterprise social networks. In: Proceedings of the 6th ACM International Conference on Web Search and Data Mining (WSDM’13), Rome, Italy, 2013. 43–52.
8. Berlusconi G., Calderoni F., Parolini N., Verani M., Piccardi C. (2016). “Link Prediction in Criminal Networks: A Tool for Criminal Intelligence Analysis.” PLOS ONE, DOI:10.1371/journal.pone.0154244, April 22, 2016.
9. Almansoori W., Gao S., Jarada T. N., et al. Link prediction and classification in social networks and its application in healthcare and systems biology. Network Modeling Analysis Health Informatics Bioinformatics, 2012, 1: 27–36.
10. Huang Z., Lin D. K. J. The time-series link prediction problem with applications in communication surveillance. INFORMS Journal on Computing, 2009, 21: 286–303.
11. Li D., Zhang Y., Xu Z., Chu D. and Li S. (2016). “Exploiting Information Diffusion Feature for Link Prediction in Sina Weibo.” Scientific Reports vol(6), article number:  20058(2016).
12. Liu F., Liu B., Sun C., Liu M., and Wang X. (2015). “Deep Belief Network-Based Approaches for Link Prediction in Signed Social Networks.” Entropy, Vol(2015), No(17), PP. 2140-2169; doi:10.3390/e17042140.
13. Zhang H., Wu1 G. and  Ling Q. (2019). “Distributed Stochastic Gradient Descent for Link Prediction in Signed Social Networks.”  Journal on Advances in Signal Processing, (2019) 2019:3. https://doi.org/10.1186/s13634-019-0601-0.
14. Bastami E., Mahabadi A., and Taghizadeh E. (2019). “A gravitation-based link prediction approach in social networks.” Swarm and Evolutionary Computation, 44 (2019), PP. 176–186.
15. Mallek S., Boukhris I., Elouedi Z., and  Lefèvre E. (2018).  “Evidential link prediction in social networks based on structural and social information.”  Journal of Computational Science, 30 (2019), PP. 98–107.
16. Ghazaleh Beigi, Suhas Ranganath, and Huan Liu. (2019). “Signed Link Prediction with Sparse Data: The Role of Personality Information.” In Companion Proceedings of the 2019 World Wide Web Conference (WWW ’19 Companion), May 13–17, 2019, San Francisco, CA, USA. ACM, New York, NY, USA. https://doi.org/10.1145/3308560.3316469.
17. Shinkuma R., Yuki Sugimoto Y., and   Inagaki Y. (2019). “Weighted network graph for interpersonal communication with temporal regularity.” Soft Computing, (2019) 23, PP. 3037–3051.
18. Ai J., Su Z., Li  (2019). “Link prediction based on a spatial distribution model with fuzzy link importance.”  Physica A,  527 (2019) 121155.
19. Aslan S., Kaya B., and Kaya M. (2019). “Predicting potential links by using strengthened projections in evolving bipartite networks.” Physica A, 525 (2019), PP. 998–1011.
20. Bu ,  Wang  Y. ,  Li  H.,  Jiang  J. ,  Wu  Z. , and Cao J. (2019). “Link prediction in temporal networks: Integrating survival analysis and game theory.” Information Sciences, 498 (2019), PP. 41–61.
21. Dharavath R. and Arora  S. (2019). “Spark’s GraphX-based link prediction for social communication using triangle counting.” Social Network Analysis and Mining (2019) 9:28.
22. Eberhard L., Trattner C., and Atzmueller M. (2018). “Predicting trading interactions in an online marketplace through location-based and online social networks.” Information Retrieval Journal, (2018), https://doi.org/10.1007/s10791-018-9336-z.
23. Gao H., Huang J., Cheng Q., Sun H.,  Wang B.,  and  Li  (2019). “Link prediction based on linear dynamical response.” Physica A, 527 (2019), 121397.
24. Golzardi E., Sheikhahmadi ,  and Abdollahpouri A. (2019). “Detection of trust links on social networks using dynamic features.” Physica A, 527 (2019), 121269.
25. Gu S., Chen L.,  Li B.,  Liu W.,  Chen B. (2019). “Link prediction on signed social networks based on latent space mapping.” Applied Intelligence, 2019, https://doi.org/10.1007/s10489-018-1284-1.
26. Jibouni, A., Lotfi, D.,  EL Marraki, M.,   Hammouch, A. (2018). “A novel parameter free approach for link prediction.”  Proceedings – 2018 International Conference on Wireless Networks and Mobile Communications, WINCOM, Marrakesh; Morocco; 16 October 2018 through 19 October 2018.
27. Kumar, A., Singh, S.S., Singh, K., Biswas, B. (2019). “Level-2 node clustering coefficient-based link prediction.”  Applied Intelligence, Volume 49, Issue 7, 15 July 2019, Pages 2762-2779.
28. Dinh, T.N., Nguyen, D.T., and Thai, M.T. (2012) “Cheap, Easy, and Massively Effective Viral Marketing in Social Networks: Truth or Fiction?”, Proceedings of the 23rd ACM Conference on Hypertext and Social Media, June, 2012, pp. 165-174.
29. Monteserin and  Armentano M. G. (2019). “Influence me! Predicting links to influential users.” Information Retrieval Journal, Volume 22, Issue 1-2, 15 April 2019, Pages 32-54.
30. Mutinda W., Nakashima A., Takeuchi  K.,  and Sasaki Y. (2019). “Time Series Link Prediction Using NMF.”  2019 IEEE International Conference on Big Data and Smart Computing, BigComp 2019 – Proceedings1 April 2019, Article number 86795022019 IEEE International Conference on Big Data and Smart Computing, BigComp 2019; Kyoto; Japan; 27 February 2019 through 2 March 2019; Category numberCFP1940X-ART; Code 146803.
31. Wang Z., Liang J.,  and  Li R. (2018). “A fusion probability matrix factorization framework for link prediction.”  Knowledge-Based Systems, 159 (2018), PP. 72–85.
32. Wang ,  Wang  Y.,  Ma  J.,  Li  W.,  Chen N.,  and Zhu  X. (2019). “Link prediction based on weighted synthetical influence of degree and H-index on complex networks.”  Physica A: Statistical Mechanics and its Applications, Volume 527, 1 August 2019, Article number 121184.
33. Wu ,  Shen  J.,  Zhou  B., Zhang X.,  and Huang  B. (2019). “General link prediction with influential node identification.”  Physica A: Statistical Mechanics and its Applications, Volume 523, 1 June 2019, Pages 996-1007.
34. Yuan, W., He, K., Guan, D.,  Zhou, L.,  Li, C. (2019). “Graph kernel based link prediction for signed social networks.” Information Fusion, Volume 46, March 2019, PP. 1-10.
35. Greene, D., Doyle, D. and Cunningham, P. (2010, August). Tracking the evolution of communities in dynamic social networks. In Advances in social networks analysis and mining (ASONAM), 2010 International Conference(pp. 176–183). IEEE.
36. Yao L., Wang L., Pan L., and Yao K. (2016). “Link Prediction Based on Common-Neighbors for Dynamic Social Network.” Procedia Computer Science, Vol (83), 2016, PP. 82 – 89.
37. Liben-Nowell, D. and Kleinberg, J. (2007). The link-prediction problem for social networks. journal of the Association for Information Science and Technology, 58(7), 1,019–1,031.
38. Rossetti G., Guidotti R., Miliou I.,  Pedreschi D., and  Giannotti F. (2016). “A supervised approach for intra-/inter-community interaction prediction in dynamic social networks.” Soc. Netw. Anal. Min. (2016) 6:86, DOI 10.1007/s13278-016-0397-y.
39. Moradabadi, B. and Meybodi, M. R. (2018). Link prediction in weighted social networks using learning automata. Engineering Applications of Artificial Intelligence Journal, 2018, 70: 16–24.
40. Moradabadi, B. and Meybodi, M. R. (2018). Link prediction in stochastic social networks: Learning automata approach. Journal of Computational Science, 2018, 24: 313–328.
41. Wu, Z., Lin, Y., Zhao, Y., Yan, H. (2018). Improving local clustering based top-L link prediction methods via asymmetric link clustering information. Physica A: Statistical Mechanics and its Applications Journal, 2018, 492: 1,859–1,874.
42. Fu, C., Zhao, M., Fan, L., Chen, X., Chen, J., Wu, Z., Xia, Y., Xuan, Q. (2018). Link Weight Prediction Using Supervised Learning Methods and Its Application to Yelp Layered Network. IEEE Transactions on Knowledge and Data Engineering Journal, 2018, 99.
43. Julian, K., & Lu, W. (2016). Application of Machine Learning to Link Prediction.
44. Mohan, A., Venkatesan, R., Pramod, K. V. (2017). A scalable method for link prediction in large real-world networks. Journal of Parallel and Distributed Computing, 2017, 109: 89–101.
45. Caiyan, D., Chen, L., Li, B. (2107). Link prediction in complex network based on modularity. Journal of Soft Computing, 2017, 21(15): 4,197–4,214.
46. Bhat, S. Y. and Abulaish, M. (2015). HOCTracker: Tracking the evolution of hierarchical and overlapping communities in dynamic social networks. IEEE Transactions on Knowledge and Data Engineering, 27(4), 1,019–1,013.
47. Liben-Nowell, D. and Kleinberg, J. (2007). The link-prediction problem for social networks. Journal of the Association for Information Science and Technology, 58(7), 1,019–1,031.
48. Gao, S., Denoyer, L. and Gallinari, P. (2011, October). Temporal link prediction by integrating content and structure information. In Proceedings of the 20th ACM International Conference on Information and Knowledge Management(pp. 1,169–1,174). ACM.
49. Dunlavy, D. M., Kolda, T. G. and Acar, E. (2011). Temporal link prediction using matrix and tensor factorizations. ACM Transactions on Knowledge Discovery from Data (TKDD), 5(2), 10.
50. Ibrahim, N. M. A. and Chen, L. (2015). Link prediction in dynamic social networks by integrating different types of information. Applied Intelligence, 42(4), 738–750.
51. Niladri S., Saptarshi B. , Sukumar N., Sanasam R. S. (2018). Temporal link prediction in multi-relational network. World Wide Web Journal, 2018,  21(2): 395–419.
52. Tabourier L., Libert A-S., and  Lambiotte R. (2016). “Predicting links in ego-networks using temporal information.” EPJ Data Science,  (2016) 5:1, DOI 10.1140/epjds/s13688-015-0062-0.
53. Munasinghe L. and Ichise R. (2012). “Time score: A new feature for link Prediction in Social Networks.” IEICE Trans. Inf. & Syst., Vol(E95-D), No. 3, March 2012, PP. 821-828.
54. Oyama S., Hayashi K., and Kashima H. (2012). “Link Prediction Across Time via Cross-Temporal Locality Preserving Projection.” IEICE Trans. Inf. & Syst., Vol(E95-D), No. 11, November 2012, PP. 2664-2674.
55. Sarkar, P. and Moore, A. W. (2006). Dynamic social network analysis using latent space models. In Advances in Neural Information Processing Systems(pp. 1,145–1,152).
56. Juszczyszyn, K., Musial, K. and Budka, M. (2011, October). Link prediction based on subgraph evolution in dynamic social networks. In Privacy, Security, Risk and Trust (PASSAT) and 2011 IEEE Third International Conference on Social Computing (SocialCom), 2011 IEEE Third International Conference on(pp. 27–34). IEEE.
57. Zaki et al.: Protein complex detection using interaction reliability assessment and weighted clustering coefficient. BMC Bioinformatics 2013 14:163.
58. Chen G. , Xu  ,   Wang J., Feng J.,  Feng J. (2020). “ Robust non-negative matrix factorization for link prediction in complex networks using manifold regularization and sparse learning.” Physica A 539 (2020) 122882.
59. Sarkar, P., Chakrabarti, D. and Jordan, M. (2012). Nonparametric link prediction in dynamic networks. arXiv preprint arXiv:1206.6394.
60. Lü, L. and Zhou, T. (2011). Link prediction in complex networks: A survey. Physica A: statistical mechanics and its applications, 390(6), 1,150–1,170.
61. Virinchi S., Mitra P. (2013). “Link Prediction Using Power Law Clique Distribution and Common Edges Distribution.” In: Maji P., Ghosh A., Murty M.N., Ghosh K., Pal S.K. (eds) Pattern Recognition and Machine Intelligence. PReMI 2013. Lecture Notes in Computer Science, vol 8251. Springer, Berlin, Heidelberg.
62. Dong, L, Li Y.,  Yin H.,  Le H., and  Rui M. (2013). “The Algorithm of Link Prediction on Social Network.” Mathematical Problems in Engineering, Vol(2013), Article ID 125123, 7 pages, http://dx.doi.org/10.1155/2013/125123.
63. Zhang Y., Shen S., and Wu Z. (2018). “Improve Link Prediction Accuracy with Node Attribute Similarities.” International Conference on Computer Engineering and Networks CENet2018 2018: The 8th International Conference on Computer Engineering and Networks (CENet2018), PP. 376-384.
64. T. Riaz, Y. Fan, J. Ahmad, M. A. Khan, and E. M. Ahmed, “Research on the Protection of Hybrid HVDC System,” in 2018 International Conference on Power Generation Systems and Renewable Energy Technologies (PGSRET), 2018, pp. 1–6.
65. Li, X., Du, N., Li, H., Li, K., Gao, J. and Zhang, A. (2014, April). A deep learning approach to link prediction in dynamic networks. In Proceedings of the 2014 SIAM International Conference on Data Mining(pp. 289–297). Society for Industrial and Applied Mathematics.
66. Pan L., Zhou T., Lü L., and Hu C-K. (2016). “Predicting missing links and identifying spurious links via likelihood analysis.” Scientific Reports, Vol(6:22955),  DOI: 10.1038/srep22955.
67. Wu Z., Lin Y., Wan H. and Jamil W. (2016). “Predicting top-L missing links with node and link clustering information in large-scale networks.” Journal of Statistical Mechanics: Theory and Experiment, (2016) 083202.
68. Bhawsar Y. and Thakur G.S. (2016). “Performance Evaluation of Link Prediction Techniques Based on Fuzzy Soft Set and Markov Model.”, Fuzzy Information and Engineering, 8:1, 113-126, DOI: 10.1016/j.fiae.2016.03.007.
69. Menon A.K., Elkan C. (2011) Link Prediction via Matrix Factorization. In: Gunopulos D., Hofmann T., Malerba D., Vazirgiannis M. (eds) Machine Learning and Knowledge Discovery in Databases. ECML PKDD 2011. Lecture Notes in Computer Science, vol 6912. Springer, Berlin, Heidelberg.
70. Han J., M. Kamber, and J. Pei. 2012. Data Mining Concepts and Techniques. Morgan Kaufmann: Waltham, MA 02451, USA, 2012.

(Click Here)

(Click Here)