1. Introduction

This issue has motivated standards such as JPEG2000 to include certain error resilience (ER) techniques and gave rise for the development of joint source-channel techniques dedicated for the AC-encoded data [6, 7]. ER techniques were applied to identify the corrupt segment of the AC codestream. A common method for error detection in arithmetic coding was introduced in [8] where a non zero coding interval is reserved to a non coded symbol called forbidden symbol (FS). While decoding, if the FS is decoded, then an error in the received sequence is indicated. A study on the trade-off between the amount of added redundancy due to the FS and the amount of time required to detect an errors was proposed in [9]. In the works [10, 11], sequential decoding schemes were involved on binary trees and path pruning technique was applied relying on the FS error detection. In [11], Grangetto et al. have modeled arithmetic codes as state machines and a trellis representation for AC code with FS was used in conjunction with the maximum a-posteriori (MAP) decoding algorithm. The authors in [12] proposed a soft input soft output (SISO) arithmetic decoding where a FS-based ER technique was applied and a Chase-like algorithm was slightly modified to provide additional information on the reliability of the decoded bits. Practical implementations on the joint source-channel coding scheme with FS were studied in [13].

The iterative joint source-channel decoding (JSCD) was usually studied by making use of the channel observations and source information to improve the a-posteriori probabilities of each transmitted bit. This can be achieved through the repetitive update and adjustment of a-posteriori and extrinsic information on the one hand and source information on the other hand to achieve a better joint decoding error ratio. In [14], the extrinsic messages in the Turbo decoder are enlarged or reduced by means of the multiplication with a factor which depends on the channel conditions. In [15] channel adaptive plus or minis operations are made to modify the messages in LDPC decoder. Iterative JSCD based on bit flipping algorithms were proposed in [16, 12, 17] where a set of error patterns are generated by identifying the least reliable bits among the decoded sequence. Each test pattern is then checked for correctness by means of a verification code. In this concern, we propose a JSCD algorithm that takes advantage of the error detection capability provided by the FS-based ER technique in the AC decoder to improve the error correction capability of the iterative message passing algorithm (MPA) used for Low Density Parity Check (LDPC) decoding. The iterative decoding procedure offers a convenient way to make use of the source information feedback provided by the ER technique.

In this study, the arithmetic coded sequences of a certain number of image blocks are written line-wise in the so-called read-matrix (RM). In succession, the RM is read column-wise to form the information input sequence of the LDPC encoder. It is worth to note that block partitioning is a common process in the image compression standards, such as in JPEG2000 and H264, and is justified by the average entropy decrease of the image especially when block transformation are employed. For instance discrete the cosine transform is employed in JPEG-XR and HEVC and the discrete wavelet transformation in JPEG2000 and context-based compression algorithm, where the advantage of the correlation between neighboring image blocks is taken. With respect to error resilience, image partitioning is beneficial since error propagation may be prevented.

As a first contribution, the interplay between error detection position and bit reliabilities in the AC input code-stream is discussed and the error probability of each bit positioned before the detected error position is estimated. In this concern, a method for bit back-tracking is proposed which is of great importance in this work. It is worth to note that ACbased error detection is performed in symbol-takt whereas channel decoding is processed in bit-takt, and hence, the feedback information from the AC decoder is transformed in bit-takt.

A second contribution is associated with the proposed approach to JSCD and consists on the way how to involve the estimated bits reliabilities from the AC decoder in the iterative LDPC decoder. The purpose of this approach is to increase the reliabilities of the error-free AC decoded segments and to reduce them in possibly corrupted segments. This is reached by the conditional update of the messages during the iterative process with respect to the AC decoding results. Experimental results have shown that the proposed JSCD scheme outperforms the Tandem decoding and bit-flipping based JSCD schemes in terms of peak signal-to-noise ratio (PSNR), as well as accelerates the iterative MPA process.

The rest of this paper is organized as follows. Section 2 presents the proposed source-channel encoding scheme. In section 3 an overview over the AC is given and the FS-based ER technique is analyzed in terms of bit error probability versus error detection delay. The proposed JSCD scheme is outlined in Section 4. Simulation results are reported in Section 5. Section 6 concludes this paper.

2. Proposed source-channel coding scheme and transmission model

The proposed encoding scheme at the transmitter is depicted in Figure 1. Applying AC over N_B equal size image blocks S₁,··· ,S_NB produces N_B compressed sequences s₁,··· ,s_NB which are written line-wise into the K × L matrix, the socalled read-matrix (RM). The number of image blocks invited to be written in the RM is variable and depends on the RM size, on the image block size and on the AC compression rate for each image block. In order to restrict the zero filling, the block sequences have to be chosen in such a way that the number of not occupied positions in the RM becomes as small as possible. Set partitioning method is applied for this purpose. The sequence resulting from the column-wise reading of the RM is fed into a LDPC systematic encoder. Let c = (c₁,··· ,c_Nc ) be the resulting LDPC codeword where N_c is the codeword length. The code bits of c are mapped into modulated sequence x. For simplicity, we consider a binary phase-shift keying (BPSK) modulation where the m^th modulated symbol in x is given by x_m = (1 − 2c_m),1 ≤ m ≤ N_c. The m^th symbol within the received sequence y can be expressed as

where P is the received signal power at the receiver and n_m is the instantaneous additive noise which is modelled as zeromean Gaussian random variable with variance σ_n². In the sequel, we assume that P is unity. For a BPSK transmission the noise power is E{n²} = σ_n² = BN₀/2, where B is the bandwidth of the passband signal and N₀/2 is the power spectral density per frequency unit of the white Gaussian noise. In addition, we note that the zero forced bit may be not transmitted when assuming the knowledge of the AC coded sequences lengths at the receiver which may re-establishes the zeros at the non-transmitted positions.

For the purpose of the LDPC decoding, supplied by the MPA, the log-likelihood-ratio (LLR) of the m^th estimated code bit, 1 ≤ m ≤ N_c, given the observation y_m at the destination is

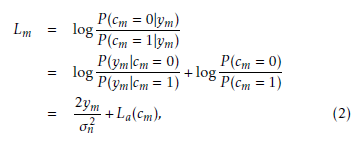where L_a(c_m) is the LLR corresponding to the a-priori information of the m^th estimated code bit.

3. Overview of AC and ER techniques

Let S_b = (S_b,1,…,S_b,NS ) be the b^th image block sequence of N_S symbols from a finite alphabet A = {a₁,··· , a_NA} composed of N_A symbols. Arithmetic coding requires the probability distribution of the input sequence. The interval [0,1) is divided into maximum N_A sub-intervals, each with length equal to the occurrence probability of the alphabet symbols in the sequence S_b. The symbols S_b,1,··· ,S_b,NS are entered symbol by symbol to the arithmetic encoder. Let Low be the lower bound of the interval in which the symbol sequence so far is arranged and Length be the interval length, which is the product of the probabilities of all previous encoded symbols. Low and Length are initialized to 0 and 1, respectively. To encode a symbol from the sequence S_b, corresponding to the i^th symbol in A, both Low and Length must be updated. Low X is refreshed by Low +Length f_b,j and Length is replaced by j=1

Length f_b,i, where f_b,j is the probability of j^th symbol in the alphabet A. After the entire sequence is arranged, it is uniquely specified by any value between Low and High = Low+Length. A number with the shortest binary representation in the interval will be transmitted. The most important advantage of AC is its optimality. AC is optimal in theory and is very nearly optimal in practice. In [18], it was shown that the required bit-size representing S_b is upper bounded by:

where j(S_b,s) corresponds to the position of the symbol S_b,s in A. The major drawback of such algorithm is that the encoding and decoding processes needs an infinite precision machine (values used for Low and High). This drawback was solved in [3], where the authors proposed the use of integer probabilities F_b,i = N_S.f_b,i and scaling techniques. The initial interval [0,1) was substituted by [0,W), where W = 2^{P r} and P r ≥ 2 is the bit precision of the initial interval.

In order to generate incremental output while encoding, the authors in [3] proposed the scaling method where the size of the interval [Low,High) has to be doubled if one of the following conditions holds:

• E₁ : 0 ≤ High < W/2:
  1. Low ←            2 · Low
  2. High ←            2 · High+1
  3. Ouput : 0              followed by           Scale3     ones
  4. Scale3 ←            0
• E₂ : W/2 ≤ Low < W:
  1. Low ←            2 · (Low − W/2)
  2. High ←            2 · (High − W/2)+1
  3. Ouput : 1              followed by           Scale3     zeros
  4. Scale3 ←            0
• E₃ : W/4 ≤ Low < W/2 ≤ High < 3W/4:
  1. Low ←            2 · (Low − W/4)
  2. High ←            2 · (High − W/4)+1
  3. Ouput : no output
  4. Scale3 ←            Scale3+1

Note that Scale3 represents the number of the last E₃ scaling done and is initialized to 0.

3.1         Proposed bit back-tracking within AC decoding with ER technique

The concept of ER technique is usually deployed with AC for the purpose of error detection which can help to reconstruct the corrupted segments of a code-stream. As far as JSCD is concerned, the error propagation properties of AC with the deployed ER technique is worthy studying. An accurate location of the bit errors is generally unachievable when making use of a simple ER technique. AC-based error detection is accomplished in symbol-takt and channel decoding is processed in bit-takt, and hence, the feedback information from the AC decoder should be obviously transformed in bit-takt. This is referred to as bit back-tracking.

We note that the decoding process is similar to the encoding process, and hence the AC decoder will either decode no source symbol or it will decode one or more source symbols for each input bit as described in the encoding process. For the purpose of bit back-tracking, we first define the AC extended encoding/decoding step as follows:

Definition: The AC extended encoding/decoding step is the succession of concluded AC encoding/decoding steps producing at least one output symbol/one output bit with Scale3 is zero or reset to zero.

We note that a concluded AC decoding step is settled when the new subinterval is not entirely within one of the intervals [0,1/2), [1/4,3/4) or [1/2,1). At the t^th extended decoding step, the input bits located in the bit positions range φ_t produce output symbols located in the symbol positions range Φ_t. Up to now, let uˆ _b,t and Sˆ_b,t denote the input bit sequence and the corresponding output symbol sequence at the t^th extended decoding step, respectively. The main idea in the following subsections is that if at least one bit in uˆ _b,t is erroneous, then at least one symbol in Sˆ_b,t is erroneous. For implementation issue a stack can be accessed, where the t^th line contains the tuples (uˆ _b,t,Sˆ_b,t). In order to elucidate the principle of AC extended encoding/decoding step and since encoding and decoding are similar, Table 1 illustrates an example of encoding a sequence S = abaac, where the symbols a, b and c have the occurrence frequencies 20, 10 and 20, respectively, cumulative counts {a,b,c} = {0,20,30,50} and W = 256. The first column is reserved for the extended encoding steps enumerator t.

For instance, at the third extended encoding step, aa and 010 constitute the input symbol sequence and the corresponding output bit sequence, respectively.

3.2         Forbidden symbol technique and error detection delay distribution

Let  be the probability of the FS in the interval [0,1) which is never encoded. The amount of generated redundancy due to the FS is −log₂(1 − ). Decoding the FS at the AC decoder is interpreted as an error detection.

Let ψ_b,p be the event that the FS is first appeared at the p^th symbol position in the b^th AC-decoded sequence and let Sˆ_b,p−_d be the decoded symbol at the (p − d)^th symbol position,

1 ≤ d ≤ p. The joint probability that the (p − d)^th symbol is erroneous and the event ψ_b,p occurs can be expressed by

where S_p−_d is the really transmitted symbol in the finite alphabet set and A_p is a normalization factor which depends on the position p. The probability given in (3) corresponds to the probability that a delay of d symbols is occurred before an error detection at the position p is performed. Thus, d is referred to as error detection delay.

Table 1: AC integer encoding of a sequence abaac with cumulative counts {a,b,c} = {0,20,30,50} and W = 256 showing the extended encoding steps.

t	St	Low	High	ut	Scaling	Scale3
–	–	0	255	–	–	0
1	a	0	101	0 –	E1	0
		0	203		–	0
2	b	81	121	0 1 –	E1	0
		162	243		E2	0
		68	231		–	0
3	a a	68	132	– – 01 0 –	E3	1
		8	137		–	1
		8	59		E1	0
		16	119		E1	0
		32	239		–	0
4	c	156	239	1 –	E2	0
		56	223		–	0

For simplicity, we assume that the occurrence probabilities of the symbols in the alphabet set are near to the forbidden symbol probability. Hence, (3) can be approximately given by the following truncated geometric distribution:

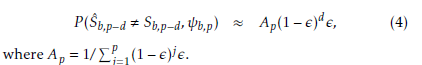The error detection delay distribution in the presence of a FB-based ER technique is investigated. A single bit error is arbitrarily introduced at the input sequence. The number of decoded symbols before decoding the FS is recorded. The probability density functions (PDF) of the error detection delay for two FS probability values, namely  = 0.1 and  = 0.2, are plotted in Figure 2. The finding reveals that the geometric distributions with parameters  = 0.1 and  = 0.2 fit the measured PDFs of the error detection delay.

3.3         Bit error probability estimation from the FSbased ER technique in the AC decoder

In this subsection we intend to determine the error probability of the AC decoder input bits before detecting the FS. Let Sˆ_b,t be the decoding result of the input bit sequence uˆ _b,t at the t^th extended decoding step and let φ_v and Φ_v be the ranges of input bit positions and output symbol positions at the t^th extended decoding step, respectively. Within an extended decoding step, the AC encoding process is a one-toone relationship between the input symbol sequence and the output bit sequence. Accordingly, if the decoded sequence Sˆ_b,t is different from the correct one denoted by S_b,t, then the input bit sequence uˆ _b,φt is certainly erroneous. Hence, the joint probability that the input sequence uˆ _b,t is error prone and the event ψ_b,p occurs can be given by

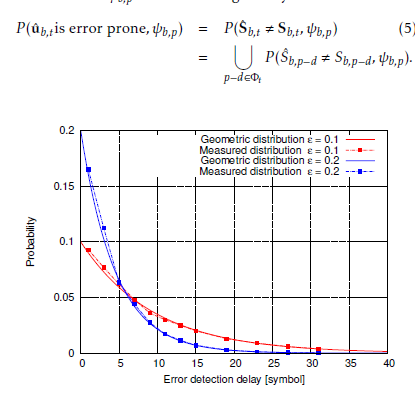Figure 2: PDF of the error detection delay in the presence of a FS-based ER technique and comparison with the geometric distribution in (4) for  = 0.1 and  = 0.2.

Applying the approximation given in (4) and the pointcarre´ formula where all the multiplicative terms are neglected lead to the following approximation:

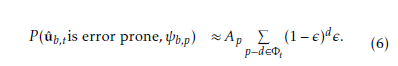Furthermore, the bit error probabilities in the bit range φ_t are assumed to be constant and denoted by P_e,t. This assumption reveals that the probability P (uˆ _b,t is error prone, ψ_b,p) can be approximately given the following expression:

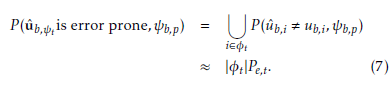where |φ_t| is the size of the bit range φ_t and u_b,i is the correct bit at the input bit position i. From (6) and (7), the error probability of the bits in the input bit range φ_t can be approximately given by

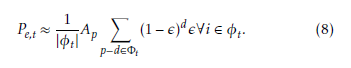The bit error probability given in (8) is calculated within the AC decoding process so as to be involved in the JSCD as shown in the following section.

4. Iterative joint source-channel decoding

Error correction is usually done without taking into account any characteristics of the source data. This is attributable to the Shannon’s well-known source and channel coding separation theory [19]. However, many works in the last decades have shown that considering these two parts jointly can help to enhance the error control performance of the whole system [20, 21].

In the proposed JSCD scheme the information from the ER-based AC decoder, in form of error probabilities of the bits within the corrupted segment, is involved in the decoding process. The main purpose of this strategy is to increase the bit-wise reliabilities of the error-free AC decoded segments and to reduce them in possibly corrupted bit segments. The JSCD scheme is illustrated in Figure 3. The systematic nodes in the Tanner graph correspond to the input bits of the different AC decoders. Let q_vr (0) denotes the message passing from the variable node v to the check node r at the l^th round and represents the probability of c_v = 0 given the channel observation y_v, messages from all check nodes linked to the message node v expect the check node r (r⁰ ∈ C_v\r) and the check equation E_v involving the variable node v.

The corresponding log-likelihood ratio can be expressed by the following expression:

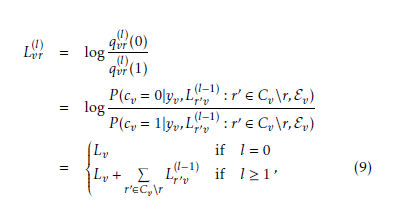where L_v is the LLR of the estimated code bit cˆ_v conditioned

(l−1) on its observed value y_v as given in equation (2), L_r0_v is the the LLR message passed from the check node r⁰ to the variable node v at the (l − 1)^th round that the check equation in r⁰ is satisfied given the code bit c_v and the messages from all variable nodes linked to check node r⁰ except the variable node v (v⁰ ∈ V_r\v). L⁽_r^l₀⁻_v¹⁾ is defined as follows [22]:

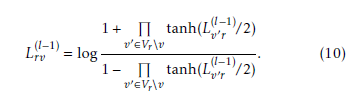The estimated hard code bit cˆ_v at the l^th round is given by

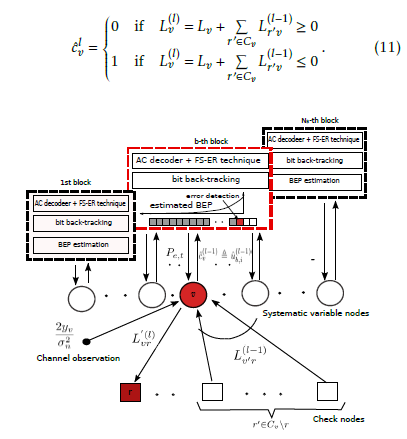Figure 3: Joint Source-Channel Decoding scheme.

The correspondence between the code bit position v and the information bit position i in the b^th input sequence is ensured according to the read write process in the RM. The AC decoder in the b^th block performs error detection using the FS-based ER technique as described above. We distinguish two cases depending on the AC decoding results. The first case holds when AC error-free decoding is performed, in other words no FS is decoded. Let ψ_b,corr be the event when no error is detected while AC decoding of the b^th input sequence at the (l − 1)^th round. For these bits, the message passing from the variable node v to the check node r is modified according to the following expression:

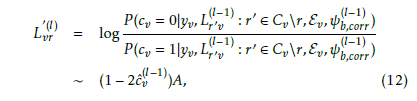where A is a large positive value. These bits in correct decoding passes are now disclosed to the channel decoder, and they can support decoding other undetermined bits involved in the same check equations.

The second case holds when a FS at the position p at the (l − 1)^th round is detected. Let ψ_b,p^(l−1) denotes this event and let Eˆ_b,p denotes the estimated bit-end position corresponding to the detected FS position. At this stage a bit back-tracking effort muss be made to resolve the bit positions from the corresponding symbol position as described in subsection 3.1. The Bit error probability (BEP) of each information bit u_b,i, at the positions i before Eˆ_b,p is estimated according to (8)

(l−1) and is denoted by P_e,t , where t is the extended decoding step corresponding to the bit position i, in other words i ∈ φ_t. No information about the input bits at positions after Eˆ_b,p

(l−1) is provided. The estimated P_e,t corresponds to bit error probability of the systematic variable node c_v. The conventional message L^l_vr passing from the variable node v to the check node r at the l^th iteration is given in (9). The updated message from the variable node v conditioned on the event (l−1) ψ_b,p , which returns due to the independence between the AC decoder input bits to the conditioning on the estimated (l−1) bit error probability P_e,t      , is calculated as follows:

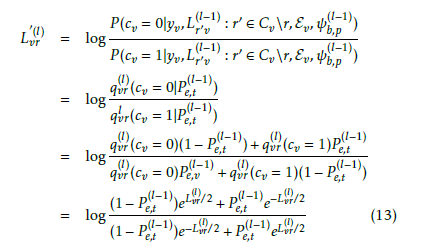Applying the aforementioned change to all bit prior the error detection position could lead to weakening strong bits. To cope with this, it is convenient to limit the reliability change to the most unreliable bits. For this purpose, let Q be the random variable which characterizes the rank of ascending reliabilities L_v in (11) of erroneous bits . For example, Q= 5 means that the fifth least reliable bit is erroneous. Figure 4 shows the distribution of Q for the signal to noise ratio (SNR) levels per source information bit E_b/N₀ = 2,3,4 and 5, and emphasizes that the rank of the most unreliable bits where errors occur is limited by a specific value denoted by Q_L that is considered as a parameter in the decoding process so as to limit the set of modified messages and hence to preserve strong bits. The value of Q_L will be fixed experimentally.

5. Simulation results

In this section we demonstrate the performance of the proposed JSCD scheme. Simulation studies are performed using a LDPC code of length N_c = 40000 and rate 1/2 with parameters (3,6). The outputs of the LDPC encoder are BPSK modulated and transmitted over the additive white Gaussian noise channel. We have tested our JSCD scheme using image block sizes of 16 × 16 and RM size of 200 × 100. The 512 × 512 Washsat image, initially coded at 8 bit per pixel (bpp), compressed at 5.52 bit per pixel (bpp), is considered as test image. Mean-squared error (MSE) values of decoded image are averaged over 1000 independent image transmissions at desired signal to noise ratio level. The average MSE is then converted to PSNR. The absolute value A of the LLRs in (12), corresponding to the segment of bit-streams that do not cause error detection, should be set to arbitrarily high values. In this work the value of A is set to 10. As a consequence, these bits are recognized as very reliable during the subsequent LDPC iteration.

First of all, the aforementioned value Q_L is examined. Q_L is the number of the most unreliable bits where errors occur and is dependent on the the received SNR level per source information bit E_b/N₀ since the absolute value of LLRs become an increasingly significant reliability indicator as SNR increases. Figure 5 shows the PSNR evolution of the proposed JSCD scheme for E_b/N₀ of 1, 2, 3 and 4 dB as a function of Q_L. The figure shows that the best PSNR performance is given for a certain Q_L value. For instance, for E_b/N₀ = 3dB, the best Q_L value is 4. It is worth noting that the higher the SNR level is, the smaller Q_L is.

The performance of the proposed JSCD scheme is compared to that of the Tandem decoding scheme using soft input channel decoding and conventional arithmetic decoding. The PSNRs of the reconstructed images versus E_b/N₀ are illustrated for the two schemes in Figure 6.

Figure 4: Distribution of the rank of ascending reliabilities’ erroneous bits for Eb/N0 = 1,2,3 and 4 dB, .

It is worthy to remark that gains are obtained in terms of average PSNR throughout the SNR per source information bit range. In fact the proposed JSCD scheme exhibits PSNR gains of ∼ 4.5dB, ∼ 8dB and 4.5 dB over the Tandem decoding scheme at the SNRs 2dB, 3dB and 4dB, respectively. The proposed method adds AC decoding operations to each iteration, this can lead to a decoding complexity increase, which is obvious by JSCD subjects. This complexity rise could be balanced out by the suppression of the iteration number. Figure 7 illustrates the mean number of iterations needed for the proposed JSCD scheme as well as for the separated model.

It is obvious that the proposed JSCD system requires less decoder iterations, which means that the required decoding time can be reduced. The decoding iteration number gain can be achieved by as much as 13.8% to 22.18% in the range of E_b/N₀ between 1 and 2 dB.

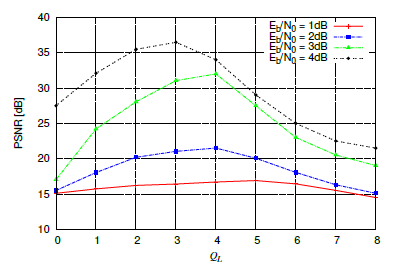Figure 5: Average PSNR evolution versus QL for Eb/N0 = 1,2,3 and 4 dB.

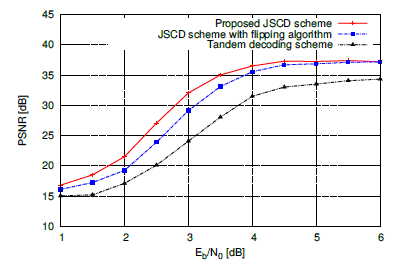Figure 6: Average PSNR evolution versus Eb/N0 of the proposed JSCD scheme with  = 0.2, Tandem decoding scheme and JSCD scheme with bit flipping algorithm.

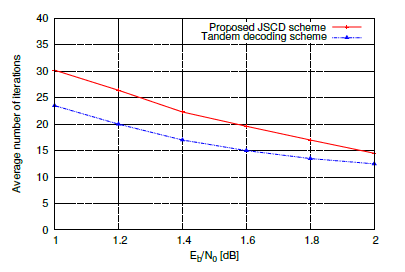Figure 7: Average number of iterations of the proposed JSCD scheme and Tandem decoding scheme.

The results reported in the performed simulations show that the proposed JSCD outperforms standard separated scheme. On the other hand, the optimal choice of the system parameters remains an open issue; in fact, given a channel SNR, the error correction performance depends on the parameters such as FS probability , RM size, image block size. A large value of  means more coding redundancy and assures a faster error detection. The value of  is chosen as a trade-off between coding efficiency and error detection. One could look through simulations for a value achieving the best performance; since analytical performance bounds for the JSCD is very exhaustive. Figure 8 shows that the best JSCD performance is obtained with a value of  = 0.2. In fact, the increase of  from 0 to 0.2 gives a PSNR gain of ∼ 8dB for E_b/N₀ = 3dB. Furthermore, a suitable choice of the RM size could lead to a well distribution of the strong bits over the whole LDPC decoder input sequence. Strong bits could be detected from the correct AC-decoded segments.

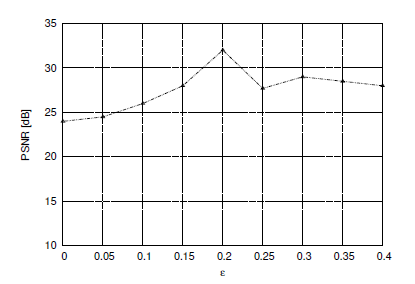Figure 8: Average PSNR versus FS probability  for Eb/N0 = 3dB.

As mentioned in the introduction, we compare the performance of the proposed JSCD scheme with that of the JSCD using the bit flipping algorithm. Such a bit-flipping idea has been used in various joint source-channel decoding approaches as in [16, 12, 17]. It consists on the flipping of the last Q unreliable bits. From these least reliable Q positions, one generate 2^Q − 1 different error patterns. A candidate codeword is given by flipping the non-null bits in the error pattern. If no error detection is verified, the process stops. We note that no image partitioning is carried out during the bit flipping algorithm. A huge number of iterations could arise since 2^Q error patterns must be tested for each image block. To cop with this, a single AC encoding operation was performed on the source message. In this work Q is set to 4 . The results reported in Figure 6 allow us to appreciate the gain offered up to a certain SNR.

6. Conclusion

In this paper, we proposed a JSCD scheme for image transmission. An error resilience technique was applied with AC and the interaction between error detection position and bit reliabilities in the AC input code-stream was discussed. The proposed approach to JSCD incorporates error-free AC-decoder information feedback and error-detection AC-decoder information feedback. In case of corrupted segments, bit backtracking is performed and bits reliabilities are estimated depending on the symbol error position. We have shown how the reliabilities of the bits in the AC decoder input stream are involved in the iterative MPA algorithm. The results show that the proposed scheme at low-to-medium SNRs outperforms the separate source-channel model by approximately 4 to 8 dB with respect to PSNR and reduces the average number of iterations.

Acknowledgment

The authors would like to thank the Deanship of Scientific Research at Jouf University for providing the financial support for publishing this work.

1.  S. Vembu, S. Verdu and Y. Steinberg, ”The source-channel separation theorem revisited” IEEE Transactions on Information Theory, 41(1), 44-54, 1995. DOI: 10.1109/18.370119
2.  J. Rissanen and GG. Langdon, ”Arithmetic coding” IBM Jour- nal of research and development, 23(2), 149-162, 1979. DOI: 10.1147/rd.232.0149
3.  IH. Witten, RM. Neal and JG. Cleary, ”Arithmetic coding for data com- pression” Communications of the ACM, 30(6), 520-540, 1987.
4.  A. Moffat, RM. Neal and IH. Witten, ”Arithmetic coding revisited” ACM Transactions on Information Systems (TOIS), 16(3), 256-294, 1998. DOI: 10.1145/290159.290162
5.  PG. Howard and JS. Vitter, Practical implementations of arithmetic coding In Image and text compression, Springer, Boston, MA, 1992.
6.  I. Moccagatta, S. Soudagar, J. Liang and H. Chen, ”Error-resilient cod- ing in JPEG-2000 and MPEG-4” IEEE Journal on Selected Areas in Communications, 18(6), 899-914, 2000. DOI: 10.1109/49.848245
7.  K. Kamaras, JPEG2000 image compression and error resilience for trans- mission over wireless channels, NAVAL POSTGRADUATE SCHOOL MONTEREY CA, 2002.
8. C. Boyd, JG. Cleary, SA. Irvine, I. Rinsma-Melchert and IH. Witten, ”Integrating error detection into arithmetic coding” IEEE Transactions on Communications, 45(1), 1-3, 2000. DOI: 10.1109/26.554275
9. J. Chou and K. Ramchandran, ”Arithmetic coding-based continuous error detection for efficient ARQ-based image transmission” IEEE Jour- nal on Selected Areas in Communications, 18(6), 861-867, 2000. DOI: 10.1109/49.848240
10. BD. Pettijohn, MW. Hoffman and K. Sayood, ”Joint source/channel coding using arithmetic codes” IEEE Transactions on Communications, 49(5), 826-836, 2001. DOI: 10.1109/26.923806
11. M. Grangetto, P. Cosman and G. Olmo, ”Joint source/channel coding and MAP decoding of arithmetic codes” IEEE Transactions on Commu- nications, 53(6), 1007-1016, 2005. DOI: 10.1109/TCOMM.2005.849690
12. S. Zaibi, A. Zribi, R. Pyndiah and N. Aloui, ”Joint source/channel iterative arithmetic decoding with JPEG 2000 image transmission ap- plication” EURASIP Journal on Advances in Signal Processing, (1), 114, 2012. DOI: 10.1186/1687-6180-2012-114
13. W. Zhang, F. Cen and F. Zhu F, Research on practical implementation of binary arithmetic coding with forbidden symbol for error resilience, In Frontiers in Computer Education, Springer, Berlin, Heidelberg, 2012.
14. Z. Peng, YF. Huang and DJ. Costello, ”Turbo codes for image transmission-a joint channel and source decoding approach” IEEE Jour- nal on Selected Areas in Communications, 18(6), 868-879, 2000. DOI:
    10.1109/49.848241
15. W. Liu and DG. Daut, ”Progressive image transmission based on joint source-channel decoding using adaptive sum-product algorithm” Journal on Image and Video Processing, (1), 18-18, 2007. DOI: 10.1155/2007/69805
16. B. Zheng and S. Gao, ”A soft-output error control method for wire- less video transmission” in 2016 8th IEEE International Conference on Communication Software and Networks (ICCSN), Jun 2016. DOI: 10.1109/ICCSN.2016.7586585
17. T. Tonnellier, C. Leroux, B. Le Gal, B. Gadat, C. Jego C and N. Van Wambeke, ”Lowering the error floor of turbo codes with CRC verifica- tion” IEEE Wireless Communications Letters, 5(4), 404-407, 2016. DOI: 10.1109/LWC.2016.2571283
18. PG. Howard and JS. Vitter, ”Arithmetic coding for data compression”Proceedings of the IEEE, 82(6), 857-865, 1994. DOI: 10.1109/5.286189
19. CE. Shannon, ”A mathematical theory of communication” Bell system technical journal, 27(3), 379-423, 1948. https://doi.org/10.1002/j.1538- 7305.1948.tb01338.x
20. JL. Massey, Joint source and channel coding, MASSACHUSETTS INST OF TECH CAMBRIDGE ELECTRONIC SYSTEMS LAB, Sep 1977.
21.  J. Hagenauer, ”Source-controlled channel decoding” IEEE Transactions on Communications, 43(9), 2449-2457, 1995. DOI: 10.1109/26.412719
22. A. Shokrollahi, LDPC codes: An introduction Digital Fountain, Inc., Tech. Rep, 2003.

(Click Here)

(Click Here)