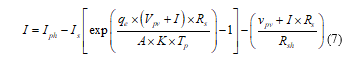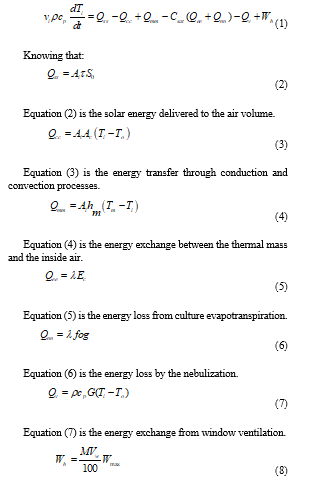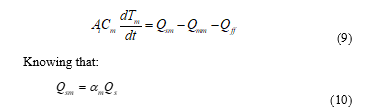1. Introduction

Renewable energies provide an alternative option because they can replace conventional resources in different industrial applications. Renewable energy is a very important factor in greenhouse production. Indeed, a significant amount of energy consumed is required for heating in winter and ventilation in summer. To ensure high quality agricultural production, [1] guarantee an optimum regulation of greenhouse climate in an ecological and energy-saving way. The main purpose of a greenhouse is designed primarily to regulate its indoor climate to optimize crop production and protect plants [2]. The temperature and humidity are regarded both as important control elements [3]. A great deal of research on the control of greenhouse climates was presented in [4].

Some of the causes of the difficulties in controlling greenhouses are the complexity of a physical greenhouse model as well as the relation between the control actions and the processes that will be controlled. Heating, ventilation, humidification and dehumidification systems are designed to regulate the climate inside the greenhouse and to prolong production all year round.

Concerning the importance of indoor temperature and humidity, numerous regulation techniques such as the neural, fuzzy and adaptive regulation for optimizing the greenhouse environment have been used [5-7]. A PI technique was introduced in [8]. A neural network method was developed in [9] for the greenhouse system’s complexity. [10, 11] was designed a regulation of the humidity and temperature in greenhouse by means of the fuzzy logic controller. Description of the Takagi-Sugeno method of air temperature control has been provided in [12]. [13] was based on predictive control.

For the intensive energy consumption in an agricultural greenhouse, it is important to find ways to reduce this consumption. In the following, a contribution to the management of energy consumption in an agricultural greenhouse through a photovoltaic ventilation system is proposed.

In recent years, a rapid development in the industrial uses of DTC technology has been demonstrated. The reasons for this are its rapid torque response, its easiness and robustness in response to changes in rotor parameters. As compared to the vector control diagram, DTC has delivered the same high performance dynamics with a simplified controller design as indicated in [14]. Therefore, we have chosen this method to control the ventilation motor.

The principal aim of this work is to contribute a high-tech control method and to ensure an appropriate greenhouse climate with lower energy consumption. First of all, a photovoltaic system will be developed. In a second step, we will present the greenhouse physical model. Then, we will introduce the fuzzy logic regulator used to control the indoor air temperature and relative humidity. A PV generator system is used to supply the ventilation motor via a DTC control using Matlab/Simulink software.

2. Photovoltaic modelling

Photovoltaic solar energy is an advantageous technology that has several benefits: the availability also in rural areas and the ideal conditions for an environmentally sustainable and efficient greenhouse.

2.1        Photovoltaic panel modelling

A suitable solution for the production of all the power required by the photovoltaic generator.  A Matlab / Simulink modelling of the different parts of the system used. In general, the photovoltaic cell model is generally shown as a simplified circuit model equivalent, as illustrated by Figure 1, the equation is represented as follows [15].

 : Photocurrent independent of  (or ), it is proportional to the incident flux (recombination generation rate) and diffusion lengths of the carriers, so it is linearly dependent on solar radiation and impacted by the temperature according to the following equation:

: the short-circuit current coefficient / temperature

Where  reference temperature, is the actual temperature

S characterize the cell surface irradiation, (1000W/m2 is the nominal irradiation)

: Current flowing through , if is very high, it becomes very low is independent of the voltage, and is given by:

Let us replace in equation (1) equations (3) and (4), the characteristic equation will become:

With:

: The cell ideal factor which can be determined by the recombination mechanisms in the Load zone of space

: is the electron charge (1.6025 x 10~19c)

K: is the Boltzmann constant (1.38 10-23J/K).

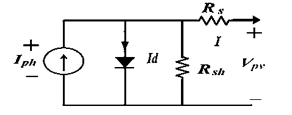Figure 1: Electric model of the PV cell

The PV module configuration (Kaneka D-SA060) is associated in series (4 modules) and placed in parallel (7 modules). Table 1 summarises the photovoltaic generator parameters. [16]:

Table 1: Kaneka GSA060 value parameters

Parameters	Values
Maximum Power	60W (+10/-5%)
Cells per Module	61
Voltage ( )	67V
Current ( )	0.91 A
OC voltage ( )	91.8 V
SC Current ( )	1.19 A
Shunt Resistance	254.8279 ohm
Series Resistance	16.135 ohm

The system studied is composed by the PV generator and the DC-DC converter. DC-DC converter is controlled by the duty cycle generated by MPPT command based on fuzzy method. The variation of solar radiation and outdoor temperature that was measured on March 11th is shown in Figures 2 and 3.

Figure 2: The radiation profile (11/03)

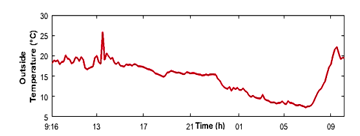Figure 3: The profile of the outside temperature (11/03)

2.2        DC-DC boost converter modelling

The Boost converter is utilized in this task to augment the output voltage in relation to input voltage. Similarly, we also use it follow PPM tracking from the proposed control [17].

With

Figure 4: The electric model of DC-DC boost converter

2.3        Maximum Power Tracking Method

To control a Boost converter, we used the Fuzzy Logic method as this method is very practical and requires fewer measured parameters.

Ø  The Fuzzy Logic controller

This command is designed to track the points of the maximum power. This command has the advantage of being robust. There are three steps considered to define the fuzzy controller concept: the fuzzification, the inference rules and the defuzzification [18], [19].

• The Fuzzification

This phase converts a physical variable into a linguistic variable. For every physical step, there is a degree of membership of a linguistic variable.

• The Rules of inference

This rule determines the controller’s output signal in relation with the signals of input: those are indicated as “IF THEN”. In fuzzy rules, operators “AND”, “OR” intervene. For each rule, which is inserted by “THEN”, the conclusion establishes a link between the membership factors of a premise to the membership function of the output variables.

• The Defuzzification

This step converts fuzzy output ensembles into physical variables suitable for such a process. Numerous defuzzification techniques exist, “centre of gravity” method is selected and described in the following equations:

 : Output value. : Membership degree

• The fuzzification

In this step, we aim at designing a fuzzy controller using Perturb and Observe method.

Input variables are:

Figure 5: linguistic variable Ev (k)

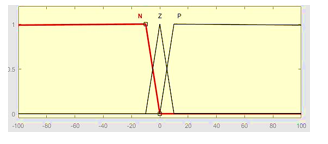Figure 6: linguistic variable Ep (k)

• The inference Rules

The inference rules are described below:

Table 2: Rules of inference

Rules	Ep	Ev	D
1	p	P	z
2	p	N	Gp
3	p	Z	p
4	Z	Z	P
5	Z	N	P
6	z	P	p
7	N	P	Gp
8	N	N	z
9	N	Z	p

• Defuzzification

In Defuzzification we select the “centre of gravity” method that uses a single output variable called duty cycle D.

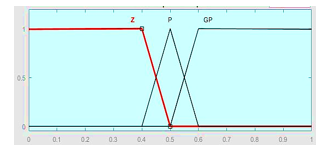Figure 7: The Output of linguistic variable D (k)

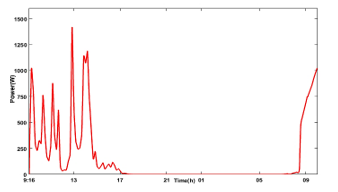Figure 8: Output power supplied by the PV generator

3. Greenhouse Climate Model and Control

3.1.  Model of the greenhouse

Inputs and outputs of a suggested model as shown in the next diagram. Input variables:  the ventilation system,  the heating system and the fogging system, and the measured perturbations of wind speed, solar radiation, outdoor humidity and temperature [20].

The outputs variables: indoor air temperature, the indoor relative humidity.

Figure 9: Model of the Greenhouse climatic [20]

3.2.  Proposed model

·         Heat Balance

In this section, we introduce the dynamic model of air temperature and thermal mass temperature inside greenhouse through the use of equations (1) and (9) [21].

The energy supplied by the heating system is provided by equation (8).

In addition, we describe in (9) the temperature of the thermal mass inside the greenhouse:

Figure 10: Wind speed (11/03)

Figure 11: The outside Humidity (11/03)

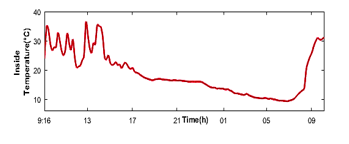Figure 12: The results of the air temperature indoor greenhouse (11/03)

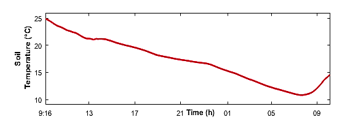Figure 13: The results of the soil temperature indoor greenhouse (11/03)

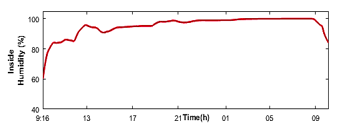Figure 14: The results of the humidity indoor greenhouse (11/03)

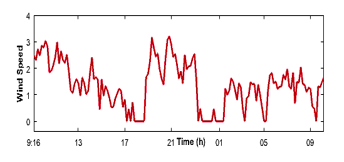
Figure 10 illustrates the wind speed as measured on March 11th, while Figure 11 shows the outdoor humidity as measured on the same date.

Figures 12, 13 and 14 present simulation results for indoor air temperature, inside soil temperature (°C) and humidity (%).

The same greenhouse climate conditions as detailed above in [22] were utilized. That is situated in C.R.T.EN in Tunisia. Greenhouse axes are aligned in parallel with the East-West orientation. Its dimensions are 12.5 metres long, 8 metres wide and 3 metres high.

3.3.  Fuzzy logic controller

Fuzzy logic controller is a sturdy methodology, and its theoretical method of development has been viewed as an interesting solution for a number of different engineering problems. This is thanks to its remarkable properties such as ruggedness, simplicity and flexibility. The fuzzy command is chosen since it is well suitable for multivariable non-linear systems [23, 24]. The methodology is based on three steps: Fuzzification, inference rules and defuzzification [25-27].

The principal purpose of the system is to control the climate inside greenhouse and to enhance its performance.

The fuzzy controller input variables are as follows:

There are three output variables: heating rate (Heating), ventilation rate (Ventilation) and humidification rate (Humidification).

(Heating, ventilation) (Zero, medium, high)

(Humidifier) (Zero, Medium, High)

The fuzzy inference method is the Mamdani or the defuzzification technique used is based on the centre of gravity method.

Figure 15: Membership functions of temperature error ( )

Figure 16: Membership functions of Outside Temperature

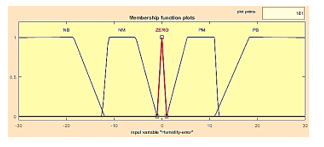Figure 17: Membership functions of humidity error ( )

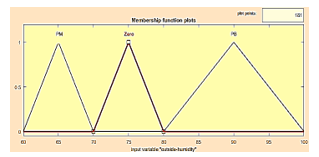Figure 18: Membership functions of the Outside Humidity

Figure 19: Membership functions of the heating rate

Figure 20: Membership functions of the ventilation rate

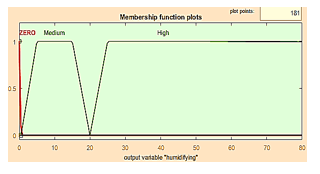Figure 21: Membership functions of humidifying rate

Figures 15, 16, 17 and 18 illustrate the input variables of fuzzy logic regulator.

Figures 19, 20 and 21 present the output variables of fuzzy logic regulator.

4. DTC strategy

The ventilation technique currently used is based on the on-off control [28, 29]. The major disadvantage is high energy consumption. Indeed, at the beginning of the ventilator motor, a large quantity of energy is required to reach maximum speed to reduce the temperature at the desired value. Therefore, using variable speed ventilation rather than the on-off control is more energy efficient.

In this work, a photovoltaic energy ventilation system is proposed, using the DTC direct torque control to regulate the ventilation motor as shown in Figure 22.

We used the DTC to regulate the motor that causes the ventilation. The greenhouse studied is equipped with a ventilation system based on a three-phase asynchronous motor with nominal power (705w)

Both the torque and flow technique can be changed rapidly by adjusting their settings. It also has high dynamic performance, a smaller switching frequency and consequently lower losses. This section focuses on a presentation about the photovoltaic ventilation system. This consists of a three-phase asynchronous motor with a fan as load torque. Such a load can be explained as a quadratic function [30] of motor speed as described in equation (1).

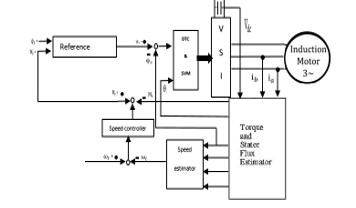Figure 22: The block diagram of DTC for three-phase (IM) drives. SVM: space vector modulation

The DTC method is a technique that is utilized in variable frequency drives in order to regulate both the torque and the speed of three-phase electric motors.

This consists of determining a magnetic flux and motor torque estimate from the measured motor voltage and current. The basic diagrams of DTC Diagram for three-phase asynchronous motors with a speed regulation circuit are displayed in Figure 22.

The torque value is calculated by a proportional integral controller whose equation

ΔW is used to determine the difference between the speed reference and the motor’s actual speed. The ventilation system speed setpoint is coupled to an air flow rate by using the ventilator law through a linear formula specified

5. Simulation and discussion

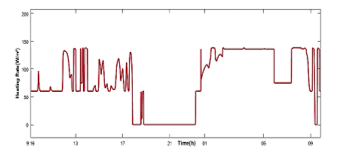
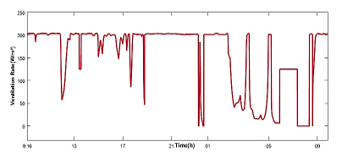
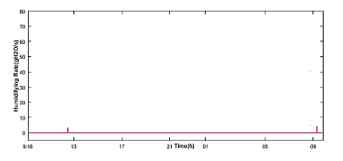
Figure 23 presents the results of the simulation of the fuzzy regulation of the greenhouse air temperature. There are two reference temperatures used as thermal conditions for optimal plant growth: 28°C during the day, 15°C in the night. Simulation results, illustrated in Figure 24, indicate that the humidity is maintained at about 70% of the desired value. Heating, ventilation and humidification rates are shown in Figures 25, 26 and 27 as well.

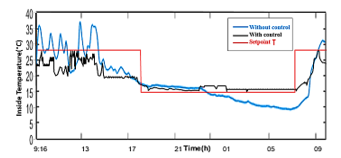Figure 23: Results of greenhouse temperature with the controller Fuzzy Logic (11/03)

Figure 24: Results of greenhouse humidity with the controller Fuzzy Logic (11/03)

Figure 25: MVw [%]

Figure 26: MVα [%]

Figure 27: MVfog [%]

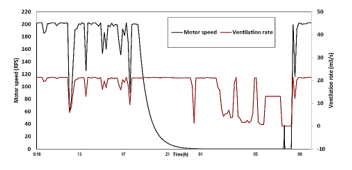Figure 28: The results of ventilation rate and the motor speed

The principal contribution in this document consist on the development of photovoltaic energy to reduce the overloading of the electricity grid. On the basis of this compromise, Variable speed fan is introduced utilizing the (DTC) to support robust control of ventilation rate. Figure 28 illustrates the tracking of the motor speed. The results of the simulation demonstrate that the motor speed responds to the air flow requirements which reveal the robustness of the DTC controller. We observe that when the power delivered by the PVG is not sufficient to ensure the operation of the motor, the speed of the motor is returned to zero, for this purpose, a battery will be used in a future work to stock the energy by day when solar radiation is relatively high.

6. Conclusion

In this work, we presented a model of a PV generator. Then, we developed the greenhouse climate modelling using the fuzzy logic controller to regulate temperature and relative humidity indoor greenhouse. In addition, we studied the DTC regulated ventilation motor, which is powered by a PVG, in order to decrease the overconsumption of energy. The suggested approach to energy conservation has been built on the DTC of the variable speed ventilation motor system supplied by the PVG to ensure robust control. The simulation results show that the power delivered by the PVG, shown in Figure 8, reaches a 1400 Watt when radiation is intense. The power delivered by the PVG is sufficient to ensure the operation of the motor (705 W), as shown in Figure 28. The results achieved in this paper demonstrate the effectiveness of both the fuzzy controller and the DTC control. The suggested system aims to minimize the utilisation of use of the utility of the grid.

Table 3: List of symbols, values and units

A	Windows area [50m²]
A	Constant for the renewal of the volumetric flow
Ac	Conduction and convection loss coefficient
Ai	Greenhouse area [100m²]
Cm	Heat capacity of the thermal mass
Cp	Heat capacity of the air [1003J Kg-1 °C-1]
Csat	Air saturation value
Di	Water vapor deficit in air
Ec	Evapotranspiration of crops
fogg	Water flow rate of fogging system
Fvv	Water rate in the air change flow
G	Renewal air flow
gwb	Boundary-layer conductance
gws	Stomatal conductance
hm	Coefficient of conductivity between air and thermal mass
Hi	Indoor relative humidity
Ho	Outdoor relative humidity
L	Leaves area index
MVfog	Fogging system manipulated variable
MVw	Variable for adjusting the heating system
MVα	Variable manipulated for opening windows
psat	Pressure of saturation
p	Pressure in the atmosphere [98.1 kPa]
Qcc	Conduction energy exchange and convection phenomena
Qee	Evapotranspiration of crops causes energy loss
Qff	Ground energy loss
Qmm	Exchange of energy with thermal mass
Qnn	Nebulization energy loss
Qss	Solar energy provided to the air volume
Qsm	Energy absorbed by the thermal mass by daytime
Qv	Energy exchange through window ventilation
Rn	Crop absorbs solar radiation
So	Solar radiation
Ti	Indoor temperature
Tm	Temperature of thermal mass
To	Outdoor temperature
Tref	Soil temperature at reference depth
Vi	Volume of the greenhouse [300m3]
V	Wind speed
Wh	Heating system energy
Wmax	Heating system maximum power
Xi	Absolute indoor humidity
Xo	Absolute outdoor humidity
Xsat	Absolute saturation humidity
Xsat	Absolute saturation humidity
Zref	Reference depth
α	Window opening angle
Δ	Water vapour saturation slope
γ	The psychometric constant
λ	Latent heat of vaporization
ρ	Air density [1.25 Kgair m-3]
Τ	Greenhouse transmission coefficient

1.  E. Fabrizio, 2012, Energy reduction measures in agricultural greenhouses heating: Envelope, systems and solar energy collection, Energy and Buildings, 53, 57-63.
2.  H. Challa, E.M. Nederhoff, G.P.A. Bot, and N.J. van de Brack, Greenhouse climate control in the nineties, Acta Horticulturae: 230 (1988), pp. 459-470.
3.  B.J. Bailey, and I. Seginer, Optimum control of greenhouse heating Acta Horticulturae, 245 (1989), pp. 512-518.
4.  Y. Hashimoto, Recent strategies of optimal growth regulations by the speaking plant concept Acta Hort., 260 (1989), pp. 115-122.
5.  Hahn, F.: Fuzzy controller decreases tomato cracking in greenhouses. Comput. Elect. Agric. 77, 21–27 (2011).
6.  Ferreira, P.M.; Faria, E.A.; Ruano, A.E.: Neural network models in greenhouse air temperature prediction. Neurocomputing 4, 51– 75 (2002)
7. Rodríguez, F.; Guzmán, J.L.; Berenguel, M.; Arahal, M.R.: Adaptive hierarchical control of greenhouse crop production. Int. J. Adapt. Control Signal Process. 22, 180–197 (2008)
8. A.J. Udink ten Cate, Modeling and (adaptive) control of greenhouse climates. Ph.D thesis. Agricultural University of Wageningen, 1983.
9. X. Luan, P. Shi, X. Luan, P. Shi, and F. Liu, “Robust adaptive control for greenhouse climate using neural networks,” Int. J. Robust Nonlin Control, vol. 21, no. 7, pp. 815–826, 2011.
10.  M. Azaza, K. Echaieb, F. Tadeo, E. Fabrizio, A. Iqbal, and A. Mami, “Fuzzy decoupling control of greenhouse climate,” Arab J Sci Eng [2015] 40:2805-2812, 2015.
11. P. Salgado and J. B. Cunha, “Greenhouse climate hierarchical fuzzy modelling,” Control Eng. Pract., vol. 13, no. 5, pp. 613–628, May 2005.
12. M. nachidi, F. Rodriguez, F. Tadeo, and J.L. Guzman, “Takagi-sugeno control of nocturnal temperature in greenhouses using air heating,” ISA Transaction 50 [2011] 315-320, 2011.
13. M. E. Ghoumari, H. J. Tantau, and J. Serrano, “Non-linear constrained MPC: Real-time implementation of greenhouse air temperature control,” Comput. Electron. Agric., vol. 49, no. 3, pp. 345–356, 2005.
14. A. L. Mohamadein, R. Hamdy and Shady M. Gadoue, “A Comparison Between Two Direct Torque Control Strategies For Flux And Torque Ripple Reduction For Induction Motors Drives”, Proceedings of the Ninth International Middle East Power Systems Conference (MEPCON’2003), Shebeen Al-Koum, Egypt, December 2003, 16-18.
15. M. G. Villalva, J. R. Gazoli, and E. R. Filho, “Comprehensive Approach to Modeling and Simulation of Photovoltaic Arrays,” Power Electronics, IEEE Transactions on, vol. 24, 2009, pp. 1198-1208.
16.  M. JOMAA, M. Yassine Allani, F.TADEO, and Abdelkader Mami, Design and control of the hybrid system PV-Wind connected to the DC load, 9th International Renewable Energy Congress (IREC), 2018, 10.1109/IREC.2018.8362515.
17. V. Salas, E. Olıas, A. Barrado, A. Lazaro, “Review of the maximum power point tracking algorithms for standalone photovoltaic systems”. Solar Energy Materials & Solar Cells (2006); 90:1555–1578.
18.  H. Othmani, D. Mezghani, A. Belaid, A. Mami,” New Approach of Incremental Conductance Algorithm for Maximum Power Point Tracking Based on Fuzzy Logic”, International Journal of Grid and Distributed Computing Vol. 9, No. 7 (2016), pp.121-132. 2016.
19.  Hegazy Rezk, and Ali M. Eltamaly, A comprehensive comparison of different MPPT techniques for photovoltaic systems, Solar Energy, February 2015, Vol. 112:1-11.
20. M. Jomaa, F. Tadeo and A. Mami, “Modelling and control of greenhouses powered by a renewable energy system,” 2017 18th International Conference on Sciences and Techniques of Automatic Control and Computer Engineering [STA], Monastir, 2017, pp. 482-487.
21. X. Blasco, M. Martinez, J. M. Herrero, C. Ramos, and J. Sanchis, “Model-based predictive control of greenhouse climate for reducing energy and water consumption,” Computers and Electronics in Agriculture 55, 2007, 49-70.
22.  M. Abbes, A. Farhat, A. Mami, and G. Dauphin-Tanguy, “Pseudo bond graph model of coupled heat and mass transfers in a plastic tunnel greenhouse,” simulation modelling practice and theory 18, 2010, 1327-1341, 2010.
23.  Bennis, N.; Duplaix, J.; Enéa, G.; Haloua, M.; Youlal, H.: Greenhouse climate modelling and robust control. Comput. Electron.Agric. 61, 96–107 (2008)
24. Iliev, L.; Zakeri, A.; Sazdov, P.; Baytelieva, A.M.: A fuzzy logic based approach for integrated control of protected cultivation. World Appl. Sci. J. 24, 561–569 (2013)
25.  R. C. Miranda, E. V. Ramos, R. Peniche-Vera, and G. Herrera-Ruiz, “Fuzzy Greenhouse Climate Control System based on a Field Programmable Gate Array,” Biosystems Engineering, 2006, 94, 165-177.
26.  Dayan, mulation and control of ventilation rates in greenhouses. Mathematics and Computers in Simulation, 3-17, 2004.
27.  S. Z. Hassan, H. Li, T. Kamal, F. Mehmood, “Fuzzy embedded MPPT modeling and control of PV system in a hybrid power system” 12th International IEEE Conference on Emerging Technologies (ICET) 18-19-October 2016
28. S. Z. Hassan, H. Li, T. Kamal, M. Q. Abbas, M. A. Khan and G. M. Mufti, “An Intelligent Pitch Angle Control of Wind Turbine”, 2017 IEEE International Symposium on Recent Advance on Electrical Engineering (RAEE’17), Institute of Engineering and Applied Sciences, Islamabad, Pakistan from October 24-26, 2017.
29. Villarreal, Simulated performance of a greenhouse cooling control strategy with natural ventilation and fog cooling. Biosystems Engineering, 217–228, 2012.
30.  J. Chen, Estimation of motor startup speed profile using low-resolution timing signals and motor speed-torque curve, In 20th International Compressor Engineering Conference, Purdue, Paper 1808, 2010.

(Click Here)

(Click Here)