1. Introduction

This paper is an extension of work presented initially in 2018 15th International Computer Conference on Wavelet Active Media Technology and Information Processing (ICCWAMTIP) [1]. Control of pH neutralization in the chemical and biotechnological industries is a typical process [2]. The pH of this effluent must be retained within environmental boundaries, before discharging the effluent streams from wastewater treatment plants. Tight pH control is also critically required in pharmaceutical production. However, owing to the high nonlinearity of the pH process, robust and high performance pH process control is often difficult to obtain [3-5]. The process gain of these processes can differ from a small range of pH values to several orders of magnitude. Thus it can exhibit severe static nonlinear behavior.

So far, many authors have proposed, developed, and implemented different control techniques to overcome this problem. The classical PID controller is the first technique applied to control the pH [6-8]. In the field of industrial applications, the PID controller is considered as the most popular controller types, but it has been unable to satisfy the growing demand for efficiency, speed, and accuracy. Nonlinear control techniques also have been applied [9-21]. Other works involve intelligent control technique [22, 23]. In general, most of the above methods require an adequate model, which could not be easy to obtain, add to that the complexity of the controller design based on the above approaches. Hence, pH neutralization process requires a new approach to control it.

In [24-26], Han introduced the powerful control technique active disturbance rejection control (ADRC) and simplified and identified in [27]. The states and disturbance can be estimated in the ADRC before an error can occur, which can ultimately attain early compensation and disturbance resistance. Since it was introduced, the ADRC method has gained worldwide attention and broad implementation and has become common after its linear form has appeared [28]. In many fields, ADRC has been implemented effectively, benefiting from its full control characteristics as fast system response, large scale adaptation, and small overshoot [29].

In this technique, a unique state observer is used to estimate what is called total disturbance. The uncertainties in the dynamics of the internal process and the disturbances of the output are considered as total disturbances. This observer is called the extended state observer (ESO), and it can track the state-space model’s extended state, which can achieve this goal. The plant’s state-space model should include only the model estimate. A linear model in a state-space form may be an estimate for a nonlinear system [29].

This work proposes a different control technique based on estimating the disturbances and actively rejecting it for pH neutralization process. All the disturbances typically presented in pH process are lumped together in one signal called total disturbances. The extended state observer tracks these disturbances and the control law cancels it.

The organization of this paper is as follows. The pH process’s model is given in section 2. Section 3 briefly presents the technique of feedback linearization. Section 4 shows the ADRC control system for the pH process. Section 5 gives the simulation results, and section 6 gives a general conclusion.

2. Model of pH Process

Figure 1 shows a schematic diagram describing the pH process. The process consists of an acid flow rate (q₁), buffer flow rate (q₂), and the base flow rate (q₃) mixed in the tank. pH₄ represents the output of the process, where q₃ represents the control input. By using the conservation equations of the reaction invariants and equilibrium relations, a dynamic model has been derived. Set tank volume (V), Ideal mixing, constant density, and full ion solubility are considered as assumptions for modeling. The system’s chemical reactions are:

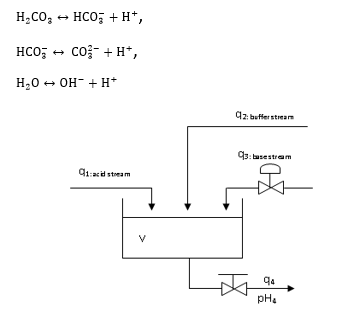Figure 1: The process of pH neutralization

The reaction’s equilibrium constants are

The chemical balance is formed using the reaction invariant concept [30]. The invariants concentrations are (i=1,2,3,4):

where  is a charge-related quantity, and  is the carbonate ion concentration, and they are independent of the extent of the reaction. The concentration of the hydrogen ion is calculated from:

The hydrogen ion  with the following relationship calculates the pH of the effluent stream:

The dynamic model is given by the vessel’s material balance:

This put the process model in a state-space form as

Note that Eq. (1) is linear in  and the unknown parameters are presented in the vector . The relation between the state variables  and the output  is nonlinear as shown by

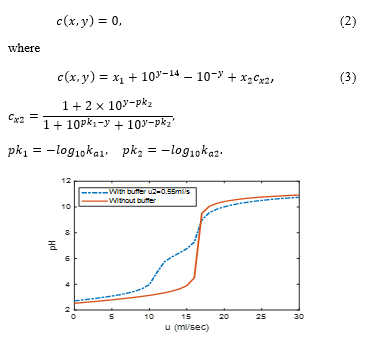Figure 2: The dynamics of the pH process

Table 1 shows the nominal values of the parameters.

Table 1. Model Parameters Nominal Values

Parameter	Nominal value
	2900 ml
	0.003 M HNO3
	M H2CO3
	0.03 M NaHCO3
	0.003 M NaOH
	M NaHCO3
	16.6 ml/s
	0.55 ml/s
	15.8 ml/s
	7.00
	0.003 M
	M
	-0.03 M
	0.03 M
	M
	M
	M
	M

Figure 2 shows the static dynamics of the pH process, which shows strong nonlinearity.

3. Feedback Linearization Technique

For the severely nonlinear system expressed in (1-3), a nonlinear controller based on feedback linearization (FL) technique is first designed.

Consider the following nonlinear system

The objective is to find a linear differential relation between a new input  and the output . The system has a relative degree  if

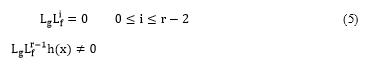where Lf in the direction of  f is the Lie derivative. Suppose the system above has a relative degree of  and is linearizable, then the input transformation

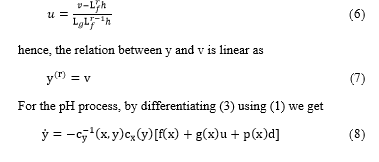
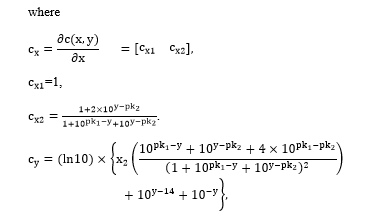Since  for all  and  of interest, the relative degree  and the linearization relation is

Now, assume  is the output of a PID controller in the form

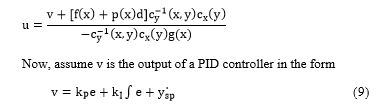where  and  is the reference signal,  is the proportional gain,

The control structure of the FL controller is shown in Figure 3.

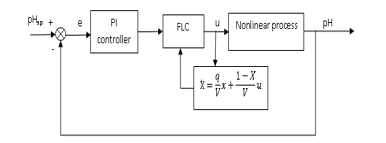Figure 3: The control structure of the FL controller

4. ADRC Solution for the pH Process

It is shown that the control structure using the feedback linearization method is very complicated. To simplify the control design, ADRC is designed. It is shown that all the nonlinear and time-varying terms under ADRC are components of the total disturbance that need to be estimated and rejected, making the design and structure much more straightforward.

4.1.  Conventional linear ADRC

We can rewrite the system described in (1) as

where  is the total disturbance, and  is the coefficient of the output change rate to the control variable step and varies all through the process. Now, ADRC task is to estimate f in real time and cancel it in the control law, which putting the extended state observer as a choice tool from the modern control theory. Define the cases as  and , where the extended state is represented by ; then, Eq. (10) rewritten as

Here  is the controller gain and  is the reference signal.

The structure of the ADRC is shown in Figure 4.

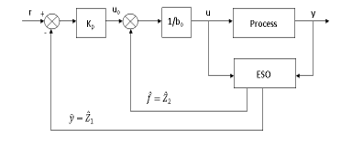Figure 4: ADRC structure for a first-order process

The gains of the observer are chosen as   and  to put the observer poles at . In the same way, the controller gains are selected as  to put the pole of the control loop at    and  are called the observer bandwidth and controller bandwidth, respectively.

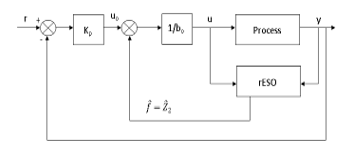Figure 5: ESO based reduced-order ADRC

4.2.  Reduced-order  ADRC (rADRC)

In the ADRC, a second-order ESO is used to obtain the extended state compensation estimate; however, redundancy occurs when the state’s first component can be directly measured [31]. A reduced-order state observer is employed, as shown in Figure 5.

The state observer of reduced-order for  is

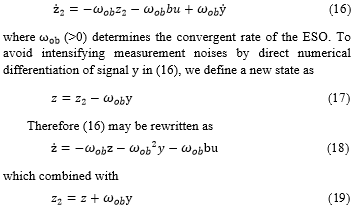constitutes the reduced-order ESO. The remaining controller design is the same as those above.

5. Simulation Results

A comparison between the performances of the designed FL and ADRC controllers is carried out through simulation. The change in buffer and feed stream flow rate is regarded as a disturbance to the system and shown in Fig. 6. The ADRC parameters are shown in Table 2.

Table 2. ADRC controller parameters

ADRC
rADRC

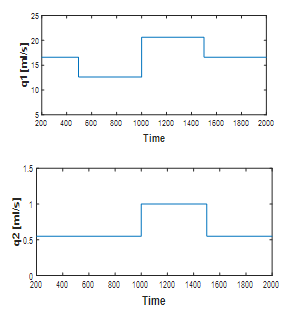Figure 6: The change of buffer and feed stream flow rate

There are two cases considered in this simulation.

A.       Constant Parameters

First, let us look at the case of the constant parameter. The efficiency of both disturbance rejection (Figure 7) and setpoint tracking (Figure 8) is examined to evaluate the effectiveness and robustness of the control system. A comparison to the FL controller carried out to illustrate the advantages of the ADRC as well as the rADRC. It can be observed from Figure 7 the superiority of ADRC and rADRC over the FL controller. We can see from Figure 8 that ADRC tracks the change in setpoint very well, and rADRC tracks it even better, while the FL controller shows some overshoot with longer settling time.

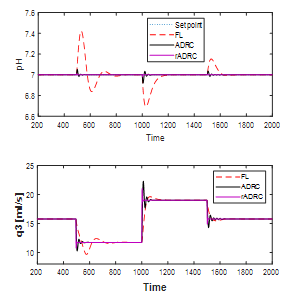Figure 7: The performance of disturbance rejection

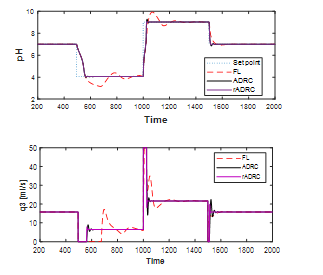Figure 8: The performance of setpoint tracking

B.       Variations in the parameters

The parameters changes are discussed In this case. They are regarded and handled as a system’s internal disturbance. Figure 9 shows the changes in the concentrations of the feed stream.

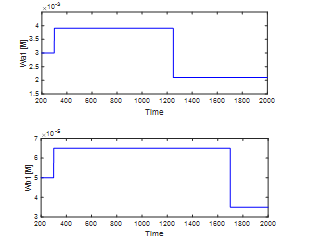Figure 9: Variations in the concentration of the feed stream

Figure 10 shows the performance of the disturbance rejection, while Figure 11 shows the performance of the setpoint tracking. We can see obviously that ADRC and rADRC are superior to the FL controller.

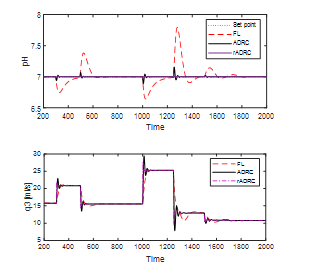Figure 10: The performance of disturbance rejection with variation in parameters

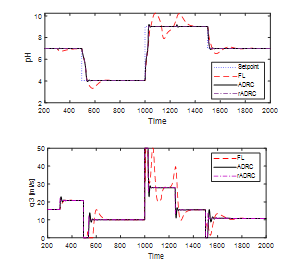Figure 11: The performance of setpoint tracking with variation in parameters

6. Conclusion

A novel control technique (ADRC) for a pH process is presented in this paper. ADRC is an excellent solution to the process that needs a high performance controller to overcome the modeling errors and disturbances. ADRC’s pH simulation studies showed a major enhancement over nonlinear FL control. For more analysis, a reduced-order ADRC was designed and proved that it has the most significant performance in regulating the pH in the existence of the input and external disturbances. The ADRC method is a strong algorithm, particularly in rejection of disturbances. Compared to FL control technique, design and tuning are much more straightforward.

Conflict of Interest

The authors declare no conflict of interest.

1. M. H. Eljack, M. B. Musa, W. Tan, “pH Neutralization Process Control Using Linear Active Disturbance Rejection Control.” In 2018 IEEE 15th International Computer Conference on Wavelet Active Media Technology and Information Processing (ICCWAMTIP). 205-210, 2018. https://doi.org/10.1109/iccwamtip.2018.8632617
2.  M. A. Henson, D. E. Seborg, “Adaptive nonlinear control of a pH neutralization process,” IEEE transactions on control systems technology, 2(3), 169-182, 1994. https://doi.org/10.1109/87.317975
3.  F. G. Shinskey, pH and PION Confro1 in Process and Waste Streams.New York: Wiley, 1973. https://doi.org/10.1016/0013-9327(74)90073-1
4.  G. K. McMillan, pH Control. Research Triangle Park, NC: Instrument Society of America, 1984.
5.  A. Johnson, “The control of fed-batch fermentation processes-A survey,” Automatica, 23(6): 691-705, 1987. https://doi.org/10.1016/0005-1098(87)90026-4
6. R. A. Aguiar, I. C. Franco, F. Leonardi, & F. Lima. Fractional PID Controller Applied to a Chemical Plant with Level and pH Control. Chemical Product and Process Modeling, 13(4), 2018. https://doi.org/10.1515/cppm-2018-0004
7.  R. Vilanova, A. Visioli, PID Control in the Third Millennium: Lessons Learned and New Approaches”, Springer, London 2012.
8. R. A. Wright, C. Kravaris, “Nonlinear pH control in a CSTR,” American Control Conference Proceeding, 1540-1544, 1989. https://doi.org/10.23919/acc.1989.4790431
9. T. K. Gustafsson, K. V. Waller, “Dynamic modeling and reaction invariant control of pH,” Chem. Eng. Sci. 38(3): 389-398, 1983. https://doi.org/10.1016/0009-2509(83)80157-2
10. P. Jutilia, “An application of adaptive pH-control algorithms based on physio-chemical modeling in a chemical waste-water treatment plant,” Int. J. Control. 38(3): 639-655,1983. https://doi.org/10.1080/00207178308933099
11.  G. Pajunen, “Comparison of linear and nonlinear adaptive control of pH-process,” in Proc. IEEE Control Systems Magazine. 7(1): 39-43, 1987. https://doi.org/10.1109/mcs.1987.1105238
12. J. R. Panish, C. B. Brosilow, “Nonlinear inferential control,” AIChE J., 34(4): 633-644, 1988.
13. W. C. Li and L. T. Biegler, “Newton-type controllers for constrained nonlinear processes with uncertainty,” Ind. Eng. Chem. Res., 29(8): 1647-1657, 1990. https://doi.org/10.1021/ie00104a012
14. G. L. Williams, R. R. Rhinehart, J. B. Riggs, “In-line process model-based control of wastewater pH using dual base injection,” Ind. Eng. Chem. Res., 29(7): 1254-1259, 1990. https://doi.org/10.1021/ie00057a029
15. J. J. E. Slotine, W. Li, Applied Nonlinear Control, 2nd ed., Prentice Hall, Inc., Upper Saddle River, NJ, 1991.
16. M. H. E. Elameen, M. N. Karsiti, & R. Ibrahim, “Nonlinear model feedback linearization control strategy of a pH neutralization process,” In 2014 5th International Conference on Intelligent and Advanced Systems (ICIAS) (pp. 1-5). IEEE, 20014. https://doi.org/10.1109/icias.2014.6869488
17.  S. F. Graebe, M. M. Seron, G. C. Goodwin, “Nonlinear tracking and input disturbance rejection with application to pH control,” Journal of Process Control, 6(2-3): 195–202, 1996. https://doi.org/10.1016/0959-1524(96)86054-9
18.  H. Degachi, W. Chagra, & M. Ksouri. “Nonlinear model predictive control for pH neutralization process based on SOMA algorithm.” INTERNATIONAL JOURNAL OF ADVANCED COMPUTER SCIENCE AND APPLICATIONS, 9(1), 391-398, 2018. https://doi.org/10.14569/ijacsa.2018.090153
19.  A. W. Hermansson & S. Syafiie. “Model predictive control of pH neutralization processes: a review.” Control Engineering Practice, 45, 98-109, 2015. https://doi.org/10.1016/j.conengprac.2015.09.005
20. J. Chen, Z. Liu, Y. Peng, Q. Guo, “A New Control Method in pH Neutralization Process.” Springer, Berlin, 511-519, 2013. https://doi.org/10.1007/978-3-642-38524-7_56
21. A. Grancharova, J. Kocijan, & T. A. Johansen, “Explicit output-feedback nonlinear predictive control based on black-box models,” Engineering Applications of Artificial Intelligence, 24(2), 388-397, 2011. https://doi.org/10.1016/j.engappai.2010.10.009
22.  M. Heredia-Molinero, J. Sanchez-Prieto, J. Briongos, M. Palancar, “Feedback PID-like fuzzy controller for pH regulatory control near the equivalence point,” J. Process Control, 2014, 24(7): 1023–1037. https://doi.org/10.1016/j.jprocont.2014.05.006
23.  M. H. Dolatabadi, M. N. Monfared, A. Fakharian, “Robust H-infinity control for the pH neutralization process based on fuzzy models.” In: Fuzzy Systems (IFSC), 13th Iranian Conference on, IEEE, 1–6, 2013. https://doi.org/10.1109/ifsc.2013.6675681
24. J. Q. Han, “Auto-disturbances-rejection controller and its Application, Control and Decision,” January, 13(1): 19–23, 1998. (In Chinese).
25. J. Q. Han, “From PID Technique to Active Disturbances Rejection Control Technique,” Control Engineering of China, 9(3): 13–18, March 2002. https://doi.org/10.1109/tie.2008.2011621
26. J. Q. Han., “Active Disturbance Rejection Control Technique – the technique for estimating and compensating the uncertainties,” National Defense Industry Press, 197-270, 2008.
27. Z. Gao, “Scaling and parameterization based controller tuning,” Proceedings of the American Control Conference, Denver, 6: 4989-4996, 2003. https://doi.org/10.1109/acc.2003.1242516
28. Z. Chen, Y. Wang, M. Sun, & Q. Sun, “Convergence and stability analysis of active disturbance rejection control for first-order nonlinear dynamic systems,” Transactions of the Institute of Measurement and Control, 41(7), 2064-2076, 2018. https://doi.org/10.1177/0142331218794812
29.  J. Ping & B. Wang. “Development of User-defined Block Library for Active-Disturbance-Rejection-Control,” In 2010 Third International Conference on Information and Computing, Vol. 2, pp. 151-154, 2010. IEEE. https://doi.org/10.1109/icic.2010.132
30. K. V. Walker, P. M. Makila, “Chemical reaction invariants and variants and their use in reactor modelling, simulation, and control,” Ind. Eng. Chem. Process Des. Dev., 20(1): 1-11, 1981. https://doi.org/10.1021/i200012a001
31.  R. Yang, M. Sun, Z. Chen, “Active disturbance rejection control on the first-order plant.” Journal of Systems Engineering and Electronics, 22(1): 95-102, 2011. https://doi.org/10.3969/j.issn.1004-4132.2011.01.012

(Click Here)

(Click Here)