1. Introduction

This workpaper is an extension of work originally presented in´ IEEE 2018 Open Innovations Conference (OI) [1], as a contribution on developing software to determine the behavior of photovoltaic arrays, e.g. [2, 3], in order to be able to size correctly a deployment in any cases: residential, commercial, industrial and even farming interesting works based in two-diode model simulation [4] – [9] use Matlab to evaluate the performing of photovoltaic arrays. However, this work shows the results of an alternative computational system, based on two-diode model used for polycrystalline silicon PV cells [10]– [13], that determines the performance of a cell under sunlight irradiance variations and hence the relevance of knowing the efficiency of the device under study. To achieve this goal, the behavior of a semiconductor in sunlight conditions have been considered as well as temperature changes, to determine the current density between the terminals of the cell, generally consisting of a n-type and p-type semiconductor materials, which are brought togheter in the well-known n-p junction. The current of carriers under the photovoltaic phenomenon are deduced by means of the equations that describe the physical model that lead us to a nonlinear equations system, which will be solved by software using different Scilab functions. The coefficients of equations have been determined through the most important parameters of any photovoltaic array: short-circuit current (I_sc), open-circuit voltage (V_oc), maximum current (I_max) and voltage (V_max), all of them determined experimentally in Photonic Laboratory of Cendit. Once the equations are solved, the I-V and P-V curves of the array under test are obtained, and they are compared with the results obtained using Matlab and the solar simulator facility from one manufacturer of the module under study. However, the results obtained include the performance of the DC-AC current inverter, which is part of the system, using a complete bridge configuration, PWM controller and LC filtering at the output. The computer system developed shows not only the I-V and P-V curves of the device under test but also shows the efficiency and the filling factor of whole set.

This workpaper was developed in five sections: Physical and Mathematical Modeling to focuses phenomena and equations according with the photovoltaic arrays used; Experimental Setup to describe the procedures performed in the laboratory to obtain the data required; Software Development with the scope of describe the tools used and the programming developed, as well as the use of the obtained experimental data; Results and Conclusions to analyze, compare, discuss and verify the operation of the computational tool presented.

2. Physical and Mathematical Modelling

The physical properties of a commercial photovoltaic array made of polycrystalline silicon was considered in this case, constituted by a n-p junction of semiconductor materials under the physical fundamentals of cells of this type described in [14, 15]. Isolated, each semiconductor material retains its neutral charge. The holes are the majority carriers in the p-type material and their positive charge is compensated by negatively-charged ionized acceptor atoms, while the electrons are the majority carriers in the n-type material where there is a large concentration of free electrons compensated by positively-charged ionized donor atoms. If both semiconductor materials are placed together, a very large difference in electron concentration occurs that causes an hole diffusion current from p-type material towards the n-type material as well as an electron diffusion current from the n-type material through the metallurgical junction to the p-type material, but the region close to the junction become free of mobile charge carriers, reason why this area is denoted as a depletion or space-charge region. The diffusion generates minority carriers in each region. The gradual depletion of the charge carriers generates a charge zone made up of acceptors and donor atoms, which is no longer compensated by the free mobile carriers. As quasi-neutral regions are denoted the regions around of the depletion zone, where the neutral charge is maintained (see figures 1 and 2).

In the depletion region, under equilibrium conditions and darkness, an internal electric field is formed which forces the charge carriers to move in the opposite direction to the concentration gradient, therefore, the diffusion current continues its flow, while the forces act on the charge carriers, compensate each other, then the diffusion and drift (due to the internal electric field created around the junction) currents that originate from the carriers are compensated, reason why the net current density is zero (I_drift = I_{dif fusion}). When an increase in temperature occurs, electron-hole pairs are generated, provided that thermal energy can undo the bonds, increasing the minority carriers within the material, which causes a current density due to thermal-generation.

Figure 1: n-p junction (top: before junction).

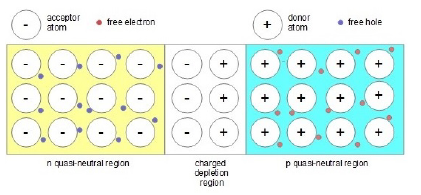Figure 2: n-p junction (after junction).

The difussion currents (due to minority carriers) into n-type and p-type materials causes recombination currents since the minority carriers recombine with the majority carriers (the electron-hole pairs are undone). The recombination current is compensated by the thermal-generation current (I_rec = I_gen). The recombination strongly determines the performance of the photovoltaic cell, since the current that can be collected by the minority carriers within the semiconductor is reduced.

When the thermal equilibrium is broken, under illumination conditions, due to photons with enough energy (and frequency) to create an electron-hole pair, between the valence and conduction bands of the metallurgical junction, which increases the concentration of the minority carriers, is enabled the flow of holes from the n-type region to the p-type region, and vice versa in the case of the electrons. The flow of the photo-generated carriers determines a photo-generation current density (of intensity I_ph), which is added to the current density by thermal generation when the temperature increases within the material.

Based on the above, the behavior of the photovoltaic cell in darkness can be described as a currents balance due to recombinations and thermal generation phenomena, by 1:

where I₀₁ and I₀₂ are the saturation current in the quasi-neutral

regions and the saturation current in the depletion region, respectively, q is the carrier’s charge, k is the Boltzman’s constant, T is the temperature, V is the built potential due internal electric field in the junction, A is the ideality factor between both regions. In this case, note that the exponential function is like the Boltzman Approximation, which has been demonstrated in the literature.

On the other hand, under illumination condition, the photogeneration current I_ph appears as shown in expression 2:

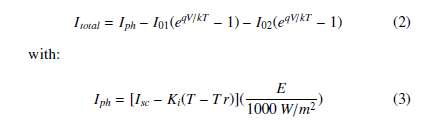where I_sc represents the short-circuit current, I_total corresponds

to carriers net flow between the conducting terminals from the photovoltaic array, K_i is the short-circuit current coefficient, T_r represents the reference temperature and E is the irradiance.

The I-V and P-V curves, current-voltage and power-voltage respectively, can be obtained from equation (2), whose performance is shown in figure 3, where the I_sc is pointed at the left extreme when V = 0 and V_oc in the right extreme at I_total = 0.

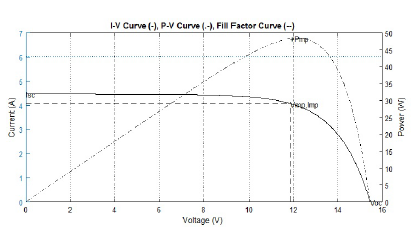Figure 3: I-V Curve (blue), P-V Curve (red) and Fill Factor (yellow).

When the short-circuit condition is given, I_max not could be reached completly, in fact is a little lower due to the high resistivity presents between the ends of the junction, equivalent to a resistance in parallel to the current source and the diodes, denoted as shunt resistance (R_sh). In the other side, when the open-circuit condition is given the V_max not could be reached due to the ohmic losses in the union of the contacts with the ends of the n-p junction, denoted as resistance in series (R_s) to the current source and diodes.

The behavior of a single photovoltaic cell is given by the combination in parallel or series of a single photovoltaic cell, modifying expression (4) by the following:

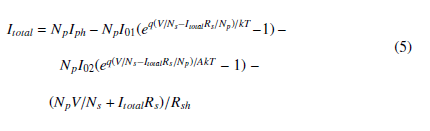
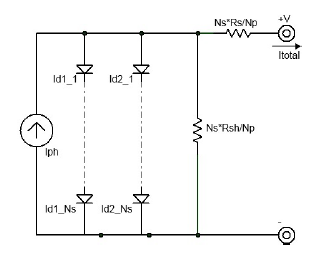Figure 4: Equivalent circuit for a photovoltaic array.

where I_ph is represented by a current source and the current under darkness (I₀₁ and I₀₂) by two diodes in parallel, justifying the ideal factor between both diodes denoted as A, N_p and N_s, are the number of cells (from the array) in parallel or series , respectively.

The equivalent circuit to (5) is shown in Figure 4.

Using the short-circuit condition, V = 0 gives I_total = I_sc, then:

Finally, to determine the values of I₀₁, I₀₂, R_s, R_sh, A, has been solved the equations system given by (8), (10), (11), (12), with the following conditions that regards the device under test:

3. Experimental Setup

The values of V_oc, I_sc, V_max and I_max for the photovoltaic array setup in laboratory, were acquired from I-V curves gives via experimental, under controlled temperature and solar levels, making the necessary measurements and following what is indicated by flow diagram shown in figure 5.

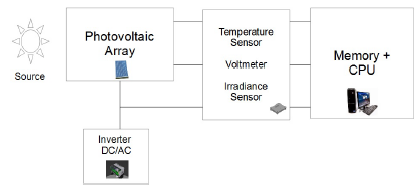Figure 5: Flow diagram of experimental setup.

In fact, this data was acquired using a device developed in the laboratory based on PIC 18F2550, which has enough memory capacity to operate an SD memory card for data storage, as well as an RS485 interface for trasmission in real time to a computer. The device was based on the scheme proposed in [16]. The device is constituted by three sensors:

• A photodiode to measure the solar irradiance, using the BPW31. – A temperature sensor, using the LM35.
• A voltmeter, using the ADC PIC module.

To calibrate the solar irradiance sensor, the TES 1333 was used, while for the temperature the infrared thermometer IDEAL 6165 and the multimeter Fluke 179 were used. For the acquisition of data, a script was generated in SCILAB to obtain the data via serial port, in order to plot in real time, for known conditions of irradiance (W/m2) and temperature (^o C), I-V curves using a variable load variable (max. 10 A). The figures 6 and 7 show some photos about the experimental setup.

Figure 6: Captures of experimental setup (UNERVEN array).

Figure 7: Captures of experimental setup (SIMENS array).

The technical specifications of photovoltaic (PV) module under test are indicated in table 1: Power (Max.), Voltage (Nominal), Series Cells (Ns) and Parallel Cells (Np).

Table 1: PV arrays under test (both polycrystalline).

Parameter	UNERVEN MSF	SIEMENS PC-2-JF
Power	195 W	35 W
Voltage	24 V	17 V
Ns	48	36
Np	1	1

The I-V curves for several solar irradiance levels during the useful solar day for each model of photovoltaic module under test are shown in figures 8 and 9.

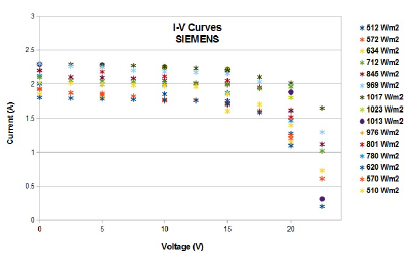Figure 8: I-V experimental curves for UNERVEN SMF.

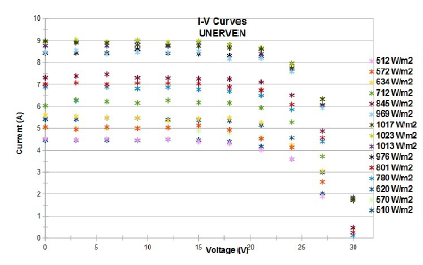Figure 9: I-V experimental curves for SIEMENS PC-2-JF.

Table 2 shows the values obtained in laboratory for parameters:

V_oc, I_sc, V_max and I_max, from photovoltaic arrays under test.

Table 2: Experimental values obtained.

Parameter	UNERVEN	SIEMENS
Voc	30.25 V	23.18 V
Isc	8.72 A	2.41 A
Vm	23.76 V	2.12 A
Im	8.15 A	17.49 V

4. Software Development

A SCILAB script was developed to solve nonlinear equations system constituted by expressions (8), (10), (11), (12), using the function fsolve [x₀, F], with x₀ defined as a vector with the initial values and F defined as a vector that describes equations mentioned before.

First of all, we have to define the equations to solve as a function:

function[f] = F(x)

kB = value; q = value; T = value; Voc = value; Isc = value;

Vm = value; Im = value;

Vt = value;

Rsh = value;

f(1)      =                   x(1) ∗ (exp(Voc/Vt) − exp(Isc ∗ x(4)/Vt)) + x(2) ∗

(exp(Voc/(x(3) ∗ Vt)) − exp(Isc ∗ x(4)/(x(3) ∗ Vt))) − Isc + (Voc − Isc ∗ x(4))/Rsh; f(2) = −x(4) ∗ ((x(1)/Vt) ∗ exp(Voc/Vt) + x(2)/(x(3) ∗ Vt) ∗

exp(Voc/(x(3) ∗ Vt)) + 1/Rsh) − 1;

f(3) = x(1) ∗ (exp(Voc/Vt) − exp((Vm + Im ∗ x(4))/Vt)) + x(2) ∗

(exp(Voc/(x(3)∗Vt))−exp((Vm+Im∗ x(4))/(x(3)∗Vt)))+(Voc− Vm)/Rsh − Im ∗ (1 + x(4)/Rsh); f(4) = −x(4)∗((x(1)/Vt)∗exp(Isc∗ x(4)/Vt)+(x(2)/(x(3)∗Vt))∗

exp(Isc ∗ x(4)/(x(3) ∗ Vt)) + 1/Rsh) − 1; end function

Then, we have to define a script to solve the equations:

x0 = [min_value; scale_f actor;max_value]; y = f solve(x0, F); I1 = y(1);

I2 = y(2);

A = y(3);

Rs = y(4);

The expression defined by (5) is a trascendental equation that was solved in this case using Xcos from Scilab. Figure 10 shows how the four terms in (5) are determined. For more details see [1].

In the last blocks a DC-AC converter has been included and using a full-bridge configuration and a LC filter in the out, with PWM control. For more details in [1].

The I-V and P-V curves generated in Scilab, under Standard Test Conditions (STC) from the mathematical two-diodes model used for each array under test: SIEMENS and UNERVEN, are shown in figures 11 and 12.

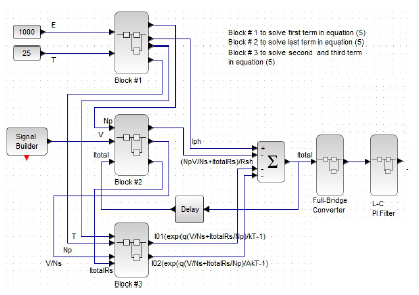Figure 10: Xcos solution to simulate photovoltaic arrays with DC/AC inverter.

Figure 11: I-V and P-V curves through Scilab (PV array: UNERVEN).

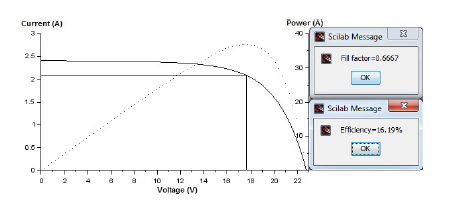Figure 12: I-V and P-V curves through Scilab (PV array: SIEMENS).

5. Results

The I-V curves from different sources are shown in Figures 13 and 14: Solar Simulator (from UNERVEN, class A), Matlab Simulator (based on [1]) and Scilab Simulator, for each photovoltaic array under study on STC (1000 W/m² , 25 ^oC). The solid line and the dash-dotted line are very close to each other, even if some approximation algorithm was not used to solve the equations of two-diode model as in recent workpapers cited above.

The I-V curves for several solar irradiation levels using Xcos from Scilab for each photovoltaic array under study are shown in Figures 15 and 16. Again, the solid line and the dash-dotted line are very close to each other, with an accuracy superior to 99.9 percent.

6. Conclusions

A computational tool has been put to test in laboratory, based on a free software platform, which allows evaluate in real time the efficiency not only of a photovoltaic array, but also the effects generated by a DC-AC inverter coupled like a load to the system as in real enviroment, using in the develop the physic models cited. Test were coducted in two commercial photovoltaic arrays, and aditionally, the performance results were compared with other tools (licensed) reaching a high accurate.

In contrast with experimental tools used (Solar Simulator Class

A from UNERVEN) and computational tool based on Matlab, using Scilab (free software) was improve the perfomance of photovoltaic arrays, even a real time estimation of fill factor and electrical efficiency as an additional feature respect to works cited above. works.

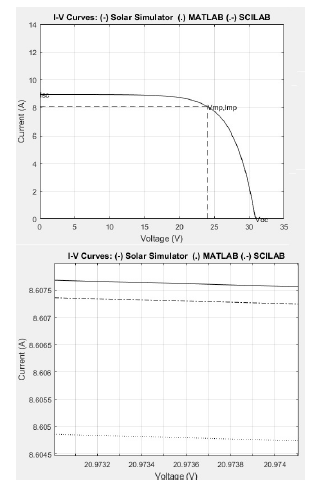Figure 13: I-V Curves: Solar Simulator, Matlab, Scilab (PV array: UNERVEN).

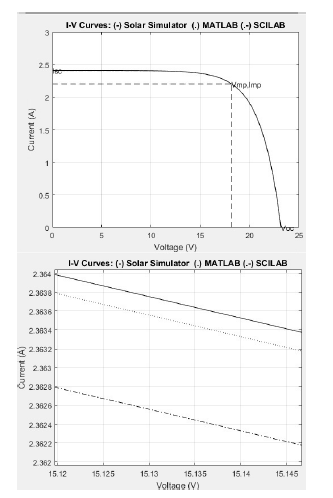Figure 14: I-V Curves: Solar Simulator, Matlab, Scilab (PV array: SIEMENS).

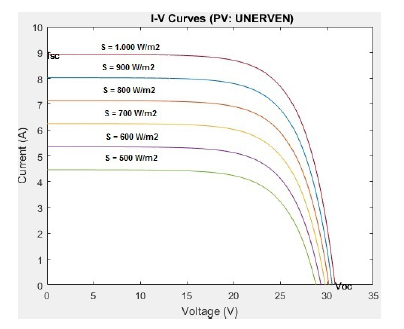Figure 15: I-V Curves: for several irradiation levels (PV array: UNERVEN).

Figure 16: I-V Curves: for several irradiation levels (PV array: SIEMENS).

Conflict of Interest

The authors declare no conflict of interest.

Acknowledgment

The authors would like to thank to Ministerio del Poder Popular para Ciencia y Tecnolog´ıa, Ministerio del Poder Popular para la Energ´ıa Electrica, Unerven – PDVSA Industrial, pro-´ fessors Humberto Rojas and Carlos Rojas from Facultad de Ciencias de la U.C.V.

1.  H. L. Nu´n˜ez Ram´irez, G. G. Carvalho Kassar, F. C. Brito Maestre, Y. I.Gamboa Maldonado, L. A. Santos Avendan˜o, C. Gavidia Toro,“Highly Ac- curate and Inexpensive Computational Tool for Improving Photovoltaic Ar- rays Performance and Efficiency Measures” in Proceedings of the IEEE
   2018 Open Innovations Conference (OI), Johannesburg, South Africa, 2018. https://doi.org/10.1109/OI.2018.8535899
2. S. Chowdhury, S. P. Chowdhury, G. A. Taylor, and Y. H. Song, “Mod- elling, simulation, performance analysis of a PV array in an embed- ded environment”, in Proceedings of the 42nd International Univer- sities Power Engineering Conference (UPEC), , Brighton, UK, 2007. https://doi.org/10.1109/UPEC.2007.4469048
3.  K. Ishaque, Z. Salam, and H. Taheri, “Simple, fast and accurate two-diode model for photovoltaic modules” Solar Energy Materials and Solar Cells, vol. 95(2), 586-594, 2011. https://doi.org/10.1016/j.solmat.2010.09.023
4. N. Hashim and Z. Salam,“Critical evaluation of soft computing methods for maximum power point tracking algorithms of photovoltaic systems” IJPEDS,10(1), 548-561, 2019. https://doi.org/10.11591/ijpeds.v10.i1.pp548- 561
5. A. Hemza, H. Abdeslam, C. Rachid and N. Aouan,“Simplified meth- ods for evaluating the degradation of photovoltaic module andmod- eling considering partial shading” Measurement, 138, 217-224, 2019. https://doi.org/10.1016/j.measurement.2019.01.098
6. P. A. Gbadega and A. K. Saha, “Effects and Performance Indicators Eval- uation of PV Array Topologies on PV Systems Operation Under Partial Shading Conditions”, in Proceeding of the 2019 Southern African Univer- sities Power Engineering Conference, Bloemfontein, South Africa, 2019. https://doi.org/10.1109/RoboMech.2019.8704823
7. T. Ma, W. Gu, L. Shen and M. Li,“An improved and comprehensive mathe- matical model for solar photovoltaic modules under real operating conditions”Energy, 184, 292-304, 2019. https://doi.org/10.1016/j.solener.2019.03.089
8. P. Ranjan Satpathy, R. Sharma and S. Dash,“An efficient SD-PAR technique for maximum power generation frommodules of partially shaded PV arrays” Solar Energy, 175, 182-194, 2019. https://doi.org/10.1016/j.energy.2019.03.078
9.  G. Sai Krishna and T. Moger, “Improved SuDoKu reconfiguration technique for total-cross-tied PV array to enhace maximun power under partial shading conditions” Renewable and Sustainable Energy Reviews, 109, 333-348, 2019. https://doi.org/10.1016/j.rser.2019.04.037
10.  M. Wolf, G. J. Noel, R. J. Stirn, “Investigation of the double exponential in the current-voltage characteristics of silicon solar cells” IEEE Trans. Electron Devices, 24(4), 419-428, 1977. https://doi.org/10.1109/T-ED.1977.18750
11.  D. S. H. Chan and J. C. H. Phang, “Analytical Methods for the Extraction of Solar Cell Single- and Double-Diode Model Parameters” IEEE Trans. Electron Devices, 34(2), 286-293, 1987. https://doi.org/10.1109/T-ED.1987.22920
12. N. Veissid, A. M. De Andrade, “The I-V silicon solar cell characteristic temper- ature dependence an experimental study using the standard deviation method”, in Proceedings of the 10th European Solar Photovoltaic Energy Conference,
    Lisbon, Portugal, 1991. https://doi.org/10.1007/978-94-011-3622-8 11
13. A. Gow, C. D. Manning, “Development of a model for photovoltaic ar- rays suitable for use in simulation studies of solar energy conversion systems”, in Proceeding of the 1996 Sixth International Conference on Power Electronics and Variable Speed Drives, Nottingham, UK, 1996. https://doi.org/10.1049/cp:199608909.03.089
14. Luque, S. Hegedus, Handbook of Photovoltaic Science and Engineering. Wil- ley, 2nd Edition, 2011.
15. A. Smets, K. Ja¨ger, O. Isabella, R. van Swaaij, M. Zeman, Solar Energy- he Physics and Engineering of Photovoltaic Conversion, Technologies and Systems. UIT Cambridge, 2016.
16.  M. A. Mart´inez, J. M. Andu´jar and J.M Enrique, “A New and Inexpensive Pyranometer for the Visible Spectral Range” Sensors, 9(6), 4615-4634, 2009. https://doi.org/10.3390 15

(Click Here)

(Click Here)