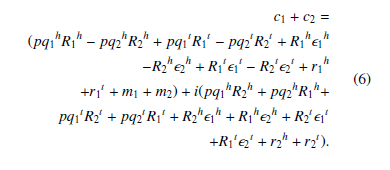1. Introduction

An encryption scheme is said to be FH, if it allows to perform addition and multiplication operations explicitly over the cipher-texts while performing implicitly the same operations over the plaintexts. This new type of ciphering is very required in cloud systems mainly when users treat the cloud as a third untrusted party. With Homomorphic Encryption (HE) the cloud is able to process over encrypted storage and the privacy of the user is preserved at the cloud side. In Figure. 1, we show the case of a mobile user sending an encrypted query to the cloud using HE, thus the cloud is able to process encrypted query over encrypted data to return an encrypted answer. The user can do the decryption.

The notion of homomorphism was first introduced by Rivest, Adleman and Dertouzo [1] as privacy homomorphism after the invention of RSA crypto-system [2]. The basic RSA crypto-system is a multiplicative homomorphic scheme that allows to perform multiplication operations over the cipher-texts. Give, for example, RSA public key, p_k = (N,e) and cipher c_i = (m_i)^emod(N) for a plain-text m_i. It is simple to demonstrate that ^Q_i c_i = (^Q_i m_i)^emod(N). Several works followed the RSA scheme. A state of art of HE is given in [3] – [6]. Some of the known homomorphic schemes are: Paillier cryptosystem [7, 8], Domingo Ferrer crypto-system [9, 10] which is a HE scheme based on polynomial calculations. The Enhanced MORE [11] is another FHE based on matrix calculation and the NOHE [12] scheme is a lightweight FHE that profits from the simplicity and the homomorphic behavior of logic NOT. The most valued work in this domain was given by Craig Gentry in his Ph.D. thesis in 2009 [13, 14]. The work of Gentry was inspired from lattice based cryptography. Gentry first introduced a SHE scheme that supports a bounded number of operations over the cipher-texts. Then he developed a new refresh mechanism called Bootstrapping [15] – [19] to make the scheme FH and supports unbounded operations. An important FHE scheme is the BGV crypto-system developed by Brakerski, Gentry and Vaikuntanathan in [20, 21]. Since BGV scheme is also Somewhat Homomorphic (SH), Modulus Switching (MS) is a technique used with BGV to extend the circuit’s depth during the evaluation procedure.

In this paper, our main motivation is to add a value in homomorphic encryption by designing a new simple and robust FHE based on simple complex numbers operations . We first build a new asymmetric SHE complex-based scheme, then we apply Gentry refresh mechanism (Bootstrapping). In comparison with BGV which is lattice based encryption, our scheme is simply based on complex addition and multiplication operations. In addition, Bootstrapping supports unbounded number of circuit depth in our scheme, while MS extends the BGV evaluation to a limited number.

The rest of the paper is organized as follows: in section 2, we present the basic concept of HE with the properties that can lead to a HE scheme. In section 3, we introduce our new FHE scheme built using complex numbers theory. In section 4 we consider our implementations for the new Complex-based scheme and the

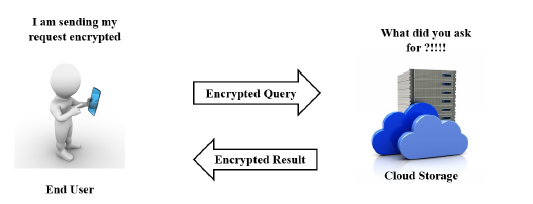Figure 1: Cloud Scenarion Under Homomorphic Encryption

BGV scheme under Python using SAGEMath Library, followed by a crypt-analysis of our new scheme based on the Approximate GCD problem [22, 23, 24]. And finally the conclusion, comparison between the two schemes and future works are listed in section 5.

2. Homomorphic Encryption

In this work, we focus on asymmetric schemes. Consider an asymmetric scheme α, where p_k is the public key, s_k is the secret key, c_i is the ciphered text of a plain-text m_i. A homomorphic scheme has 3 different basic functions that are: KeyGen_α that generates (p_k, s_k), Encrypt_α(p_k,m_i) that outputs cipher-text c_i, Decrypt_α(s_k,c_i) that outputs the plain-text m_i.

2.1     Evaluation Function

In addition to the three basic functions listed above, a homomorphic scheme has also an evaluation function defined by Evaluate_α that takes as input the public key p_k, a circuit L and a tuple of ciphertexts C = (c₁,c₂,c₃,….,c_t), cipher of the input plain-texts vector (m₁,m₂,…,m_t). The evaluation function outputs a cipher-text Ψ given by:

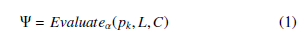2.2    Homomorphic Properties

When the circuit L performs a certain operation over the encrypted data as written in 1, the cloud is computing a predefined Boolean function f that can be written in a polynomial form. A polynomial form is a set of addition and multiplication gates. Thus to build a HE scheme we should satisfy these two basic properties:

1. Addition

2. Multiplication

where m₁ and m₂ are two plain-texts in {0,1} and Enc_α(p_k,m_i) is the encryption function.

3. Homomorphic Complex Scheme

In this section, we build our scheme using complex numbers. We first list the security parameters and then we detail our proposal.

3.1    Parameters

Based on a security parameter λ, different other parameters are generated as listed in [15] to build the new scheme:

1. γ: the bit length of the real and imaginary parts in the public key (γ = ω(η²log₂λ)).
2. ρ: the bit-length of the real and imaginary parts in the noise (ρ = ω(log₂(λ)).
3. η: the bit length of the secret key (.
4. ρ⁰: extra noise parameter.
5. τ: The number of public keys (τ ≥ γ + ω(log₂λ)).

3.2    Somewhat Homomorphic Complex Scheme Construction

The SH complex scheme construction is based on the following steps:

1. Secret key: The secret key s_k is defined by an η bit prime integer p.
2. Public keys: We build a public key bank (PK) formed of τ complex numbers having the following form:

For each complex public key (p_k1^h +ip_k2^h), we build different parameters as follow: ^2η random integer: q^h_j ←− Z ∩ [0, ), random noise pap

rameter: _j^h ←− Z ∩ (−2^ρ,2^ρ) where j ∈ {1,2}. (p_k1^h, p_k2^h) should have different parities. (₁^h, ₂^h) should have the same parity. Encryption Function: The encryption of any bit m is given by the following equation:

4. Decryption Function:

Following 4, we can demonstrate that c = Enc(p_k,m) =

Where modNear(x, p) = y, such that y. Decryption works as long as:  and (r₁^h − r₂^h) are even integers.

The decryption condition is satisfied as long as: |R₁^h| <<< h^p− 2h|, |R2^h| <<< 6|1h^p+ 2h|, |r₁^h−r₂^h| << 6^p and each 6|1 pair of (₁^h,₂^h), (r₁^h,r₂^h) is formed of two integers having the same parity.

3.3    Complex Homomorphic Properties

We show in this section that the proposed scheme satisfies the homomorphic properties. Given two cipher-texts c₁, c₂ respectively for 2 different plain-texts m₁, m₂ encrypted using the complex scheme listed in section 3.2.

c1 = (pk1h + ipk2h)(R1h + iR2h) + r1h + ir2h + m1 = (pq1hR1h − pq2hR2h + R1h1h − R2h2h + r1h + m1) + i(pq1hR2h + pq2hR1h + R2h1h+R1h2h+r2h). c2 = (pk1t +ipk2t)(R1t +iR2t)+r1t +ir2t +m2 = (pq1tR1t − pq2tR2t +R1t1t −R2t2t +r1t +m2)+i(pq1tR2t + pq2tR1t + R2t1t + R1t2t + r2t).

1. Addition

Decryption of c₁ + c₂ is obtained by calculating mod(modNear(real(c₁ + c₂) − imag(c₁ + c₂), p),2) having the following form:

pQadd + Radd + m1 + m2 such that Radd = R1h(1h − 2h) − R2h(1h + 2h) + R1t(1t − 2t) − R2t(1t + 2t) + (r1h − r2h) +

(r1t − r2t).

−p Decryption works as long as R_add is even and R_add ≤

2. Multiplication

Similar to addition, decryption of c₁ × c₂ is obtained by calculating mod(modNear(real(c₁ × c₂) − imag(c₁ × c₂), p),2). We can demonstrate that real(c₁ × c₂) − imag(c₁ × c₂) have the following form:

pQmult + Rmult + m1m2 such that Rmult = (r1tR1h + m2R1h − r2tR2h)(1h−2h)−(r1tR2h+r2tR1h+m2R2h)(1h+2h)+(r1hR1t+

m1R1t − r2hR2t)(1t − 2t) − (R1tr2h + r1hR2t + m1R2t)(1t +

2t) + (R1hR1t1h − R2hR2t1h)(1t − 2t) + (R2hR2t2h −

R1hR1t2h)(1t + 2t) − (R1hR2t1h + R2hR1t1h)(1t + 2t) − (R2hR1t2h + R1hR2t2h)(1t − 2t) + r1h(r1t − r2t) − r2h(r1t +

r2t) + m2(r1h − r2h) + m1(r1t − r2t). −p

              Decryption also works as long as R_mult is even and  R_mult. We can simply demonstrate that R_add and R_mult are even since each couple of (r₁^h,r₂^h), (r₁^t,r₂^t), (₁^h,₂^h) and (₁^t,₂^t) is formed of two integers having the same parity, satisfied.

As a conclusion our new complex scheme is SH that supports a bounded number of addition and multiplication operations over the cipher-texts.

3.4     Making the Complex Scheme Fully Homomorphic

To make our complex scheme FH, we apply Bootstrapping [15, 17] in order to reduce the noise level after each operation. Starting from a complex cipher c, the plain-text m can be calculated following c∗

∗              _∗ this equation m ← [c − b  e]₂ where c = real(c) − imag(c) since p

this decryption equation is much simpler than Equation. 5. First of all we can use Gentry’s transformation to squash the decryption circuit. In this transformation we add to the public key some extra information about the secret key, and use this extra information to post process the cipher-text c^∗. The post processed cipher-text c^∗ can be decrypted more efficiently than the original cipher-text.

3.4.1    Bootstrapping:

Consider the evaluation procedure given in 1, we use instead of the arithmetic circuit L, the decryption circuit D_α of the SH scheme α. The main concept of Bootstrapping is that we have a cipher-text ψ₁ that encrypts m under p_k1 that we want to refresh. s_k1 is the secret key related to the public key p_k1. s_k1 is encrypted under another public key p_k2. Let s_k1j be the encrypted secret bits j of s_k1 under p_k2. Bootstrapping is given by this algorithm:

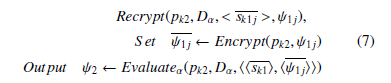In 7, the function Evaluate_α takes as input the bits of s_k1 and ψ₁, each encrypted under p_k2 to evaluate homomorphically the decryption circuit D_α. The output ψ₂ is an encryption under p_k2 of Decrypt(s_k1,ψ₁) = m. By applying 7, we are removing the error vector associated to the first cipher and adding another error vector. The progress is made as long as the second error vector in ψ₂ is shorter than the primitive in ψ₁.

In Figure. 2, we present the evaluation procedure of a circuit with high depth giving birth to a cipher c with a high noise level.

As given in Figure. 3, for a cipher c consider D_c(sk) = Decrypt_sk(c), this operation is called squashing the decryption circuit (will be explained in the upcoming section) and D_c(.) is a low depth polynomial in sk. Bootstrapping consists of evaluating D_c(.) using the encryption of the secret key sk.

3.4.2     Squashing the Decryption Circuit:

Bootstrapping is possible as long as the decryption circuit is an arithmetical circuit of low depth. Squashing is the required transformation in making it possible as listed in[15, 16, 17, 18, 19].

Following Gentry’s Squashing technique, we add three different extra parameters κ, θ, Θ that are function of the security parameter γη       ^∗

λ. κ = ρ₀ , θ = λ, Θ = ω(κ.log(λ)). For a secret key s_k = p and a public key p^∗_k from the original complex homomorphic scheme α, we add to the public key a set Y = {y₁,y₂,y₃,…,y_Θ} of rational numbers in [0,2) with κ bits of precision, such that there is a sparse

X 1 subset S ⊂ {1,2,3,…,Θ} of size θ with    y_i ≈          (mod2). p i∈S

The secret key becomes the indicator of the subset S. The scheme of section 3.2 becomes FH complex by first applying the following modifications:

1. KeyGen:

Generate s^∗_k = p and p^∗_k as before. set x_p ← b p e. Choose randomly a Θ bit vector →−s with hamming weight θ, ^→−s = hs₁, s₂,…, s_Θi and let S = {i; s_i = 1 in vector S }. Choose Θ random integers u_i ∈ Z ∩ [0,2^κ+1), i = 1,2,3,…,Θ sub-and Y = {y₁,y₂,…..,y_Θ}. Hence each y_i is a positive number smaller than 2 with κ bits of precision after the binary point

such that [Xy_i]₂ = (1) − ∆_p for some ∆_p < 2−κ. p i∈S

2. Encrypt and Evaluate Algorithm:

Generate the cipher-text c = real(c) − imag(c) from a complex cipher c. Then for each i ∈ {1,2,3,…,Θ}, set z_i ← [c^∗.y_i]₂ keeping only n = dlogθe + 3 bits of precision after the binary point for each z_i. Output both c^∗ and

3. Decrypt and Output Algorithm:

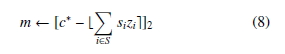Lemma 1. For every cipher-text (c^∗,^→−z ) that is generated by evaluating a circuit C, it holds that ^P_i s_iz_i is within  of an integer.

Proof. Fix an arithmetic circuit L, public keys and secret keys generated with respect to the security parameter λ, with {y_i}^Θ_i=1 the rational numbers in the public key and {s_i}^Θ_i=1 the secret key bits. If we recall that y_i’s were chosen

i cipher-texts {c_i}^t_i=1 that encrypts the input to L and denote: c = Evaluate(pk, L,c₁,c₂,..,…,c_t), we need to establish this equation:

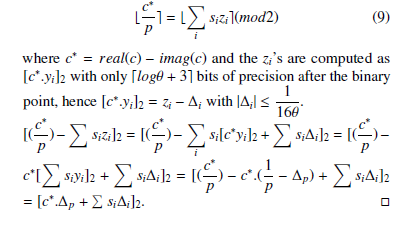We claim that the final quantity inside the brackets has magnitude at most . By definition, since c^∗ is a valid cipher-text

                                      c∗                              1

output, the value   is within      of an integer. Together all p          8

these facts imply the lemma. To establish the claim, we firs observe that | s_i∆_i| ≤ θ ×. Regarding c^∗∆_p, recall that the output c^∗ is obtained by evaluating the circuit L on the cipher-text c_i as listed in [15], for any polynomial P that implements the circuit L, for any α ≥ 1, if P’s input has magnitude at most 2α(ρ +2), its output magnitude at most 2α(η−4). In particular, when P’s are fresh cipher-texts, which have magnitude at most 2^γ, P’s output cipher-text c^∗ has magnitude at most 2γ(η−4)(ρ +2) < 2κ−4. Thus |.

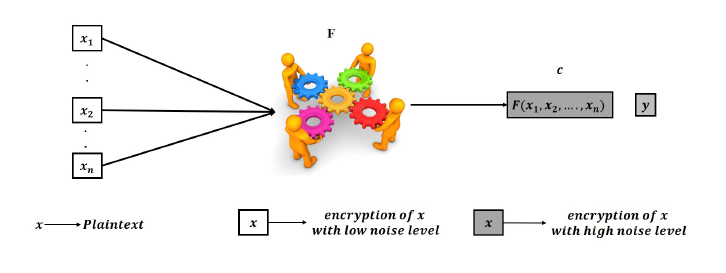Figure 2: Circuit Evaluation with High Noise

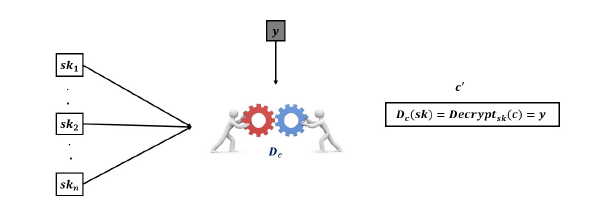Figure 3: Fresh Cipher Generation

3.4.3     Practical Implementation of Squashing and Bootstrapping:

For the squashed decryption circuit given in 8, the implementation of

^Pi_∈S s_iz_i ( such that z_i = (z_i1,z_i2,….,z_in) is a vector of n = dlogθe +3 bits, where 1 ≤ i ≤ Θ), can be done with lower computational complexity as implemented in [16, 19]. This new implementation is based on dividing the new secret key s in θ boxes of B =         bits θ

each, where each box has a single bit having the value 1. This will lead us to obtain a grade school addition algorithm that requires O(θ²) multiplications instead of O(Θ.θ). The secret key ^→−s is divided into s_k,i, the i^th secret key bit in box k, where 1 ≤ k ≤ θ and 1 ≤ i ≤ B. The resultant equation is:

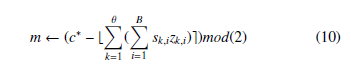We denote that the sum q_k = ^P_i^B₌₁ s_k,iz_k,i is obtained by adding B numbers, only one being nonzero. The decryption equation is now:

Where the q_k’s are rational in [0,2) with n bits of precision after the binary point. Another form of the decryption equation is given by:

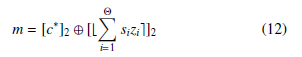Based on 12, we can deduce that the parity of the plain-text m is related to the parity of the primitive cipher-text c^∗ and the parity of [bPΘi=1 sizie]2.

In order to make this concept much clearer, a simple implementation of bootstrapping, using low values, is explained in the following example. Giving randomly Θ = 4, θ = 2, B =  = 2, and

→− a precision bit n = 1. The secret key s = [b₁,b₂,b₃,b₄] such that (b₁ = 1 and b₂ = 0) or (b₁ = 0 and b₂ = 1), (b₃ = 1 and b₄ = 0) or (b₃ = 0 and b₄ = 1) based on the implementation of

10. Initial values for evaluating the decryption circuit using the

→−

secret key s without encryption are s₁ = [s₁₁ s₁₂] = [b₁ b₂], s₂ = [s₂₁ s₂₂] = [b₃ b₄], the z values are taken just as an example z₁ = [z₁₁ z₁₂] = [[10] [01]], z₂ = [z₂₁ z₂₂] = [[11] [01]]. We start by applying the evaluation procedure over the plaintexts by calculating Sum = ^Pθk=₁ ^P_i^B₌₁ s_k,iz_k,i = ^P2_k=₁ ^P2_i=₁ s_k,iz_k,i =

(b1z11 + b2z12) + (b3z21 + b4z22) = [b1                        b2] + [b3                b3 + b4] =

4. Implementation and Security Analysis

In order to validate our work, first we did an implementation of our new Complex-based scheme, then we compared the evaluation of the logic circuit C = (b₀ ⊕ b₁) • (b₂ ⊕ b₃) using the two schemes: Complex and BGV.

As a brief overview of the BGV [20, 21], it is a FHE scheme that works over bit level and built using Lattice based cryptography. The security of this scheme depends on the hardness of Learning With Error (LWE) introduced by Oded Regev in [25], that relies on the complexity of solving a noisy linear system. Starting from a security parameter λ, we have a secret key s ∈ Z^[1_p ^,n] and a cipher-text c ∈ Z^[_p^n,1]. The hardness of LWE resides in taking the lattice dimension: n ≈ poly(λ) and the ring dimension: p ≈ poly(n) following [21, 25]. Homomorphic addition is achieved by simply adding the

Figure 4: Circuit Evaluation over Cipher-texts.

two cipher-texts, while homomorphic multiplication is done by calse_s(1)z₂₂. An implementation of circuit evaluation over the cipherculating the Tensor product of the two different cipher-texts which texts is given in Figure.4. increases the dimension exponentially. Key Switching (KS) is a

As shown in Figure.4, after applying the binary summation over new technique introduced to reduce the cipher dimension after each ^{such that3}11⁾rr⁺1133 −+ⁱ⁽rr^r1211²¹rr^Sum+2233))^r++²³bb^)enc11⁺⁽⁰⁾2133^b++¹ bb⁼⁺33^bp2111³⁽+^Q+^. 1bb^0R1123rr⁺+21313++^iQ1321bb−⁰331^I3rr⁾2)12111⁺+++23⁽)(((+r¹¹221322(++r⁺1113+21331¹1³++r+⁾11⁺r21114423ⁱ))⁽+1+3+−²¹r((rr21r⁺2122231++32²1³+rr⁾−2133⁺rr++1321⁽rr^r21214243¹¹))).))⁺+++             homomorphic multiplication. The basic BGV scheme is SH sincethe noise level will increase with circuit depth, therefore MS isarithmetic operation and extend to a higher circuit depth.another technique introduced to reduce the noise level after eachGACD attack. All simulations are done under Python with SAGE-Math Library using a machine having the following specificationsFinally a crypt-analysis of the new scheme is validated with the

(CPU: Intel Xeon, E5 − 2630, 2.40 GHZ, 8 CORES, 128 GB RAM). b₁+b₃ and mod(modNear(real(Sum_enc(1))−imag(Sum_enc(1)), p),2) = b₁b₃ + b₂ + b₃ + b₄, as long as the encryption parameters are chosen such that the scheme is SH (i.e Sum_1enc and Sum_2enc are formed of             4.1 complex ciphers that can be added and multiplied homomorphically as long as the scheme is SH). Based on all the calculations listed         1. above, a fresh cipher-text of c^∗ can be written as:

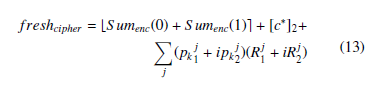Implementations and Results

First Implementation : First implementation with the new Complex-based scheme is done with three different security layers (small: λ = 42, ρ = 26, η = 988, γ = 147456, Θ = 150, τ = 158), (medium: λ = 52, ρ = 41, η = 1558, γ = 843033, Θ = 555, τ = 572), (large: λ = 62, ρ = 56, η = 2128, γ = 4251886, Θ = 2070, τ = 2110) with extra noise parameter ρ⁰ = η − ρ, θ the hamming weight of vector (pk1 + ipk2)(R1 + iR2) →− j s is equal to 15, n the precision after the binary point of each

Table 1: First Implementation Results

Parameters	KeyBankGen	Encrypt	Decrypt
small	0.136439000002 s	0.00102999999945 s	0.000683999998728 s
medium	2.732191 s	0.00130100000024 s	0.00339099999837 s
large	48.049091 s	0.00596199999927 s	0.0216390000023 s

Table 2: Second Implementation Results

Parameters	Complex mean execution time	BGV mean execution time
small	0.4102108 s	0.35041905 s
medium	2.8407822 s	2.42358273 s
large	27.40187732 s	38.52468052 s

z_i is taken as 4. Table. 1 shows in terms of execution time the generation of public key bank of τ complex public keys, 1 bit encryption and decryption.

2. Second Implementation : In the second implementation, we did the evaluation procedure of the logic circuit C =

                 Plainoutput = (b0 ⊕ b1) • (b2 ⊕ b3), (i.e.              CipherOutput =

((c₀ + c₁) × (c₂ + c₃), where c_i = Enc(b_i), for 0 ≤ i ≤ 3) using the two schemes (Complex and BGV) with the same level of security λ. For BGV the three layers of implemenn20

           tation are (small:   )),

⁶), q ≈ O n6 )), (large: (medium: λ = 52, n = 149, p ≈ O(n

n6

)). Table.2 shows

a comparison in terms of mean execution time between the two implementations for 100 iterations (Evaluation procedure for the Compplex-based scheme is done with Bootstrapping mechanism while with BGV is achieved with KS and MS). In addition, results have shown that noise is efficiently reduced for the two schemes. One can see that for large case, the proposed Complex based-scheme performs better that BGV.

4.2.  Security Analysis:

The crypt-analysis of the homomorphic encryption schemes will consider the techniques used to build such schemes. The security of the BGV-lattice based scheme relies on the hardness of solving LWE problems [25]. As for our new complex scheme, it uses mathematical operations and the typical attack in this case is General Approximate Common Divisor (GACD). Given a public key bank PK = {x₁, x₂,…., x_τ} where x_j = pq_j + r_j for 1 ≤ j ≤ τ, the basic idea of this attack is to reveal the value of the secret key p starting from PK. The secret key p can be revealed using different types of algorithms like the approximate GCD of two numbers discussed in [22], the approximate GCD of many numbers using the SDA algorithm [23] by applying a lattice based attack with LLL algorithm. Recently a new improved attack was introduced and implemented in [24], [19]. In our crypt-analysis, we tried to apply this new Approximate GCD attack. Given the public key bank PK = {x_j,1 ≤ j ≤ τ}, where q_j ∈ [0, 2^γ ) and r_j ∈ [0,2^ρ) are p chosen uniformly and independently at random. The algorithm is as follows: For j = 1,2,….,τ, let:

Equation 14 shows clearly that p divides the GCD g = gcd(y₁,y₂,….,y_τ). To build this attack and depending on the choice of the (q_j,r_j), we will try to find a certain bound B not much larger than 2^ρ that with a high probability, all the prime factors of g except p are smaller than this bound B. The probability that all the prime factors of g except p are smaller than B is done based on [19]: ”For every prime p ≥ B other than p, not all the x_j’s are congruent to one of (0,1,…,2^ρ − 1) modp”. This happens with probability very 2ρ _s close to 1 − (  ) . Hence, the probability that all the prime factors p of g except p are smaller than B is essentially given by the following Euler product: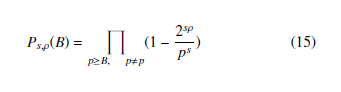

Based on [19] and using the usual prime counting function π(x) explained in [26], we can demonstrate that 15 converges to some positive number smaller than 1 and satisfies the following lemma:

Lemma 2. For any B > 2^ρ+1s , we have:

                            2s              2sρ

1 − P^s,ρ(B) < s − 1 × B^s−1logB

s + 1

ρ In our simulation, we picked B = 2s − 1 and we got a success probability P_s,ρ(B) > 1 − 2^−ρ. The GACD attack is given by the pseudo code of Algorithm 1.

Fa ← Factorial(B) x ← p × random integer(0,2^γ−η) + random integer(0,2^ρ)

i ← 0

g ← 1

while i < 2^ρ do g ← g × (x − i) i ← i + 1 end while j ← 1

while j ≤ s do

x ← p×random integer(0,2^γ−η)+random integer(0,2^ρ)

• ← 0

z ← 1

while i < 2^ρ do z ← z × (x − i) i ← i + 1 end while

g ← Greatest divisor of gcd(g,z) prime to Fa if blog₂(g)c ≤ η then

Break end if

• ← j + 1

end while

return g end procedure

Due to the limited resources of our machine (CPU: Intel Xeon, E5-2630, 2.40 GHZ, 8 CORES, 128 GB RAM), the proposed GACD attack with the security levels related to λ is not feasible since the polynomial y_j given in 14 is of degree 2^ρ with coefficients of size γ and requires a memory of size 2^ργ bits. The required size of each level is: small : 1.125 Terra Byte, medium : 210759 Terra Byte, large : 34831286272 Terra Byte, while our machine is only 128 GB RAM.

5. Conclusion

In this paper, we profited from the simplicity of complex numbers properties by proposing a new SWE scheme based on complex numbers. We applied Gentry refresh mechanism to make our scheme FH. We then implemented our new scheme with the BGV using SAGEMath library. As a comparison with BGV, a well known FHE scheme, our new scheme is an efficient homomorphic scheme and performs better than BGV in terms of execution for large implementation. In addition, our scheme is simply based on simple complex operations rather than lattice based cryptography (homomorphic complex multiplication is done without dimension expansion rather than Tensor product) and Bootstrapping can support unbounded circuit depth, while MS used with BGV is limited to some circuit depth. Finally a crypt-analysis based on GACD attack is presented. Future work will consider the implementation of the GACD Attack given in section 4.2 with a more powerful machine in order to evaluate the approximate attack time.

Acknowledgment

This work has been partially funded with support from the Lebanese University.

1.  R. Rivest, L. Adleman, and M. Dertouzos, “On data banks and privacy homo- morphisms,” in Foundations on Secure Computation, Academia Press, 1978, pp. 169–179. [Online]. Available: http://www.oalib.com/references/14708317
2.  R. L. Rivest, A. Shamir, and L. Adleman, “A method for obtaining digital signa- tures and public-key cryptosystems,” Commun. ACM, vol. 26, no. 1, pp. 96–99,
   Jan. 1983. [Online]. Available: http://doi.acm.org/10.1145/357980.358017
3.  P. Martins, L. Sousa, and A. Mariano, “A survey on fully ho- momorphic encryption: An engineering perspective,” ACM Comput. Surv., vol. 50, no. 6, pp. 83:1–83:33, Dec. 2017. [Online]. Available: http://doi.acm.org/10.1145/3124441
4.  L. Zhang, Y. Zheng, and R. Kantoa, “A review of homomorphic encryption and its applications,” in Proceedings of the 9th EAI International Conference on Mobile Multimedia Communications, ser. MobiMedia ’16. ICST, Brussels, Belgium, Belgium: ICST (Institute for Computer Sciences, Social-Informatics and Telecommunications Engineering), 2016, pp. 97–106. [Online]. Available: http://dl.acm.org/citation.cfm?id=3021385.3021405
5. C. Aguilar-Melchor, S. Fau, C. Fontaine, G. Gogniat, and R. Sirdey, “Recent advances in homomorphic encryption: A possible future for signal processing in the encrypted domain,” IEEE Signal Processing Magazine, vol. 30, no. 2, pp. 108–117, March 2013. [Online]. Available: http://doi.acm.org/10.1109/MSP.2012.2230219
6. S. Fau, R. Sirdey, C. Fontaine, C. Aguilar Melchor, and G. Gogniat, “Towards practical program execution over fully homomorphic encryption schemes,” in 2013 Eighth International Conference on P2P, Parallel, Grid, Cloud and Internet Computing (3PGCIC-2013), Compie`gne, France, Oct. 2013, pp. –. [Online]. Available: https://hal.archives-ouvertes.fr/hal-00917061
7.  P. Paillier, “Public-key cryptosystems based on composite degree residuosity classes,” in Advances in Cryptology — EUROCRYPT ’99, J. Stern, Ed. Berlin, Heidelberg: Springer Berlin Heidelberg, 1999, pp. 223–238. [Online].
   Available: https://link.springer.com/chapter/10.1007/3-540-48910-X 16
8.  M. Nassar, A. Erradi, and Q. M. Malluhi, “Paillier’s encryption: Implementa- tion and cloud applications,” in 2015 International Conference on Applied Research in Computer Science and Engineering (ICAR), Oct 2015, pp. 1–5. [Online]. Available: https://ieeexplore.ieee.org/document/7338149
9.  J. D. i Ferrer, “A new privacy homomorphism and applications,” Information Processing Letters, vol. 60, no. 5, pp. 277 – 282, 1996. [Online]. Available: http://www.sciencedirect.com/science/article/pii/S0020019096001706
10.  J. Domingo-Ferrer, “A provably secure additive and multiplicative privacy homomorphism*,” in Information Security, A. H. Chan and V. Gligor, Eds. Berlin, Heidelberg: Springer Berlin Heidelberg, 2002, pp. 471–483. [Online].
    Available: https://dl.acm.org/citation.cfm?id=744660
11. K. Hariss, H. Noura, and A. E. Samhat, “Fully enhanced ho- momorphic encryption algorithm of more approach for real world applications,” Journal of Information Security and Applications, vol. 34, no. Part 2, pp. 233 – 242, 2017. [Online]. Available: http://www.sciencedirect.com/science/article/pii/S2214212616303052
12. K. Hariss, H. Noura, A. E. Samhat, and M. Chamoun, “Design and realization of a fully homomorphic encryption algorithm for cloud ap- plications,” in Risks and Security of Internet and Systems, N. Cuppens,
    F. Cuppens, J.-L. Lanet, A. Legay, and J. Garcia-Alfaro, Eds. Cham: Springer International Publishing, 2018, pp. 127–139. [Online]. Available: https://link.springer.com/chapter/10.1007/978-3-319-76687-4 9
13.  C. Gentry, “A fully homomorphic encryption scheme,” Ph.D. disser- tation, Stanford, CA, USA, 2009, aAI3382729. [Online]. Available: https://dl.acm.org/citation.cfm?id=1834954
14.  G. Craig, “Fully homomorphic encryption using ideal lattices,” in Proceedings of the Forty-first Annual ACM Symposium on Theory of Computing, ser. STOC ’09. New York, NY, USA: ACM, 2009, pp. 169–178. [Online]. Available: http://doi.acm.org/10.1145 6440
15.  M. van Dijk, C. Gentry, S. Halevi, and V. Vaikuntanathan, “Fully homomorphic encryption over the integers,” in Advances in Cryp- tology – EUROCRYPT 2010, H. Gilbert, Ed. Berlin, Heidelberg: Springer Berlin Heidelberg, 2010, pp. 24–43. [Online]. Available: https://link.springer.com/chapter/10.1007/978-3-642-13190-5 2
16.  C. Gentry and S. Halevi, “Implementing gentry’s fully-homomorphic encryption scheme,” in Advances in Cryptology – EUROCRYPT 2011, K. G. Paterson, Ed. Berlin, Heidelberg: Springer Berlin Heidelberg, 2011, pp. 129–148. [Online]. Available: https:
    //link.springer.com/chapter/10.1007/978-3-642-20465-4 9
17.  C. Gentry, S. Halevi, and N. P. Smart, “Better bootstrapping in fully homomorphic encryption,” in Public Key Cryptography – PKC 2012,
    M. Fischlin, J. Buchmann, and M. Manulis, Eds. Berlin, Heidel- berg: Springer Berlin Heidelberg, 2012, pp. 1–16. [Online]. Available: https://link.springer.com/chapter/10.1007/978-3-642-30057-8 1
18. J.-S. Coron, A. Mandal, D. Naccache, and M. Tibouchi, “Fully homomorphic encryption over the integers with shorter public keys,” in Advances in Cryptology – CRYPTO 2011, P. Rogaway, Ed. Berlin, Heidelberg: Springer Berlin Heidelberg, 2011, pp. 487–504. [Online]. Available: https://link.springer.com/chapter/10.1007/978-3-642-22792-9 28
19. J.-S. Coron, D. Naccache, and M. Tibouchi, “Public key compression and modu- lus switching for fully homomorphic encryption over the integers,” in Advances in Cryptology – EUROCRYPT 2012, D. Pointcheval and T. Johansson, Eds. Berlin, Heidelberg: Springer Berlin Heidelberg, 2012, pp. 446–464. [Online].
    Available: https://link.springer.com/chapter/10.1007/978-3-642-29011-4 27
20. Z. Brakerski and V. Vaikuntanathan, “Fully homomorphic encryption from ring-lwe and security for key dependent messages,” in Proceedings of the 31st Annual Conference on Advances in Cryptology, ser. CRYPTO’11.
    Berlin, Heidelberg: Springer-Verlag, 2011, pp. 505–524. [Online]. Available: http://dl.acm.org/citation.cfm?id=2033036.2033075
21. Z. Brakerski, C. Gentry, and V. Vaikuntanathan, “(leveled) fully homo- morphic encryption without bootstrapping,” in Proceedings of the 3rd Innovations in Theoretical Computer Science Conference, ser. ITCS ’12. New York, NY, USA: ACM, 2012, pp. 309–325. [Online]. Available: http://doi.acm.org/10.1145/2090236.2090262
22. N. Howgrave-Graham, “Approximate integer common divisors,” in Cryptography and Lattices, J. H. Silverman, Ed. Berlin, Heidel- berg: Springer Berlin Heidelberg, 2001, pp. 51–66. [Online]. Available: https://link.springer.com/chapter/10.1007/3-540-44670-2 6
23. J. C. Lagarias, “The computational complexity of simultaneous diophantine approximation problems,” SIAM J. Comput., vol. 14, no. 1, pp. 196–209, Feb. 1985. [Online]. Available: http://dx.doi.org/10.1137/0214016
24.  Y. Chen and P. Q. Nguyen, “Faster Algorithms for Approximate Common Divisors: Breaking Fully-Homomorphic-Encryption Challenges over the Integers,” in EUROCRYPT 2012, ser. Lecture Notes in Computer Science,
    D. Pointcheval and T. Johansson, Eds., vol. 7237, IACR. Cambridge, United Kingdom: Springer, Apr. 2012, pp. 502–519. [Online]. Available: https://hal.inria.fr/hal-00864374
25.  O. Regev, “On lattices, learning with errors, random linear codes, and cryptography,” in Proceedings of the Thirty-seventh Annual ACM Symposium on Theory of Computing, ser. STOC ’05. New York, NY, USA: ACM, 2005, pp. 84–93. [Online]. Available: http://doi.acm.org/10.1145/1060590.1060603
26. E. Bach and J. Shallit, Algorithmic Number Theory. Cam- bridge, MA, USA: MIT Press, 1996. [Online]. Available: https:
    //link.springer.com/chapter/10.1007 53-9 2

(Click Here)

(Click Here)