1. Introduction

The Fourth Industrial Revolution has increased the demand for engineers [1] [2] [3]. Until recently, computer science was learned by university students, often in engineering fields. Because of a shortage of engineers in many countries, attempts have been undertaken to introduce computer science into secondary school education.

A study suggested that the high school ICT curriculum should focus on computer science [4]. A report by the Royal Society of the United Kingdom emphasized the importance of computer science skills in primary education [5]. The report pointed out problems in ICT education, such as those in class content and the loss of opportunities for students. In addition, it proposed to redefine ICT into three areas, namely computer science, information technology, and digital literacy, among which computer science is a particularly important area. The movement to implement programming education is accelerating globally.

For introducing programming in school education, many problems have been identified and various teaching methods have been proposed [6] [7]. A report summarizing three years of compulsory programming education in the UK published in 2014 found that it was patchy and fragile [8]. The report briefly discussed the difficulty of programming education.

A student’s inherent interest in computer programming affects learning. Learners with an interest in programming can effectively learn in large groups with a single teacher, as is done in the university. Such learners can solve problems by investigating them or asking questions. However, traditional teaching methods may be unsuitable for novices and learners who are not interested in programming. One of the most effective ways for novices to learn is one-on-one learning with a teacher. This is especially true for programming because programs that accomplish a given task can be written in various ways. Teachers must thus strictly evaluate the program written by a learner.

Programming includes complex language constructs and requires logical thinking, similar to that used in mathematics. Programmers must consider algorithms, memory space, execution time, and code size. However, exhaustive and quantitative evaluation of programs by a human teacher is difficult. In addition, programs may not work as expecting due to various bugs. It is difficult even for experienced teachers to deal with every bug.

To improve this situation, it is necessary to assign a knowledgeable teacher to several novice programmers. However, this is not possible in classes that introduce programming due to a lack of human resources. To solve this problem, methods for estimating the difficulty of programming problems using cluster analysis and problem recommendation algorithms have been proposed [9] [10]. In addition, attempts have been made to identify early crisis situations experienced by novice programmers using clustering [11]. However, many studies considered only optimizing human resources and presenting a course to users. The quality of teaching still depends on the actual teacher. To solve this problem comprehensively, an intellectual tutoring system is required.

Online judge systems are environments in which programming can be learned independently [12]. An online judge is an online execution environment that executes and verifies source code submitted by users. Users can improve their programming skills by solving problems in various categories (e.g., syntax, semantics, algorithms, data structures). In addition to automatic verification, an online judge provides a quantitative performance evaluation (execution time, memory usage, etc.) of the program. Although online judges satisfy certain requirements of an autonomous learning environment, it is extremely difficult for novice programmers to continue learning using online judges because they do not provide concrete feedback. Originally, online judges were created for programming contests, in which a solution is either accepted or rejected. Thus, programmers can only recognize that their program has an error, not which type of error (e.g., logic error, compile error, run-time error). For such a program, which is “executable for any input”, but “does not satisfy the specifications of the problem”, the judgment does not provide useful support for the user. Therefore, novice programmers tend to give up if their logic errors cannot be debugged.

There are various approaches to programming education, including methods that use program execution traces and program dependence graphs. Here, we propose a logic error detection algorithm based on structure patterns, error degree, and abstract syntax trees. A structure pattern is a list generated from the corresponding abstract syntax tree and is an index of similarity at the structure level. An error degree is a value generated from a result of the detection algorithm and is an index of similarity at the characteristic level. The goal of the proposed algorithm is to provide optimal and personalized feedback to individuals. The proposed algorithm provides personalized feedback based on filtering using structure patterns, error degree, and the characteristics of abstract syntax trees.

In this paper, an algorithm for detecting logic errors and the corresponding API, which can be used to construct intelligent coding editors, are presented. The results of quantitative and qualitative experiments are shown. The quantitative experiments are used to verify the detection range of logic errors. The results show that the proposed algorithm can detect logic errors in many cases. The qualitative experiments are used to determine the detection accuracy and evaluate the appropriateness of feedback based on the detection results. The proposed algorithm is shown to detect logic errors and provide appropriate feedback in many cases. In some cases, generated feedback was inappropriate for learning support. This paper is an extension of the work originally presented in “2018 9th International Conference on Awareness Science and Technology (iCAST)” titled “Logic Error Detection Algorithm for Novice Programmers based on Structure Pattern and Error Degree” [13].

The remainder of this paper is organized as follows. Section 2 presents related research. Section 3 describes the logic error detection algorithm. Section 4 describes the LED API. Section 5 presents experiments that use data from an online judge system. Section 6 shows and discusses the experimental results and suggests possible improvements. Finally, Section 7 summarizes the main conclusions.

2. Related Research

The goal of the present study is to construct an autonomous learning environment for novice programmers. However, autonomous learning of programming has not been clearly defined.

Learner autonomy has been mainly considered in the field of foreign language education by researchers such as Holec [14] [15]. Dickinson proposed the concept of autonomous learning, where learners do not rely on teachers, but are themselves responsible for the results, and make all decisions related to learning [16]. Therefore, autonomous learning can be broadly defined as self-learning controlled by the learner.

This definition of autonomous learning assumes that the learning environment is appropriate. However, there is a shortage of teachers in programming education. In the present study, autonomous learning of programming is defined as autonomous learning in an environment without an actual teacher.

Thus far, a number of approaches to support novice programmers have been proposed. In this paper, we present methods that have different targets and structures, and require different educational resources.

Wu et al. designed practice teaching and assessment methods around an online judge system and proposed resolution methods for existing problems in hybrid learning [17]. Semi-automatic evaluation methods that focus on reducing the burden on teachers have also been proposed [18]. In this approach, students are grouped according to the structure of their source code submitted to the online judge, and guidance is provided for each group. Using a network of online judge users, a hybrid method that allows other users to be asked for guidance has been proposed [19]. This approach uses a clustering result based on the similarity of source code. In addition, a method that uses solutions and a language model based on long short-term memory (LSTM) networks for bug detection has been proposed [20].

Fault localization with program execution traces is a well-known technique for detecting logic errors. Using this concept, Su et al. constructed a Moodle-based online learning environment to provide feedback for logic errors [21]. In a study related to this technique, the accuracy of logic error detection using only 20% of the source code and the effectiveness of feedback using a lightweight spectrumbased algorithm were verified [22].

There are approaches that target specific logic errors to support novices. These approaches focus primarily on conditional branches and detect common logic errors, such as careless mistakes in conditional expressions, priority violations, and infinite loops [23] [24].

Targeted at advanced novice programmers, FrenchPress [25] is an eclipse plugin that focuses on programming style and supports programmers who have not yet assimilated the object-oriented paradigm.

In the present study, logic errors are detected by comparing a source code that may include logic errors with correct source codes stored in an online judge system. A comparison of source code is generally performed to detect code clones (i.e., similar or identical fragments of code) [26] [27] [28]. The following four types of method are commonly used to detect code clones.

Text-based methods directly compare source code as text. This type of comparison includes a lot of unique information, such as variable names. Token-based methods compare tokens obtained by a lexical analysis of source code. Since this type of comparison is not affected by unique information, such as variable names, it has relatively high accuracy. Tree-based methods compare code based on abstract syntax trees obtained by a syntax analyzer. Since parts unrelated to the meaning of the program are omitted from the syntax tree, the structural information of the source code is used for comparison. Semantic-based methods compare code using various information obtained from a parser. A program dependence graph is primarily used. It is possible to detect discontinuous code clones, which are difficult to find using other methods.

The results obtained from text or token comparison are not necessarily consistent with the structure of the source code. Therefore, it is difficult to generate accurate feedback when using text- and token-based methods for detecting logic errors. Since the program dependency graph used in semantic-based approaches has information on data dependency and control dependency, it is possible to perform a comparison based on semantics rather than the description of source code. However, in the isomorphism judgment of graphs, although the semantics of the programs are the same, it is considered difficult to detect logic errors that differ only in internal values. A comparison using abstract syntax trees is based on the structural information of source code and thus can be performed at the syntax level, considering for example if statements or for statements. Therefore, this method is considered to be suitable for detecting logic errors by a feedback algorithm.

3. Logic Error Detection Algorithm

In the present study, two kinds of source code, namely “wrong code” and “correct code”, are used to demonstrate the proposed algorithm. The wrong code is code submitted to an online judge and judged as

“Wrong Answer”. It is the target for detecting logic errors by the proposed algorithm. The correct code is code judged as “Accepted” and stored in the online judge system. It is the comparison target for detecting logic errors by the proposed algorithm.

3.1      Logic Error

A logic error is a bug in a program that triggers erroneous behavior but does not cause abnormal termination. In other words, logic errors induce behavior not intended by the programmer. Programs that contain logic errors are valid programs that can be compiled and executed. To debug a logic error, the user must determine the cause of the error by tracing variable information during execution using a number of test cases. Table 1 shows some common examples of logic error.

3.2       General Approach of Proposed Algorithm

In the present study, we propose a logic error detection algorithm based on a comparison between wrong and correct code. The proposed algorithm uses a comparison method based on an abstract syntax tree, which is a data structure in which the grammatical structure of source code is represented by finite labeled oriented trees. An abstract syntax tree is recursively defined by a minimum unit, called a syntax, generated by a parser. For example, if and for statements are recursively defined by a number of constructs.

Table 1: Common examples of logic error

Type of logic error	Cause
Loop condition	Incorrect number of iterations of for statement
Conditional branch	Incorrect conditional expression in if statement
Output format	Incorrect rounding
Data type	Incorrect data type
Calculation	Incorrect operator in binary expression
Indexing	Wrong index accessed

In the present study, a construct that is recursively defined by other constructs is denoted as a nonterminal construct, and a construct that is not recursively defined by other constructs is denoted as a terminal construct. Examples of nonterminal constructs are if statements and conditional expressions, and examples of terminal constructs are character strings and numeric values. Specifically, the algorithm compares abstract syntax trees of the target source code by applying the following steps recursively.

1. If the information on terminal constructs of the same kind is not different, it is not judged as a logic error.
2. If the information on terminal constructs of the same kind is different, it is judged as a logic error.
3. If the constructs are the same kind of nonterminal construct, they are compared to each other.
4. In other cases, a logic error is judged to have occurred.

The algorithm detects constructs that are logic errors. Algorithm 1 shows the pseudocode of the logic error detection algorithm.

The proposed algorithm can compare compilable source code. However, because of the characteristics of abstract syntax trees, a comparison of source code with different tree shapes generates detection results that are unsuitable for detecting logic errors. In addition, even if the shapes of the trees are the same, a comparison of code with different node meanings will generate incorrect detection results. Therefore, the proposed algorithm has two phases.

In the first phase, an appropriate comparison target is selected.

The proposed algorithm compares only two source codes and detects logic errors. However, the user may attempt to solve a problem using various approaches. For example, a loop can be implemented using a for statement or a while statement. If the detection algorithm is applied to the source code of programs that have quite different structures, incorrect results will be obtained. Figures 1 and 2 show examples of a comparison of source code that uses different algorithms. A suitable comparison target is required to detect logic errors.

Algorithm 1 Logic Error Detection
Require: x    = expression in wrong code, xn = n-th expression of x y    = expression in correct code, yn = n-th expression of y Ensure: E = an array of Logic Error : Array 1: function Detection(x,y) 2:             E ⇐ empty array
3:	if x and y are terminal constructs of the same kind then
4:	if x and y are the same information then
5:	return E	. Step 1
6:	else
7:	return E ⇐ x	. Step 2
8:	end if
9:	else if x and y are nonterminal constructs of the same kind then
10:	if the number of expressions of x and y are the same then
11:	for i = 1 to the number of expressions in x do
12:	Connect E and Detection(xi,yi) together	. Step 3
13:	end for
14:	return E
15:	end if
16:	end if
17:            return E ⇐ x 18: end function		. Step 4

In the second phase, the best detection result is selected. The proposed algorithm generates feedback for the user based on a comparison of the source code. However, the algorithm that the user employs to solve a problem is independent of the source code structure. For example, how conditional branches and libraries are used depends on the user’s characteristics. If the detection algorithm is applied to the source code of programs with different algorithms,

we may provide feedback while ignoring the characteristics of the corresponding user.

Figures 1 and 3 show examples of a comparison of source code

Figure 1: Example of detection with a for statement approach      that uses different loop constructions. Therefore, we need to give

feedback based on correct codes that has the same characteristics as those of the target codes.

Figure 2: Example of detection with a while statement approach

Figure 3: Example of detection with a decrement algorithm

3.3     Structure Pattern

In the present study, structure patterns are used in the first phase.

A structure pattern is a list generated from the corresponding abstract syntax tree and is an index of similarity at the structure level. Moreover, it is core data obtained by a depth-first search of the abstract syntax tree and includes a list of expressions and block statements. The generated list contains expressions such as a variable declaration and assignment, and control structures such as for and if statements. Therefore, a structure pattern can be considered to express the general form of source code.

Figure 4 shows a sample source code. Figure 5 shows an example of an abstract syntax tree parsed from the sample source code. Table 2 shows an example of a structure pattern generated from the sample source code.

Figure 4: Sample source code

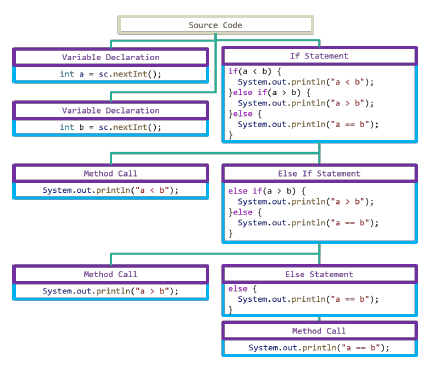Figure 5: Abstract syntax tree for the source code in Figure 4

Programs with the same structure patterns have the same order and kind of constructs. Therefore, we can obtain appropriate comparison targets by filtering correct code using the structure pattern. For example, the structure patterns for the source code in Figures 1 and 2 are shown in Tables 3 and 4, respectively. As shown, appropriate correct codes for comparison can be obtained by filtering according to the structure pattern.

Table 2: Structure pattern for the source code in Figure 4

Index No.	Syntax
1	Variable Declaration
2	Variable Declaration
3	If Statement
4	Method Call
5	Else Statement
6	If Statement
7	Method Call
8	Else Statement
9	Method Call

Table 3: Structure pattern of wrong code and correct code shown in

Figure 1

Index No.	Syntax
1	Variable Declaration
2	For Statement
3	Method Call

Table 4: Structure pattern of correct code shown in Figure 2

Index No.	Syntax
1	Variable Declaration
2	Variable Declaration
3	While Statement
4	Method Call
5	Binary Expression

3.4     Error Degree

In the present study, the error degree is used in the second phase. An error degree is a value generated from a result of the detection algorithm and is an index of similarity at the characteristic level. Moreover, it is a total value obtained by assigning a weight according to the type of detected logic error and can be expressed as

The error degree is zero when the wrong code is compared with itself. An increase in error degree indicates that the source code has characteristics different from those of the wrong code. Therefore, we can obtain optimal feedback by comparing the wrong code with all versions of correct code and by filtering the detection results using the error degree. Table 5 shows the weighting rules. The weight depends on the logic error type in the source code. For example, errors at the element level, such as terminal constructs and operators, have lower weight, whereas errors at the syntax level, such as the type of syntax and its presence in the code, have higher weight. Errors related to the number of constructs are weighted in proportion to this number.

Table 5: Weighting rules for error degree

Error type	Weight
Terminal construct	1
Operators in expressions	3
Number of constructs	2*constructs
Existence of component	5
Construct that exists only on one side	10
Types of construct for comparison	10

The error degree compensates for the weaknesses of filtering by structure pattern. For example, Figures 6 and 7 show the results of logic error detection for the source code of programs with the same structure patterns presented in Figure 1 and Figure 3. As shown in these figures, more accurate feedback can be obtained by calculating the error degree from the detection result.

Figure 6: Detailed detection results for source code in Figure 1

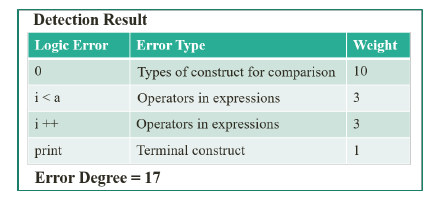Figure 7: Detailed detection result for source code in Figure 3

3.5. Extended Detection Algorithm

The purpose of the proposed algorithm is to support autonomous learning by detecting logic errors in a wrong code and providing the corresponding feedback. The detection algorithm provides feedback through the following steps.

1. Analyze the judged source code and generate a structure pattern.
2. From the data stored in the online judge system, extract correct codes with the same structure pattern.
3. Compare all of the extracted correct codes with the wrong code, and calculate the error degree based on the detection results.
4. Provide information obtained based on the detection result with the lowest error degree as feedback for the user.

Algorithm 2 shows the pseudocode of the extended logic error detection algorithm.

4. Implementation of Algorithm API

Section 3 described the proposed logic error detection algorithm for general online judge systems. In the present study, we also developed an LED web API for the proposed algorithm that is compatible with Aizu Online Judge (AOJ) [29].

4.1. Aizu Online Judge

AOJ is an online judge system developed and operated by the University of Aizu. An online judge system is a service that compiles and executes programs submitted by users and automatically evaluates their accuracy and performance using various test cases and verification machines. At present, AOJ contains source code from 60,000 users and 4 million judgments. AOJ contains various problems, such as those used in programming contests (e.g., ACM-ICPC) and those specific to a certain topic, including Introduction to Programming (ITP), “Algorithm and Data Structures”, and related libraries. For these problems, limit values are set for CPU time and memory usage, and the user can practice by solving the problem under these limitations.

The user obtains a verdict by submitting the answer code for each question to the judge system. The judge system instantly provides feedback (accepted/rejected) based on various test cases for the problem, together with the CPU time and memory usage. The type of failure (Time Limit Exceeded, Memory Limit Exceeded, Runtime Error, etc.) is also given in the feedback. Users can debug their code based on the feedback and resubmit code as many times as desired. In the present study, the aim is to detect logic errors, so we only cover programs corresponding to “Accepted” and “Wrong Answer”.

AOJ has an API for accessing a part of its database. The API can be used for developing various tools. For example, there are submitted source code, submission history including log of trial and error.

4.2. Logic Error Detector API

In the present study, we developed an LED that uses source codes stored in AOJ. Furthermore, by implementing peripheral functions, we developed as a web API for the LED.

Algorithm 2 Extended Logic Error Detection
Require: X    = submitted code Y    = array of accepted programs, Yn = n-th accepted program Ensure: F = Feedback 1: function Extended Detection(X)	. Step 1
2:            R = empty array 3:             pattern ⇐ structure pattern of X	. Step 2
4:            Y ⇐ all the correct codes submitted for a given problem as X 5:            Y ⇐ Y that have the same structure pattern as pattern	. Step 3
6:            for i = 1 to number of Y do 7:                   add detection result based on Algorithm 1(X,Yn) to R	. Step 4
8:            end for 9:            return F ⇐ detection result with the lowest error degree in R 10: end function	. Step 5

From the viewpoint of data availability and practicality, source codes in Java language are analyzed and utilized for the LED API. There are three main reasons for selecting Java. Firstly, it is often adopted as an introduction to object-oriented programming languages for novice programmers. Secondly, it is the second most frequently used language in AOJ. The use of stored data makes it possible to detect logic errors more accurately, so there must be a sufficient number of comparison objects. Thirdly, an open-source library called JavaParser can be used to convert source code written in Java into an abstract syntax tree.

The LED API is implemented using docker containers that serve as a web server, an application server, and a database server. Figure 8 shows an architecture diagram of the LED API.

The web container, based on Nginx, is responsible for front-end processing and acts as a reverse proxy. At the front-end, we implemented tools for research and simple editors using Vue.js and trial of API is possible. The reverse proxy controls access to the application container. Only the web container is exposed to the outside world via the API to prevent attacks on the application and database containers.

The application container is responsible for the back-end processing by the LED, which is the application that implements the proposed algorithm. Since only the host can connect to the database container, it can be used together with the reverse proxy of the web container to prevent attacks on the database container.

LED is a Java application developed using Spring Boot based on Spring Framework. MySQL and Hibernate, as an object-relational mapper, are adopted. JavaParser is used for parsing source code written in Java.

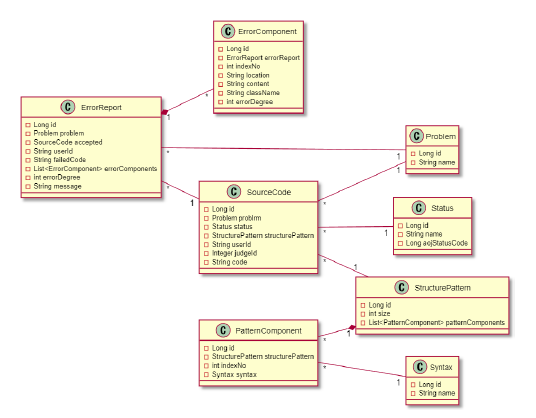
4.3. Class Composition

Figure 9 shows a class diagram of LED. The SourceCode class is used to represent source codes submitted to and stored in AOJ. It has a many-one relation with the Problem, Status, and StructurePattern classes. It includes information on the ID of the user who submitted the code, the ID of the judge, and the submitted code.

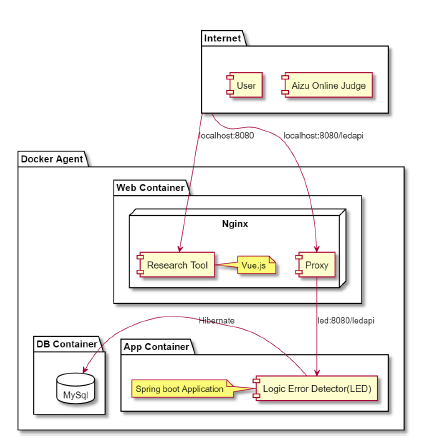Figure 8: LED architecture diagram

The StructurePattern class represents the structure pattern of source code for each program. It has an one-to-many relationship with the SourceCode and PatternComponent classes.

The PatternComponent class is used to represent the type and order of syntax in the structure pattern. It has many-to-one and composition relationships with the StructurePattern class. This is because the structure pattern includes the type and order of syntax, and there are cases where the source code of multiple programs has the same structure patterns, but the pattern component completely depends on the structure pattern.

The ErrorReport class is used to represent the comparison result

Figure 9: LED class diagram

of the logic error detection algorithm and is also a feedback class of the LED API. It has a many-to-one relationship with the SourceCode and Problem classes. It has many-to-one and composition relationships with the ErrorComponent class. It includes information on wrong codes in which logic errors were detected and correct codes used to generate the detection result selected by filtering using the error degree.

The ErrorComponent class is used to represent details of the detected logic error. It has the location, content, class of syntax, and error degree information of the logic error detected in the wrong code.

4.4. Behavior

Figure 10 shows the relationship between classes and objects. The flow of logic error detection using the LED API is as follows.

1. The user submits a source code that is judged as “Wrong Answer”.
2. The wrong code is analyzed and its structure pattern is generated.
3. The structure pattern of the wrong code is searched for in the database.
4. Correct codes with the same structure pattern as that of the wrong code are searched for in the database and used as candidate codes for detection.
5. Using LED, all candidate codes are respectively compared to the wrong code and an error report is generated.
6. The error report with the lowest error degree is provided to the user as feedback.

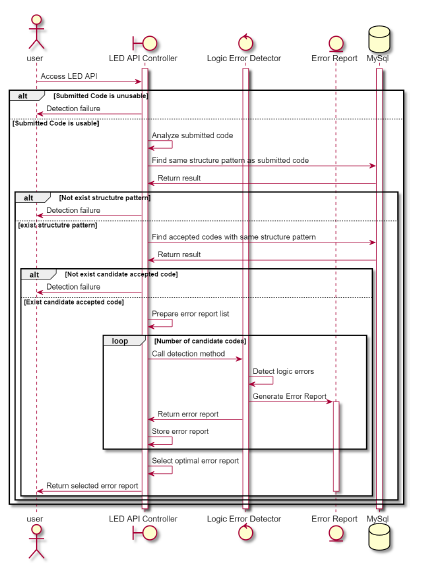Figure 10: LED sequence diagram

5. Experiment

We conducted quantitative and qualitative experiments using the LED API and AOJ. The LED API is first used to detect logic errors in wrong code submitted by a user who has never solved the problem. Therefore, in this experiment, source codes judged to be “Wrong answer” in AOJ were used as wrong codes.

5.1. Basic Dataset from AOJ

AOJ has a problem set for novices called ITP. In this experiment, all problems in ITP were used. The dataset consists of source code that satisfies the following conditions.

• Submitted to solve the target problems.
• Judged as “Accepted” or “Wrong Answer”.
• Written in Java.
• Consists only of the main method.
• Considered not to be created by the same user.

Tables 6 and 7 show the details of the dataset. “Problem Id” is the problem id of the experimental target. “Usable Programs” is the number of available programs. “Structure Pattern” is the number of structure patterns. “Common Pattern Programs” is the number of programs with the most common structure pattern.

5.2. Experiment 1: Quantitative Method

This subsection describes experiments conducted using quantitative methods.

AOJ stores all the source codes submitted by users. Therefore, there are correct and incorrect answers to certain problems submitted by a given user. By comparing correct codes and the wrong code submitted by a given user, it is possible to obtain reliable feedback F necessary for debugging. From the inclusion relation of feedback

F and feedback F’ obtained using the LED API, we measure what portion of logic errors can be detected by the proposed algorithm.

In this experiment, we evaluated whether the following statements are true:

• The LED API can be used to detect all logic errors.
• The LED API can be used to detect some logic errors.

For evaluating the first statement, we measured whether F’ completely includes F. The code debugged based on information provided by feedback F has already been accepted by AOJ. Therefore, when feedback F’ completely includes feedback F, it can be regarded that all the logic errors were detected.

For evaluating the second statement, we measured whether F’ contains some of F. During debugging, a user may modify not only the algorithm, but also variable names, the order of processing, etc. Therefore, when some of feedback F are included in feedback F’, it can be regarded that some logic errors were detected.

The following procedures were applied to each target problem.

1. Apply the proposed algorithm to correct code and wrong code submitted by a given user and obtain feedback F.
2. Generate feedback F’ from the wrong code using the LED API.
3. Determine the inclusion relation of F and F’.

The dataset consists of source code that satisfies the following conditions.

• Correct code and wrong code that submitted by the same user.
• These two programs have the same structure patterns.

5.3. Experiment 2: Qualitative method

This subsection describes experiments conducted using qualitative methods.

In Experiment 1, the accuracy of logic error detection was investigated using a quantitative method. However, the experiment only measured the detection range, and it is not known whether the feedback is sufficient for debugging. Therefore, we manually debugged a code using feedback from the LED API and verified whether the wrong code was acceptable by AOJ. In this experiment, we evaluated whether the following statements are true:

• The LED API can be used to correctly detect logic errors.
• The provided feedback is appropriate for supporting learning.

The following procedures were applied to each target problem.

1. Randomly select a wrong code in AOJ.
2. Detect logic errors using the LED API.
3. Debug the wrong code manually using feedback and verify whether the debugged code is acceptable by AOJ.

Table 6: Problem Information

Problem ID	Topic	Summary of Problem
ITP1_1_A	Getting Started	Print “Hello World” to standard output.
ITP1_1_B		Calculate the cube of a given integer x
ITP1_1_C		Calculate the area and perimeter of a given rectangle.
ITP1_1_D		Read an integer S [second] and convert it to h:m:s.
ITP1_2_A	Branch on Condition	Print small/large/equal relation of given two integers a and b.
ITP1_2_B		Read three integers a, b and c, and print “Yes” if a < b < c, otherwise “No”.
ITP1_2_C		Read integers and print them in ascending order.
ITP1_2_D		Read a rectangle and a circle, and determine whether the circle is arranged inside the rectangle.
ITP1_3_A	Repetitive Processing	Print “Hello World” 1000 times.
ITP1_3_B		Read an integer x and print it as is for multiple test cases.
ITP1_3_C		Read two integers x and y, and print them in ascending order for multiple test cases.
ITP1_3_D		Read three integers a, b, and c, and print the number of divisors of c in [a, b].
ITP1_4_A	Computation	Read two integers a and b, and calculate a / b in different data types.
ITP1_4_B		Calculate the area and circumference of a circle for given radius r.
ITP1_4_C		Read two integers, a and b, and an operator op, and then print the value of a op b.
ITP1_4_D		Read a sequence of n integers ai(i=1,2,…n), and print the minimum value, maximum value, and sum of the sequence.
ITP1_5_A	Structured Program I	Draw a rectangle whose height is H cm and width is W cm.
ITP1_5_B		Draw a frame whose height is H cm and width is W cm.
ITP1_5_C		Draw a chessboard whose height is H cm and width is W cm.
ITP1_5_D		Structured programming without goto statement.
ITP1_6_A	Array	Read a sequence and print it in reverse order.
ITP1_6_B		For given a deck of cards, find missing cards.
ITP1_6_C		Count the number of elements in a three-dimensional array.
ITP1_6_D		Read a n×m matrix A and a m×1 vector b, and print their product Ab.
ITP1_7_A	Structured Program II	Read a list of student scores and evaluate the grade for each student.
ITP1_7_B		Find the number of combinations of integers that satisfy 1) three distinct integers from 1 to n, and 2) sum of the integers is x.
ITP1_7_C		Read the number of rows r, columns c, and a table of r×c elements, and print a new table that includes the total sum for each row and column.
ITP1_7_D		Read a n×m matrix A and a m×l matrix B, and print their product.
ITP1_8_A	Character	Convert uppercase/lowercase letters to lowercase/uppercase.
ITP1_8_B		Read an integer and print the sum of its digits.
ITP1_8_C		Count the number of appearances for each letter (ignoring case).
ITP1_8_D		Find a pattern p in ring-shaped text s.
ITP1_9_A	String	Read a word W and text T, and print the number of times that word W appears in text T.
ITP1_9_B		Read a deck (a string) and shuffle it, and print the final state (a string).
ITP1_9_C		Read a sequence of Taro and Hanako cards and report the final scores of the game.
ITP1_9_D		Perform a sequence of commands including reverse and replace operations.
ITP1_10_A	Math Functions	Calculate the distance between two points P1(x1, y1) and P2(x2, y2).
ITP1_10_B		For the given two sides of a triangle a and b and the angle C between them, calculate the area, circumference, and height of the triangle.
ITP1_10_C		Calculate the standard deviation.
ITP1_10_D		Read two n-dimensional vectors x and y, and calculate Minkowski’s distance, where p=1,2,3, ∞.
ITP1_11_A	Structure and Class	Simulate rolling a dice.
ITP1_11_B		Print the integer on the right side face of the rolled die.
ITP1_11_C		Read two dice and determine whether they are identical.
ITP1_11_D		Read n dice and determine whether they are all different.

6. Results and Discussion

6.1. Results of Experiment 1

Table 8 shows the results of Experiment 1. “Problem Id” is the In this section, we present and discuss the results of each experi- problem id of the experimental target. “All Users” is the number ment. of users who submitted source code. “Usable Users” is the number Table 7: Statistics of the Dataset Used in the Experiment

Problem ID	Number of Programs	Usable Programs	Structure Pattern	Common Pattern Programs
ITP1_1_A	5132	5094	5	5030
ITP1_1_B	4408	3713	50	1274
ITP1_1_C	3292	2743	56	744
ITP1_1_D	2365	1832	68	504
ITP1_2_A	2836	2231	82	629
ITP1_2_B	2283	1683	68	619
ITP1_2_C	2779	1099	71	234
ITP1_2_D	2919	1682	60	628
ITP1_3_A	2290	2194	15	1436
ITP1_3_B	3180	1303	90	71
ITP1_3_C	2538	727	75	67
ITP1_3_D	1622	983	58	261
ITP1_4_A	3715	2605	66	541
ITP1_4_B	2263	1825	56	316
ITP1_4_C	1506	347	49	35
ITP1_4_D	3027	735	48	54
ITP1_5_A	1477	701	65	107
ITP1_5_B	1404	354	46	57
ITP1_5_C	1236	421	53	58
ITP1_5_D	3120	717	58	147
ITP1_6_A	1345	447	46	53
ITP1_6_B	1027	181	25	23
ITP1_6_C	1340	212	19	55
ITP1_6_D	743	295	32	36
ITP1_7_A	1683	196	29	28
ITP1_7_B	1287	230	28	33
ITP1_7_C	839	109	19	14
ITP1_7_D	1207	216	24	37
ITP1_8_A	927	329	44	23
ITP1_8_B	797	227	30	32
ITP1_8_C	1444	152	23	19
ITP1_8_D	721	233	23	44
ITP1_9_A	1409	270	27	35
ITP1_9_B	642	151	17	28
ITP1_9_C	710	174	23	29
ITP1_9_D	613	74	11	17
ITP1_10_A	594	387	28	98
ITP1_10_B	670	339	24	84
ITP1_10_C	935	78	11	17
ITP1_10_D	420	61	8	14
ITP1_11_A	135	20	4	11
ITP1_11_B	109	18	4	9
ITP1_11_C	108	11	2	8
ITP1_11_D	19	0	0	0

of users who submitted both correct and wrong code with the same structure patterns (and thus logic errors can be detected using the LED API). “Whole Success Users” is the number of users for whom all logic errors were detected using the LED API. In other words, this is the result of the first statement. “Partial Success Users” is the number of users for whom some logic errors were detected using the LED API. In other words, this is the result of the second statement. “Whole Success Ratio” is the ratio of Whole Success Users to Usable Users. “Partial Success Ratio” is the ratio of Partial Success Users to Usable Users. “Difference Success Ratio” is the difference between Whole Success Rate and Partial Success Rate.

The first item is the complete detection rate of logic errors. The results of the experiment show that all logic errors were detected for many problems. Overall, we succeeded in detecting logic errors in more than 70% of programs.

The second item is the partial detection rate of logic errors. The results of the experiments show that a higher detection ratio for partial logic errors was achieved for many problems. Overall, we succeeded in detecting logic errors in more than 80% of programs.

6.2. Results of Experiment 2

Table 9 shows the results of Experiment 2. The first item is the detection accuracy of logic errors. Considering the features of the evaluation method, it was considered that logic errors could not be correctly detected when the source code could be modified only by factors outside the feedback range. The results of the experiment show that we successfully detected logic errors in 100% of test cases. Therefore, the proposed detection algorithm has sufficient ability to detect logic errors in wrong code.

The second item is related to the appropriateness of feedback.

The experimental results show that we succeeded in providing appropriate feedback in 80.4% of the test cases. This evaluation item is based on the qualitative method used to verify the appropriateness for supporting learning. Therefore, we should discuss the appropriateness of the judgment.

6.3. Discussion

In this subsection, we discuss the experimental results. Some ideas for improvement based on the experimental results are also given.

6.3.1      Discussion for Experiment 1

The results of Experiment 1 confirm that the proposed detection algorithm can support users who attempt to solve problems. We also confirmed that the detection algorithm can detect all the logic errors in a wrong code in many cases. However, results for statement 2 indicate that feedback may contain syntax that is unrelated to the algorithm. Therefore, it is necessary to improve detection accuracy by improving the detection algorithm.

6.3.2      Discussion for Experiment 2

The results of Experiment 2 confirm that logic errors can be detected by the proposed detection algorithm. In addition, we confirmed that the detection algorithm can provide appropriate feedback in many cases. Therefore, it is necessary to generalize some specific cases and to improve the algorithm.

6.3.3       Discussion for All Experiments

The results of the two experiments confirmed that the proposed algorithm can accurately detect logic errors and provide appropriate feedback. The proposed algorithm detects logic errors using source codes stored in the online judge system. To increase accuracy, we filter the codes using structure patterns and error degree. Therefore, detection accuracy depends on the diversity of source code stored in the online judge system. In the present study, although we only considered codes written in Java, the proposed algorithm can be applied to all context-free languages. There is more source code written in languages such as C and C ++, and thus logic errors can be detected with higher accuracy.

6.3.4     Improvements

In this subsubsection, we suggest some improvements based on the experimental results.

Based on the results of Experiment 1, we suggest the following two improvements. One improvement is the removal of elements not related to logic errors detected by the detection algorithm. For example, elements with the same meaning in different formats, such as variable names and logical expressions, can be removed because they are not related to logic errors. Another improvement is the use of a comparison method that is independent of the structure pattern (i.e., generalization of the algorithm). In Experiment 1, a rule regarding the structure pattern as a condition of the dataset was used. This rule was used because the LED API does not have a function for comparing source codes with different structure patterns. Therefore, we suggest generalizing the algorithm by unifying the variable declaration part and determining the format of the calculation formula. This generalization would make it possible to compare source codes with different structure patterns without changing the meaning of the algorithm.

Based on the results of Experiment 2, we suggest the following three improvements. The first improvement is a comparison method of conditional branching. The conditional branching algorithm strongly depends on the logical expression that is employed by the user. In particular, filtering by structure pattern is not effective for problems that require multiple standard outputs using conditional branching. Therefore, we suggest a comparison based on a logical expression and feedback regarding the processing order. The second improvement is a comparison method of binary expressions. Because binary expressions are parsed using certain rules, a comparison between binary expressions from different structures are not effective. Therefore, we suggest making the error degree more accurate by implementing special logic to compare binary expressions. The third improvement is a review of the weighting when the type of syntax is the same but the elements are different. As an example, method call expressions can be very different, even using the same kind of syntax.

Table 8: Results of Experiment 1

	Users		Success Users		Success Rate
Problem ID	All	Usable	Whole	Partial	Whole	Partial	Difference
ITP1_1_A	3502	358	335	358	93.58%	100.00%	+6.42%
ITP1_1_B	2425	144	110	121	76.39%	84.03%	+7.64%
ITP1_1_C	2006	187	114	142	60.96%	75.94%	+14.97%
ITP1_1_D	1618	130	86	102	66.15%	78.46%	+12.31%
ITP1_2_A	1692	291	249	263	85.57%	90.38%	+4.81%
ITP1_2_B	1525	126	106	112	84.13%	88.89%	+4.76%
ITP1_2_C	1505	87	49	74	56.32%	85.06%	+28.74%
ITP1_2_D	1194	261	93	111	35.63%	42.53%	+6.90%
ITP1_3_A	1542	270	201	208	74.44%	77.04%	+2.59%
ITP1_3_B	1405	129	108	114	83.72%	88.37%	+4.65%
ITP1_3_C	1199	63	55	57	87.30%	90.48%	+3.17%
ITP1_3_D	1059	105	92	97	87.62%	92.38%	+4.76%
ITP1_4_A	1107	315	180	252	57.14%	80.00%	+22.86%
ITP1_4_B	1134	250	157	184	62.80%	73.60%	+10.80%
ITP1_4_C	1022	14	14	14	100.00%	100.00%	0%
ITP1_4_D	909	176	107	147	60.80%	83.52%	+22.73%
ITP1_5_A	977	24	21	22	87.50%	91.67%	+4.17%
ITP1_5_B	911	33	22	26	66.67%	78.79%	+12.12%
ITP1_5_C	880	20	14	16	70.00%	80.00%	+10.00%
ITP1_5_D	968	58	51	53	87.93%	91.38%	+3.45%
ITP1_6_A	831	17	15	16	88.24%	94.12%	+5.88%
ITP1_6_B	656	15	12	14	80.00%	93.33%	+13.33%
ITP1_6_C	623	33	26	27	78.79%	81.82%	+3.03%
ITP1_6_D	566	11	9	11	81.82%	100.00%	+18.18%
ITP1_7_A	719	21	20	20	95.24%	95.24%	0%
ITP1_7_B	643	24	21	23	87.50%	95.83%	+8.33%
ITP1_7_C	595	3	3	3	100.00%	100.00%	0%
ITP1_7_D	484	66	49	64	74.24%	96.97%	+22.73%
ITP1_8_A	636	14	13	14	92.86%	100.00%	+7.14%
ITP1_8_B	591	2	0	1	0.00%	50.00%	+50.00%
ITP1_8_C	525	5	5	5	100.00%	100.00%	0%
ITP1_8_D	448	11	7	8	63.64%	72.73%	+9.09%
ITP1_9_A	518	52	35	42	67.31%	80.77%	+13.46%
ITP1_9_B	456	7	7	7	100.00%	100.00%	0%
ITP1_9_C	441	6	2	5	33.33%	83.33%	+50.00%
ITP1_9_D	323	4	4	4	100.00%	100.00%	0%
ITP1_10_A	432	32	15	22	46.88%	68.75%	+21.88%
ITP1_10_B	392	38	20	31	52.63%	81.58%	+28.95%
ITP1_10_C	458	14	9	10	64.29%	71.43%	+7.14%
ITP1_10_D	279	2	2	2	100.00%	100.00%	0%
ITP1_11_A	84	1	1	1	100.00%	100.00%	0%
ITP1_11_B	64	1	1	1	100.00%	100.00%	0%
ITP1_11_C	32	1	1	1	100.00%	100.00%	0%
ITP1_11_D	13	0	0	0	0.00%	0.00%	0%

Table 9: Results of Experiment 2

Feedback Type	Reason for Judgment	Cause of Logic Error	Rate	Total
Appropriate	Can be debugged	Literal	6.5%	80.43%
		Output format	19.6%
		Binary expression	15.2%
		Loop condition	8.7%
		Type and output format	2.2%
		Conditional branch	19.6%
		Used type	4.3%
		Used method	4.3%
Inappropriate	Direct answer	Position of variables	17.4%	19.57%
	Ignored the algorithm	Non-optimal feedback	2.2%
Wrong	Cannot be debugged		0.0%	0.0%

However, even with such a comparison, the error degree is a very small numerical value. In particular, standard output methods and various library methods are sometimes compared, so that optimal feedback cannot be generated in some cases. Therefore, we suggest measuring to what extent the syntax has the same meaning by using the namespace and arguments. We also suggest detecting the parent syntax itself as a logic error, such as when only variable names are detected as logic errors.

7. Conclusion

This study proposed a logic error detection algorithm based on structure patterns and error degree to support novice programmers. The proposed algorithm uses data in an online judge system to detect logic errors in wrong code and provides feedback for supporting problem solving. In addition, we developed the LED web API based on the proposed algorithm. The LED API is compatible with the online judge system, so it can promote autonomous learning with the corresponding environment.

Two experiments were conducted to verified the accuracy of the proposed algorithm. The experimental results show that the proposed algorithm can accurately detect logic errors and provide appropriate feedback. The proposed algorithm detected logic errors in programs for all the problems in the Introduction to Programming 1 set with high accuracy. In addition, the detection accuracy depends on the amount of data in the online judge system.

Although we constructed the autonomous learning environment and detection algorithm in Java, the proposed algorithm can be applied to various programming languages, such as C/C++, Python, and Ruby. Although the presented LED API is oriented to detec logic errors, the algorithm is capable of suggesting possible solutions. So, our future works include the extension of the API after conducting further experiments.

1.  C. B. Frey and M. A. Osborne, “The future of employment: How susceptible are jobs to computerisation?” 2013. [Online]. Avail- able: https://www.oxfordmartin.ox.ac.uk/downloads/academic/The_Future_ of_Employment.pdf
2.  I. Koichi and T. Yuta, “Digitization, Computerization, Networking, Automa- tion, and the Future of Jobs in Japan (article in Japanese with an abstract in English),” Research Institute of Economy, Trade and Industry (RIETI), Policy Discussion Papers (Japanese) 18009, May 2018. [Online].
3. Available: https://ideas.repec.org/p/eti/rpdpjp/18009.html
4.  W. E. Forum, “The future of jobs report 2018,” 2018. [Online]. Available: http://www3.weforum.org/docs/WEF_Future_of_Jobs_2018.pdf
5.  J. Gal-Ezer, C. Beeri, D. Harel, and A. Yehudai, “A high school program in computer science,” Computer, vol. 28, no. 10, pp. 73–80, Oct. 1995. [Online].
   Available: http://dx.doi.org/10.1109/2.467599
6.  S. Furber et al., “Shut down or restart? the way forward for computing in uk schools,” The Royal Society, London, 2012. [Online]. Available: https://royalsociety.org/~/media/education/computing-in-schools/ 2012-01-12-computing-in-schools.pdf
7.  Y. Okajima, “Research on the impact of compulsory programming education,”Chuo University Policy Research Institute Annual Report, no. 21/2017, pp. 203– 218, 2018-08-23. [Online]. Available: http://id.nii.ac.jp/0341/00005893
8.  K. Komatsu, “Problems and countermeasures of programming education (article in japanese),” Business review, Faculty of Business Administration, Bunkyo Gakuin University, vol. 25, no. 1, pp. 83–104, dec 2015. [Online].
9. Available: https://ci.nii.ac.jp/naid/40020853834/en/
10.  S. Furber et al., “After the reboot: computing education in uk schools,” The Royal Society, London, 2017. [Online]. Available: https://royalsociety.org/~/ media/policy/projects/computing-education/computing-education-report.pdf
11.  C. M. Intisar and Y. Watanobe, “Classification of online judge programmers based on rule extraction from self organizing feature map,” in 2018 9th Interna- tional Conference on Awareness Science and Technology (iCAST), Sep. 2018, pp. 313–318.
12.  T. Saito and Y. Watanobe, “Learning path recommender system based on re- current neural network,” in 2018 9th International Conference on Awareness Science and Technology (iCAST), Sep. 2018, pp. 324–329.
13.  C. M. Intisar and Y. Watanobe, “Cluster analysis to estimate the difficulty of programming problems,” in Proceedings of the 3rd International Conference on Applications in Information Technology(ICAIT), 2018.
14.  S. Wasik, M. Antczak, J. Badura, A. Laskowski, and T. Sternal, “A survey on online judge systems and their applications,” ACM Comput. Surv., vol. 51, no. 1, pp. 3:1–3:34, Jan. 2018. [Online]. Available: http://doi.acm.org/10.1145/3143560
15.  Y. Yoshizawa and Y. Watanobe, “Logic error detection algorithm for novice programmers based on structure pattern and error degree,” in 2018 9th Interna- tional Conference on Awareness Science and Technology (iCAST), Sep. 2018, pp. 297–301.
16.  H. Holec, Autonomy and foreign language learning. ERIC, 1979.
17.  H. Wu, Y. Liu, L. Qiu, and Y. Liu, “Online judge system and its applications in c language teaching,” in 2016 International Symposium on Educational Technology (ISET), July 2016, pp. 57–60.
18. S. Buyrukoglu, F. Batmaz, and R. Lock, “Increasing the similarity of program- ming code structures to accelerate the marking process in a new semi-automated assessment approach,” in 2016 11th International Conference on Computer Science Education (ICCSE), Aug 2016, pp. 371–376.
19.  E. Stankov, M. Jovanov, B. Kostadinov, and A. M. Bogdanova, “A new model for collaborative learning of programming using source code similarity detec- tion,” in 2015 IEEE Global Engineering Education Conference (EDUCON), March 2015, pp. 709–715.
20.  Y. Teshima and Y. Watanobe, “Bug detection based on lstm networks and solution codes,” in 2018 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Oct 2018, pp. 3541–3546.
21.  X. Su, J. Qiu, T. Wang, and L. Zhao, “Optimization and improvements of a moodle-based online learning system for c programming,” in 2016 IEEE Frontiers in Education Conference (FIE), Oct 2016, pp. 1–8.
22.  E. Araujo, M. Gaudencio, D. Serey, and J. Figueiredo, “Applying spectrum- based fault localization on novice’s programs,” in 2016 IEEE Frontiers in Education Conference (FIE), Oct 2016, pp. 1–8.
23.  T. Nguyen and C. Chua, “A logical error detector for novice php programmers,” in 2014 IEEE Symposium on Visual Languages and Human-Centric Computing (VL/HCC), July 2014, pp. 215–216.
24.  K. K. Sharma, K. Banerjee, I. Vikas, and C. Mandal, “Automated checking of the violation of precedence of conditions in else-if constructs in students’ programs,” in 2014 IEEE International Conference on MOOC, Innovation and Technology in Education (MITE), Dec 2014, pp. 201–204.
25.  H. Blau, S. Kolovson, W. R. Adrion, and R. Moll, “Automated style feedback for advanced beginner java programmers,” in 2016 IEEE Frontiers in Education Conference (FIE), Oct 2016, pp. 1–9.
26. J. Feng, B. Cui, and K. Xia, “A code comparison algorithm based on ast for plagiarism detection,” in 2013 Fourth International Conference on Emerging Intelligent Data and Web Technologies, Sept 2013, pp. 393–397.
27.  G. Tao, D. Guowei, Q. Hu, and C. Baojiang, “Improved plagiarism detection algorithm based on abstract syntax tree,” in 2013 Fourth International Con- ference on Emerging Intelligent Data and Web Technologies, Sept 2013, pp. 714–719.
28.  Y. Zhang, X. Gao, C. Bian, D. Ma, and B. Cui, “Homologous detection based on text, token and abstract syntax tree comparison,” in 2010 IEEE International Conference on Information Theory and Information Security, Dec 2010, pp. 70–75.
29. Y. Watanobe, “Development and operation of an online judge system,” Information Processing, vol. 56, no. 10, pp. 998–1005, sep 2015. [Online]. Available: https://ci.nii.ac.jp/naid/4002059103

(Click Here)

(Click Here)