1. Introduction

This paper is an extension of the work originally presented in the 2017 6th IEEE International Conference on Advanced Logistics and Transport (ICALT) in [1]. Loss of logistics efficiency becomes the highest across the supply chain at the nearest point to the aggregated or single demand point [2, 3].  This last (or sometimes first) mile logistics face significant fulfillment constraints, making it the most expensive part of the overall supply chain. For a company that moves millions of tons of materials every year, reducing the last mile logistics cost by a few cents can save tremendous amounts of money. As such, the company looks for new strategies to reduce the last mile logistics cost. Several strategies such as a horizontal collaboration with other similar companies or partners in the same level of the supply chain are now attracting the interest of those companies  [4, 5, 6].

In supply chain, collaborations between companies can be grouped into two, namely: vertical and horizontal collaboration [7]. The vertical collaboration includes collaboration between companies in different level of supply chain [7], such as  Vendor Managed Consignment Inventory (VMCI) model [8] and Collaborative, Planning, Forecasting and Replenishment (CPFR) model [9]. While the horizontal collaboration includes two or more unrelated or competing companies at the same level of the supply chain [7]. In horizontal collaboration, a company can work closely with another company that has similar logistic requirements by sharing resources and taking advantage of potential distribution synergies [10]. The benefits of horizontal collaboration are increasing vehicle utilization on the main tracking routes and vehicle efficiency as well as better improving resource management and delivery service level to the customers. Although vertical collaboration has been deeply studied and implemented [11], horizontal collaboration is still in its infancy [12, 13].

As illustrated in Figure 1, horizontal collaboration can be done in several forms. A company may explore the option of engaging one or more companies (e.g. Logistics Service Provider (LSP)) in a form of fixed outsourcing contracts to fulfill its last mile logistics demands. The company may need to guarantee a certain number of logistics demands or usage for a fixed period of time (e.g. monthly, quarterly or yearly) to the outsourcing companies. Using outsourcing, the company is able to save a substantial amount of money because the company does not need to invest in costly logistics-related assets such as transportation vehicles. Generally, this kind of outsourcing would incur a certain amount of fixed transportation and logistics costs.

For a company who has more fluctuated logistics demands, it would be difficult to guarantee a certain number of logistics demands or usage for outsourcing mechanism. The company may need to pay the fixed cost even though it has minimum logistics demands. For this kind of company, a model with a flexible (and often less binding) agreement, such as “uberization” and “4th party milk run” (4PMR) would be beneficial. These models use the pay-per-use mechanism that allows the company to pay only based on its logistics demands. It would reduce the logistics cost by translating the fixed costs to marginal costs. For example, the company does not need to pay fixed cost of 90,000/month for having only 50 last mile logistics demands.

These models use sharing economy concept to reduce the transportation costs. Uberization mainly focuses on conducting the deliveries using crowdsourcing, while the 4PMR model focuses on collaborating with one company (B2B) that has existing delivery routes/networks along the last mile delivery locations.

This paper focuses on analyzing the 4PMR model for reducing last mile logistics cost. It extends the model in [1, 14]. The 4PMR model is developed as an optimization model and solved using two metaheuristics solvers/algorithms. To investigate the cost reduction, we test the model on two scenarios. The first scenario is a hypothetical scenario based on our field study in Jakarta, Indonesia. It consists of 40 random logistics demand samples. While the second scenario is an actual scenario based on 9,622 logistics demands from an LSP in Surabaya, Indonesia. Our experiment results show that the 4PMR model is able to reduce 4.16% and 24.84% of the logistics cost in the first and the second scenario respectively. This provides a promising indication that the 4PMR model would be able to reduce the last mile logistics cost. To complement the experiment results, we also gather industry perspectives for implementing the 4PMR model in its day-to-day logistics operations.

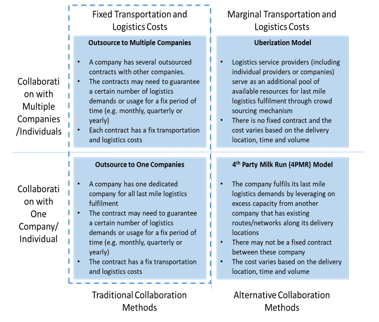Figure 1. Horizontal Collaboration Strategies

The remainder of the paper is organized as follows. Section 2 presents the overview of 4PMR and its related works. Section 3 reviews the 4PMR optimization model. Section 4 describes the solvers/algorithms to solve the 4PMR and section 5 describes the computational experiments, including the scenarios and experiment results. Section 6 reviews the industry perspective on implementing 4PMR model. Lastly, section 7 presents the conclusions.

2. 4^th Party Milk Run (4PMR) Model

2.1.  Overview

The 4PMR model leverages on the excess capacities from one company that has existing designated routes along the last mile logistics demand locations of another company. The company with existing designated routes (henceforth as providing company) needs to serve those routes periodically regardless of the delivery volume. These routes may not be fully utilized and may have significant excess capacities. These unused capacities can be tapped and used by another company (henceforth as receiving company) to fulfill its last mile logistics demands.

In 4PMR model, the routing is based on the existing routes or networks from the providing company. It would stop at several locations to fulfill logistics demands from the receiving company.

2.2.  Benefits of 4PMR model

The 4PMR model would bring benefits to the collaborating companies. These benefits can be categorized into three groups: costs and productivity, service and market position.

1. Cost and productivity benefits

One potential benefit of using the 4PMR model is to reduce logistics costs [15, 16]. Both collaborating companies, providing and receiving companies, would be able to achieve logistics cost reduction. By joining their delivery requirements, these companies can utilize and optimize their logistics-related assets. This can be translated into a lower logistics cost and lower capital investment for logistics-related assets as it would need a lesser number of logistics-related assets.

One example of this cost reduction is on empty backhaul utilization. The providing company may have existing routes from area A to area B. If there is an imbalance of deliveries where all the loads come from area A to area B with no loads from area B to area A, the providing company must absorb the cost of the empty vehicle return (empty backhauls). However, if another company has last mile logistics demands in the opposite direction (from area B to area A), the company can make use of the empty backhauls. The providing company would be able to reduce its costs of absorbing empty backhaul while the receiving company would be able to negotiate a lower transportation cost.

2. Service benefits

For the receiving company, the 4PMR model would add the company capabilities to serve low demand areas. It allows the company to facilitate more frequent deliveries for wider geographic areas. The receiving company would be able to expand its area coverage by collaborating with the providing company that operates in different areas with minimum additional setup cost. It provides flexibility in providing more service and reaching more potential customers.

3.  Market Position

For the providing company, the 4PMR model would enable the company to have “insinking” opportunities where the company would be able to replicate its 4PMR model to provide services to different companies and proactively select a group of companies with a strong synergy potential [10, 17]. It would create another business opportunity for the providing company. It would further increase vehicle utilization and reduce the last mile logistics cost.

2.3.  Related Works

Two areas of works that is closely related to ours are the Vehicle Routing Problem (VRP) [18, 19] and Milk Run Logistics [20, 21]. VRP aims to provide optimal set of routes for a fleet of vehicles to fulfil logistics demands. It has many variants, including VRP with Time Windows [22, 23], Capacitated VRP [24, 25], green VRP [26, 27] and ride-sharing VRP [28, 29]. While Milk Run Logistics is essentially a logistics method that uses routing to consolidate the transportation of goods that has the following characteristics: small lot of transport, less than truckload, geographically sparse demands [20], as illustrated in Figure 2. As shown in Figure 2, milk run model reduces the excess capacity by consolidating the deliveries from different companies (i.e. Company X and Company Y).

3. Optimization Model

One potential concern with the 4PMR model is that the providing company may not have a direct route to fulfill the receiving company’ logistics demands (direct from an origin location to a final destination location). It may need to go through several stops/hops/transit locations before it can finally deliver to the final delivery destination.  There is a need to match the providing company existing routes with the receiving company logistics demand locations.

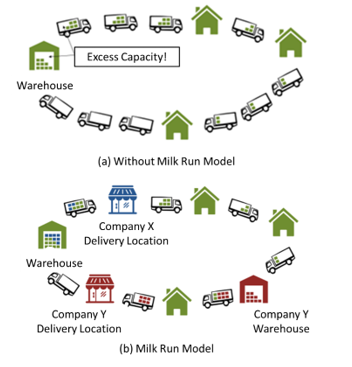Figure 2. Milk Run Model Illustration

To match the logistics demands with the existing routes, an optimization model for the 4PMR is developed. The 4PMR model is defined as follows. Let  be a directed graph representing the providing company existing routes. It consists of a set of locations, as vertexes or nodes (the term vertex and node are used synonymously throughout the paper), denoted by , and a set of routes, as arcs E Í V x V, denoted by an ordered pair of nodes (u, v), where  and .  represents a directed route from node u to node v. Each arc  has an excess capacity  and time capacity . To simplify the problem, we consider each arc to have a fixed excess capacity . For each arc , ,  and represent a non-negative travel distance, a non-negative travel time and a non-negative transportation cost for arc , respectively. A path is defined as a sequence of arc .

Let  be a set of logistics demands of the receiving company. Each delivery  has delivery load size , origin node u  and destination node v.  denotes the time window in origin node u. While  denotes the time window in destination node v. Each delivery service at origin node u and destination node v must take place between the time windows.  For each logistics demand  from origin node u to destination node v fulfilled by 4PMR model, the delivery cost is defined as , where  If the delivery fulfillment cannot be done using the 4PMR model (due to capacity or time constraints), it will use a direct delivery. The delivery cost for the direct delivery denotes as , where in general .

There are a lot of constraints that can be included in the 4PMR model, such as capacity, transportation cost, overall cost, transportation distance, and time windows. These constraints depend on the nature of the collaboration between providing and receiving companies and the nature of the products being delivered. In this paper, we only use one constraint, capacity. The capacity for logistics demands fulfilled by the 4PMR should not exceed the fixed weight capacity for each arc. The model can be expended to include more constraints.

Using these notations, we define the 4PMR problem as:

Constraint (2) and (3) ensures that the capacity for logistics demands fulfilled by the 4PMR model goes through a certain arc should not exceed the fixed weight capacity for that arc.

4. Solvers and Algorithms

The 4PMR optimization model is implemented in two solvers/algorithms. The first solver is designed for a small dataset with less than 50 logistics demands. It uses an evolutionary function in Microsoft Excel [30]. The function is based on genetic and evolutionary algorithm to seek “good” solutions for a limited dataset. This solver fits the purpose to provide a preliminary result for further study and exploration.

The second solver is used for large problem sizes. It is developed using a meta-heuristic algorithm that combines the Dijkstra algorithm with the Greedy algorithm [31]. The algorithm has two parts as illustrated in Figure 3. First, it uses the Dijkstra algorithm to produce all the shortest paths for each pair of delivery locations in the existing routes. It also calculates the logistics cost for each of the shortest path. Second, it runs the greedy algorithm to assign the logistics demands to the path with minimum cost. It will also re-configure the shortest paths and re-calculate the logistics cost, if necessary.

Figure 3. Meta-Heuristics Algorithm for Solving 4PMR

5. Computational Experiments

5.1.  Small Problem Size

The 4PMR model was tested on a hypothetical scenario based on our field study in Jakarta, Indonesia in December 2016. The scenario comprises of a providing company with 5 existing routes. The routes connect 12 nodes. In each route, the delivery starts from and returns to the providing company’ warehouse. The logistics demands are derived from a receiving company with 40 logistics demands in several locations along the providing company’s routes. The receiving company produces goods and uses a hub-and-spoke model to deliver goods to all its customers within the same distribution network. The receiving company has a headquarter/main warehouse for its hub-and-spoke model. The providing company’s warehouse and the receiving company’s headquarter are located in different locations (represented by different nodes).

Given that the logistics demands originating from the receiving company, all the logistics demands share the same origin point – the receiving company’s headquarter.  For the hub and spoke distribution network, the utilization of the vehicles is 80% and that they return back to headquarter empty.

We run the first solver for this scenario. The experiment results are shown in Table 1. The results show that the 4PMR model is able to get a 4.16% reduction for the receiving company. For the no collaboration (own vehicle) model, the company will have additional costs to purchase the vehicles also (which is not included in the comparison). The detailed results for this experiment can be found in [1].

Table 1. Experiment Result of the 4PMR Model in Small Problem Size

Solution	Parameters
	Total number of logistics demands	Number of logistics demands using 4PMR model	Logistics Cost
No collaboration (own vehicle)*	40	0	56.737
The 4PMR model	40	11	54.377

*: only logistics cost, without capital cost to purchase the vehicles

5.2.  Experiment Result in Large Problem Size

To evaluate the performance of the 4PMR model in large problem size, we tested the model on scenario based on actual delivery routes from one Logistics Service Provider (LSP) in Surabaya, Indonesia. The LSP has an existing network comprising 27 nodes/locations with existing routes in Greater Surabaya, Indonesia. Each route has a certain excess capacity (around 20% of the overall capacity). The logistics demands were derived from real logistics demands from one FMCG company operated in Surabaya, Indonesia. We used 10 days of logistics demands in July 2015. It comprises of 9,622 logistics demands for different locations in Greater Surabaya.

Using the second solver, we run the 4PMR model for this scenario. In our experiment, we set the processing (i.e. execution) time to 10 second. To compare the 4PMR model with another horizontal collaboration, we also calculated the transportation cost for outsource mechanism. We assumed that the company needs to pay for 1 dollar for each delivery with minimum delivery of 1,000 deliveries/day.

The experiment results are shown in Table 2. The results show that the 4PMR model is able to get a 24.84% reduction from the no collaboration model and 29.54% reduction from the outsource model. For the no collaboration (own vehicle) model, the company will have additional costs to purchase the vehicles also (which is not included in the comparison).

6. Industry Perspective in Implementing 4PMR

While the benefits of the 4PMR model are clear, implementing it can be challenging. The challenges are varied depending on the company and also the industry. Based on our observation and close interaction with one e-commerce company in Singapore, we observe these two main challenges.

Table 2. Experiment Result of the 4PMR Model in Large Problem Size

Solution	Parameters
	Total number of logistics demands	Number of logistics demands using 4PMR model	Logistics Cost
No collaboration (own vehicle)*	9,622	0	9,622.0
Horizontal collaboration with outsource	9,622	0	10,264
With 4PMR	9,622	2,656	7,231.6

*: only logistics cost, without capital cost to purchase the vehicles

Firstly, stakeholders of the 4PMR model (i.e. providing and receiving company) will require access to as much real-time data as possible. The providing company needs to provide information about its routes and excess capacities so that the receiving company can decide on whether to utilize those excess capacities or not. When excess capacities are eventually bought up, the providing company then has to update its information again to show the latest excess capacities and the routes to fulfill the receiving company’s last mile logistics demands. Hence, software that leverages on secure and real-time data is needed. The Internet and the Internet of Things (IoT) can be used to facilitate information sharing (e.g. mobile applications to link providing and receiving companies).

For the providing company with existing the Transportation Management Software (TMS), another challenge will be to integrate the 4PMR solver/algorithm with its TMS. As TMS typically captures information about the vehicle, the cargo, the route and schedule, the logistics demands using the 4PMR model should be updated to the company’s TMS.

Secondly, potential stakeholders of the 4PMR model (i.e. potential providing and receiving company) need to be convinced about the benefits of the 4PMR model. The potential providing company needs to evaluate whether the effort both in terms of IT infrastructure changes and manpower training to improve excess capacities worthwhile and whether there is an obvious return on investment. The potential receiving company needs to analyze its last mile logistics requirements and decides if the 4PMR model would be able to fulfill its business needs. For example, if a company requires trucking of large volumes (typically half to full truckload), it needs to understand that it risks its deliveries for not being fulfilled by the providing company because there are simply not enough excess capacities. Alternatively, if a company requires frequent trucking of easily forecasted volumes, it may need to evaluate the 4PMR model cost versus the traditional outsource model.

7. Summary and Key Take Away

This paper introduces the 4^th Party Milk Run (4PMR) model for collaboration between similar companies in the same level of the supply chain. The 4PMR model leverages the excess capacities from one company (i.e. providing company) that has existing designated routes along the pick-up and delivery locations of another company (i.e. receiving company). The providing company needs to serve those routes periodically regardless of the delivery volume, and often these deliveries are not at full capacity. These unused capacities can be tapped and used by the receiving company to fulfill its last mile logistics needs. It would potentially bring benefits to the companies involved in terms of costs and productivity, service and market position.

Two solvers are designed to implement the 4PMR model. The solvers aim to match the providing company’s existing routes with the receiving company’s logistics demands. The first solver is used for small problem size scenario, while the second solver is used for large problem size scenario. We run these solvers for two scenarios – a small problem size scenario and a large problem size scenario. From the experimental result, it is also revealed that 4PMR is able to reduce logistics cost for up to 4.16% (in the small problem size scenario) and 24.84% (in the large problem size scenario).

Conflict of Interest

The authors declare no conflict of interest related to this paper.

1.  C. Lee, Lindawati and R. de Souza, “Utilizing Excess Capacity in Last Mile Using 4th Party Milk Run,” in 6th IEEE International Conference on Advanced Logistics and Transport, Bali, Indonesia, 2017.
2.  R. de Souza, M. Goh, H. Lau, W. Ng and P. Tan, “Collaborative urban logistics–synchronizing the last mile a Singapore research perspective,” Procedia-Social and Behavioral Sciences, vol. 125, pp. 422-431, 2014.
3.  J. Lin, Q. Chen and K. Kawamura, “Sustainability SI: logistics cost and environmental impact analyses of urban delivery consolidation strategies,” Networks and Spatial Economics, vol. 16, no. 1, pp. 227-253, 2016.
4.  I. Badraoui, J. G. Van der Vorst and Y. Boulaksil, “Horizontal logistics collaboration: an exploratory study in Morocco’s agri-food supply chains,” International Journal of Logistics research and applications, pp. 1-18, 2019.
5.  Y. Sheffi, M. J. Saenz, L. Rivera and D. Gligor, “ew forms of partnership: the role of logistics clusters in facilitating horizontal collaboration mechanisms,” European Planning Studies, pp. 1-26, 2019.
6. N. Martin, L. Verdonck, A. Caris and B. Depaire, “Horizontal collaboration in logistics: decision framework and typology,” Operations Management Research, vol. 11, no. 1-2, pp. 1-19, 2018.
7.  L. Chen, X. Zhao, O. Tang, L. Price, S. Zhang and W. Zhu, “Supply chain collaboration for sustainability: A literature review and future research agenda,” nternational Journal of Production Economics, vol. 194, pp. 73-87, 2017.
8.  M. Hariga, S. Babekian and Z. Bahroun, “Operational and environmental decisions for a two-stage supply chain under vendor managed consignment inventory partnership,” International Journal of Production Research, vol. 57, no. 11, pp. 3642-3662, 2019.
9.  C. A. Hill, G. P. Zhang and K. E. Miller, “Collaborative planning, forecasting, and replenishment & firm performance: An empirical evaluation,” International journal of production economics, vol. 196, pp. 12-23, 2018.
10.  F. Cruijssen, P. Borm, H. Fleuren and H. Hamers, “Supplier-initiated outsourcing: A methodology to exploit synergy in transportation,” European Journal of Operational Research, vol. 207, no. 2, pp. 763-774, 2010.
11.  S.-L. D., P. Kaminsky and E. Simchi-Levi, Designing and Managing the Supply Chain: Concepts. Strategies, and Cases, McGraw-Hill, 2000.
12.  F. Cruijssen, W. Dullaert and H. Fleuren, “Horizontal cooperation in transport and logistics: a literature review,” Transportation journal, pp. 22-39, 2007.
13.  R. Leitner, F. Meizer, M. Prochazka and W. Sihn, “Structural concepts for horizontal cooperation to increase efficiency in logistics,” CIRP Journal of Manufacturing Science and Technology, vol. 4, no. 3, pp. 332-337, 2011.
14.  The Logistics Institute – Asia Pacific, “E-Commerce Trends and Challenges: A Logistics and Supply Chain Perspective,” The Logistics Institute – Asia Pacific White Papers Series, Singapore, 2016.
15.  L. Wang, F. Kong, J. Cao and Y. Wang, “Research on the application and optimization countermeasures of auto parts milk-run logistics mode,” in IEEE 18th International Conference on Industrial Engineering and Engineering Management, 2011.
16.  M. Jafari-Eskandari, S. Sadjadi, M. Jabalameli and A. Bozorgi-Amiri, “A robust optimization approach for the milk run problem (An auto industry Supply Chain Case Study),” in IEEE International Conference on Computers & Industrial Engineering, 2009.
17.  F. Cruijssen, B. Peter, H. Fleuren and H. Hamers, “Insinking: A Methodology to Exploit Synergy in Transportation,” CentER Discussion Paper, 2005. [Online]. Available: https://ssrn.com/abstract=870403. [Accessed 26 03 2018].
18.  P. Toth and D. Vigo, The vehicle routing problem, Philadelphia: Society for Industrial and Applied Mathematics, 2002.
19.  B. L. Golden, S. Raghavan and E. A. Wasil, he vehicle routing problem: latest advances and new challenges, New York: Springer Science & Business Media, 2008.
20.  G. Brar and G. Saini, “Milk run logistics: literature review and directions,” Proceedings of the world congress on engineering, vol. 1, pp. 6-8, 2011.
21.  G. S. Brar and G. Saini, “Milk run logistics: literature review and directions,” in In Proceedings of the world congress on engineering, 2011.
22.  F. Errico, G. Desaulniers, M. Gendreau, W. Rei and L. M. Rousseau, “The vehicle routing problem with hard time windows and stochastic service times,” EURO Journal on Transportation and Logistics, vol. 7, no. 3, pp. 223-251, 2018.
23.  Y. Niu, Z. Yang, P. Chen and J. Xiao, “Optimizing the green open vehicle routing problem with time windows by minimizing comprehensive routing cost,” Journal of cleaner production, vol. 171, pp. 962-971, 2018.
24.  L. Wei, Z. Zhang, D. Zhang and S. C. Leung, “A simulated annealing algorithm for the capacitated vehicle routing problem with two-dimensional loading constraints,” European Journal of Operational Research, vol. 265, no. 3, pp. 843-859, 2018.
25.  A. N. Letchford and J. J. Salazar-González, “The capacitated vehicle routing problem: stronger bounds in pseudo-polynomial time,” European Journal of Operational Research, vol. 272, no. 1, pp. 24-31, 2019.
26.  G. Poonthalir and R. Nadarajan, “A fuel efficient green vehicle routing problem with varying speed constraint (F-GVRP),” Expert Systems with Applications, vol. 100, pp. 131-144, 2018.
27.  A. Shuib and N. Muhamad, “Mixed Integer Multi-Objective Goal Programming Model For Green Capacitated Vehicle Routing Problem,” Advances in Transportation and Logistics Research, vol. 1, no. 1, pp. 356-368, 2018.
28.  L. Agussurja, S. F. Cheng and H. C. Lau, “A State Aggregation Approach for Stochastic Multiperiod Last-Mile Ride-Sharing Problems,” Transportation Science, vol. 53, no. 1, pp. 148-166, 2019.
29.  V. F. Yu, S. S. Purwanti, A. P. Redi, C. C. Lu, S. Suprayogi and P. Jewpanya, “Simulated annealing heuristic for the general share-a-ride problem,” Engineering Optimization, vol. 50, no. 7, pp. 1178-1197, 2018.
30.  FrontlineSolvers, “Excel Solver – Non-smooth Optimization,” [Online]. Available: http://www.solver.com/excel-solver-non-smooth-optimization. [Accessed 01 05 2017].
31. A. Benoit, R. Yves and F. Vivien, A guide to algorithm design: paradigms, methods, and complexity analysis, Boca Raton: CRC Press, 2013.

(Click Here)

(Click Here)