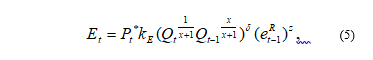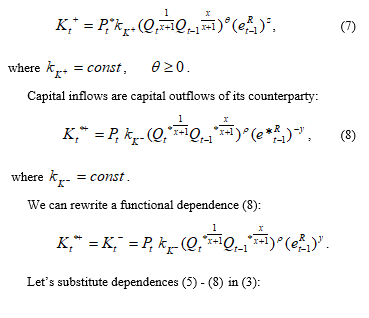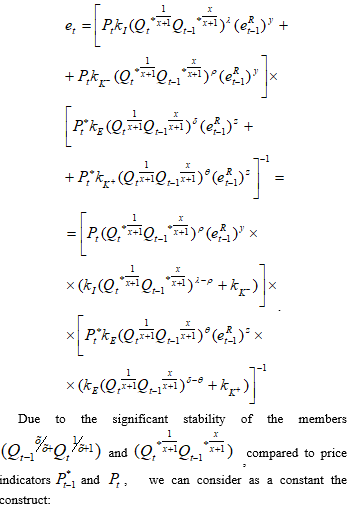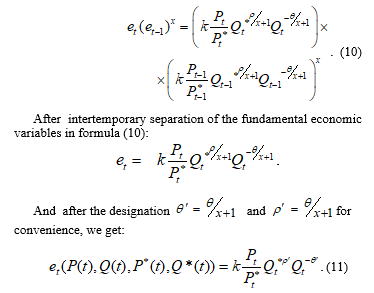Exchange Rate Modeling: Medium-Term Equilibrium Dynamics
Adv. Sci. Technol. Eng. Syst. J. 4(4), 251–255 (2019);
DOI: 10.25046/aj040431
In this study, we develop the author’s approach, based on the principles of modeling of the International Flows Equilibrium Exchange Rate (IFEER). As a result, a new model is built, depending on the main macroeconomic factors in the medium term. The model presents a wide system of basic factors, but many of the intermediate factors in the modeling were eliminated. The results are discussed in the context of the previously known results of economic theory.
1. Introduction
This paper is an extension of work originally presented in Eleventh International Conference “Management of large-scale system development” (MLSD 2018, IEEE Russian section) [1] .
In the scientific literature the nominal and real exchange rate models are widely represented in conditions of the dynamic general equilibrium (DSGE-models), the founders of which is the model Obstfeld-Rogoff [2] of monopolistic competition of two open economies. At the same time, the previous approaches to fundamental factors modeling were developed by Mussa [3] and Dornbush [4] in conditions of both the monetarist and Keynesian approaches.
Many authors emphasizes the effectiveness of fundamental factors models of nominal and real exchange rates (e.g., [5]).
Conditions for the existence of the equilibrium rates were allocated in 1945 by R. Nurkse [6], which paid considerable attention to the balance of payments equilibrium, the lack of restrictions on export-import operations and capital flows and internal stability of the economy.
However, from the standpoint of structural modeling, the known models of economic theory cannot provide adequate results for assessing of the equilibrium real or nominal rates level. In a significant majority the exchange rates are not expressed in terms of the equilibrium of the financial market, but in terms of the theory of purchasing power parity (PPP). Structurally, the exchange rate analysis is limited by the current balance. Herewith, it should be emphasized the role of the exchange rates in the process of regulating the external balances and the role of the indicator of competitive advantages in foreign trade flows.
To solve these problems, we propose to use the author’s approach, based on the principles of the international flows equilibrium exchange rate (IFEER) modeling [1, 7].
2. Conceptual Bases of Modeling
It should be noted, that in this article we develop the IFEER-approach and the new equilibrium exchange rate model will be presented as a result.
Initially, we suppose that the world consists of two equal rights open economies and international trade flows take into account the trading competitive position of these countries. In this context, international trading bilateral competitive position is determined by the real exchange rate. It should be noted here, that approach “small open economy – the rest of thе world” under IFEER-concept was used by the author in modeling of the Russian ruble exchange rate (e.g., [7]).
We consider all real market transactions at nominal exchange rates on the domestic currency market that occurred in a certain period of time.
Then in i-th transaction are: the bilateral nominal exchange rate, the amount in the determined foreign currency and the amount in the national currency respectively.
In this context, these variables are linked by ratios:
, and therefore, .
So, we define the synthetic value of the bilateral nominal exchange rate in conditions of varying degrees of free floating for the certain period as the sum of exchange rates, weighted by amounts in determined foreign currencies:
where – the demand in the national currency on imports,
– the supply in the foreign currency from exports,
– the capital inflows in the foreign currency,
– capital outflows in the national currency.
This formula takes into account such important components as export revenue, demand for imports, demand for foreign assets and so on.
Therefore,we are developing two-period model in the dynamics in times t and t-1.
Herewith, at time t value of the functions of export-import operations and capital flows will be directly determined by the international competitive position represented by the real exchange rate at the time t-1:
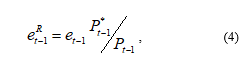where – the exernal prices index,
– the internal prices index.
For the model verification the price indices can be represented by consumer prices index (CPI), GDP-deflator and so on.
In the analysis of exchange rates, many authors (e.g., М. Bahmani-Oskoee and G. Goswami [8]) determine the terms of trade, reflecting the effectiveness of export-import operations in world trade, as one of the determining factors of the dynamics.
For example, F. Caramazza [9] explored the expectations of investors of German mark against French franc dynamics – one of the main cross-rates in the world at that time. He explained the change in parity by largely fundamental macro-variables, including terms of trade and relative inflation differential. L. Bartolini [10] similarly revealed the relationship between market expectations of devaluation and CPI-indicator of trading international advantages.
In the author’s model of the ruble exchange rate [11], the use of trade terms by micro-agents as the main determinant of foreign trade operations is proved and justified on the statistical series of import and export of Russia. However, they are expressed in adjusted nominal exchange rates at price levels, including actual export prices.
3. Exchange Rate Modeling: Medium-Term Equilibrium Dynamics
In the domestic foreign exchange market at time t export earnings as part of the average real gross domestic output in foreign prices depend on the decision of producers-exporters and the state of international trade conditions at time t-1:
where
– real gross domestic output.
In a function (5) says, that the produced exports are part of averaged real gross domestic output (e.g., real GDP).
Due to the stability , the averaging method does not give a significant contribution to the fluctuations of the functional dependence (5).
The parameter z is the response to change in international trading position and the index x is associated with indexes z and y in the functions (5) and (6): x=(z-y).
In a functional dependence (5) the parameter reflects the fact that the growth rate of export exceeds the growth of gross domestic product because of a limitation of domestic demand: .
In the framework of the simulation because of equal rights and symmetry of flows the export of a country is an import of counterparty.
By analogy with a functional dependence (5):
As can be seen from formula (3), capital flows and export-import operations directly affect the exchange rate dynamics.
It should be noted that many well-known models of economic theory have serious difficulties with formalizing of the impact of capital flows on the exchange rates. However, within the framework of the proposed IFEER-concept, we can directly determine these functional dependencies.
At the same time, the mechanism of formation of functional dependencies of capital flows is very similar to the mechanisms of formation of export-import operations regarding the chosen factor system. More details can be found in the author’s work [1]. For example, at time t we suppose that non-residents buy part of the real averaged domestic product in their prices:
4. Setting the Model Parameters and Verification
The starting point of the study of the medium-term exchange rate dynamics should be characterized by stability, both internal and external economic situation. More details can be found in the author’s work [1].
We suggest that setting of the parameters and can use the least squares method with a normalized differences of the nominal theoretical and nominal market exchange rates under constraints and :
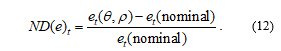At the starting point of the selected period it must be put: P(start)=1, Q(start)=1, P*(start)=1, Q*(start)=1. Coefficient k must be equal to the nominal market exchange rate at the starting point.
Next, the sum of normalized squared deviations (12) minimizes:
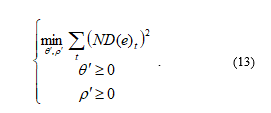In order to verify the model, it is advisable to consider the results in the context of the known results of economic theory of determination of the exchange rates.
For these intentions, let us rewrite formula (11) in logarithms:
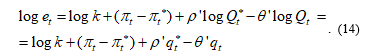Using the I.Fischer equation PQ=MV, where M is the money supply, V is the velocity of money, we present this in logarithms: .
Assuming in the medium term the rate of the velocity of money is constant and substituting (14) symmetrically for both countries, we obtain (with )
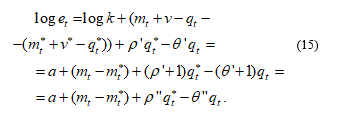Verification of dependencies of a similar type (15), having the same system of fundamental macroeconomic factors, has been successful within the framework of verification of the monetary model. Of the works on this topic it should be noted econometric studies of models of fundamental determinants of B. R. Clarida et al. [12], J. Cheung, M. Chinn, and A. Pascual [13], I. Chowdhury [14].
It is also interesting to consider predictive abilities of dependencies of a similar type. One of the most famous is the study of J. Chen and N. Mark [15]. The forecasts for the formula of type (15) at on different time horizons gave a significantly better result than in accordance with a random walk. And it was in the medium and long term.
5. Results and Conclusion
Exogenous variables are the total products Q and Q* and the levels of external and internal prices P*, P in the countries of the bilateral exchange rate in this model. Other basic intermediate determinants, such as export-import operations, capital flows, the terms of trade in the modelling process have been eliminated.
It should be noted here, that author’s IFEER-concept of Equilibrium Exchange Rate (EER) correlates with the widely known economical concepts: behavioural EER (BEER) [16, 17] and fundamental EER (FEER) [18].
Using national consumer price and real domestic product indices and oil prices, the main research formula (11) was applied by the author to the study of the dynamics of the Russian ruble against the US dollar in the period 2013-2015. The results of econometric verification showed a very high quality of the model.
Thus, we can state the high practicality of models of fundamental determinants in relation to different currency pairs, based on both “real” (Russian ruble, US dollar, Canadian dollar, etc.) and “past” (German mark, French franc) currencies.
Conflict of Interest
The author declares no conflict of interest.
- A. Kuzmin, “Equilibrium Exchange Rate Modeling” in Eleventh International Conference “Management of large-scale system development” (MLSD 2018), Moscow, Russian Federation, https://ieeexplore.ieee.org/document/8551843/metrics#metrics, Publisher: IEEE, 2018, Electronic ISBN: 978-1-5386-4924-4. DOI: 10.1109/MLSD.2018.8551843.
- M. Obstfeld, K. Rogoff, “Exchange Rate Dynamics Redux” Journal of Political Economy, 103( 3), 624-660, 1995.
- R. Dornbush, “Expectations and Exchange Rates Dynamics” Journal of Political Economy, Vol.84, December, 1161-1176, 1976.
- M. Mussa, “The Exchange Rate, the Balance of Payments and Monetary and Fiscal Policy Under Regime of Controlled Floating” Scandinavian Journal of Economics, May, 78 (2), 229-248, 1976.
- C.M. Engel, N.C. Mark and K.D. West, Exchange Rate Models Are Not As Bad As You Think, NBER Macroeconomics Annual, Vol. 22, 2007, revised in 2011.
- R. Nurkse, Conditions of International Monetary Equilibrium, 1945 in The International Monetary System: Highlights from Fifty Years of Princeton’s Essays in International Finance, Kenen P.B. (ed.), Boulder, Colorado: Westvie Press, 1993.
- A. Kuzmin, “Exchange Rate Modeling: The Case of Ruble” Review of Business and Economics Studies, 3(3), 39-48, 2015.
- M. Bahmani-Oskoee, G. Goswami, “Exchange Rate Sensitivity of Japan’s Bilateral Trade Flows” Japan and the world economy, 16(1), 1–15, 2004.
- L. Bartolini, Devaluation and Competitiveness in a Small Open Economy: Ireland 1987-1993, IMF Working Paper WP/93/82, Washington: IMF, November, 1993.
- F. Caramazza, French-German Interest Rate Differentials and Time-Varying Realignment Risk, Washington: IMF Staff Papers, Vol.40, September, 1993.
- A. Kuzmin, “A Structural Model of Exchange Rate Dynamics” Review of Business and Economics Studies, 2(3), 86-92, 2014.
- R. H. Clarida, L. Sarno, M.P. Taylor, G. Valente, The Out-of Sample Success of Term Structure Models as Exchange Rate Predictors: A Step Beyond, NBER Working Paper, No 8601, Cambridge, Massachusetts: National Bureau of Economic Research , 2001.
- Y.-W. Cheung, M. Chinn, A.G. Pascual, Empirical Exchange Rate models: Are any Fit to Survive?, IMF Working Paper WP/04/73, Washington: IMF, 2004.
- I. Chowdhury, “Sources of Exchange Rate fluctuation: empirical evidence from six emerging market countries” Applied Financial Economics, 14(1), 697-705, 2004.
- J. Chen, N.C. Mark, “Alternative Long-Horizon Exchange-Rate Predictors“ International Journal of Finance and Economics, 1, 229–250, 1996.
- P.B. Clark, R. MacDonald, Exchange Rates and Economic Fundamentals: A Methodological Comparison of BEERs and FEERs, IMF Working Paper 98/67, Washington: International Monetary Fund, March, 1998.
- P.B. Clark, R. MacDonald, Filtering the BEER a permanent and transitory decomposition, IMF Working Paper 00/144 – Washington: International Monetary Fund, 2000.
- J. Williamson, Estimates of FEERs, In Estimating Equilibrium Exchange Rates, Williamson J. (ed.), Washington: Institute for International Economics, 1994.