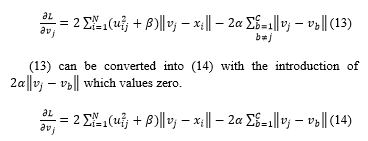1. Introduction

Clustering, one of the representative unsupervised learning methods, is a method for partitioning data into groups of similar objects and is one of the major techniques in pattern recognition. Since Zadeh [1] proposed the fuzzy set that represents the idea of partial membership described by a membership function, fuzzy clustering has been widely studied and applied in various areas [2]. Clustering combined with deep learning also has attracted much attention in recent years [3].

 In clustering, Fuzzy C-Means (FCM), generalized by Bezdek [4], is one of the most well-known methods. Although FCM is a simple and effective method, one of the shortcomings is that low-density cluster center moves towards high-density clusters because of the sum of Euclidean distances used in FCM. In real world data, it is more common that the data consist of clusters having different densities. Preventing the cluster distortion due to density difference is, therefore, one of the main problems to be solved in clustering especially in real world applications.

If the centers of some clusters are distorted, test data may belong to wrong clusters, which affects, in particular, the data points placed near the cluster boundary, and may cause a decrease in overall performance even with a small number of mis-clustered points.

There have been several variants of FCM that use cluster density, but most of the methods introduce an additional step to estimate cluster density and density estimation is performed independently from clustering, which has a disadvantage of additional computation [5, 6]. Even worse the estimation itself cannot be accurate as real world data do not follow any known distribution in general.

In this paper, a new clustering method that can solve the bias of cluster centers due to density difference is proposed. The proposed method has little increase in computational complexity and density estimation proceeds simultaneously with clustering. The proposed clustering method adds two terms to the objective function of FCM to reduce the sensitivity to cluster density. The first term represents the sum of distances between two cluster centers. This reduces the phenomenon that a low-density cluster center is attracted to a high-density cluster center by keeping cluster centers as far away as possible. However, if the centers are simply scattered and placed on the feature space boundary, the first term may have a small value. Therefore, the second term that represents the sum of the distances between data points and cluster centers is added so that cluster centers are located in high density regions.

Clustering error decreases with a large value in the first term, while it decreases with a small value in the second term. Experimental results show that FCM-CDI (FCM with Cluster Density Immunity), the enhanced FCM with two additional terms, is more likely to converge to real cluster center than FCM does.

In the next section, fuzzy clustering, especially FCM is summarized. Section 3 is devoted to develop an enhanced new clustering method through the introduction of new terms in the objective function of FCM. Experimental results are given in Section 4 and discussion in Section 5.

2. Fuzzy C-Means

Clustering is a method to make data belong to a specific cluster based on the concept of similarity. Fuzzy clustering is a way to extend this further, introducing the concept of incomplete membership in fuzzy so that data can be partly belonged to more than one clusters. Various methods for clustering has been proposed for a long time and one of the representative methods is FCM proposed by Bezdek [4]. FCM can be represented as a constrained optimization problem [7, 8]. Given N d-dimensional data points , the objective function of (1) should be minimized to divide data points into C clusters.

where u_ij is the membership of the ith data point x_i to the jth cluster, v_j is the center of the jth cluster, m is a fuzzifier constant, usually 2 (1 < m). d_ij is the distance between the ith data point x_i and the center of the jth cluster v_j. In this paper, Euclidean distance is used to calculate the distance between a data point and a cluster center.

One data point x_i can be belonged to more than one cluster in FCM. However, the degree of belonging to each cluster, that is, the membership is different from each other, and the degree of belonging to C clusters should satisfy the constraint that the sum of total membership should be one, often called sum-to-one constraint.

The membership values and cluster centers that minimize the objective function of (1) while satisfying the constraint of (2) can be obtained by iterative optimization method using the update equations in (3) and (4) derived from a Lagrange equation.

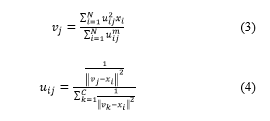FCM has been successfully used for many problems in its original or modified form for a given problem since it was firstly introduced, but the existence of numerous variants is a proof that FCM is not good for all problems. This paper also proposes a modified FCM to solve the problem of finding wrong cluster centers when FCM is applied to the data composed of clusters with different densities.

3. FCM with Cluster Density Immunity

In the presence of clusters with different densities in FCM, some cluster centers moves toward a high density cluster because FCM is based on the sum of Euclidean distances (or variations) between cluster centers and data points [9, 10]. That is, each data point  has the same effect on FCM objective function. There are methods of assigning different weight to each data point according to its density, but estimating densities of all data points require a lot of computation and it is not possible to estimate the density accurately. Therefore, in this paper, two terms are added to the objective function of FCM so that the density can be effectively reflected with small increase in computation compared to FCM.

The first one is the term that makes the distance between two cluster centers as far away as possible. The objective function of adding the sum of distances between two cluster centers is shown in (5) [11].

where α (> 0) is a constant indicating the rate at which the center sparsity is included in the objective function. The second term in (5) is the sum of the distances between two cluster centers. The larger the distance is, the smaller the objective value becomes. The cluster centers obtained by optimizing the objective function J₁ are located as far away as possible, but there can be one problem. As the value of α increases, cluster centers may move away from the actual cluster centers, and in the extreme case, cluster centers may be located in data-independent regions.

In order to reduce the side effect of the second term in (5), there is a need for a method defines candidate regions where cluster centers can come in addition to making cluster centers far away. In this paper, it is assumed that the candidate regions’ densities are high. However, as mentioned before, the computational complexity is high and the accuracy is low in direct density estimation, sum of distances between a data point and a cluster center is used to estimate the density indirectly. As cluster center moves to a high density region, the sum of distances between a cluster center and a data point becomes small. The new objective function where the sum of distances between a cluster center and a data point is added to the objective function of FCM can be written as (6) [12].

where β (> 0) represents the ratio of reflecting the degree to which cluster centers are located in high density regions to the objective function. The second term, added to the objective function of FCM, is the sum of distances between a cluster center and a data point. The smaller the distance is, the smaller the objective function becomes. The cluster centers obtained by optimizing the objective function J₂ are located in high density regions, but there is one problem. In the extreme case, if all the cluster centers are located at one position with the highest density, (6) can be minimized.

As explained above, it is difficult to effectively remove the influence of cluster density difference by using only one of the two proposed terms. Therefore, this paper proposes FCM-CDI (FCM with Cluster Density Immunity) using two terms together. The objective function of FCM-CDI is shown in (7), which allows cluster centers to be located in high density regions while keeping cluster centers as far away as possible.

Using (10) and (11), one can obtain (12), which is the update equation for u_ij in FCM-CDI.

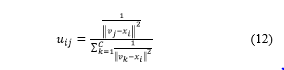The update equation in (12) is the same as the one in FCM. In FCM-CDI, the membership is determined based on the Euclidean distance between a cluster center and a data point, as in FCM.

The Lagrange equation can be partially differentiated with respect to v_j to obtain the update equation for a cluster center.

 (14) is more simple to use than (13) as a condition  is removed. One can obtain (15) by equating (14) to zero and solving it for v_j.

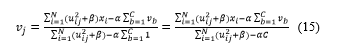When compared (15) with (3), cluster center update equation in FCM, it can be seen that the two new terms are applied in denominator and numerator respectively. The update equation obtained when β = 0 in (15) corresponds to the update equation for the objective function J₁ in (5). In addition, the update equation obtained when α = 0 in (15) corresponds to the update equation for the objective function J₂ in (6). That is, the objective functions in (5) and (6) correspond to special cases of FCM-CDI.

FCM-CDI can be expressed as shown in Figure 1 using the update equations in (12) and (15). The convergence condition in Figure 1 is that the maximum difference of two center positions between two successive iterations is smaller than or equal to  and the maximum difference of two membership values between two successive iterations is smaller than .

Figure 1: FCM-CDI Algorithm

4. Experimental Results

Although there are various FCM variants, there is no way to reduce the clustering error due to density difference through the modification of FCM itself. Therefore, in this paper, FCM and FCM-CDI are compared, and three different objective functions in (5), (6) and (7) are used to demonstrate the effect of each term on clustering result.

Figure 2 shows the typical results of FCM and FCM-CDI. The data were randomly generated with Gaussian distributions with the centers provided in advance. The cluster on the upper right has 500 data points and the other 2 clusters have 100 data points to make density difference.

As shown in Figure 2-(a), the cluster center is shifted toward a high density cluster in FCM, but the cluster center is approaching to the actual cluster center in FCM-CDI. Since clustering is an unsupervised learning method, it is difficult to quantitatively compare the results. Therefore, in this paper, an error function is defined as the sum of distances between the actual cluster center used for data generation  and the cluster center obtained through clustering  as in (15).

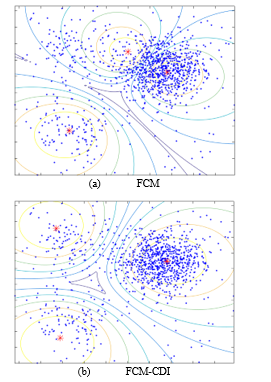Figure 2: Clustering results with data having 3 clusters

The objective function in (7) requires two constants α and β to be determined. In order to determine these constants, ① the α value with the smallest average error was experimentally determined with the objective function J₁ in (5) first. After that ② the β value with the smallest average error was experimentally determined with the objective function J_FCM-CDI. In the second step, the α value was fixed to the value obtained in the first step. ③ When J₂ is used as the objective function, the value obtained in the second step is used as the β value.

Figure 3 shows the average error obtained by varying α value for the data in Figure 2. The values shown in Figure 3 are obtained by averaging 50 experimental results with the same value of α.

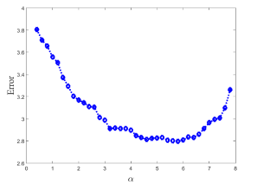Figure 3: Clustering error with respect to α on the data having 3 clusters

As shown in Figure 3, the error decreases as the value of α increases. However, if the value of α becomes larger than some value, the cluster centers pushed to the place where no real cluster centers as well as data points exist and the error increases. The α value with the smallest error for the data in Figure 2 was 5.8.

Figure 4 shows the average error obtained by varying the β value. The values shown in Figure 4 are also averages over 50 experiments.

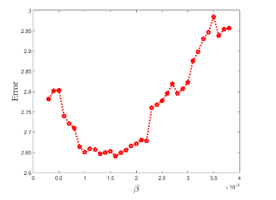Figure 4: Clustering error with respect to  on the data having 3 clusters

Figure 4 also looks similar to Figure 3. As the β value increases, the error decreases, but when the β value becomes larger, the cluster center shifts to the higher density region. Although the candidate region where the cluster center can be located is a high density one, high density only is not enough to be a candidate for center. The β value with the smallest error for the data in Figure 2 was 0.0016.

Table 1 summarizes the results of applying four objective functions to the data in Figure 2. The average error is the error averaged over 500 experiments using randomly generated data. For α and β, the values obtained in the previous experiments were used.

Table 1: Clustering results with data having 3 clusters

Method	Objective Function	Average Error
FCM	JFCM	3.3142
FCM-CDI	J1	2.8012
	J2	3.4021
	JFCM-CDI	2.6934

In FCM-CDI, the first term to make the cluster centers far away and the second term to place the cluster center in a high density region are introduced. As can be seen from Table 1, FCM-CDI showed better results than FCM in data consisting of clusters with large difference in density. However, FCM-CDI showed a larger error than FCM when only the second term (α = 0) was used. This is because cluster centers were randomly initialized [14, 15]. When one randomly initialized cluster center is close to another, the two cluster centers tends to move to the same position due to the second term. Therefore, a larger average error was obtained when only the second term was used. However, when both terms were used, the best results were obtained among the four methods. In addition, as the comparison with respect to initialization methods is completely different from the topic covered in this paper, only random initialization is considered.

Figure 5 shows clustering results applying FCM and FCM-CDI to the data composed of four clusters. In the data, the upper right cluster has 400 data points and the remaining 3 clusters have 100 data points.

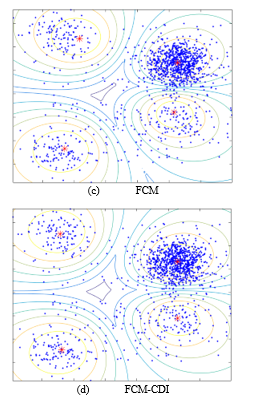Figure 5: Clustering results with data having 4 clusters

Table 2 summarizes the results of applying four objective functions to the data having four clusters as in Figure 5. As before, the average error is the error averaged over 500 experiments using randomly generated data.

When there are four clusters, the randomly initialized cluster centers are more likely to be close to each other. Therefore, compared to FCM, the result with the second term only was much worse than that of the previous one.

Table 2: Clustering results with data having 4 clusters

Method	Objective Function	Average Error
FCM	JFCM	1.5130
FCM-CDI	J1	1.3012
	J2	1.7218
	JFCM-CDI	1.1026

5. Conclusion

In this paper, proposed is a new clustering method to reduce the deviation of a cluster center from the actual center due to the density difference. The proposed clustering method is based on the fact that the centers should be as far away as possible and that the cluster center should be located in a high density region. Two new terms reflecting these considerations are added to the objective function of FCM, which results in more convergence to real centers.

It is true that the proposed method is robust against cluster density compared to FCM, but the existence of two constants α and β can be an obstacle to its application. Since the ground truth is known in this paper, the optimal value was found experimentally. However, since clustering is a kind of unsupervised learning, it is difficult to evaluate the performance by clustering itself and it should be indirectly evaluated by the performance of the whole system. Therefore, a method that can determine the optimal α and β according to the data given is needed and this is under study. In addition, cluster center initialization affects the performance as shown in the result, initialization method for the proposed method should be examined carefully, which is left as a future study.

1.  L. A. Zadeh, “Fuzzy sets,” Information and Control, 8(3), 338-353, 1965. https://doi.org/10.1016/S0019-9958(65)90241-X
2.  D. Xu and Y. Tian, “A Comprehensive Survey of Clustering Algorithms,” Annals of Data Science, 2(2), 165-193, 2015. https://doi.org/ 10.1007/s40745-015-0040-1
3.  E. Min, X. Guo, Q. Liu, G. Zhang, J. Cui, and J. Long, “A Survey of Clustering With Deep Learning: From the Perspective of Network Architecture,” IEEE Access, 6, 39501-39514, 2018. https://ieeexplore.ieee.org/document/8412085
4.  J. C. Bezdek, Pattern Recognition with fuzzy Objective Function Algorithms, Springer, 2013.
5.  C. H. Cheng, J. W. Wang, M. C. Wu, “OWA-weighted based clustering method for classification problem,” Expert Systems with Applications, 36(3), 4988-4995, 2009. https://doi.org/10.1016/j.eswa.2008.06.013
6.  C. Lu, S. Xiao, X. Gu, “Improving fuzzy C-means clustering algorithm based on a density-induced distance measure,” The Journal of Engineering, 2014(4), 137-139, 2014. https://doi.org/10.1049/joe.2014.0053
7.  S. Muyamoto, Handbook of Computational Intelligence, Springer, 2015.
8. J. Nayak, B. Naik, H. S. Behera, “Fuzzy C-means(FCM) Clustering Algorithm: A Decade Review from 2000 to 2014,” Computational Intelligence in Data Mining, 2, 133-149, 2015. https://doi.org/10.1007/978-81-322-2208-8_14
9. Z. Zainuddin, O. Pauline, “An effective Fuzzy C-Means algorithm based on symmetry similarity approach,” Applied Soft Computing, 35(C), 433-448, 2015. https://doi.org/10.1016/j.asoc.2015.06.021
10.  B. Abu-Jamous, R. Fa, A. K. Nandi, Integrative Cluster Analysis in Bioinformatics, Wiley, 2015.
11.  B. H. You, W. W. Kim, G. Heo, “An Improved Clustering Method with Cluster Density Independence,” Journal of The Korea Society of Computer and Information, 20(12), 15-20, 2015. https://doi.org/10.9708/jksci.2015.20.12.015
12.  S. H. Kim, G. Heo, “Improvement on Density-Independent Clustering Method,” Journal of the Korea Institute of Information and Communication Engineering, 21(5), 967-973, 2017. https://doi.org/10.6109/jkiice.2017.21.5.967
13.  I. M. Gelfand, S. V. Fomin, Calculus of Variations, Dover Publications, 2000.
14.  K. Zou, Z. Wang, M. Hu, “An new initialization method for fuzzy c-means algorithm,” Fuzzy Optimization and Decision Making, 7(4), 409-416, 2008. https://doi.org/10.1007/s10700-008-9048-8
15.  A. Stetco, X. J. Zeng, J. Keane, “Fuzzy C-means++: Fuzzy C-means with effective seeding initialization,” Expert Systems with Applications, 42(21), 7541-7548, 2015. https://doi.org/10.1016/j.eswa.2015.05.014

(Click Here)

(Click Here)