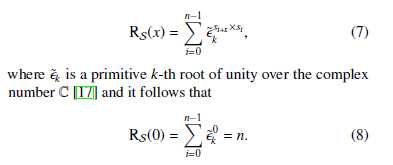1. Introduction

Pseudo random sequences of having random numbers are crucial components of many cryptographic applications, for instance, key generation, session keys, masking protocol, navigation, radar ranging, and so on [1, 2, 3]. The security of these cryptographic systems deliberately depends on the randomness and unpredictability regarding the sequence. By using the non-linearity features of some mathematical functions, a pseudo random sequence of having excellent randomness characteristics can be generated. The major substances for randomness are independency of values (or lack of correlation), unpredictability (or lack of predictability), and uniform distribution (or lack of bias) [4]. Therefore, a prominent pseudo random number generator is essential to generate pseudo random sequence having good randomness property.

Most renowned pseudo random number generators are the Mersenne Twister (MT) [5], Blum-Blum-Shub (BBS) [6], Legendre sequence [7], and M-sequence [8]. Among those, the former two pseudo random number generators (MT and BBS) are well known considering their applications in cryptography rather than the theoretical aspect. On the other hand, the M-sequence and Legendre sequence are prominent geometric sequences regarding the theoretical aspect. As a result, the authors attracted in the pseudo random sequence generation research area by observing the theoretical prospect on the M-sequence and Legendre sequences.

A well balanced pseudo random signed binary sequence proposed in our previous work [9]. It is generated by utilizing a primitive polynomial, trace function, and Legendre symbol. The period and autocorrelation properties of the well balanced signed binary sequence were explained based on some experimental results. This work is actually an extension of previous works on the signed binary sequence by introducing additional two parameters k and non-zero scalar A (where k and A are responsible for generating multi-value sequence and extending the sequence period to its maximum value, respectively). It should be noted that the k-th power residue symbol is actually an extension of the Legendre symbol, therefore, this power residue symbol includes the case of the well balanced signed binary sequence. Furthermore, this work is also an extension of our previous work on multivalue sequence [10] by considering additional two properties (linear complexity and distribution of bit patterns) and introducing its flexibility by making it binary sequence, whereas, previous multi-value sequence introduced along with its autocorrelation and cross-correlation properties (based on experimental observations only).

In this paper, the authors propose a well balanced multivalue sequence (including a binary sequence). Let f(x) be a primitive polynomial of degree m and ω ∈ F_q be its zero. Then, the sequence

S = {s_i} | s_i = Trωⁱ,i = 0,1,2,…,q − 2,…

becomes a maximum length sequence whose period is q − 2. Here, Tr(·) is a trace function which maps an element of the extension field F_q to an element of the prime field F_p. In brief, the proposed well balanced multi-value sequence generation procedure is as follows: in the beginning, a primitive polynomial generates maximum length sequence of vectors, then the Tr(·) maps vectors to scalars, next a non-zero prime field scalar A ∈ {1,2,…, p − 1} added to the scalars, and finally k-th power residue symbol maps the scalars to a well balanced multi-value (k + 1 values) sequence.

From the viewpoint of auto and cross-correlation, there are a lot of considerations to use multi-value sequence in communications [11, 12]. However, there are few papers regarding the usage of pseudo random binary sequence with a long period, high linear complexity, and good distribution of bit patterns in security applications. To make attention to the usability of the proposed sequence, the authors introduce the flexibility of their proposed well balanced multi-value sequence to make it more worthy. To do so, the authors explain how to transform their proposed sequence into a binary sequence (along with its linear complexity and distribution of bit patterns properties) due to the extensive usage of binary sequence in numerous applications (especially in cryptography).

All our previous works on sequence generation (both binary and multi-value) utilizes a mapping function during the sequence generation procedure. As a result, there exists a big difference between the appearance of sequence coefficients, which leads the distribution of bit patterns ununiform. On the other hand, the proposed sequence is a k + 1 values well balanced multi-value sequence without applying any kind of mapping function. Therefore, all the sequence coefficients (except the 0) appear almost the same in number, thus, it is called a well balanced multi-value sequence. This balanced characteristic in the sequence coefficients contributes to low correlation (both autocorrelation and cross-correlation), high linear complexity, and almost uniform distribution of bit patterns, whereas, a suitable pseudo random sequence for cryptographic applications asks for such kinds of features.

This paper experimentally explains some prominent features regarding a sequence, for instance, its period, autocorrelation, and cross-correlation. The authors formulate theorems by which the value of the autocorrelation and crosscorrelation can be explicitly given. This is one of the major contributions of this paper. Furthermore, to emphasize the usability of the proposed sequence, the authors introduce its flexibility by making it a binary sequence. In addition, a comparison result regarding the linear complexity and distribution of bit patterns properties are also included in this paper. According to the comparison results, the proposed sequence in this paper holds better properties compared to our previous sequence.

Notations

In this paper, the notation p denotes an odd characteristic prime, m be a extension degree, and q denotes the power of p, for instance, q = p^m. In addition, k is a prime number as

well as a factors of p − 1, such as k | stands for multiplicative group of F_q excluding the zero.

2. Preliminaries

This section briefly introduces a few mathematical fundamentals which are related to this research work such as primitive polynomial, trace function, and k-th power residue symbol. In addition, the multi-value sequence also introduced along with its properties.

2.1. Primitive Polynomial

A polynomial f(x) of degree m over the prime field F_p is said to be irreducible if it cannot be factorized into smaller degree polynomials (including the scalar factor), then f(x) is said to be an irreducible polynomial. Let e be an smallest positive integer and f(x) | (x^e − 1). If x = p^m − 1, then the polynomial f(x) is said to be a primitive polynomial.

Let ω be an arbitrary element in the extension field F_q. If f(ω) = 0, then ω is said to be the root of the primitive polynomial. In addition, ω becomes a primitive element in F_q and all the non-zero elements can be generated by the power of ωⁱ such as

ω⁰,ω¹,ω²,…,ω^q−2.

The primitive element ω has a multiplicative order of q − 1.

An extension field F_q and its base field F_p holds the following property [13].

Property 1 Let ω be a generator of F becomes a non-zero element in prime field F_p and is also a generator of F^∗_p.

2.2. Trace Function

A trace function is defined to find the sum of conjugates.

Let F_q be an extension field and X be one of the elements

(vector) of F_q. On the other hand, let x be a prime field F_p element (scalar). The trace of X over F_q is the sum of conjugates of X with respect to F_q. It is defined as follows:

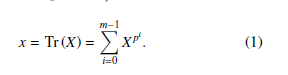Aforementioned the trace function Tr(·) sums the conjugates in the extension field F_q and maps them as the prime field F_p elements. As a result, it has a linearity property, which shown in the following equation.

where α,β are prime field F_p elements and X,Y are extension field F_q elements.

Property 2 Let i = 0,1,2,…, p − 1 ∈ F_p. Then for each i the number of elements in the extension field F_q whose trace with regard to the prime field F_p becomes i be given by q/p = p^m−1.

2.3. k-th Power Residue Symbol

The k-th power residue symbol with (k > 2) is a generalization of the Legendre symbol to k-th powers [14]. Let a be an arbitrary element in the prime field F_p, then the k-th power residue symbol a/_p can be defined as follows [15]:

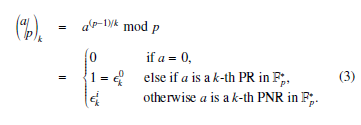Throughout this paper, k is a prime number as well as a factor of p − 1, such as k | (p − 1). According to the definition of the k-th power residue symbol a/_p , a is called as the k-th

Power Residue, when it has a k-th root in the base field F_p. On the other hand, a is called as k-th Power Non-Residue. In addition, here _k is a primitive k-th root of unity belongs to F_p and it holds the relation 0 ≤ i < k.

In Eq. (3), the value of the exponent i will be within the range of 0 ∼ k − 1, since _k^k = _k⁰ = 1. The k-th power residue symbol translates the scalars generated by the trace function Tr(·) to a multi-value sequence. Thus, the sequence coefficients will be {0,_kⁱ}, where i ∈ {0,…,k − 1}. In this paper, an alternate representation of the exponent i in Eq. (3) is as follows: i =

Furthermore, the k-th power residue symbol holds the following property.

Property 3 For each i from 0 to k − 1, the number of nonzero elements in F_p such that

2.4. Multi-value Sequence and Its Properties

In this section, the proposed multi-value sequence introduced along with its period, autocorrelation, cross-correlation, linear complexity and distribution of bit patterns properties.

2.4.1       Notation

Throughout this paper, the proposed multi-value (more specifically, k + 1 values) sequence S will be denoted as follows:

where n denotes the period of the proposed sequence S. In addition, here s_i = s_n+i.

2.4.2       Autocorrelation and Cross-correlation

The autocorrelation of a sequence is a measure for how much a sequence differs from its each shift value. In addition, the period and other patterns regarding a sequence can be obtained by evaluating the autocorrelation property [16]. Let S = {s_i} be a sequence and x be the shift value, then the autocorrelation R_S(x) of S can be calculated by using the following equation as,

Furthermore, the cross-correlation property is as important as the autocorrelation property. It defines the similarities between two completely different sequences. If multiple sequences are used in an application (more specifically in any security application), then it is important to analyze their cross-correlation property to evaluate how much similar these sequences to each other. Considering this point, the cross-correlation value is preferred to be low [18, 19]. Let ^Sˆ = {sˆ_i} and S = {s_i} be two sequences and x be the shift value, then the cross-correlation R_S(x) between ^Sˆ and S can be calculated by using the following equation as,

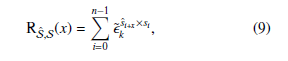where ˜_k is a primitive k-th root of unity over the complex number C [20, 21].

2.4.3       Linear Complexity

The linear complexity regarding a sequence is a measure of unpredictability by the length of the shortest Linear Feedback Shift Register (LFSR). In the literature, this length of the LFSR is referred to as the linear complexity [22]. The Berlekamp-Massey algorithm is an efficient method of determining the linear complexity of a sequence [23]. The forward unpredictability can be confirmed by the linear complexity property.

To calculate the linear complexity of a sequence S = {s₀, s₁,…, s_n−1}, at first, the sequence S needed to be represented by the polynomial expression S(x) as follows:

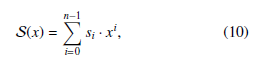where n denotes the period of the sequence S. If we consider a binary sequence, then the sequence coefficients s_i ∈ {0,1}, in other words, s_i belongs to F₂. On the other hand, in case of multi-value sequence (k-values sequence), s_i ∈ {0,1,2,…,k − 1}, furthermore, s_i ∈ F_k. After translating the sequence into polynomial, the linear complexity is evaluated by utilizing the equation in below (over F₂ or F_k).

In the above equation, deg(f(x)) denotes the degree of the primitive polynomial f(x).

2.4.4       Distribution of Bit Patterns

The distribution of bit patterns is an important measure to judge the randomness of a sequence. As a reference, an M-sequence is well known for its uniform distribution of bit patterns. A uniform distribution of bit patterns means all the bit patterns (1-bit pattern, 2-bit patterns, 3-bit patterns, and so on) appear the same in number. Assume an M-sequence of having a period of 15 as follows and its bit distribution is shown in Table 1.

S₁₅ = {1,0,0,0,1,1,1,1,0,1,0,1,1,0,0}.

Table 1: Uniform distribution of bit distribution of an M-sequence ^[1].

n	Hw b(n)	Z b(n)	DS15 b(n)
1	0	1	7
	1	0	8
2	0	2	3
	1	1	4
	2	0	4
3	0	3	1
	1	2	2
	2	1	2
	3	0	2

In an M-sequence, except 0 all the bit patterns appear same in number, therefore, the distribution of bit patterns of M-sequence is known as uniform.

It should be noted that the randomness and bit patterns hold a strong relationship with each other. In other words, the more uniform distribution of bits in a sequence, the sequence is more random.

3. Proposed Multi-value Sequence

The authors propose a well balanced multi-value sequence S by combining the features of the trace function and k-th power residue symbol. Assume that in the extension field F_q, ω be a primitive element. Furthermore, A is a non-zero scalar which belongs to the prime field F_p. Then, the proposed sequence S is defined as follows:

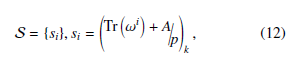here k is a factor of p−1, such as k | (p−1). The sequence coefficients s_i in Eq. (12) can be described as the exponent of _k, such as _k^e. For instance, let p = 7 and k = 3, then the sequence coefficients in this example becomes s_i ∈ {0,1,2,4} and the 3-rd primitive root in F₇ is equal to 2 or 4. In addition, let us fix 2 as a 3-rd primitive root. Then all of the non-zero sequence coefficients can be represented as an exponent of primitive root 2, this relation is developed as,

₃{1,2,4} = {2⁰,2¹,2²} = {₃⁰,₃¹,₃²}.

At first, the authors will focus on the autocorrelation and cross-correlation properties regarding the proposed sequence. It should be noted that the autocorrelation and cross-correlation are very close to each other. The main difference between them is the cross-correlation is calculated between two different sequences and the autocorrelation is focused in a single sequence. Thus, in the beginning, let us focus on the cross-correlation property. As mentioned earlier, using two different sequences of having the same period the cross-correlation is calculated. Let, S and S^ˆ be two different sequences which are defined as follows:

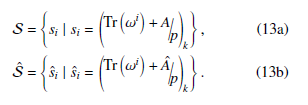Here, A and Aˆ are non-zero elements in F_p can be represented by a generator g ∈ F_p such as

here h satisfies the relation 0 ≤ h ≤ p − 2 and g needs to be given by ω^{(pm−1)/(p−1)}. When the value of h = 0, that is Aˆ = A which means ^Sˆ and S becomes the same sequence.

Thus, the cross-correlation becomes the autocorrelation of S. After inspecting several experimental results, it was found that the value of the cross-correlation explicitly given by the following theorem.

Theorem 1 The cross-correlation between the two sequences S^ˆ and S is defined by the Eq. (13) is as follows:

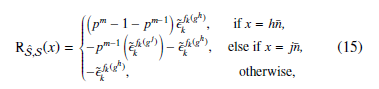If the value of h = 0, then S^ˆ = S which actually means they becomes the same sequence. In this case, the crosscorrelation in Eq. (15) becomes the autocorrelation after replacing the value h = 0.

Theorem 2 The autocorrelation of a sequence S is given as follows:

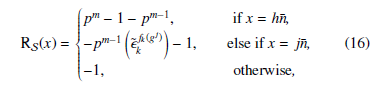Corresponding to the above autocorrelation equation, the period of the proposed well balanced multi-value sequence undeniably given by p^m − 1.

In the next section, the authors will introduce experimental observation regarding the period, autocorrelation and cross-correlation properties.

4. Example and Discussion

This section experimentally observes the proposed multivalue sequence properties such as its period, autocorrelation, and cross-correlation along with some examples. In this section, the notation S₂ denotes the proposed sequence with the parameter A = 2. The proposed sequence in this paper is a multi-value sequence, thus its correlation is calculated over the complex number C. To represent the absolute value of a complex number x, this section uses the notation |x|.

4.1.  p=7,m=2,k=3, and A=2,3

Assume, x²+4x+5 be a primitive polynomial over F₇. Then, the generated sequence S₂ having a period of 48 (p^m − 1 = 7² − 1 = 48) is shown as follows:

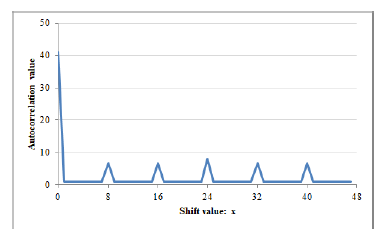Figure 1: |R_S2(x)| with p = 7,m = 2,k = 3, and A = 2.

To confirm the well balanced property in the proposed multi-value sequence, the authors introduce sequence coefficients appearance in the following Table 2. According to the table, it was found that in every case all of the sequence coefficients (except the 0) appears almost the same in number. This is one of the positive properties of the proposed sequence, thus, it is called as a well balanced sequence.

Table 2: Appearance of the sequence coefficients.

sequence coefficient	number of appearance
0	7
1	14
2	14
4	13

On the other hand, S₃ is given as follows. It should be noted that the sequence S₃ is different from the sequence S₂, but both of them having the same period.

The autocorrelation of this generated sequence S₃ is calculated by the Eq. (7) and autocorrelation graph of S₂ is shown

The cross-correlation of S₂ and S₃ becomes as follows and the cross-correlation graph shows in Figure 3.

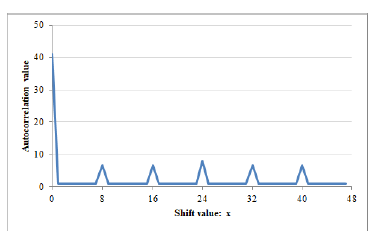Figure 2: |R_S3(x)| with p = 7,m = 2,k = 3, and A = 3.

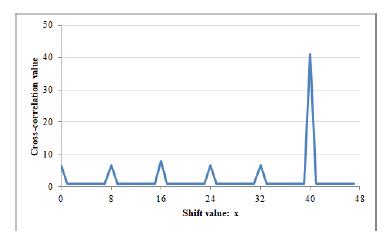Figure 3: |R_S2,_S3(x)| with p = 7,m = 2, and A = 2,3.

4.2.  p=13,m=3,k=3, and A=6,7

Assume, x³+6x²+3x+7 be a primitive polynomial over F₁₃. Then, the period of this generated sequence becomes 2196. Here, Figure 4 and Figure 5 respectively represents the autocorrelation graph of S₆ and S₇. Their cross-correlation graph is shown in Figure 6.

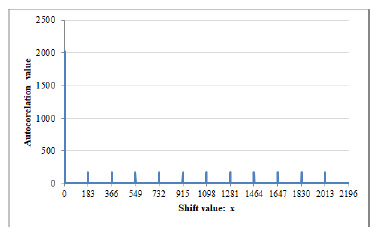Figure 4: |R_S6(x)| withp = 13,m = 3,k = 3,and A = 6.

After observing the cross-correlation graphs, it was found that in each graph the number of peaks exactly is given by p − 1. Only a single peak has the maximum value, as an example, in Figure 3 the maximum peak value is 41 that corresponds to the first case (x = hn¯) of Eq. (15). Remaining p − 2 smaller peaks conforms to the second case (x = jn¯). Except all of these peak values, the remaining parts of the cross-correlation graph consistently having a constant value of 1, which confirms the final case of Eq. (15). It should be noted that only changing the value of non-zero scalar parameter A ∈ F_p, different sequences can be generated. It is also observed that by changing all the other parameters such as primitive polynomial f(x), extension degree m, non-zero scalar A, and prime factor k does not have any impact in the correlation (both autocorrelation and cross-correlation) evaluation.

Alike the cross-correlation, autocorrelation also have a p−1 number of peaks. Among them, only one peak hold the maximum value, while other peaks have small values and remaining parts holds a constant value of 1 and all of these values explicitly given by the Eq. (16).

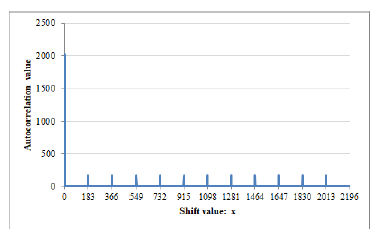Figure 5: |R_S7(x)| withp = 13,m = 3,k = 3,and A = 7.

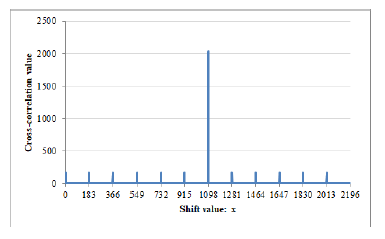Figure 6: |R_S6,_S7(x)| with p = 13,m = 3, and A = 6,7.

5. Flexibility of the Proposed Sequence and Its Application

Although nowadays multi-value sequence does not have enough application except the binary sequence especially in security applications. Therefore, the authors emphasize the flexibility of their proposed sequence to make it more worthy. To do so, the authors in this section, explains how to transform their proposed sequence into a binary sequence. In addition, this section also describes a comparison with our previous work [24] in terms of the linear complexity and distribution of bit patterns like crucial properties from the experimental viewpoint.

5.1. Proposed Binary Sequence

Binary sequences are extensively used in numerous applications (especially in cryptography). Although the authors proposed sequence is a multi-value sequence, it can be easily mapped into a binary sequence by setting the parameter value k = 2 and using the mapping function M₂(·). As mentioned previously, the proposed multi-value sequence is a well balanced sequence, in other words, all of the sequence coefficients (except the 0) appears same in number. To maintain the same property, the authors utilized the following algorithm (Algorithm 1) to make a uniform binary sequence from the well balanced multi-value sequence.

To make it binary sequence, a mapping function (introduced in the following algorithm) is defined as,

Algorithm 1 Generating procedure of the proposed uniform binary sequence

1: generate primitive element ω ∈ F_pm

2: initialize flag f ← 0

3: for i = 0 to p^m − 2 do

4:         compute ωⁱ

5:              a ← Trωi + A/p

6:           if a = 0 and f = 0 then

7:               a ← 1, f ← 1

8:         else

9:                a ← p − 1, f ← 0

10:        end if

11:         s_i = M₂ (a)

12: end for

After using the above algorithm, the well balanced multivalue sequence in Eq. (20) can be transformed into a binary sequence as follows.

5.2. Comparison with Our Previous Work

Before applying any sequence in some security application, a lot of sequence properties needs to be well studied such as its period, autocorrelation, cross-correlation, linear complexity, distribution of bit patterns, and so on. The authors already discussed the former three properties. Additionally, this paper also includes a comparison with our previous work [24] regarding the linear complexity and distribution of bit patterns like crucial properties from the experimental viewpoint. It should be noted that from here on the authors previous sequence proposed in [24] will be called as NTU (Nogami-Tada-Uehara) sequence.

Linear Complexity

The linear complexity is an important measure to judge the unpredictability of a sequence. Thus, before recommending a sequence for any security application, its linear complexity needs to be well-studied. The linear complexity of the proposed sequence (binary case) and NTU sequence (previous sequence) having a period of 2400 are shown in Figure 7 and Figure 8, respectively. According to the comparison result, it is found that in both cases the linear complexity reaches to their maximum value. Since the M-sequence has the minimum linear complexity [25], on the other hand, the Legendre sequence has the maximum linear complexity [8]. It should be noted that the proposed sequence for being a well balanced sequence, its linear complexity reaches to its maximum value.

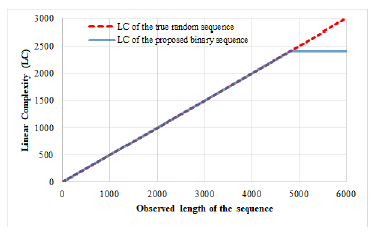Figure 7: Linear complexity of the proposed sequence (binary case).

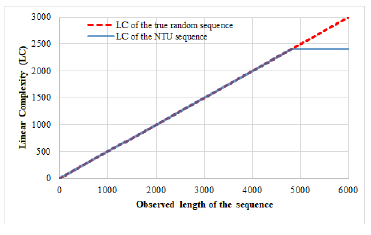Figure 8: Linear complexity of the NTU sequence.

Distribution of Bit Patterns

The randomness of a sequence can be evaluated by observing the distribution of bit patterns of it. The bit pattern of the proposed sequence (binary case) and NTU sequence (previous sequence) having a period of 117648 are shown in Table 3. In the following table, the notations n,b⁽ⁿ⁾,Z b⁽ⁿ⁾, and D_S b⁽ⁿ⁾ means length of a bit pattern, specific bit pattern, number of zeros in b⁽ⁿ⁾, and appearance of b⁽ⁿ⁾ in numbers in a sequence period, respectively. According to the comparison result, it is found that the distribution of bit pattern of the proposed binary sequence is almost uniform compared to NTU sequence.

The authors applied k = 2 and M₂(·) mapping function to make a uniform binary sequence from the well balanced multi-value sequence. It should be noted that after applying such a mapping function and uniformization algorithm, the sequence properties remains almost the same. For instance, only a small amount of change in the peak values regarding the autocorrelation, linear complexity remains the maximum, and distribution of bit patterns becomes almost uniform. In other words, they exhibit almost the same properties. It means the authors proposed sequence possesses a great flexibility.

Table 3: A comparison of distribution of 4-bit patterns between the proposed sequence (binary case) and NTU sequence.

n	b(n)	Z(b(n))	(proposed sequence) DS (b(n))	(NTU sequence) DS (b(n))
1	0	1	58824	67227
	1	0	58824	50421
2	00	2	28852	38415
	01	1	29972	28812
	10	1	29972	28812
	11	0	28852	21609
3	000	3	13927	21951
	001	2	14925	16464
	010	2	15066	16464
	011	1	14906	12348
	100	2	14925	16464
	101	1	15047	12348
	110	1	14906	12348
	111	0	13946	9261
4	0000	4	6680	12543
	0001	3	7247	9408
	0010	3	7391	9408
	0011	2	7534	7056
	0101	2	7402	7056
	0010	3	7664	9408
	0111	1	7631	5292
	0100	3	7275	9408
	1000	3	7247	9408
	1001	2	7678	7056
	1010	2	7675	7056
	1011	1	7372	5292
	1100	1	7523	5292
	1101	1	7383	5292
	1110	1	7275	5292
	1111	0	6671	3939

As far the authors know, there are a lot of considerations to use multi-value sequence in communications from the viewpoint of correlation [11, 12]; however there are few papers regarding the usage of pseudo random sequence with a long period, high linear complexity, and good distribution of bit patterns in security applications. The most typical security application of the pseudo random binary sequence will be the XOR-based stream cipher. First of all, in such an application, the same key is used for both encryption and decryption. Thus, each user should have a different key. In this case, these keys should have a minimum cross-correlation property compared to each other. Under this circumstance, it is important to discuss the cross-correlation property between several sequences along with linear complexity and distribution of bit patterns properties. The authors briefly introduced a use case in the following section of their proposed well balanced sequence in this paper, to emphasis on its usability.

5.3. Application

One of the most common applications of the pseudo random sequence (binary case) is in a stream cipher. Basically, a stream cipher is divided into two classes: block cipher and stream cipher. Among these a block cipher uses the same key for both encryption and decryption of each block (≤ 64 bits) of data. On the other hand, in case of a stream cipher, encryption and decryption are performed by the bit wise ⊕ (XOR) operation with a key stream. Here, the authors restrict the discussion of their proposed pseudo random binary sequence in a stream cipher. An image of the stream cipher is shown in Figure 9. Few important considerations during the design of a stream cipher are the key (which used for both encryption and decryption) should have a long period, good randomness, and unpredictability properties due to the usage of the same key in both encryption and decryption. Here, the encryption is carried out by applying a bit-wise ⊕ (XOR) operation between the plain-text of byte stream M and encryption key K. Then, the cipher-text C is transmitted through a network.

On the other hand, during the decryption, after the bit-wise ⊕ operation between the cipher-text C and the same key K, we will get the original plain-text M. In a stream cipher, a lot of sequences are assigned to several users, respectively. If these sequences have some correlation, then it will make some security vulnerabilities. Under this circumstance, it is important to observe the cross-correlation property between several sequences. Additionally, its linear complexity and distribution of bit patterns needs to be high and uniform, respectively to confirm its randomness. Although the authors proposed sequence is a well balanced sequence, it can be easily mapped into a binary sequence with a long period, typical auto and cross-correlation, high linear complexity, and almost uniformly distributed bit patterns features. After observing the experimental and comparison results, it can be concluded that the authors proposed well-balanced sequence (binary case) can be a prominent candidate for a stream cipher like applications.

6. Conclusion

The authors have proposed a multi-value sequence (including a binary sequence) which defined over the odd characteristic field. The k-th power residue symbol utilized in this paper which is an extension of the Legendre symbol. Additionally, the proposed sequence also includes the case of the signed binary sequence. Prominent features regarding a sequence for instance, its period, autocorrelation and cross-correlation of the proposed sequence discussed based on experimental results along with a theorem (by which the value of the correlation can be explicitly given). In addition, the authors also introduced the flexibility of their proposed sequence by making a binary sequence from a well balanced multi-value sequence. Furthermore, a comparison result regarding the linear complexity and distribution of bit patterns properties are also included in this paper. According to the comparison results, the authors proposed well balanced sequence holds better properties compared to our previous sequence.

As a future work, the more efficient calculation will be introduced for instance power residue symbol needs exponentiation calculation.

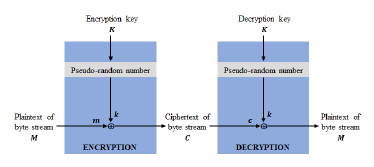Figure 9: Application of the proposed sequence (binary case) in stream cipher.

Conflict of Interest

The authors declare no conflict of interest. [1] The notations n,H_w b⁽ⁿ⁾ ,Z b⁽ⁿ⁾ , and, D_S b⁽ⁿ⁾ means length of a bit pattern b⁽ⁿ⁾, Hamming weight of the bit pattern b⁽ⁿ⁾, number of zeros in b⁽ⁿ⁾, and appearance of b⁽ⁿ⁾ in numbers in a sequence period, respectively.

1. M. Luby, Pseudorandomness and Cryptographic Applications, Princeton Univ. Press, 1996. https://doi.org/10.1016/0898-1221(96)87348-2
2.  T. W. Cusick, C. Ding, and A. Renvall, Stream Ciphers and Number Theory, North-Holland Math. Library, North-Holland Publishing Co.,Amsterdam, 1998. https://doi.org/10.1016/s0924-6509(98)x8001-3
3.  S. W. Golomb and G. Gong, Signal Design for Good Correlation: For Wireless Communication, Cryptography, and Radar, Cambridge University Press, NY, 2005. https://doi.org/10.1017/CBO9780511546907
4.  A. Kinga, F. Aline, and E. Christain, “Generation and testing of random numbers for cryptographic applications”, Proc. of the Romanian Academy, 13(4), pp.368–377, 2012.
5.  M. Matsumoto, and T. Nishimura, “Mersenne twister: A 623-dimensionally equidistributed uniform pseudo-random number generator”,ACM Transactions on Modeling and Computer Simulation, 8(1), pp.3–30, 1998. https://doi.org/10.1145/272991.272995
6.  L. Blum, M. Blum, and M. Shub, “A simple unpredictable pseudorandom number generator”, SIAM Journal on Computing, 15(2),
   pp.364–383, 1986. https://doi.org/10.1137/0215025
7.  J. S. No, H. K. Lee, H. Chung, H.Y. Song, and K. Yang, “Trace representation of Legendre sequences of mersenne prime period”, IEEE Transactions on Information Theory, 42, pp.2254–2255, 1996.https://doi.org/10.1109/18.556617
8.  C. Ding, T. Helleseth, and W. Shan, “On the linear complexity of Legendre sequences”, IEEE Transactions on Information Theory, 44,pp.1276–1278, 1998. https://doi.org/10.1109/18.669398
9.  A. M. Arshad, Y. Nogami, C. Ogawa, H. Ino, S. Uehara, and R. H.Morelos-Zaragoza, “A new approach for generating well balanced pseudo random signed binary sequence over odd characteristics field”,International Symposium on Information Theory and Its Applications (ISITA), Monterey, CA, USA, 2016. ISBN 978-4-88552-309-0.
10.  A. M. Arshad, Y. Nogami, H. Ino, and S. Uehara, “Auto and cross correlation of well balanced sequence over odd characteristic field”, Fourth International Symposium on Computing and Networking (CANDAR),Hiroshima, Japan, 2016. https://doi.org/10.1109/candar.2016.0109
11.  Y. K. Han and K. Yang, “New M-array sequence families with low correlation and large size”, IEEE Transactions on Information Theory, 55(4), pp.1815–1823, 2009. https://doi.org/10.1109/tit.2009.2013040
12.  N. Y. Yu and G. Gong, “Multiplicative characters, the weil bound, and poly phase sequence families with low correlation”, IEEE
    Transactions on Information Theory, 56(12), pp.6376–6387, 2010. https://doi.org/10.1109/tit.2010.2079590
13.  R. Lidl and H. Niederreiter, Finite Fields (Encyclopedia of Mathematics and Its Applications), Cambridge Univ. Press, 1996.
    https://doi.org/10.1017/CBO9780511525926
14.  E.R. Berlekamp, Algebraic Coding Theory, Aegean Park Press, Revised edition, 2014. https://doi.org/10.1142/9407
15.  M. Joye and B. Libert, “E_cient cryptosystems from 2k-th power residue symbols”, in Proceedings of Eurocrypto 2013, Johansson T. et al. Ed., ser. LNCS, vol. 7881. Berlin, Heidelberg: Springer, pp.76–92, 2013. https://doi.org/10.1007/978-3-642-38348-9 5
16.  P. V. Kumar and O. Moreno, “Prime-phase sequences with periodic correlation properties better than binary sequences”, IEEE
    Transactions on Information Theory, 37(3), pp.603–616, 1991. https://doi.org/10.1109/18.79916
17.  P. V. Kumar, T. Helleseth, A. R. Calderbank, and A. R. Hammons, “Large families of quaternary sequences with low correlation,” IEEE Transactions on Information Theory, 42(2), pp. 579–592, 1996.
    https://doi.org/10.1109/18.485726
18.  D. Hertel, “Cross-correlation properties of perfect binary sequence”, in Sequences and Their Applications SETA 2004, T. Helleseth et al. Ed., ser. LNCS, vol. 3486. Berlin, Heidelberg: Springer, pp.208–219, 2005. https://doi.org/10.1007/11423461 14
19.  D. V. Sarwate and M. B. Pursley, “Cross-correlation properties of pseudorandom and related sequences”, Proceedings of IEEE, 68(5), pp.593–619, 1980. https://doi.org/10.1109/proc.1980.11697
20.  Y. T. Kim, M. K. Song, D. S. Kim, and H. Y. Song, “Properties and cross-correlation of decimated sidelnikov sequences”, IEEE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, E97-A(12), pp.2562–2566, 2014.
    https://doi.org/10.1587/transfun.e97.a.2562
21.  G. Gong, “New designs for signal sets with low cross-correlation, balance property and large linear span: GF(p) case”, IEEE Transactions on Information Theory, 48(11), pp.2847–2867, 2002. https://doi.org/10.1109/tit.2002.804044
22. R. A. Rueppel, “Linear Complexity and Random Sequences”, F. Pichler (Ed.): Advances in Cryptology-EUROCRYPT’85, Springer, LNCS 219, pp. 167-188, 1986. https://doi.org/10.1007/3-540-39805-8 21
23.  A. Alecu and A. Salagean, “Modified Berlekamp-Massey Algorithm for Approximating the k-Error Linear Complexity of Binary Sequences”, IMA Conference on Cryptography and Coding (S.D.Galbraith, Ed.), Springer, LNCS, vol. 4887, pp. 220–232, 2007.
    https://doi.org/10.1007/978-3-540-77272-9 14
24.  Y. Nogami, S. Uehara, K. Tsuchiya, N. Begum, H. Ino, and R. H. Morelos-Zaragoza, “A Multi-value Sequence Generated by Power Residue Symbol and Trace Function over Odd Characteristic Field”, IEICE Trans. on Fund. of Electronics, Communications and Computer Sciences, E99.A(12), pp.2226–2237, 2016.
    https://doi.org/10.1587/transfun.e99.a.2226
25.  T. Moriuchi and S. Uehara, “Periodic sequence of the maximum linear complexity simply obtained from an m-sequence”, IEEE International Symposium on Information Theory (ISIT), 1991. https://doi.org/10.1109/isit.1991.695231

(Click Here)

(Click Here)