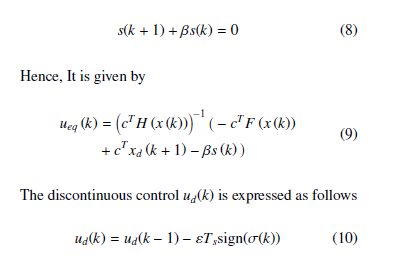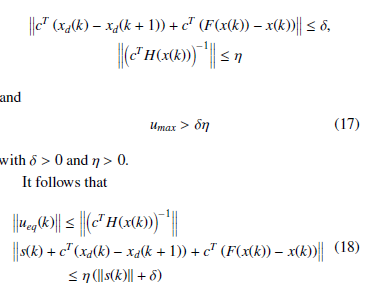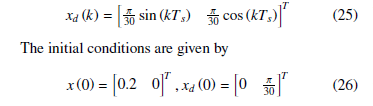1. Introduction

This paper is an extension of work originally presented in 2018 15th International Multi-Conference on Systems, Signals and Devices (SSD) [1]. Due to the increasing use of computers in control applications, discrete-time sliding mode control (DSMC) has been extensively developed since its appearance with Milosavljevic in 1985 [2]; see, for example, [3–9]. However, the finite sampling time negatively impacts the robustness of continuous-time sliding mode control to external disturbances, parametric uncertainties and modeling errors [10–12]. In fact, the control input remains constant during the sampling period so that it can not be changed when the trajectory of system state crosses the sliding surface. This is at the origin of chattering phenomenon that may badly affect control devices and system performances [13].

Introduced by Gao in 1995 [14], the quasi-sliding mode concept consists to drive the state trajectory to cross the sliding hyperplane in finite-time, to move with a non-increasing zigzag motion and to remain within a specified layer. Thus, the above-mentioned drawback can be reduced but not eliminated. Several approaches was proposed in the literature to overcome it. In [15–17], the saturation function is used as smooth one instead of the sign function which is the origin of discontinuity. In [18–20], discrete-time second order sliding mode control (DSOSMC) was proposed for linear and nonlinear systems. In [21, 22], a piecewise-constant control is used to generate the discrete-time sliding mode. It ensures that the chatter effect is avoided and the system state trajectory convergences to the sliding surface after a finite-time interval.

In the following, an optimal discrete-time sliding mode control (ODSMC) is proposed for single-input single-output (SISO) nonlinear systems with input constraints. Particle swarm optimization (PSO) algorithm is employed to search the sliding vector to which corresponds the optimal response characteristics of the closed-loop system and its behavior follows the reference model. Developed by Eberhart and Kennedy in 1995 [23], PSO algorithm is based on food searching behavior of animals societies having no leaders in their swarm such as bird flocks and fish schools. Its main advantages are the easiness of implementation, the robustness in controlling parameters and the good efficiency in solving nonlinear, nondifferentiable and large search space problems [24,25]. Regarding the control law, it is designed in such a way that chattering phenomenon is eliminated, the convergence to the sliding manifold is ensured in finitetime and the system dynamics are stable while respecting constraints.

The efficiency of the proposed controller will be demonstrated by applying it to an inverted pendulum system and by comparing it to DSMC controller using the saturation function and to DSOSMC controller with an arbitrary choice of control parameters and without taking into account the input constraints.

This paper is organized as follows. The DSMC and DSOSMC controllers are developed for SISO nonlinear systems in sections 2 and 3. Section 4 is devoted for the design of the proposed ODSMC controller. The inverted pendulum system is represented in section 5. Section 6 illustrates numerical simulation results. Concluding remarks are given in section 7.

2. Discrete-time Sliding Mode Control

Consider a class of discrete-time SISO nonlinear system described by

where x(k) ∈ IR^n×1 is the state vector, u(k) ∈ IR is the control input, and y(k) ∈ IR is the system output. F (x(k)) ∈ IR^n×1 and H (x(k)) ∈ IR^n×1 are vectors of nonlinear functions and C is the output matrix. Let’s admit that H and its pseudoinverse H⁺ are both bounded.

The sliding function is defined as follows

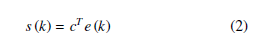where e(k) = x(k) − x_d (k) is the tracking error and c^T ∈ IR^1×n is the sliding vector chosen such that the sliding dynamic s(k) ≡ 0 is asymptotically stable. The reaching law is given by

where 0 < 1 − qT_s < 1, ε > 0, T_s is the sampling period and sat is the saturation function defined as follows

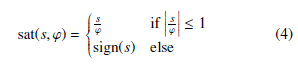with ϕ > 0 is the boundary layer width of s and sign is the sign function.

Using the reaching law (3) and the forward expression of the sliding function (2), the control law u(k) is given by

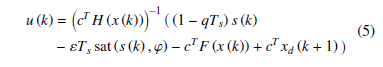3. Discrete-time Second Order Sliding Mode Control

The sliding function defined in [19,20] is given by

with β ∈ [0,1[ in order to ensure the stability of σ(k). The control law is given by

where u_eq(k) is the equivalent control used to force the system state to evolve on the sliding manifold and u_d(k) is the discontinuous control used to ensure the robustness.

Setting σ(k+1) = σ(k) = 0, the equivalent control u_eq(k) is determined from the following relation

4. Optimal Discrete-time Sliding Mode Control

4.1. Design of Sliding Surface

The sliding vector c^T is determined using the PSO algorithm in order to ensure the optimization of the closed-loop system response characteristics and the follow-up of the reference model in the presence of constraints on control input.

PSO algorithm starts with population of np ndimensional particles. The i^th particle of the swarm has a position x_i = x_i,1,…, x_i,n and a velocity v_i = vi,1,…,v_i,n. Its previously best visited position and the global best particle in the swarm are denoted by pbest_i = pbest ,…, pbest_i,n and gbest respectively. The velocity and the position of each particle are updated as follows

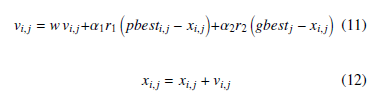with i = 1,…,np and j = 1,…,n. w is the inertia weight, α_1,2 are positive constant so-called the acceleration coefficients and r_1,2 are random parameters uniformly distributed within [0,1] at each generation.

PSO is used to generate the sliding vector that minimizes the following cost function

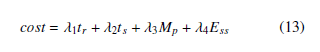where t_r is the rise-time, t_s is the settling-time, M_p is the overshoot, E_ss is the steady-state error and λ_q , q = 1,…,4, are their corresponding weights.

As illustrated in Table 1, the iterative process is repeated until stopping criterion is met.

Table 1: Description of PSO algorithm

Step 1          Parameter settings

Set the population size np, the minimum and maximum bounds xmin = xmin,1,…, xmin,n and x_max = x_max,₁,…, x_max,_n, and the acceleration coefficients α_1,2.

Step 2          Initialization

Initialize the particle’s position x_i⁰, i = 1…np, randomly and uniformly within bounds. Initialize the particle’s velocity v⁰_i and the particle’s best position to its initial position, i.e. pbest_i⁰ = x_i⁰.

Set gbest equal to the global best particle.

Step 3          PSO algorithm

WHILE stopping criterion is not met DO

Update the particle’s velocity and position

FOR i = 1 to np

FOR j = 1 to n

           vi,j                 =              wvi,j + α1r1 pbesti,j − xi,j             +

α2r2 gbestj − xi,j

END FOR xi = xi + vi

END FOR

Update the particle’s best position

FOR i = 1 to np

IF f (x_i) ≺ f (pbest_i) pbest_i = x_i

END IF

END FOR

Update the global best position

FOR i = 1 to np

IF f (pbest_i) ≺ f (gbest) gbest = pbest_i

END IF

END FOR

END WHILE

4.2. Design of Control Law

The control law is designed such that the chatter effect is avoided, the state trajectory convergences to the sliding surface after a finite-time interval and the closed-loop system is stable while respecting control constraints.

The forward expression of the sliding function (2) can

be rewritten as follows

Suppose that

For ku(k)k > u_max, the forward expression of the sliding function (14) is expressed by

For stability analysis, the Lyapunov function is chosen as follows

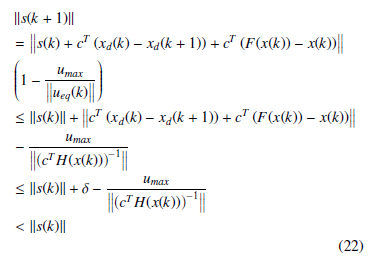Hence, s(k) decreases monotonically. From (18), the equivalent control u_eq (k) will belong to the constrained domain, i.e.   u_eq  u_max, in finite time and therefore it will bring the system trajectory to the sliding manifold s(k) = 0 on which the dynamics of the closed-loop system are stable.

5. Inverted Pendulum System

As shown in Figure 1, the inverted pendulum system consists of a pendulum amounted on a cart at a frictionless pivot point. The pendulum is of mass m = 0.1kg and length 2l = 1m and the cart is of mass M = 1kg [26]. u is the force applied to the cart that lies within the range of ±10N and g = 9.81m/s² is the gravity acceleration. The generalized coordinates are x and θ which represents the horizontal movement of cart and the rotation of pendulum respectively [27].

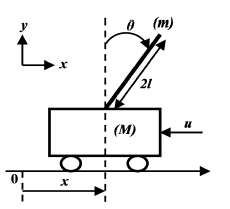Figure 1: Schematic of the inverted pendulum system

Let x = x₁ x₂ = θ θ˙ be the state vector. The dynamic equations are given by

6. Numerical Simulation Results

For T_s = 0.05s, the reference model is chosen as follows

The sliding vector and the reaching law parameters for DSMC controller are respectively

where w_max = 0.9 and w_min = 0.4 are the initial and final values of the inertia weight respectively, iter is the current iteration, and iter_max is the maximum number of iterations.

Figure 2 illustrates the evolution of the cost function (29) corresponding to ODSMC controller. It shows that PSO algorithm ensures a rapid convergence of the cost function to its minimum value of 0.236s corresponding to the following sliding vector

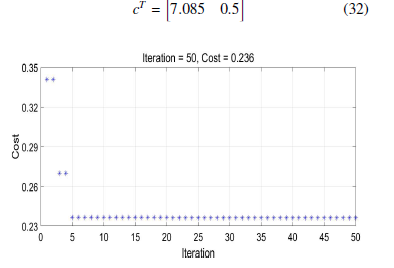Figure 2: Evolution of the cost function for ODSMC

Figure 3 shows numerical simulation results of ODSMC controller using the sliding vector (32). Figures 3a-3b present the state variables x_1,2(k) and their corresponding references x_d1,2(k). They show that the developed controller ensures the follow-up of the reference model and the stability of the closed-loop system in the presence of control input constraints. Figure 3c depicts the constrained control input u(k). It shows that chatter effect is avoided. Figure 3d illustrates the sliding function s(k). It shows that the state trajectory converges to the sliding surface in finite time.

• State variable x₁(k) and its reference x_d1(k)
• State variable x₂(k) and its reference x_d2(k)
• Control input u(k)
• Sliding function s(k)

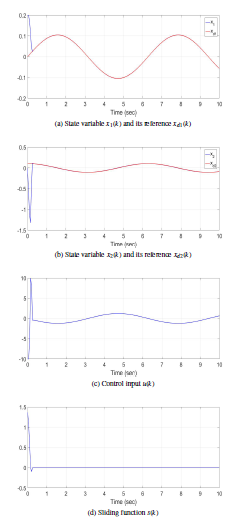Figure 3: Simulation results for ODSMC controller.

Figure 4 illustrates a comparison between DSMC with saturation function, DSOSMC and ODSMC controllers. Figure 4a presents a comparison of system responses y(k). It shows that all controllers ensure the follow-up of the reference model. Yet, the ODSMC controller ensures the fastest response time while respecting input constraints. Figure 4b depicts a comparison of control inputs u(k). It shows the effectiveness of the applied controllers in avoiding the chattering phenomenon. Moreover, the developed algorithm has lower values of control input in the initial phase than DSOSMC controller.

The results are summarized in Table 2. Actually, It shows that the developed ODSMC ensures the best results with the least rise and settling times of 0.14s and 0.24s respectively, and with lower values of control input than DSOSMC controller whose corresponding minimum and maximum input values are −20.6N and 12.18N respectively. Figure 4 and Table 2 demonstrate that ODSMC controller outperforms DSMC and DSOSMC controllers.

• Comparison of system responses
• Comparison of control inputs

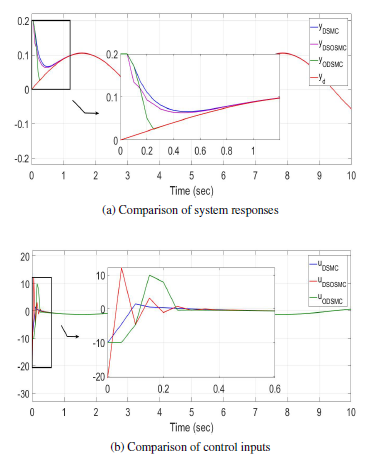Figure 4: Comparison between DSMC with saturation function, DSOSMC and ODSMC controllers.

Table 2: Summary table of numerical results

	Settling time (s)	Rise time (s)	umin	umax
DSMC	1.07	0.39	-10.07	1.5
DSOSMC	1.03	0.37	-20.6	12.18
ODSMC	0.24	0.14	-10	10

In this study, Matlab 2016a was used for the implementation of all algorithms.

7. Conclusion

This work presents an optimal discrete-time sliding mode controller for nonlinear SISO systems subject to input constraints. The particle swarm optimization algorithm is employed to determine the sliding vector for which the response characteristics are optimal and the closed-loop system model follows the reference model. Furthermore, the control law which is designed based on the equivalent control concept guarantees the avoidance of chattering phenomenon and the finite-time convergence of system trajectory to the sliding manifold on which the system dynamics are stable while respecting constraints. Simulation results demonstrate the efficiency of the developed controller in ensuring the fastest response comparing to discrete-time sliding mode controller using the saturation function and to discrete-time second order sliding mode controller. Future work will be to develop the proposed controller to multi-input multi-output nonlinear systems and to verify its effectiveness by experiments.

Conflict of Interest

The authors declare no conflict of interest.

1.  O. Jedda, A. Douik, “Optimal Discrete-Time Sliding Mode Control for Nonlinear Systems” in 15th International Multi-Conference on Systems, Signals & Devices (SSD), Hammamet Tunisia, 2018. 10.1109/SSD.2018.8570376
2.  C. Milosavljevic, “General Conditions for the Existence of a Quasi-Sliding Mode on the Switching Hyperplane in Discrete Variable Structure Systems” Autom. Remote Control, 14(3), 307-317, 1985.
3.  K. Furuta, “Sliding Mode Control of a Discrete System” Systems & Control Letters, 14(2), 145-152, 1990. https://doi.org/10.1016/0167-6911(90)90030-X
4.  G. Golo, C. Milosavljevic, “Robust Discrete-time Chattering Free Sliding Mode Control” Systems & Control Letters, 41(1), 19-28, 2000. https://doi.org/10.1016/S0167-6911(00)00033-5
5.  S. Z. Sarpturk, Y. Istefanopulos, O. Kaynak, “On the Stability of Discrete-time Sliding Mode Control Systems” IEEE Trans. Autom. Control, 32(10), 930-932, 1987. 10.1109/TAC.1987.1104468
6.  Y. Niu, D. W. Ho, Z. Wang, “Improved sliding mode control for discrete-time systems via reaching law” IET Control Theory Appl., 4(11), 2245-2251, 2010. 10.1049/iet-cta.2009.0296
7.  J. Hu, Z. Wang, H. Gao, L. K. Stergioulas, “Robust H sliding mode control for discrete time-delay systems with stochastic nonlinearities” J. Frankl. Inst., 349(4), 1459-1479, 2012. https://doi.org/10.1016/j.jfranklin.2011.05.018
8.  M. C. Pai, “Discrete-time sliding mode control for robust tracking and model following of systems with state and input delays” Nonlinear Dyn., 76(3), 1769-1779, 2014. https://doi.org/10.1007/s11071-014-1245-0
9.  H. Du, X. Yu, M. Z. Chen, S. Li, “Chattering-free discretetime sliding mode control” Automatica, 68, 87-91, 2016. https://doi.org/10.1016/j.automatica.2016.01.047
10.  B. Bandyopadhyay, F. Deepak, K. S. Kim, Sliding Mode Control Using Novel Sliding Surfaces, Springer, 2009.
11.  I. U. VADIM, “Survey paper variable structure systems with sliding modes” IEEE Trans. Autom. Control, 22(2), 1977.
12.  K. D. Young, V. I. Utkin, U. Ozguner, “A Control Engineers Guide to Sliding Mode Control” IEEE Trans. Control Syst. Technol., 7(3), 328-342, 1999. 1063-6536(99)03275-3
13.  W. Perruquetti, J. P. Barbot, Sliding Mode Control in Engineering, M. Dekker, 2002.
14.  W. Gao, Y. Wang, A. Homaifa, “Discrete-time Variable Structure Control Systems” IEEE Trans. Ind. Electron., 42(2), 117-122, 1995. 10.1109/41.370376
15.  J.-h. Kim, S.-H. Oh, J. K. Hedrick, “Robust Discrete-time Variable Structure Control Methods” J DYN SYST-T ASME, 122(4), 766-775, 2000. 10.1115/1.1320448
16.  J.-h. Kim, D.-i. D. Cho, “Discrete-time Variable Structure Control using Recursive Switching Function” in Proceedings of the 2000 American Control Conference, Chicago IL USA, 2000. 10.1109/ACC.2000.876673
17.  O. Jedda, A. Douik, “Discrete-time Integral Sliding Mode Control with Anti-windup” Studies in Informatics and Control, 27(4) 413-422, 2018. https://doi.org/10.24846/v27i4y201805
18.  A. Y. Alanis, N. Arana-Daniel, C. Lopez-Franco, E. N. Sanchez,“PSO-gain Selection to Improve a Discrete-time Second Order Sliding Mode Controller” in IEEE Congress on Evolutionary Computation, Cancun Mexico, 2013. 10.1109/CEC.2013.6557672
19.  M. Mihoub, A. S. Nouri, R. B. Abdennour, “The Multimodel Approach for a Numerical Second Order Sliding Mode Control of Highly non Stationary Systems” in American Control Conference, Seattle WA USA, 2008. 10.1109/ACC.2008.4587240
20.  M. Mihoub, A. S. Nouri, R. B. Abdennour, “Real-time Application of Discrete Second Order Sliding Mode Control to a Chemical Reactor” Control Eng. Pract., 17(9), 1089-1095, 2009. https://doi.org/10.1016/j.conengprac.2009.04.005
21.  G. Bartolini, A. Ferrara, V. I. Utkin, “Adaptive Sliding Mode Control in Discrete-time Systems” Automatica, 31(5), 769-773, 1995. https://doi.org/10.1016/0005-1098(94)00154-B
22. B. Castillo-Toledo, S. Di Gennarob, A.G. Loukianov, J. Rivera, “Discrete time Sliding Mode Control with Application to Induction Motors” Automatica, 44(12), 3036-3045, 2008. doi:10.1016/j.automatica.2008.05.009
23.  J. Kennedy, R. Eberhart, “Particle Swarm Optimization” in Proceedings of IEEE International Conference on Neural Networks, Perth Australie, 1995. 10.1109/ICNN.1995.488968
24.  J. C. Bansal, P. Singh, M. Saraswat, A. Verma, S. S. Jadon, A. Abraham, “Inertia Weight Strategies in Particle Swarm Optimization” in 3rd World Congress on Nature and Biologically Inspired Computing, Salamanca Spain, 2011. 10.1109/NaBIC.2011.6089659
25.  D. P. Rini, S. M. Shamsuddin, S. S. Yuhaniz, “Particle Swarm Optimization: Technique, System and Challenges” Int. J. Comput. Appl., 14(1), 19-26, 2011. 10.5120/ijais-3651
26. L. X. Wang, “A Supervisory Controller for Fuzzy Control Systems that Guarantees Stability” IEEE Trans. Autom. Control, 39(9), 1845-1847, 1994. 10.1109/9.317109
27.  O. Jedda, J. Ghabi, A. Douik, “Sliding Mode Control of an Inverted Pendulum” In Applications of Sliding Mode Control, Springer Singapore, 105-118, 2017.
28.  J. Xin, G. Chen, Y. Hai, “A Particle Swarm Optimizer with Multistage Linearly-Decreasing Inertia Weight” in International Joint Conference on Computational Sciences and Optimization (CSO),Sanya Hainan China, 2009. 10.1109/CSO.2009.420
29.  Y. Shi, R. C. Eberhart, “Empirical Study of Particle Swarm Optimization” in Proceedings of the 1999 Congress on Evolutionary Computation, Washington DC USA, 1999. 10.1109/CEC.1999.785511

(Click Here)

(Click Here)