1. Introduction

Facility layout design plays a large part in business competition. Facilities can be machines, workstations, construction sites or departments, depending on the type of business. Costs can be reduced by having an appropriate layout. However, it is a complex problem. One of the essential goals of the design is to minimize total material handling costs, which are affected by many factors, such as types of materials, processing and production flow. Especially in the manufacturing industries, some produce not just one product but a variety of goods.

Moreover, in reality, the factors that affect material handling costs are vague and fuzzy. In a manufacturing system, they are dependent generally on the seasons, product variety and business growth. In order to engage with this ambiguity, there are levels of the vagueness of information, and the decision is usually made under uncertainty [1]. Fuzzy sets theory is a suitable concept to deal with this situation [2-6]. Therefore, this paper extends the research to understand the effects when the values in fuzzy sets are predictable and if they are extremely vague.

In many manufacturing industries, there can be several products manufactured in a factory, and each product can have different routes through machines or workstations. Production efficiency depends highly on this kind of problem in production planning [7]. Production costs can be reduced by 10–30% when the facility layout is more effective [8]. Shorter handling distances of materials’ flow between workstations are required for faster transfer times within a factory floor.

The inputs necessary to design a facility layout for an actual production system are usually imprecise. Besides, the issue is considered a complicated situation because of the choice of products, materials, processes and other factors involved with the business. These factors are also time-dependent, such as customer orders and product growth, so the cost of material handling between machines usually changes. Different methods [9-12] have been presented for solving these kinds of problems; however, uncertain and ambiguous data inputs have been paid little attention [13]. Therefore, the fuzzy set theory is applied in this paper.

Many researchers have proposed different ways to solve this complex problem. In choosing the solution, the aim should be to achieve maximum efficiency, and there should be a simple method for finding the answer. Drira, et al. [14] gathered techniques and methods used for solving machine layout problems. Several methods can be used in the analysis of these problems, such as branch and bound, dynamic programming, simulated annealing, tabu search, genetic algorithms, ant colony, intelligence methods.

To find a solution with accurate answers to a complex problem, the costs of solving are very high [15]. Thus, it is better, rather, to have a method that can solve the vague problem obtaining an acceptable answer with less time and cost than that with high accuracy and high cost. Since mathematical modeling techniques used to solve the facility layout design problem are complicated, challenging, and time-consuming, the issues require a powerful technique [5].

For the problems of machine layout design, the genetic algorithm is one popular method for finding answers, or approximate answers [16]. The Simple Genetic Algorithm (SGA) applies the principle of evolution and natural selection, by which the best individuals are selected to generate answers for the next generation. To calculate the answer by SGA is fundamental to solving the optimization problem. Many studies adopting this method have been released [14].

Conventionally, Genetic Algorithm (GA) includes these steps: generate an initial population, select high potential chromosomes to be parents, crossover and mutate parents’ chromosomes to produce offspring chromosomes. Since there are a couple of genetic operators used in GA steps, improving the results fulfilling genuine applications can be achieved by adopting some of these operators (see [17-19] and [20]). The action of selecting high potential chromosomes to be parents called the selection process is the operation that has been broadly studied. Tournament Selection (TOS) and Roulette Wheel Selection (RWS) are general ways for making a selection. It was suggested that TOS is more effective than RWS [21-23]; the consequence is that a reasonable answer can be reached faster.

The research of Vitayasak [24] on fuzzy methods is interesting. The fuzzy approach can help manage uncertainty in practice, which may arise from a lack of information, not having enough data for the application, or the data not yet being available [25]. The experience of experts in reasoning or decision making in the human situation can help analysis and help manage uncertainty. The fuzzy theory is a theory of uncertain boundaries. Currently, it is widely used in the study of problems containing uncertain information [26].

      It is important for machine layout design decision making and an efficient way to deal with inaccurate and vague information. Kritwattanakorn, et al. [27] used the RWS method for the selection approach in GA and suggested not to apply mutation for machine layout problems. However, based on the suggestions given by some research [21-23], the TOS method seems to be superior in finding a solution qualitatively (for instance, minimizing the total material handling cost) and obtain answers faster and closer to the optimum. In our paper presented initially to a conference [28], we related to the research of Kritwattanakorn, et al. [27] that not to apply mutation, used TOS for selection, and showed how to deal with the vagueness of information and assist solving problems taken from earlier research works [25, 26]. Our proposed method performed corresponding to the work presented by  Jinghui, et al. [21] that using TOS is competitive in terms of solution quality and achieving minimization faster.

      However, realistically, there are also levels of the vagueness of information. To understand the effects when the values in fuzzy sets are predictable and if they are extremely vague, in this study, the tournament method was used in the selection process for the genetic algorithms solving the machine layout problem. Material handling information was considered employing fuzzy uncertainty. An original layout and new layouts constructed from three GA based approaches were compared for 2 case studies. The first was the case where fuzzy information was thought predictable, examining different forms of skewed shapes. In the second case, the fuzzy data was obtained from a process expert in a new factory when asked to give the possible values for each variable. Thus the fuzzy sets were utterly formless. Every approach in the study was programmed and run with Visual Basic for Applications in Microsoft Excel for determining the layout, distance, and cost.

2. Methods

      The fitness function, which is a particular type of objective function, is required for the GA algorithm to execute optimization. In this paper, the objective (1) is to minimize the total costs of material handling. This objective has been chosen by many researchers [29-31] in determining facility layouts. The function can be written as

In the calculation, minimize C is the objective, the variables used in consideration in this paper,  and  are considered as crisp numbers, and  is information that is uncertain.

In general, . However, in this study the information was considered both as if it is fuzzy to compare with the conventional idea, and as if it is crisp. Thus, when the frequency and the volume of material flows are considered as fuzzy numbers, they will be represented as  and , respectively, and the material handling flow as a fuzzy number is  (3).

Since the total cost, , is a crisp number,  needs to be converted back to be an exact number. This method is called defuzzification, see (4).

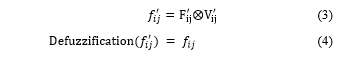However, in some cases, the materials frequency and volume flow information are exact numbers, so they need to be converted to a fuzzy number. This method is called fuzzification (5) when  is a number.

The framework:

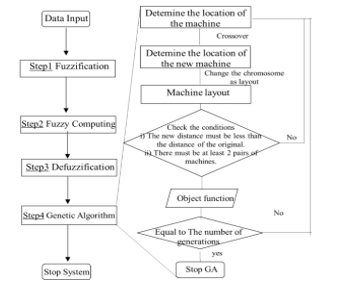
• Data input: the data input includes the production routing of each product (), number of machines (), sizes of machines (width , and length, ), shop floor area (W is width and L is length), frequency of material flow per round (), volume flow per unit (), unit material handling cost between locations of machines () and distance between machines ( , population size ) and the number of generations to simulate ( ).
• Step 1) Fuzzification: The uncertain flow frequency of materials, which is the function of and , was converted to fuzzy numbers ( ).
• Step 2) Fuzzy computing: Fuzzy arithmetic was used.
• Step 3) Defuzzification: In order for the next step following the GA approach, crisp numbers are essential for calculation. The fuzzy number was required to be transformed into crisp numbers.
• Step 4) Genetic algorithm: The sub-processes in the adapted GA are shown in Fig. 2.
• Stop: The calculation stops when conditions are met as in Fig.

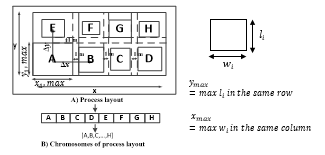Figure 1: Chromosomes representation.

Figure 2: The framework.

2.1.  Fuzzy number

      Fuzzy numbers are the foundation of fuzzy set theory [2]. They are an extended form of real numbers that do not refer to one single value, but a set of possible crisp numbers. The fuzzy technique is used to represent data with uncertainties.

2.1.1. The shape of membership: Triangular fuzzy numbers (TFNs), graphically represented as Fig. 3, are used in this research. They are suitable because of their computational advantages and commonly used for subjective description [6].

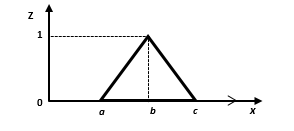Figure 3: Triangular fuzzy number.

The membership function of a TFN can be explained by:

is the grade of membership,

where

or

“highest grade of membership at the modal value.”

Therefore,

a = the lowest possible value,

b = the most likely possible value,

c = the highest possible value in the fuzzy set.

2.2.2. Fuzzification: First, it is necessary to convert the input information to fuzzy numbers and calculate them using fuzzy operators. For input data  and , the fuzzy sets of  and  are

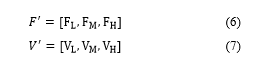 and  are the lowest, most likely, and highest possible values of the frequency flow and  and are the lowest, most likely and highest possible values of the volume flow, and their grades of membership are between 0 and 1. If, for example, the total material flow frequency of all products is possibly 20 times and the total material flow volume is approximately 5 units each time, the material flow F could be a set of numbers with the most likely value of 18 such as [16, 18, 19] as well as V could be [3, 5, 6].

2.1.3. Fuzzy arithmetic: The operations  [32] can be indicated by

Fuzzy addition :

Fuzzy multiplication :

2.1.4. Defuzzification: Before entering the GA procedure, the fuzzy numbers for the material flow must be changed to crisp numbers using the fuzzy weight method [33].

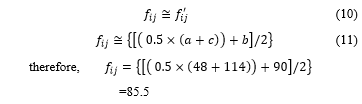2.2.  Genetic algorithm

The objective function (1) is used in this paper to find the optimum value by applying the genetic algorithm. The suggested GA has been modified from the Simple Genetic Algorithm (SGA) [16]. It begins with an initial set of random solutions for the problem being considered. The set of these alternatives is called the population. The population’s individuals are called chromosomes. The objective function evaluates the results from the chromosomes. The chromosomes showing high potential is then carried out to be a part of the new generation. In the crossover phase, a chromosome is chosen, along with the checking conditions, to produce the offspring. The details follow.

2.2.1. Initialization: GA approach begins with creating an initial population, . In our cases for solving machine layout problems, the genes represent the machines, and the chromosomes are for the layouts. Thus,  the initial population can be converted from the “prior to improvement” process layout, see Fig. 1 (B) for an example.

2.2.2. Fitness evaluation: This is the procedure for assessing the chromosome’s value. The chromosome that is more likely to be selected for the reproduction process would be selected by taking the proportionate fitness into consideration. The objective function of the fitness function, as presented in (12), can be described by total distance, in order to minimize the total costs of the material handling in the machine design issue.

Every material handling distance of product P is computed from the machine routing when each row or column of the machines is 1 m apart, as shown in Fig. 1. Assuming that there are 3 products required to be manufacture in a plant, as shown in Table 2, thus k=3. The machines have to be arranged on the floor plan to determine the total distance derived for a chromosome. The machines were arranged onto a certain floor area of W ´ L. The difference between the number of columns and rows of the machines was 1 at most.

2.2.3. Selection: This step decides which chromosomes should be parents in the reproduction process to generate offspring for the next generation.

Tournament selection (TOS): The simple tournament selection method [14] was used in this research. First, it divides the population into groups. Next, in each group, n chromosomes are randomly selected. The next generation of parents shall then be assigned from the chromosomes that make the most efficient solution in their groups. There were 2 groups in a tournament in this work. Each group had 3 chromosomes (n = 3), then the best chromosomes in each group were chosen as the next generation of parents.

2.2.4. Crossover: A new solution, namely offspring, is created by the crossover process. In this work, a crossover point, as shown in Fig. 4, was randomly chosen. After the crossover process, 2 conditions were checked. For condition 1, at least 2 pairs of machines in the chromosome must be operated side-by-side. For condition 2, after simulating the machines onto the shop floor area, and the new distance derived from the offspring must be reduced in comparison to the distance achieved by the layout of the parent.

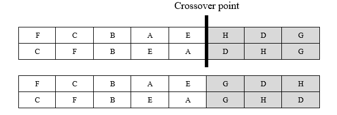Figure 4: One point crossover process.

2.2.5. Mutation: The mutation process is one in which genes are randomly selected and their positions in the chromosome are swapped to generate additional offspring. It is a traditional step in conventional GA. Kritwattanakorn et al. [27], however, proposed that the mutation should be disregarded in this kind of problem. They have found it produced machines positioned further away while they should be put side by side when considering routing and lastly produced poor outcomes.

2.2.6. Stop:  The proposed GA procedure was looped until the given number of generations was met, see Fig. 2.

3. Example

Two layout problems were studied in this research. The details are as follows:

• Case 1: This case uses original information from the manufacture of plywood furniture. There were 3 products and 8 machines in the same shop floor area. Table 2 shows the production routing for each product. Table 3 exhibits the sizes of the machines. The material handling information was initially received as crisp numbers.
• Case 2: This case studied a bus manufacturer. The fuzzy material handling information was given when their process experts were asked for the values in the fuzzy sets of material flow between machines. There were 12 products and 8 machines. Table 4 shows the production routing of each product, and the machine sizes are shown in Table 5.

Since GA is widely applied for solving machine layout problems, the layouts constructed by different approaches were compared as listed. A summary of GA based approaches is shown in Table 1.

1. Initial layout (unknown approach)
2. SGA [16]
3. Modified GA with RWS and additional conditions (Kritwattanakorn et al. [27])
4. Modified GA with TOS and additional conditions (proposed approach)

Table 1: Summary of GA based approaches.

No	Information	Selection	Crossover	Mutation	Special Conditions
1	Crisp	Unknown (Initial layout)
2	Crisp	RWS	One point	One point swap	No
3	Crisp	RWS	One point	No	Yes, see 2.2.4
4	Fuzzy	TOS	One point	No	Yes, see 2.2.4

Here the proposed GA approach used Thai Baht (32.50 THB = 1 USD), the number of the initial population, , was 10, and the number of generations, , was 100 given to stop the loop. The machine layout design problems were solved using VBA in MS Excel running under Windows 8 OS, on an Intel (R) Core (TM) i7-4500U 1.8GHz  Ram 4 GB device.

Table 2: Products and production routing for case 1.

Product	Production Routing
1	A-B-C-D
2	A-E-F-G
3	A-H

Table 3: Sizes of the machines for case 1.

Machine	Dimensions
	Width (m)	Length (m)
A	2.00	2.00
B	1.35	1.30
C	1.30	1.25
D	1.35	1.30
E	1.22	1.25
F	1.00	1.00
G	1.22	1.25
H	1.20	1.22

4. Results and Discussion

4.1.  Case 1: When the level of fuzziness was considered predictable.

In case 1, the costs from layouts exposed by the existing methods including: from the SGA method [16], the adapted GA that applied GA with RWS selection and without mutation [27], and the proposed method in this study using 6 different fuzzy data sets combined with the GA approach (Fig. 5). The case studies used various fuzzy set differences of 0%, 15%, 30%, and 50% fuzziness for the frequency flow and volume flow. The fuzzy set with the difference of 0% represents a crisp number.

Table 4: Products and production routing for case 2.

Product	Production Routing
1	A – F
2	B – C
3	A – F
4	B – D
5	A – G
6	B – H
7	A – G – H
8	B – G – H
9	A – E – F
0	B – E – C
11	A – E – F
12	B – E – D

Table 5: Sizes of the machines for case 2.

Machine	Dimensions
	Width (m)	Length (m)
A	1.20	1.50
B	1.20	1.50
C	1.70	1.50
D	1.20	1.40
E	1.50	1.20
F	1.30	6.00
G	1.20	1.00
H	3.50	2.00

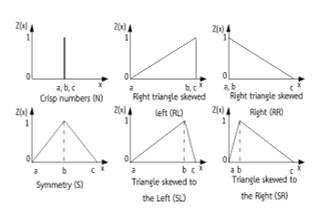Figure 5: Data sets representing fuzzy numbers.

The results in Fig. 6 show that the total costs vary if the input information is uncertain or fuzzy. If there is the high difference between the lowest and highest possible values, the total costs increase or decrease considerably, such as for the right triangle skewed right (RR), the highest possible value gives a high total cost, but the lowest possible value gives a low total cost. The costs increase or decrease depending on the nature of the skew. If the input information is skewed fully to one side (such as RR and SR), it is likely to make the total costs higher, but if the input is skewed to the minimal side (such as RL and SL), it shows the opposite impact.

Table 6: Results of case 1 with different fuzzy types.

Difference	Fuzzy Type	,	Total Cost (USD)
0% a	N	[20, 20, 20], [5, 5, 5]	914.46
15%	S	[18, 20, 22], [4, 5, 6]	923.61
	RL	[17, 20, 20], [4, 5, 5]	841.30
	RR	[20, 20, 23], [5, 5, 6]	1,001.34
	SL	[18, 20, 21], [4, 5, 5]	861.88
	SR	[19, 20, 22], [5, 5, 6]	976.19
30%	S	[17, 20, 23], [4, 5, 6]	955.61
	RL	[14, 20, 20], [3, 5, 5]	781.86
	RR	[20, 20, 26], [5, 5, 7]	1,101.93
	SL	[16, 20, 22], [3, 5, 6]	868.74
	SR	[18, 20, 24], [4, 5, 7]	1,005.91
50%	S	[15, 20, 25], [3, 5, 7]	960.18
	RL	[10, 20, 20], [2, 5, 5]	731.57
	RR	[20, 20, 30], [5, 5, 8]	1,234.52
	SL	[13, 20, 23], [2, 5, 7]	884.74
	SR	[17, 20, 27], [3, 5, 8]	1,067.63

a. Crisp number

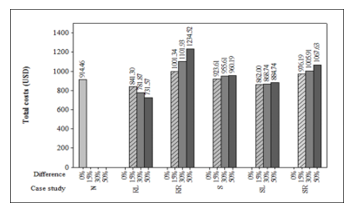Figure 6: The relationship between various fuzzy data sets and the total cost.

From the findings of this case, it can be seen that the suggested technique shows total costs that increase or decrease depending on the flow of the material handling system in the production. These findings agree with the existing research works [9-12] that information is essential for making a decision on layout planning and design, and fuzzy sets is an appropriate idea in dealing with imprecise information [25, 26].

Table 6 shows the outcomes of the 4 different methods and their layouts for the machines are shown in Fig. 7. Table 6 demonstrates the results of total costs and distances. Before arranging the layout, the total cost initially was 1,179 USD and the total distance was 38.45. The proposed method with a different variation of 15% in fuzzy data input (due to natural associated vagueness) has a total cost of 923.61 USD and a total distance of 29.72 m. It can reduce the total cost by 21.66% and the distance by 22.71%. Both the traditional GA (SGA) method [16] and the Kritwattanakorn et al. method [27] give total costs and distances greater than the proposed method.

Table 7: Comparison of the different approaches in case 1.

Approach	Total cost (USD)	Total Distance (m)
Unknown (initial layout)	1,179.00	38.45
SGA	1,060.92	34.48
Modified GA+RWS+Conditions	978.46	31.80
Modified GA+TOS+Conditions *	923.61	29.72

* Fuzziness at 15 % difference

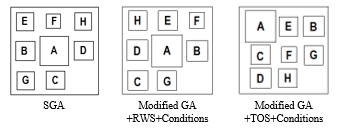Figure 7: Layouts of machines obtained using different methods for case 1.

4.2.  Case 2: When the level of fuzziness was extremely vague.

In fact, the shape of fuzzy sets might not be specific. This study used a bus manufacturer as an example. They are a family run business. Machines were laid out based on the experience of the systems expert, not an analysis of manufacturing data. Table 8 shows the frequency and volume of material transport between machines, by letting the expert respond what were the minimum, modal, and maximum values, as for the machine layout design input.

Table 8: Fuzzy data input of case 2.

Machine	Frequency flow (	Volume flow  (
M1-M5	[3, 10, 16]	[5, 16, 22]
M1-M6	[6, 8, 14]	[7, 10, 24]
M1-M7	[3, 4, 7]	[8, 12, 18]
M2-M3	[1, 1, 1]	[0, 2, 2]
M2-M4	[3, 6, 8]	[6, 8, 14]
M2-M5	[2, 2, 4]	[7, 8, 13]
M2-M8	[1, 3, 4]	[1, 2, 2]
M5-M3	[3, 6, 8]	[6, 8, 14]
M5-M6	[2, 2, 5]	[6, 11, 15]
M7-M8	[2, 2, 2]	[3, 4, 6]

Table 9 shows the results that the totals cost of material handling can be considerably lowered. The costs generated from the layouts obtained from the method described in this paper were compared competitively with the initial machine layout and 2 existing methods. The machine layouts can be seen in Fig. 8. Table 9 compares the approaches. The total cost and the total distance before arranging being 84.22 USD and 103.10 m, respectively. The proposed method, with fuzzy data input acknowledged from the product experts, has a total cost and distance of 66.40 USD and 82.45 m, correspondingly. The total cost and distance can be reduced by 21.16% and 20.03%.

Even if the total cost obtained from the proposed method was higher than SGA [16] and the method with RWS (Kritwattanakorn et al. method [27]), the total distance was the shortest. This emphasizes the effect of fuzziness of information on decision making. More attention should be paid to uncertainties of data.

Table 9: Comparison of the different approaches in case 2

Approach	Total cost (USD)	Total Distance (m)
Unknown (initial layout)	84.22	103.10
SGA	48.56	92.40
Modified GA+RWS+Conditions	41.24	90.25
Modified GA+TOS+Conditions	66.40	82.45

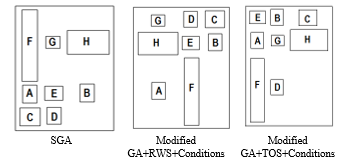Figure 8: Layouts of machines obtained using different methiods for case 2.

5. Conclusion

It is possible to obtain a proper machine layout by adapting the genetic algorithm. Tournament selection is a powerful technique that helps GA to discover a suitable solution faster. It was found that the total distance is shorter by following the proposed method. Applying fuzzy numbers is the proper method to cope with imprecise information. This research considered fuzzy numbers for representing material handling inputs as so the situations of unclear information can be reflected realistically. If the uncertainty of data occurs, it can either increase or decrease the total cost. It shows that the input ambiguity markedly affects the total material handling costs. This increases awareness of the use of uncertainty information.

Conflict of Interest

The authors declare no conflict of interest.

Acknowledgment

This research was supported by grants funded by the Graduate School of Manufacturing Engineering, Suranaree University of Technology, and the Ministry of Science and Technology, Thailand.

1.  L. A. Zadeh, “Fuzzy Sets as a Basis for a Theory of Possibility,” Fuzzy Sets and Systems, 100, 9-34, 1999. https://doi.org/10.1016/S0165-0114(99)80004-9
2.  L. A. Zadeh, “Fuzzy Sets,” Information and Control, 8, 338-353, 1965. https://doi.org/10.1016/S0019-9958(65)90241-X
3. İ. Kaya, M. Çolak, and F. Terzi, “A Comprehensive Review of Fuzzy Multi Criteria Decision Making Methodologies for Energy Policy Making,” Energy Strategy Reviews, 24, 207-228, 2019. https://doi.org/10.1016/j.esr.2019.03.003
4.  A. L. Guiffrida and R. Nagi, “Fuzzy Set Theory Applications in Production Management Research: A Literature Survey,” Journal of Intelligent Manufacturing, 9, 39-56, 1998. 10.1023/a:1008847308326
5.  B. K. Wong and V. S. Lai, “A Survey of the Application of Fuzzy Set Theory in Production and Operations Management: 1998–2009,” International Journal of Production Economics, 129, 157-168, 2011. https://doi.org/10.1016/j.ijpe.2010.09.013
6.  S. Balin, “Parallel Machine Scheduling with Fuzzy Processing Times Using a Robust Genetic Algorithm and Simulation,” Information Sciences, 181, 3551-3569, 2011. https://doi.org/10.1016/j.ins.2011.04.010
7.  M. Ficko, M. Brezocnik, and J. Balic, “Designing the Layout of Single- and Multiple-Rows Flexible Manufacturing System by Genetic Algorithms,” Journal of Materials Processing Technology, 157–158, 150-158, 2004. http://doi.org/10.1016/j.jmatprotec.2004.09.012
8. J. A. Tompkins, J. A. White, Y. A. Bozer, and J. M. A. Tanchoco, Facilities Planning: Wiley, 2010.
9.  F. M. Defersha and A. Hodiya, “A Mathematical Model and a Parallel Multiple Search Path Simulated Annealing for an Integrated Distributed Layout Design and Machine Cell Formation,” Journal of Manufacturing Systems, 43, 195-212, 2017. https://doi.org/10.1016/j.jmsy.2017.04.001
10.  P. B. G. S. N. Murthy, J. Ranganayakulu, K. P. Vidhu, and K. V. Rao, “Heuristic Search Algorithm for the Single-Row Machine Layout in an Automated Manufacturing System,” Procedia Technology, 25, 1088-1095, 2016. https://doi.org/10.1016/j.protcy.2016.08.213
11.  Y. Ojaghi, A. Khademi, N. M. Yusof, N. G. Renani, and S. A. H. b. S. Hassan, “Production Layout Optimization for Small and Medium Scale Food Industry,” Procedia CIRP, 26, 247-251, 2015. https://doi.org/10.1016/j.procir.2014.07.050
12.  M. A. El-Baz, “A Genetic Algorithm for Facility Layout Problems of Different Manufacturing Environments,” Computers & Industrial Engineering, 47, 233-246, 2004. https://doi.org/10.1016/j.cie.2004.07.001
13.  S. Safarzadeh and H. Koosha, “Solving an Extended Multi-Row Facility Layout Problem with Fuzzy Clearances Using Ga,” Applied Soft Computing, 61, 819-831, 2017. https://doi.org/10.1016/j.asoc.2017.09.003
14.  A. Drira, H. Pierreval, and S. Hajri-Gabouj, “Facility Layout Problems: A Survey,” Annual Reviews in Control, 31, 255-267, 2007. https://doi.org/10.1016/j.arcontrol.2007.04.001
15.  F. Karray, E. Zaneldin, T. Hegazy, A. Shabeeb, and E. Elbeltagi, “Computational Intelligence Tools for Solving the Facilities Layout Planning Problem,” in Proceedings of the 2000 American Control Conference. ACC (IEEE Cat. No.00CH36334), 3954-3958, 2000.
16.  J. H. Holland, Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence: MIT press, 1992.
17.  N. M. Razali and J. Geraghty, “Genetic Algorithm Performance with Different Selection Strategies in Solving Tsp,” in World congress on engineering 2011, London, U.K., 1134-1139, 2011.
18.  M. Gen, K. Ida, and C. Cheng, “Multirow Machine Layout Problem in Fuzzy Environment Using Genetic Algorithms,” Computers & Industrial Engineering, 29, 519-523, 1995. https://doi.org/10.1016/0360-8352(95)00127-M
19.  R. Tavakkoli-Moghaddain and E. Shayan, “Facilities Layout Design by Genetic Algorithms,” Computers & Industrial Engineering, 35, 527-530, 1998. https://doi.org/10.1016/S0360-8352(98)00150-8
20. H. M. Pandey, “Performance Evaluation of Selection Methods of Genetic Algorithm and Network Security Concerns,” Procedia Computer Science, 78, 13-18, 2016. https://doi.org/10.1016/j.procs.2016.02.004
21.  Z. Jinghui, H. Xiaomin, Z. Jun, and G. Min, “Comparison of Performance between Different Selection Strategies on Simple Genetic Algorithms,” in International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC’06), Vienna, Austria, 1115-1121, 2005. 10.1109/cimca.2005.1631619
22.  H. Kılıç and U. Yüzgeç, “Tournament Selection Based Antlion Optimization Algorithm for Solving Quadratic Assignment Problem,” Engineering Science and Technology, an International Journal, 22, 673-691, 2019. https://doi.org/10.1016/j.jestch.2018.11.013
23.  H. Kılıç and U. Yüzgeç, “Improved Antlion Optimization Algorithm Via Tournament Selection and Its Application to Parallel Machine Scheduling,” Computers & Industrial Engineering, 132, 166-186, 2019. https://doi.org/10.1016/j.cie.2019.04.029
24.  S. Vitayasak, “Facility Layout Problem: A 10-Year Review and Research Perspectives (in Thai),” Naresuan University Engineering Journal, 5, 46-62, 2010.
25.  Z. Güngör and F. Arıkan, “Application of Fuzzy Decision Making in Part-Machine Grouping,” International Journal of Production Economics, 63, 181-193, 2000. https://doi.org/10.1016/S0925-5273(99)00010-9
26.  S. K. Deb and B. Bhattacharyya, “Fuzzy Decision Support System for Manufacturing Facilities Layout Planning,” Decision Support Systems, 40, 305-314, 2005. https://doi.org/10.1016/j.dss.2003.12.007
27.  S. Kritwattanakorn, K. Chamniprasart, and W. Boongsood, “A Permutation-Based Genetic Algorithm for Solving the Machine Layout of Manufacturing System,” in The 10th SEATUC Symposium, Tokyo, Japan, 2016.
28.  C. Jadram and W. Boongsood, “Application of Fuzzy Materials-Handling Inputs with the Genetic Algorithm for Machine Layout,” in 2018 7th International Conference on Industrial Technology and Management (ICITM), Oxford, UK, 265-269, 2018. 10.1109/icitm.2018.8333958
29.  R. G. Askin and C. R. Standridge, Modeling and Analysis of Manufacturing Systems: Wiley, 1993.
30.  C. K. H. Lee, “A Review of Applications of Genetic Algorithms in Operations Management,” Engineering Applications of Artificial Intelligence, 76, 1-12, 2018. https://doi.org/10.1016/j.engappai.2018.08.011
31. W. Yi, H.-L. Chi, and S. Wang, “Mathematical Programming Models for Construction Site Layout Problems,” Automation in Construction, 85, 241-248, 2018. https://doi.org/10.1016/j.autcon.2017.10.031
32. S. Gao and Z. Zhang, “Multiplication Operation on Fuzzy Numbers,” Journal of Software, 4, 331-338, 2009.
33. W. Dong and F. S. Wong, “Fuzzy Weighted Averages and Implementation of the Extension Principle,” Fuzzy Sets and Systems, 21, 183-199, 1987. https://doi.org/10.1016/0165-0114(87)90163-1

(Click Here)

(Click Here)