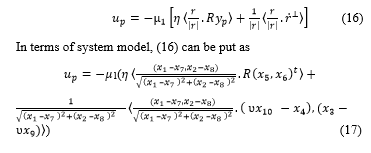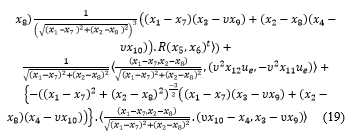1. Introduction

Pursuit evasion game (PEG) is widely prevalent in nature. It is a game that is considered to be between the pursuer and an evader. PEG can be observed among animals when they chase a victim or when they battle for territory and even when they mate. In the context of engineering, PEG finds application in missile guidance and avoidance, aircraft pursuit and evasion, maritime asset protection etc.[1].

Initial study of PEG was mainly from the point of view of game theory [2]. PEG was further studied from the point of view of geometric control theory in [3]. Pursuit manifold is defined in terms of certain criteria involving relative distance and relative velocity between the pursuer and the evader. Using a control law which enables the pursuer to reach the pursuit manifold in an optimum way and keeping the pursuit invariant on the manifold, [3] studied three strategies found in nature, viz., motion camouflage (CM), constant bearing (CB) and classical pursuit (CP). The objective of the work reported in [3] is to find a justification for the prevalent use of CM in PEG in nature. It turned out that, keeping the speed of the pursuer and the evader constant and ensuring that the pursuer moves faster than the evader, [3] has been able to show through evolutionary games that CB and CP strategies always converge to CM strategy under certain fixed assumptions on evader motion thus supporting what is seen in nature.

However, Pais [4] has argued that if the evader control law is reactive (i.e. it is in some way dependent on the baseline vector joining the pursuer and evader locations and its rate of change), then the conclusions in [3] might not hold good. Wei [5] has dropped the constant speed assumption of both the pursuer and evader and allowed the pursuer to change its acceleration as required. Wei also introduced the case of victim turning suddenly left or right when the pursuer comes too close to the evader. A related problem to PEG of confinement and escape is addressed in [6].

Our aim in this paper is this. Considering PEG of a robotic pursuit of an enemy agent, can we consider the problem as a feedback control problem introducing proportional (P),proportional plus integral (PI) and proportional plus integral plus derivative (PID) laws to improve the performance of the pursuer? The performance can be studied under different bio- inspired pursuit strategies, such as CM, CB and CP. The evader may be allowed to follow reactive and non- reactive control laws. A simpler version of this study for the CM case only has been reported earlier in [7]. Further, in view of the increased agility of the evader (i.e. ability to turn at a lower speed compared to the pursuer), we ask what is the outcome of the PEG given the chance that evader makes a sudden 90 degree turn left or right? This paper is a much expanded version of [8] especially in regard to the sudden turn strategy of the evader.

Bopardikar [9] has shown the Bio- inspired co-operative strategies of pursuer for successful confinement of evader. [9] gives the required number of pursuers and speed ratio for guaranteed confinement strategy. X Liang and Y Xiao [10] show the coalition formation of robots for intrusion detection by using the game theory approach. The paper is based on the nature’s coalition formation such as predator trying to catch the prey. An analytical method is used to study the tradeoff of coalition or collaboration between the robots.

Initial study of camouflage strategies [11,12] are considered when either pursuer or evader is stationary. Srinivasan [13] analyzed and investigated the motion camouflage and highlighted many ways for future extension. The authors of [14] study the unmanned surface vehicles (USVs) for performing patrolling operations and detecting intruders for harbor protection with a view to reducing the number of humans exposed to threat. An intelligent swarm management unit (SMU) is used for the supervision of all the USVs in operation. A real time motion planner for the USVs in the presence of multiple obstacles is also presented.

 [15] addresses the problem associated with the classical pursuit evasion games and mentions that their study is more difficult than the classical one. The author of [15] also explored the geometry of the problem by obtaining sufficient conditions for both pursuer and evader to win. A max- min problem is formulated, from the pursuers point of view, which is solved using outer approximation method. The solution of the max- min formulation is used to synthesize a feedback solution governing the pursuer’s behavior in the form of receding horizon control. [16] discusses a harbor defense situation and the author highlights the important features where the problem is different from the classical PEG.

The main contribution of the paper can be summarized as follows: (i) PI and PID feedback laws are shown to enable the pursuer to capture the evader in a shorter time compared to P alone for different conditions of the evader following non-reactive and reactive control laws. (ii) The PI, PID feedback laws followed by the pursuer enable him to capture the evader and not allow him to escape contrary to the the case of P alone. This is termed tracking performance of the pursuer (iii) In the case the evader uses his agility to turn 90 degree left or right suddenly with respect to the baseline, it is shown that the time to capture the evader can be delayed when the pursuer follows any of the CM, CB and CP strategies. (iv) It is also shown that in certain cases of CB followed by pursuer, with the evader following the sudden turn strategy, the evader is able to totally escape from the pursuer inspite of the speed advantage enjoyed by the pursuer.

The rest of the paper is organized as follows: The following section gives the required background on modeling of PEG and the pursuit manifolds under different strategies. Section 3 presents the feedback control system configuration considered together with the derivation of expressions for PI and PID for the three strategies. Also provided in section 3 is an analysis of the effect of sudden turn of the evader in respect of the CM, CB and CP strategies of the pursuer. Section 4 gives the simulation results together with the discussion on the comparative performance of the different control strategies as well as different control modes of the evader. Section 5 concludes the paper.

2. Background

Wei and Krishnaprasad [17], [18] model the interaction in pursuit in terms of gyroscopically interacting particles. We follow a similar approach.

where   is the position of the pursuer,  its velocity and   is the acceleration of the pursuer. The steering control of the pursuer is given by the scalar u_pr. The  motion of the evader (with speed ʋ) is given by

where  is the position,  is the velocity and  is the acceleration of the evader. The steering control of the evader, , is a scalar. We also define

which is referred to as the ‘baseline’ between the pursuer and the evader.

2.1.  Pursuit manifolds and cost functions

Two particle pursuer evader system is described in the Euclidean plane of two dimensions. We define the cost functions F on the pursuit manifold  G  as F: G × G → associated with different pursuit strategies as in [4] as follows where  represents  the dot product between two unit vectors and   stands for  the Euclidean norm.

to be the cost function associated with classical pursuit.

All three cost functions Γ, Λ and  are well defined and that they take values in the interval [-1,1]. The cost functions Γ, Λ and  define the respective pursuit manifolds. Γ is seen to correspond to the cosine of the angle between r and . Camouflage pursuit manifold is defined by the condition , which corresponds to the case of the angle between r and  being π. (see Figure 1(a)).

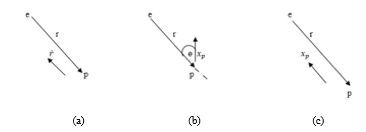Figure. 1 Geometric representation of pursuit manifolds: (a) motion camouflage (CM) pursuit, (b) constant bearing (CB) pursuit and (c) classical pursuit (CP).

      The constant bearing pursuit manifold is represented by the condition . This condition is satisfied when the heading of the pursuer makes an angle  with the baseline vector (as shown in Figure 1(b)). Similarly, the classical pursuit manifold is defined by the condition 1. This condition is satisfied when the heading of the pursuer is aligned (in opposite direction) with the baseline (see Figure 1 (c)).

3. System Modelling

3.1.  Pursuit-Evasion system

Representing

we write (1) and (2) in terms of state equations as follows:

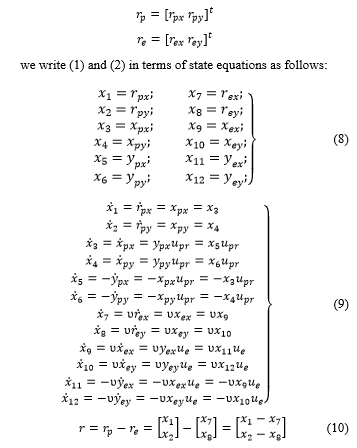
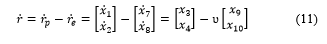3.2.  Feedback Laws.

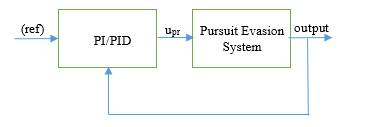
In this sub-section, we formulate the pursuit strategies in terms of feedback control laws. The maintenance of the cost function Γ, Λ and  associated with a strategy at the reference value of  on the respective manifold is represented in the form of a feedback control system as shown in figure 2.  will take expresson for proportional control as , for proportional integral control as  and for proportional, integral and derivative control as .

Figure. 2 Manifold Control

3.2.1. Feedback Laws for CM.

Using the results of [4] the feedback control law is defined as

where  represents  the dot product of  two vectors and  is defined as the vector  rotated counter- clockwise in the plane by an angle . In terms of the system model, (12) can be put as

where  is the proportional (P) setting of the controller.

Proposition 1:

      Using (13) under CM, PI and PID control laws can be derived as

where  is the derivative (D) setting of the controller.

Proof: – see Appendix 1

3.2.2. Feedback Laws for CB.

      Considering CB, the expressions for the control law is given as follows.

Proposition 2:

      For CB the control laws for PI and PID can be expressed as follows.

Proof: – See Appendix 2

3.2.3 Feedback Laws for CP.

Considering CP, the expressions for PI and PID control laws derived under proposition 2 are valid with R= I₂.

3.3 Control law for the Evader.

For the evader the steering control common to (CM, CB and CP of pursuer) can be as follows.

3.3.1 Sudden Turn of evader

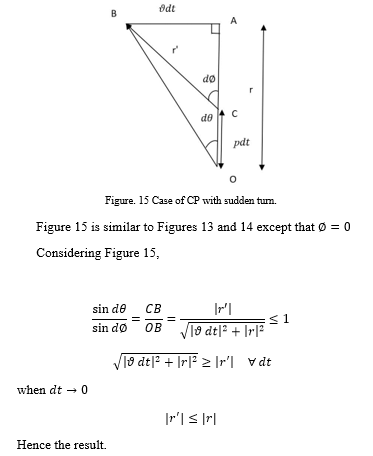
Sudden turn is followed by the evader when the baseline length is shorter than a threshold. The sharp turn is again prevalent in nature where the reduced speed of the evader (victim) compared to that of the predator gives the evader the advantage of agility which enables him to turn sharply trying to escape from the pursuer. The choice of abandoning the other steering laws in favour of the sudden 90-degree turn is taken once the baseline length between the pursuer and evader is perceived to be below a certain threshold. We show below the property that once the evader takes a sudden 90 degree turn with respect to the baseline, he continues to do so in all subsequent moves since the baseline distance between the pursuer and the evader continues to be below the threshold. The property is stated and proved next for the three cases of pursuer strategy, viz, CM, CB and CP.

3.3.1.1 CM

Proposition 3:

Referring the initial baseline between the pursuer and evader as r and after a tangential move for a time , the baseline is denoted as r’. Assuming that the pursuer follows the CM strategy it follows that .

Proof: – See Appendix 3.

Table. 1 Time to reach  and  for different combinations of  for different initial values of  and  for CM.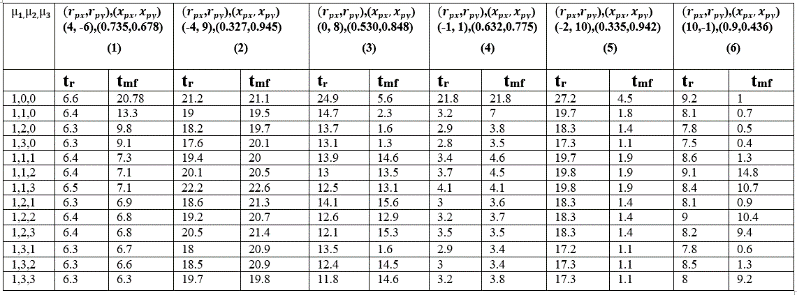

Table. 2 Time to reach  and  for different combinations of  for different initial values of  and  for CB.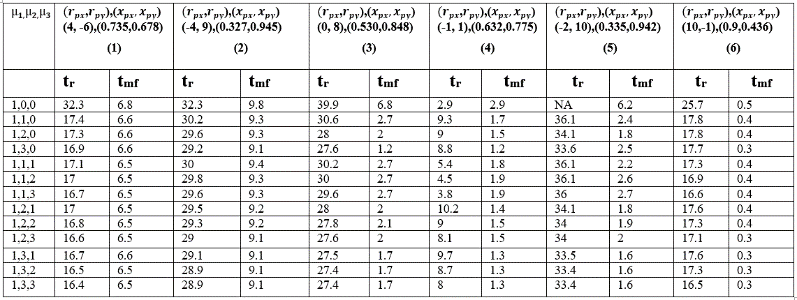

3.3.1.2 CB

Proposition 4:

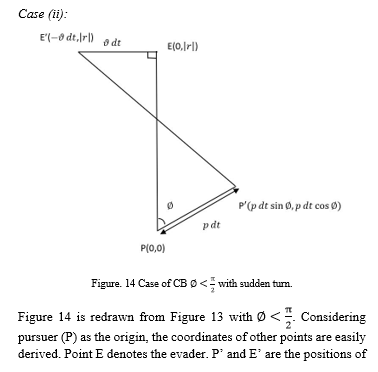
For the case of CB, considering the instantaneous case of sudden turn of 90 degrees left or right by the evader, with the pursuer following the CB law under two cases.

(i) , it follows that

where r and r’ are the baseline vectors initially and after the lapse of an infinitesimal time respectively.

if where  is the instantaneous period of the step considered.  and  are the velocities of the evader and the pursuer respectively.

Table. 3 Time to reach  and  for different combinations of  for different initial values of  and  for CP.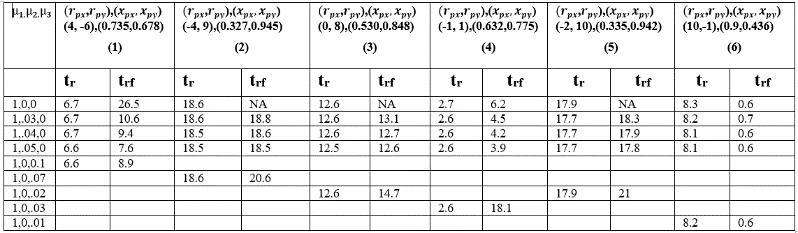

3.3.1.3 CP

Proposition 5:

Assume r and r’ defined as in Proposition 3. When the evader takes a sudden turn left or right 90 degree, with pursuer following CP law case, it can be shown that

Proof: – See Appendix 5.

4. Simulation Results.

4.1.  Time response

4.1.1 Non-reactive case

In this section, we provide the results of simulation of the dynamic equations given in section 3 and discuss the same. We assume  given by (20) corresponds to the non-reactive case of the evader. Tables 1-3 provide results obtained through computer, simulation of the pursuit evasion game for CM, CB and CP strategies respectively under P, PI and PID control. The first columns of Tables 1-3 provide the P, I and D gains used corresponding to  respectively. The next six columns correspond to different initial starting coordinates for  and ,

 and  are assumed to be (0,0)^t and (1,0)^t respectively. The two

sub- columns in Tables 1-3  correspond to time ( ) to reach zero for the magnitude of r and the time ( ) to reach manifold characterized by ,  and  corresponding to CM, CB and CP strategies respectively for the first time. In Table 3, the blank cells correspond to the case of no significant results being obtained in the simulation.

It is seen in Table 1, corresponding to CM, that PI and PID laws tend to improve the performance of the pursuer compared to using P alone, which is the existing method. For example, comparing the rows corresponding to (1, 3, 0) and (1, 3, 3) against (1, 0, 0) in the first column, it is seen that  and  are reduced in the case of PI and PID settings compared to P alone. This holds for all possible starting points considered. Similarly, it is seen in Table 2, corresponding to CB that PI and PID laws tend to improve on the performance of the pursuer compared to using P alone, which can be considered as the existing method. That is,  and  are much reduced in the case of PI and PID settings compared to P alone. This holds for all possible starting points considered. Similarly, it is seen in Table 3, corresponding to CP, that PI and PID laws tend to improve the performance of the pursuer compared to using P alone, which is the existing method. That is,  and  are much reduced in the case of PI and PID settings compared to P alone. This holds for all possible starting points considered.

Table. 4 Time to reach  and  for different combination of  for different initial values of  and  for CM.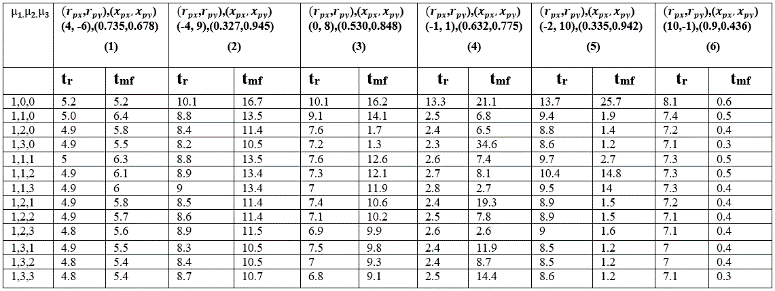

Table. 5 Time to reach  and  for different combination of  for different initial values of  and  for CB.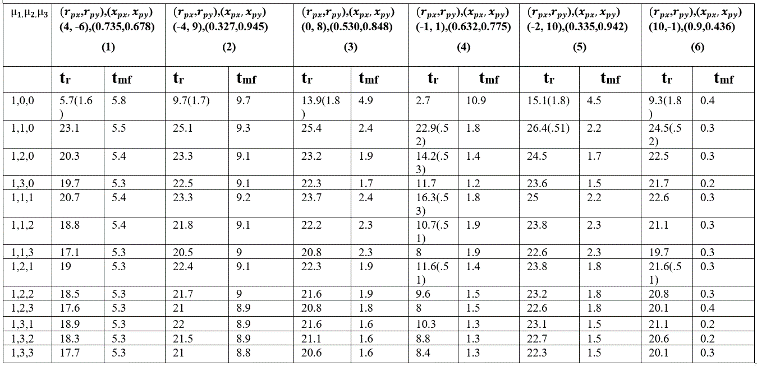

Comparing the performance of CM, CB and CP under feedback laws, the initial condition column (1, 3, 5, 6) in Tables 1-3, show that the CM outperforms followed by CP and CB in terms of shorter . In column 2 in Tables 1-3 the CP outperforms followed by CM and CB in terms of shorter , and in column 4 in Tables 1-3 the CP outperforms followed by CM and CB in terms of shorter . Similarly, in terms of shorter  columns (1-4) in Tables 1-3, CM outperforms followed by CB and CP. For column 5 in Tables 1-3, CB outperforms followed by CM and CP in terms of shorter . For column 6 in Tables 1-3, CB outperforms followed by CP and CB in terms of shorter .

4.1.2 Reactive case

Simulation results of the dynamic equations given in section 3 by using  corresponding to (21) are given below.

It is shown in Tables 4-6, that PI/PID control (proposed) laws correspond to much shorter  and  compared to P alone for the three strategies CM, CB and CP.

Comparison of the different strategies, under feedback laws, shows that in the column (1, 3, 6) in Tables 4-6 CM outperforms followed by CP and CB. In column (2, 4, 5) of Tables 4-6 CP outperforms followed by CM and CB in terms of shorter . Similarly, in terms of shorter  column (1, 4) in Tables 4-6 shows that CB outperforms followed by CM and CP. For column (2, 3) in Tables 4-6, CB outperforms followed by CP and CM in terms of  and . For column (5, 6) in Tables 4-6, CM outperforms followed by CB and CP in terms of   and . The controller setting of D is not included in Table 6 since no significant improvement is seen through simulation using derivative control.

4.1.3 Sudden Turn

Simulation results of the dynamic equations given in section 3 by using  corresponding to (22) are given below.

Tables 7-9 give the data of  and  of CM, CB and CP strategies under sudden turn evader steering control laws. The empty cells in these tables mean insignificant value within the considered time frame. In CM strategies, we can see from Table 4 and Table 7 that by using sudden turn evader control laws,  and  are much delayed (compare the first rows of Table 4 and

Table. 6 Time to reach  and  for different combination of  for different initial values of  and  for CP.

Table 7) from using reactive or non-reactive evader control law for different initial conditions. In case of CB strategy, we can see from Table 5 and Table 8 that by using sudden turn evader control laws, evader escapes from the pursuer for all different initial conditions (compare the first rows of Table 5 and Table 8). This is a very significant result for the evader. For CP strategies, from Table 6 and Table 9, we can see that by using sudden turn evader control laws, capturing of evader is delayed for all initial conditions compared to the case when evader used reactive control law (compare the first rows of Table 6 and Table 9).

Table. 7 Time to reach  and  for P (µ₁) control for different initial values of  and  for CM.

Table. 8 Time to reach  and  for P(µ₁) control for different initial values of  and  for CB.

Table. 9 Time to reach  and  for P(µ₁) control for different initial values of  and  for CP.

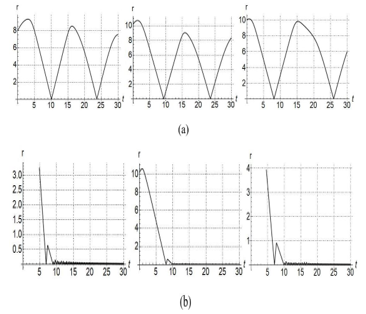Figure. 3  plot for CM using (a) P and (b) PID.

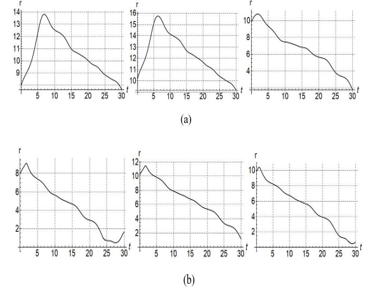Figure. 4   plot for CB using (a) P and (b) PID.

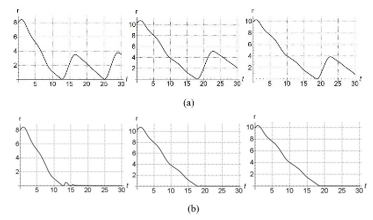Figure. 5  plot for CP using (a) P and (b) PI.

4.2.  Tracking response

Figures 3-4 show the response of the baseline magnitude  as function of time for different initial settings. When |r| becomes zero, it means the distance between pursuer and evader is zero, and hence the evader is captured. Figure 3(a) and Figure 4(a) correspond to P control while Figure 3(b) and Figure 4(b) corresponds to PID control. Similarly, for Figure 5(a) and Figure 5(b) correspond to P and PI respectively for different initial conditions. It is clearly seen from Figures 3-5 that tracking response of the zero line of the baseline magnitude (i.e. the zero line of the distance between the pursuer and evader) is clearly superior for PID/ PI control, compared to P alone (top rows in Figures 3-5). In fact, P alone is not able to track the zero-baseline magnitude at all. Note that the magnitude of baseline vector going to zero corresponds to evader being captured.

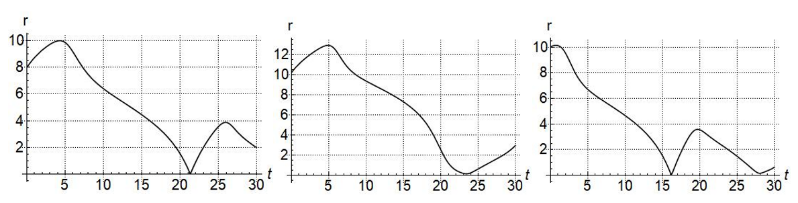Figure. 6  plot for CM using sudden turn evader steering law.

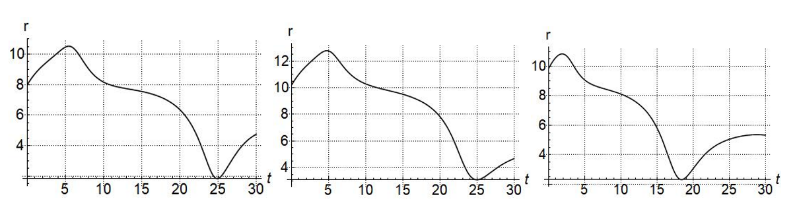Figure. 7  plot for CB using sudden turn evader steering law.

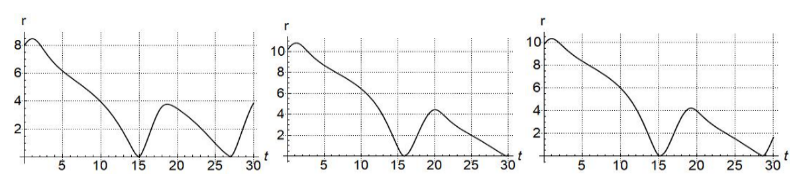Figure. 8  plot for CP using sudden turn evader steering law.

Figures 6-8 show the response of the baseline magnitude  as function of time for different initial settings for CM, CB and CP strategies respectively. In Figure 6(a) represents the initial starting position of pursuer given as (0, 8) in x- y co-ordinate. 6(b) and 6(c) correspond to starting positions of (-2, 10) and (-4, 9) respectively. For the sake of comparison, (a), (b) and (c) in Figures 7 and 8 also correspond to the same respective starting positions. It is clearly seen from Figures 6-8 that the time to capture the evader by the pursuer is much delayed by using the sudden turn strategy compared to the case when evader used the reactive and non-reactive steering control laws. This can be seen by comparing Figure 3(a) with Figure 6, Figure 4(a) with Figure 7 and Figure 5(a) with Figure 8. In fact in Figure 4,  never reaches zero meaning that the evader is never captured in that case.

4.3.  Trajectories of pursuer and evader.

We consider in this section, the actual trajectories followed by evader and pursuer.

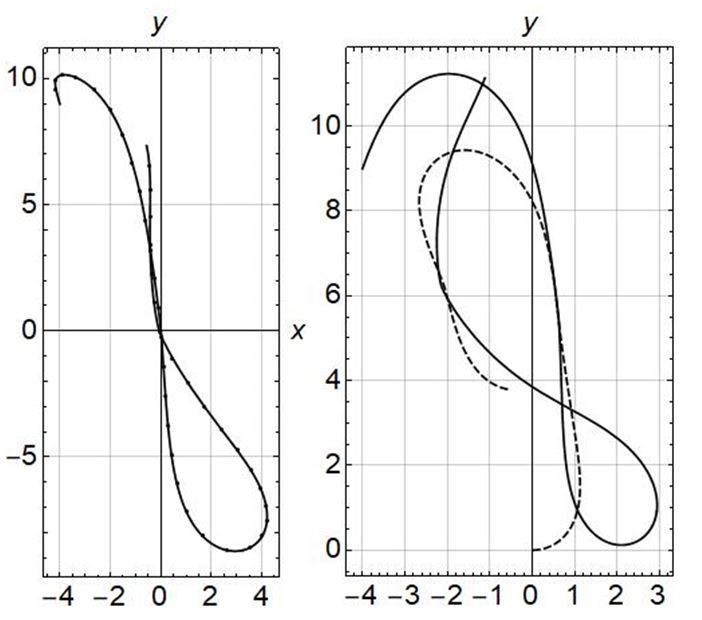Figure. 9 For normal pursuer capture evader, (a) magnitude of r, (b) trajectories of pursuer (solid line) and evader (dashed line).

Figure 9 shows evader being captured in a certain time by the pursuer. Figure 9(a) shows the magnitude of r. Figure 9(b) shows the trajectories of pursuer and evader for a 30 sec timeline. The starting point of evader is (0, 0) in x-y coordinate and the starting point for the pursuer is (-4, 9). Figure 10 shows the case when the evader escapes from the pursuer. This happens only in the case of

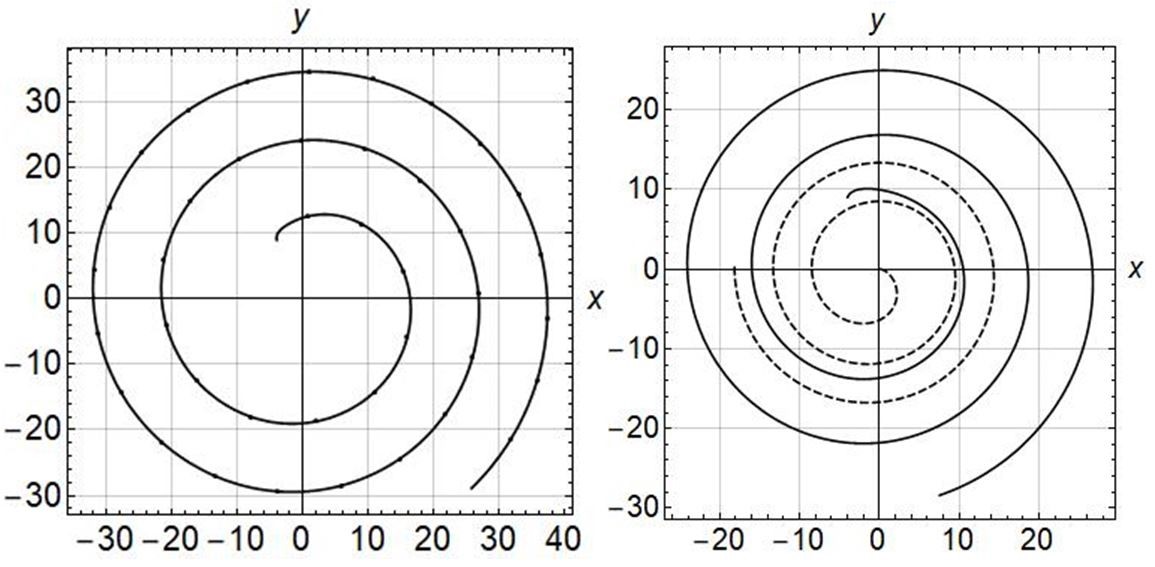Figure. 10 For the case evader escapes from pursuer, (a) magnitude of r, (b) trajectories of pursuer (solid line) and evader (dashed line).

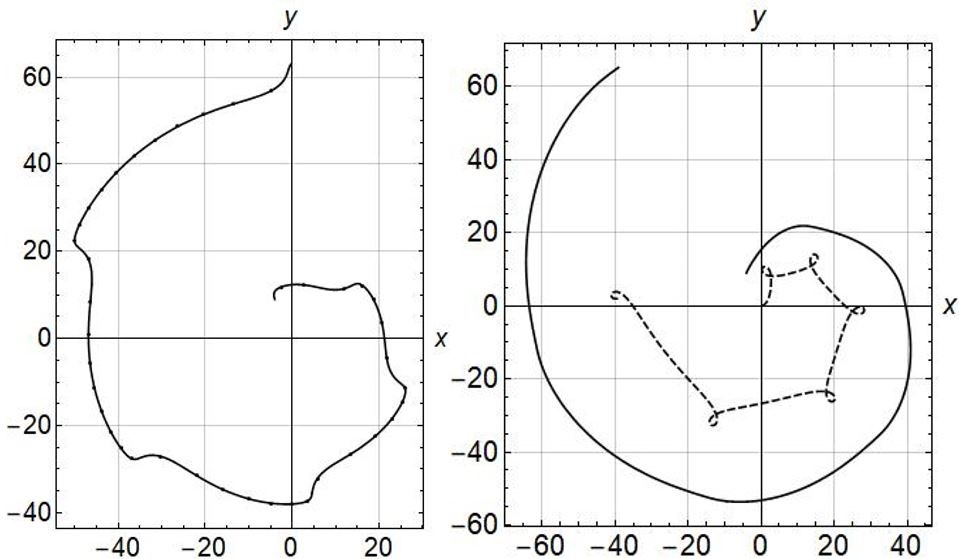Figure. 11 For , (a) magnitude of r, (b) trajectories of pursuer (solid line) and evader (dashed line).

CB strategies when evader suddenly turn 90 degree left or right as discussed in Proposition 4 case (i). So, in Figure 10 (a) the value of r keeps on increasing. Figure 10 (b) shows  the trajectories of pursuer and evader in 30 sec timeline. Figure 11 is for the case when  and the baseline distance between the pursuer and the evader tend to reach a constant value.

5. Conclusions

Pursuit evasion game (PEG) has been studied in the literatiure using geometric control theory. Control laws for the pursuer have been derived so as to make the pursuer follow a certain manifold according to the different bio-inspired strategies used. The performance of the pursuer control laws is specified in terms of  time to capture the evader and tarcking of pursuer path on the manifold given certain fixed evader escape strategies Though the existing pursuer control laws are optimal, it is shown in the paper,  through simulations, that adding integral and derivative actions to the pursuer control laws tends to improve the performance of the pursuer further independent of the strategy used. Towards that, the pursuer path tracking on the manifold is specified in terms of a feedback loop with the reference being the cost function of the manifold used. The proportional (P), proportional- integral (PI) and proportional- integral- derivative (PID) control laws are studied on the loop with the existing control law being considered as proportional law.  Due to the noninear nature of control laws in a vector setting the derivation of PI and PID control laws are non-trivial.To mimic the nature further, a sudden turn strategy is assumed to be employed by the evader in view of evader’s agility advantage while moving at a lower speed compared to the pusuer. The dynamics of the PEG with the sudden turn strategy of the evader has been studied through a theoretical analysis supported by simulation. It is shown that the sudden turn strategy can help the evader delay the capture by the pursuer and in a certain case the evader can even totally excape from the pursuer. As a future work, one could consider the case when the evader moves at a varying speed (instead of the constant speed assumed in the paper) as in commonly seen in nature.

Appendix 1:

Proof of Proposition 1

P and PI control:

are the control output of P and PI controller derived as given in the proposition in a straightforward way.

PID Control output u_pid  can be derived as follows.

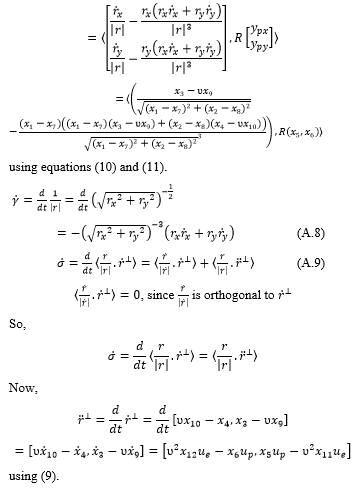
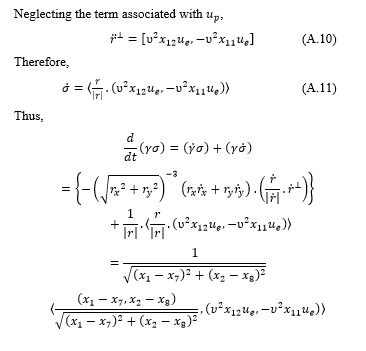
Appendix 3:

Proof of proposition 3:

Referring to Figure 12, r is the initial baseline while r’ is the baseline in the next step after a lapse of time . p and  are the velocities of the pursuer and the evader respectively. The sudden turn with respect to the baseline at every move result in a motion by the evader in a tangential direction resulting in describing the arc ‘ab’ in Figure 12 by the evader for arbitrarily small . We then have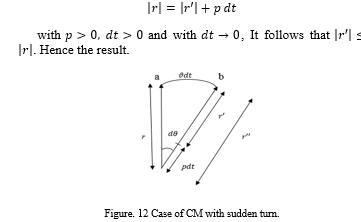

1. P. Svec, A. Thakur, B. C. Shah, and S. K. Gupta, “USV Trajectory Planning for Time Varying Motion Goals in an Environment with obstacles,” Terpconnect.Umd.Edu, pp. 1–11, 2012.
2. R. Issacs, “Differential Games,” New York: Wiley, 1965.
3. E. Wei, E. W. Justh, and P. S. Krishnaprasad, “Pursuit and an evolutionary game,” Proc. R. Soc. A Math. Phys. Eng. Sci., vol. 465, no. 2105, pp. 1539–1559, 2009.
4. D. Pais and N. Leonard, “Pursuit and Evasion: Evolutionary Dynamics and Collective Motion,” AIAA Guid. Navig. Control Conf., pp. 1–14, 2010.
5. W. Li, “A Dynamics Perspective of Pursuit-Evasion: Capturing and Escaping When the Pursuer Runs Faster Than the Agile Evader,” IEEE Trans. Automat. Contr., vol. 62, no. 1, pp. 451–457, Jan. 2017.
6. W. Li, “Escape Analysis on the Confinement-Escape Problem of a Defender Against an Evader Escaping from a Circular Region,” IEEE Trans. Cybern., vol. 46, no. 9, pp. 2166–2172, 2016.
7. L. Obiroy Singh and R. Devanathan, “Performance improvement of bio-inspired strategies through feedback laws,” in Advances in Intelligent Systems and Computing, 2018, pp. 143–156.
8. L. Obiroy Singh and R. Devanathan, “Comparative Study of the Performance of Application of Bio-Inspired Strategies to Pursuit Evasion Game Under Feedback Laws,” in The 18th International Conference on Control, Automation and Systems,South Korea, 2018, pp. 276–281.
9. J. H. S.D Bopardikar, F Bullo, “A Cooperative Homicidal Chauffeur Game,” Automatica, vol. 45, pp. 1771–1777, 2009.
10.  X. Liang and Y. Xiao, “Studying Bio-Inspired Coalition Formation of Robots for Detecting Intrusion Using Game Theory,” IEEE Trans. Syst. Man Cybern., vol. 40, no. 3, pp. 683–693, 2010.
11.  H. . Cott, “Adaptive Coloration in animals,” London: Methues, pp. 141–143, 1966.
12.  K. . Roeder, “Nerve Cells and insect behaviour,” Cambridge, MassachusettsHarvard Univ. Press, pp. 160–164, 1967.
13. M. V Srinivasan and M. Davey, “Strategies for Active Camouflage of Motion,” in Biological Sciences, pp. 19–25.
14. E. Simetti, A. Turetta, G. Casalino, E. Storti, and M. Cresta, “Protecting Assets within a Civilian Harbour through the use of a Team of USVs: Interception of Possible Menaces,” in IARP workshop on robots for risky interventions and environmental surveillance maintenance (RISE’10), 2010.
15.  J. Walrand, E. Polak, and H. Chung, “Harbor Attack: A Pursuit- Evasion Game,” in Forty- Ninth Annual Allerton Conference, 2011, pp. 1584–1591.
16. S. Lee, E. Polak, and J. Walrand, “A receding horizon control law for harbor defense,” in 51st Annual Allerton Conference on Communication, Control and Computing, 2013, pp. 70–77.
17.  E. W. Justh and P. S. Krishnaprasad, “Steering laws for motion camouflage,” Proc. R. Soc. A Math. Phys. Eng. Sci., vol. 462, no. 2076, pp. 3629–3643, 2006.
18.  E. W. Justh and P. S. Krishnaprasad, “Natural frames and interacting particles in three dimensions,” Proc. 44th IEEE Conf. Decis. Control. Eur. Control Conf. CDC-ECC ’05, vol. 2005, pp. 2841–2846, 2005.

(Click Here)

(Click Here)