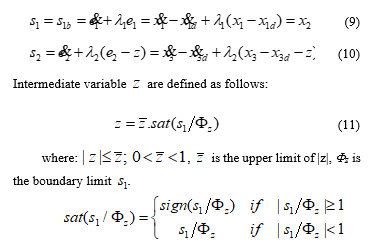An Adaptive Fuzzy-Sliding Mode Controller for The Bridge Crane
Adv. Sci. Technol. Eng. Syst. J. 4(3), 164–170 (2019);
DOI: 10.25046/aj040322
This article presents a bridge crane nonlinear dynamic model in 2-dimensional space, and then given a novel adaptive fuzzy-sliding mode controller based on combining sliding mode control with fuzzy logic and Lyapunov function. Firstly, the article proposes an intermediate variable to link signal between two slide surfaces, related to trolley movement and payload swing. Then the fuzzy controller, compensative controller and parameter adaptive update law for the bridge crane are defined. The asymptotic stability of the proposed bridge crane control system is proven based on Lyapunov stability theory. Simulation results show that the adaptive fuzzy-sliding mode controller ensures the trolley follows the input reference with the short settling time, eliminating steady error, and anti- payload swing, anti-disturbance.
1. Introduction
The bridge crane is a lifting machinery which commonly used in industry and transportation to move goods from one location to another. The bridge crane consists of three main components: hoist, trolley and beam, corresponding to three movements: lifting and lowering the cargo of the hoist (mounted on the trolley), horizontal movement of the trolley (on the beam), and vertical movement of the beam (on the factory frame). Goods (refer to as payload) are linked to cargo hoist by the cable and hanger. This connection causes the vibration of the payload when the crane moves. This is undesirable – causing unsafe operation of the crane, reducing the accuracy in controlling the cargo transport of crane, reducing the crane operation.
In some cases of actual crane operation, it is often focused on controlling the exact position of the trolley, after lifting the payload. In this case, the bridge crane is studied as a trolley movement in the 2D space, created by the horizontal movement of the trolley and the verticality of the cable. Common works on position control of the trolley are often based on state feedback control, PID control [1, 2], LQR control [3], PID combined with fuzzy [4-7], PID adjusting parameters [8] and obtain certain results. In [1], the state feedback controller is combined with the integral part to eliminate the steady error. The work [4] presents a controller PID combined with the fuzzy-sliding mode control. These controllers are designed based on the linear model of the crane and the existing of payload oscillation.
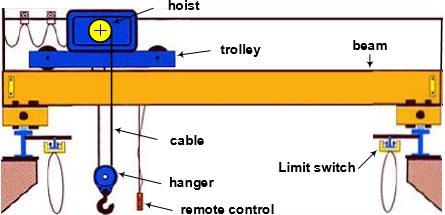Figure 1. Bridge crane movement in 3D: trolley-0x, beam-0y, hoist-0z.
In recent times, the researches have taken into account the nonlinearity of the crane based on back stepping [9], nonlinear control [10, 11], sliding mode control [12], sliding mode control combined with fuzzy logic [13], partial linear feedback control [14], sliding mode control combined with partial linear feedback [15], sliding mode control combined with adaptive fuzzy control [16], or neural network [17]. These controllers have enriched the crane control strategy, ensuring that trolley follows the reference trajectory with small static error and small payload oscillation. However, these control algorithms are quite complicated, require a large amount of computation, the deployment of them on hardware devices is difficult and not considering the impact of noise in the working environment of the crane, such as the impact of the wind.
This article presents a nonlinear mathematical model of a crane in two-dimensional space (2D bridge crane model). On that basis, an adaptive fuzzy-sliding mode controller is designed for 2D crane model based on the sliding mode control principle combined with fuzzy logic and Lyapunov function, ensuring that the trolley moves quickly, following set reference and eliminating payload oscillation, anti-disturbance. The rest of this article is organized as follows. Section 2 introduces the bridge crane dynamic model. Section 3 deals with the design of controllers for the bridge crane 2D. Section 4 presents the simulation results. Finally, section 5 presents conclusions.
2. Bride crane dynamic model
The motion of the bridge crane in the two-dimensional space Oxz as shown in Figure 2, where: x(t) is the position of the trolley moving in the Ox direction, α(t) is the oscillation angle of the payload. Assuming that the cable is a rigid rod and connected with a cargo hanger, the cable length is constant and the cable mass is negligible; ignore the trolley friction when moving; consider payload as the point P(xp,zp) with mass mp; trolley with mass mt; Fx is the force driving a trolley in the Ox-direction, g is the gravitational acceleration.
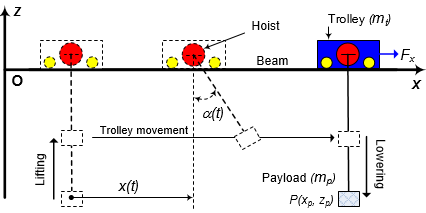Figure 2. Bridge crane trolley movement in 2D
The dynamic model of bridge crane is defined based on energy conservation law. The total kinetic energy K and the potential energy T of the system are determined as follows:
After transforming, we obtain the mathematical equation describing the dynamics of crane:
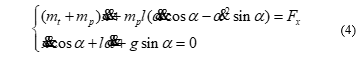The system of equations (4) is separated into 2 subsystems, describing 2D bridge crane dynamics in the state space, including: system A describes the trolley movement; system B describes the payload oscillation.
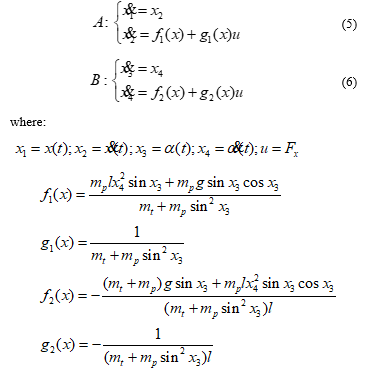The 2D bridge crane model is a nonlinear system. When the trolley moves, the payload oscillation will appear, so that as the proposed controller not only ensures the trolley follows the reference trajectory but also quenching payload oscillation, in order to ensure safe operation and accurate cargo transportation.
3. Adaptive fuzzy-sliding mode controller design for the bridge crane
3.1. Sliding mode controller
In this research, mathematical model of 2D bridge crane is described by equations (5) and (6), corresponding to system A, system B.
The goal here is to synthesize a controller so that the outputs of the crane (5) and (6) follows on the input reference i.e. the steady error:
According to the sliding control principle, we determine the general sliding surface for systems A and B:
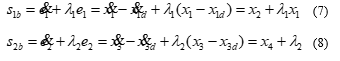where: are positive constants.
To ensure the control target for bridge crane (5) and (6), we define the sliding surface for system A to ensure precise control of trolley position and sliding surface for system B to ensure the general control target for bridge crane, that is: controlling the trajectory of the trolley, quenching the payload oscillation of the payload, the anti-disturbance. Therefore, we need to use the intermediate variable to link the signal between the sliding surface and the sliding surface On that basis, the author defines the sliding surface as follows:
where: , is the upper limit of |z|, Fz is the boundary limit
Because of it can be effective in reducing. When reduced is also decreases. When then and achieves the control target for crane (5) and (6). Therefore, by adding intermediate variables now and at the same time tends to 0.
According to the sliding control principle, when we get the sliding control law for bridge crane, it looks like this:
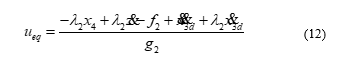Control law (12) for bridge crane is a complex nonlinear function, for which is not defined. Therefore, in this article, the author proposes adaptive fuzzy-sliding mode control law to imitate the sliding control law (12) based on fuzzy logic control and Lyapunov function.
3.2. Fuzzy controller based on sliding mode control principle
Define fuzzy controller with input and output with fuzzy control rules i-th as below:
where: Mq, Ms2 are the appropriate values when designing.
The control signal (16) is closest to (12), in other words, the deviation d(t) is the smallest:
Here the limit D is a positive number, but it is uncertain in practice. Called the estimated value of the limit D. Then the estimate of the limit D is is defined as follows:
Therefore, based on (12), the author proposed a new control law for bridge cranes (5) and (6) with the following form:
Here the fuzzy controller (14) has the closest value to (12); and is the compensated controller to compensate for the deviation (if any) between control laws (14) and (12). The compensation controller is determined based on the Lyapunov stability theory, ensuring the stable asymptotic bridge crane control system.
3.3. Adaptive laws based on Lyapunov function
Next, the author summarizes the compensation controller and determines the adaptive law to update the parameters , so that (19) optimal operation is closest to (12), which means and . Set and select Lyapynov function with the following form:
According to Lyapunov stability theory, the bridge crane control system is stable, the necessary condition is . From there according to (22), we determine the compensation controller according to (23) and the parameter update law according to (24), the parameter update law as follows (25).
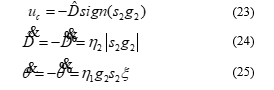3.4. Prove asymptotic stability of bridge crane control system
Replacing (23,24,25) into (22) we obtain:
According to (24), Lyapunov (20) function, , which ensures that is limited. Thus, when time reaches infinity function V goes to 0:
This also ensures that when then , i.e. the crane control systems (5) and (6) are asymptotically stable, the output is tracked to the input reference.
Thus, the crane control system described by (5) and (6) uses the new control law proposed in the article, determined by (19), (14), (23), (24), (25) based on combination of sliding mode control, fuzzy logic and adaptive law based on Lyapunov function, ensuring precise control of the trolley position according to the set reference with eliminated payload oscillation, anti-disturbance.
The block diagram of adaptive fuzzy-sliding control system for 2D crane is shown as Figure 3, including: sliding surface block, fuzzy control block and compensation control block, parameters adaptive update block.
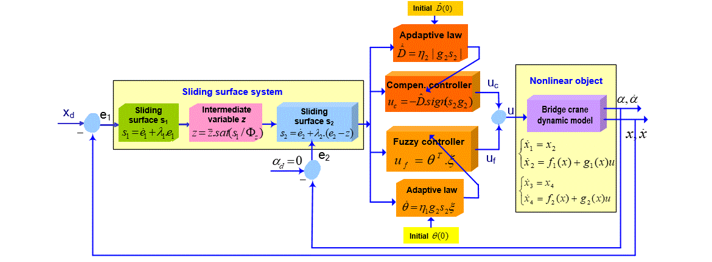Figure 3. The block diagram of adaptive fuzzy-sliding control system for 2D crane
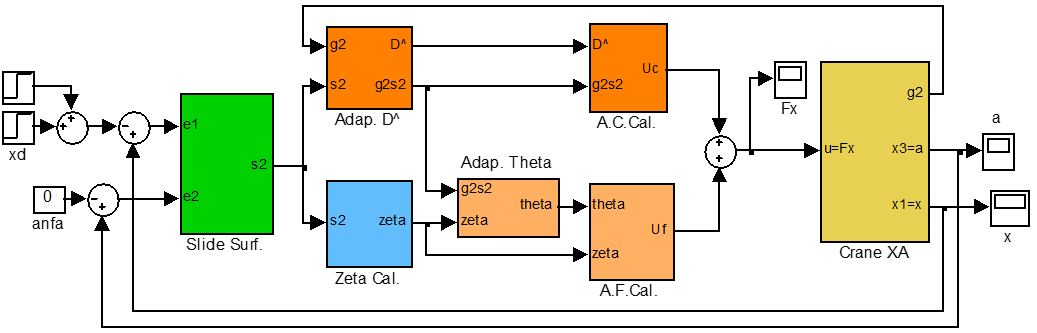Figure 4. Simulation diagram of the bridge crane adaptive fuzzy-sliding mode control system
4. Simulation results
Simulation parameters of the crane are selected based on physical crane model at UTC laboratory [1].
According to the principle of sliding mode control [12] and crane parameters [1], we choose the sliding surface parameters as follows:
Building a 2D crane control system on Matlab, using the adaptive fuzzy-sliding control law (AFS) proposed in the paper, we obtained the simulated system diagram as shown in Figure 4, including function blocks: Slide Surf block: calculate the sliding surface of the system; ZetaCal block: calculate ; Adap D^ block: calculate the update value for the offset compensation controller; Adap. Theta block: calculate updated value for fuzzy controller; AF Cal. block: output of fuzzy controller; AC Cal. block: the output of the controller compensates for deviation; Crane XA block for bridge crane dynamic model.
Based on experience in crane operation and fuzzy control principle, with the above crane parameter [5], the author performs fuzzy input s2 of the controller (14) by {NB, NM, NS, ZE, PS, PM, PB} having triangular integrated functions with domain s2 Î[-20; +20] and fuzzy output uf with {UN, UM, US, UZ, FS, FM, FB} having singleton functions with the physical value domain uf Î[0;100].
Simulation scenario of the bridge crane adaptive fuzzy-sliding control system includes the following cases:
+ Case 1: Let the trolley run to position 0.5m and then the trolley runs to position 1.0m and changes coefficients l1, l2;
+ Case 2: Let the trolley run to position 0.5m and then the trolley runs to position 1.0m and changes coefficients h1, h2;
+ Case 3: Let the trolley run to position 0.5m and then the trolley runs to position 1.0m and changes coefficients ;
+ Case 4: The input reference is a slope;
+ Case 5: There is impact disturbance;
+ Case 6: Use AFS controller and PID controller [1].
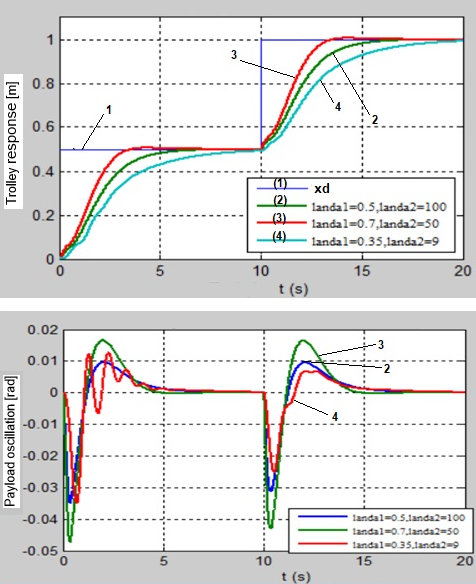Figure 5. Crane response with different
Table 1. The proposed controllers’ performance
| Controller
Index |
PID | AFS |
| Rise time | Small, ~2.5s | Small, ~2.5s |
| Over shoot | Large, 20.5% | Not |
| Steady time | Large, ~7s | Small, ~5s |
| Steady error | <5%, but large with disturbance | ~0, or very small |
| Anti-swing payload | <10o, but large with disturbance | ~0, or very small |
| Anti-disturbance | <10o, but large with loud disturbance | ~0, or very small |
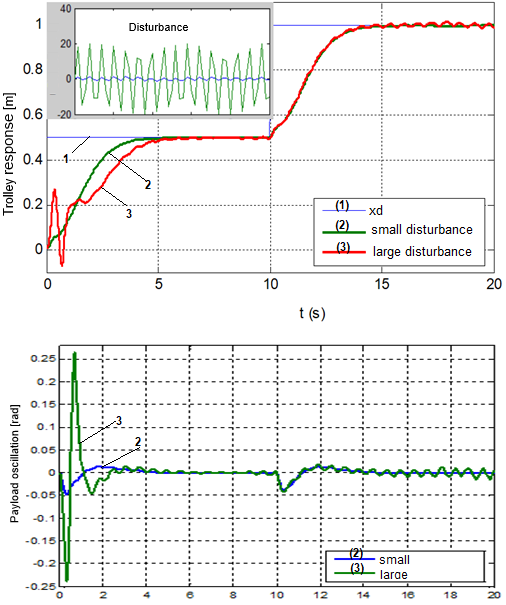Figure 6. Crane response as affected by disturbance
Simulation results show that the quality of the bridge crane control system as using AFS controller is better than as using PID controller. The application of the AFS controller to the crane obtained the following results: quick trolley’s position response, short settling time, eliminating steady error, anti-swing (or very small) payload, anti-disturbances (or very small).
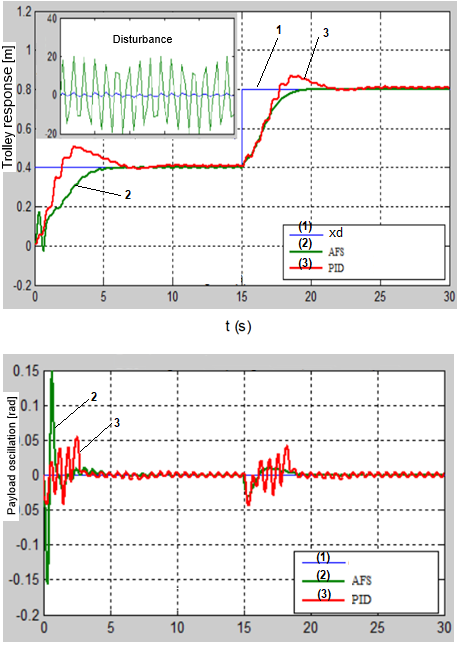Figure 7. Crane response with AFS and PID controller
The simulation results also show that the selection of the coefficient of the sliding surface affects the quality of the adaptive control system of fuzzy-sliding crane, specifically as follows: when increasing , the trolley position response is better but greater is the payload oscillation; when decreasing or increasing it too large, the payload swings strongly; when is too small or when is too large, the trolley position response has vibration and greater payload oscillation; when decreases or decreases too small, the trolley position response has vibration and the payload Will swing larger.
5. Conclusion
The article has proposed a new adaptive fuzzy-sliding mode controller (AFS) for 2D bridge crane based on combining sliding mode control with fuzzy logic and Lyapunov function. The AFS controller ensures the objective of controlling the position of the trolley tracking according to the reference trajectory, eliminating the payload oscillation and anti-disturbance (small amplitude). The quality of the bridge crane AFS control system is better than PID controller when crane is affected by large disturbance. The adaptive fuzzy-sliding mode control algorithm allows simple installation on hardware control devices with a normal amount of calculation. The AFS controller allows the crane to operate safely and reliably in harsh environments, such as the harbor.
The success of the AFS controller for 2D bridge crane will continuously study to be applied for the object in real time and for 3D crane with the random disturbances.
Conflict of interest
The authors declare no conflict of interest.
- Trinh Luong Mien, Nguyen Van Tiem, Design the state feedback controller for bridge crane, The 5th national metrology conference, 20-21/05/2010, 720-725, 2010.
- Khalid L. Sorensen, William Singhose, A controller enabling precise positioning and sway reduction in bridge and gantry cranes, Control Engineering Practice 15, 2007.
- Jafari J., Ghazal M., Nazemizadeh M., A LQR Optimal Method to Control the Position of an Overhead Crane, International Journal of Robotics and Automation, 2014.
- Le Xuan Hai, Thai Huu Nguyen, et al., Anti-sway tracking control of overhead crane system based on pid and fuzzy sliding mode control, Journal of Science and Technology 55(1), 116-127, 2017.
- Amanpreet Kaur, Priyahansha, Shashiprabha Kumari, Tanvi Singh, Position Control of Overhead Cranes Using fuzzy Controller, International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering, 2014.
- Pal A.K., Mudi R.K., An Adaptive PD-Type FLC and Its Real Time Implementation to Overhead Crane Control, International Association of Scientific Innovation and Research, 2013.
- Shebel Asad, Maazouz Salahat, Design of Fuzzy PD-Controlled Overhead Crane System with Anti-Swing Compensation, S. ASAD ET AL Engineering, 2011.
- Nazemizadeh, A PID Tuning Method for Tracking Control of an Underactuated Gantry Crane, Universal Journal of Engineering Mechanics, 2013.
- Yonggang Li, Shuqing Zhou, Hongqiu Zhu, A backstepping controller design for underactuated crane system, The 30th Chinese Control and Decision Conference (2018 CCDC), 2018.
- Mahan Mahrueyan and Hamid Khaloozadeh, Designing a Nonlinear Optimal Anti-Sway Controller for Container Crane Systems, International Conference on Circuits, System and Simulation, 2011.
- Fang Y., Zergeroglu E., Nonlinear coupling control laws for overhead crane system, IEEE/ASME Transaction on Mechatronics, 2003.
- Shibly Ahmed AL-Samarraie, Bashar Fateh Midhat, Sliding Mode Controller Design for a Crane Container System, IJCCCE, 2014.
- Diantong Liu, Jianqiang Yi, Dongbin Zhao, Wei Wang, Adaptive sliding mode fuzzy control for a two-dimensional overhead crane, Mechatronics 15, 2005.
- Hahn Park, Dongkyoung Chwa, and Keum-Shik Hong, A Feedback Linearization Control of Container Cranes: varying rope length, International Journal of Control Automation and Systems, 2007.
- Tuan Anh Le, Soon-Geul Lee, Sang-Chan Moon, Partial feedback linearization and sliding mode techniques for 2D crane control, Transactions of the Institute of Measurement and Control 2014, Vol. 36(1) 78–87, 2014.
- Trinh Luong Mien, Adaptive fuzzy sliding mode control for gantry crane as varying rope length, International Journal of Engineering and Technology, Vol. 8 No. 4 Aug-Sep2016, 1784-1791, 2016.
- Chen Zhi-mei, Meng Wen-jun, Zhang Jing-gang, Intelligent NN anti-swing control for bridge crane, J. Cent. South Univ., 2012.