1. Introduction

This paper is extension of the work originally presented in 2018 IEEE International Topical Meeting on Microwave Photonics (MWP) titled “Experimental evaluation of digital predistortion for VCSEL-SSMF-based Radio-over-Fiber link” [1]. The fifth generation (5G) technology is envisaged to provide faster internet access with low latency, cost effectiveness and pervasive mobile coverage [2-3]. Radio over Fiber (RoF) is a pertinent technology to deal with exorbitant requirement of bandwidth multivariate wireless services both for outdoor and indoor scenarios [4-6], and is regarded as a significant technology for the next generation networks [7].

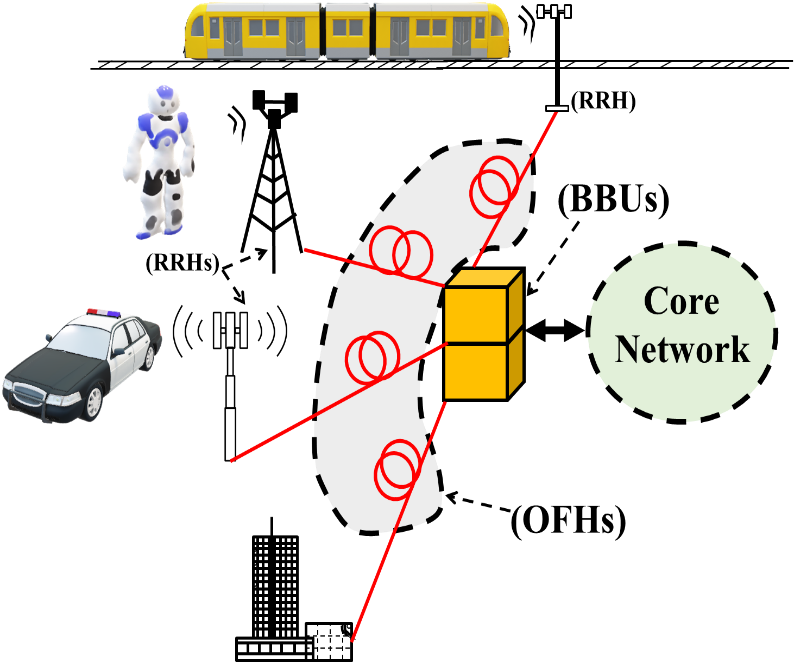Figure 1: Basic C-RAN architecture showing optical fronthauls (OFHs)

In particular, RoF technology can provide an essential platform for building centralized/cloud radio access network (C-RAN) which should be able to control the centralized base band units (BBU) coming from different base stations and remote radio heads (RRHs) [8].

 The interconnectivity of these BBUs with RRHs is economically viable with the distribution network known as the ‘fronthaul’ [9-10]. The RoF technology is then a suitable candidate for the fronthauling due to its inherent capillary properties. Figure 1 shows the C-RAN utilizing optical fronthauls (OFHs).

Within these short-medium reach networks, OFHs based on the RoF technology can be realized utilizing Standard Single mode Fiber (SSMF) or also Multimode Fiber (MMF) [11]. In both cases, a possible solution which keeps low levels cost and power consumption can be obtained utilizing Vertical Cavity Surface Emitting Lasers also known as VCSELs which emit in the first optical window (wavelength l=850 nm) as the optical source.

While the use of VCSELs operating at short wavelengths is a relatively consolidated choice finding application e.g. in combinations with Plastic Optical Fibers within in-building networks [12-13] or in combination with MMFs within data centers [14], care must be taken in front of the possible impairments due to the multimodal behavior of SSMFs that operate at the 850 nm [15]. The presence of  multimodal behavior would  indeed be absent if  expensive VCSELs operating at 1.3  and 1.55  were utilized , in which the major SSMF-related impairments could just be ascribed to optical nonlinear effects and/or to chromatic dispersion [16-17]. However, appropriate countermeasures have been proposed, which can prevent this last impairment cause to be critical [18-19].

Besides the cited OFH, VCSEL-based RoF systems can be found in multivariate scenarios, being utilized for radio astronomic signal transmission [20], multi service indoor wireless signal distribution [21], or machine learning detection [22].

In all these cases, a cardinal issue is represented by the impairments of the opto-electronic devices and particularly the whole VCSEL based Radio over Fiber system. Such nonlinearities, that arise due to relatively stable causes like nonlinear attributes coming from laser diode and perhaps from photodiode [23]. These nonlinearities can also arise due to little dynamics of VCSELs [24], e.g., when high Peak-to-Average Power Ratio (PAPR) signals are transmitted and can have an important role especially for multi-channel transmission. They indeed can cause high in and out of band distortion, which leads to higher interference among near channels.

In order to minimize the nonlinearities in RoF transmission, different methodologies have been proposed that comprises of digital and analog electrical techniques [25-27]. Among them, Digital Predistortion (DPD) has been regarded to be effectual method that leads to reduction in nonlinearities of  RoF systems. The primary intension behind this method exploits a digital predistorter (PD) which has inverse and nonlinear profile as that of the Radio over Fiber system. Consequently, when cascaded with the RoF system, it will lead to linearization of the overall cascaded system. DPD linearization technique using memory polynomials based on Volterra series has been applied to Non linear RoF link [26-28]. Similarly, the Digital Predistortion technique based on canonical piecewise-linear (CPWL)  function was proposed for intensity modulated/direct detection RoF system [29].  All the aforementioned techniques apply the distortion compensation considering the RoF systems as “black box”.

In our previous work reported in [1,30], we demonstrated the novel implementation of DPD implied to considered radio over fiber link which was based on single mode (SM) based VCSEL for LTE applications utilizing Memory Polynomial (MP) architecture. The highlighted results were obtained in back-to-back (B2B) configuration, i.e. utilizing a SSMF fiber patch-cord of a few meters length.

In this paper, the novelty of the current work is summarized as follows: (1) for the first time, the evaluation that was performed in [1] is extended by considering the same SM VCSEL-based RoF system, not in B2B configuration, but equipped with SSMF spans of different lengths; (2) Moreover, also Multimode (MM) VCSEL-based RoF systems are analyzed, utilizing different lengths of MMFs, (3) in addition, to the DPD technique based on Memory Polynomials (MP) utilized in [1], another architecture named as Generalized Memory Polynomial (GMP), is utilized as well, which in general shows an improved effectiveness with respect to MP; (4) the DPD is trained and tested near to threshold to check the efficacy of the proposed technique.

As a performance index evaluation, the link linearity improvements are observed by calculating the Adjacent Channel Power Ratio (ACPR), Normalized Mean Square Error (NMSE), spectral regrowth, Normalized Magnitude (AM/AM) and Normalized phase (AM/PM).  The paper is arranged as follows. In Section 2, modeling methodology is highlighted while Section 3 outlines the predistortion learning architecture. Section 4 discusses the estimation algorithm while Section 5 explains briefly the characterization and experimental setup. Section 6 presents the results in detail. Finally, conclusions are drawn in Section 7.

2. Modeling Methodology

The architecture of the predistortion technique is shown in Figure 2 which utilizes Indirect Learning Architecture for the estimation of PD training coefficients [31-34]. Since the statistic of the waveform will remain the same over time, therefore, it can be assumed that system nonlinearity is not time varying and the training of the predistortion can be applied in an off-line practice. This will not only reduce the expenditures and over heads of the predistorter but also avoids the need of an identification algorithm. The identification of DPD is performed in one step. Hence, a linear estimation of PD coefficients result in  straightforward identification.

At first, the training phase calculates the predistorter coefficients. At this point, the RoF system output , becomes input to the Pre-Distorter Training block which is defined as    where  denotes the gain of the system. The coefficients appraisal can be made using least-squares-based algorithm and is described in Sec. 3. The convergence point of the training is achieved by minimizing the error function. Eventually, the computed training coefficients are employed to the predistorter referred as Digital Pre-Distorter in Figure 2. The predistorter models utilized are derived from the classical Volterra series.

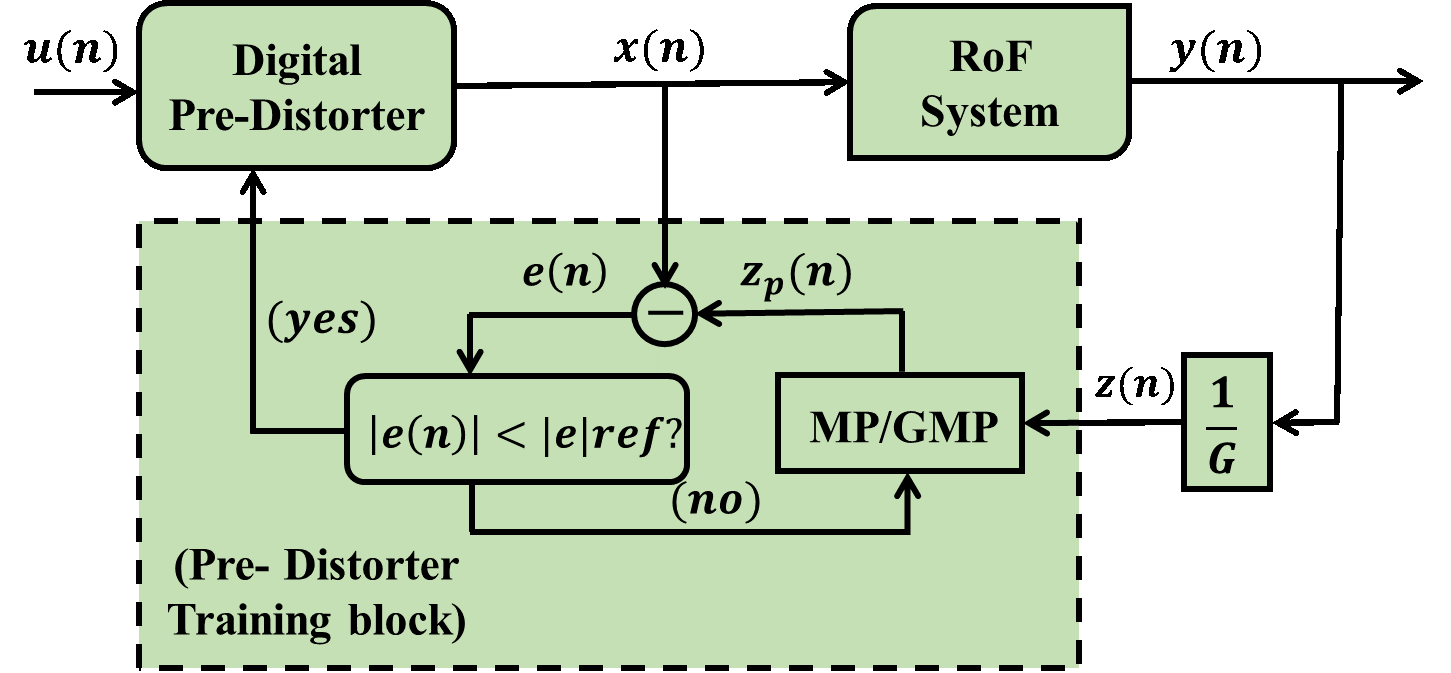Figure 2. DPD identification for RoF utilizing ILA

3. Digital Predistortion Model

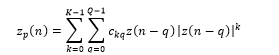 Memory Polynomial (MP) model is referred as an inverse non-linear model that has been exploited previously as a powerful model for both, inverse and direct modeling of power amplifier (PA) nonlinearities. Applying this model for RoF has an additional advantage since memory less model might have problems to characterize the electro-optical (EO) conversion phenomena accurately [34]. The MP model is generally referred as a compromise between memoryless nonlinearity and full Volterra series due to presence of diagonal memory. The output in this case is referred as:

      Here  represents order of non-linearity,  is referred as the memory depth,  represents the predistorter input sequence and  denotes the model coefficients.

1. Generalized Memory Polynomial (GMP) Model

      The use of Generalized Memory Polynomial (GMP) model has been widely utilized for the linearization of PAs [35]. However, GMP has not been yet evaluated for RoF with varying lengths. The GMP model basis functions possess memory for both, for the diagonal terms as well as for the crossing terms i.e., , where . The output of the post inverse block  modeled with GMP can be expressed as: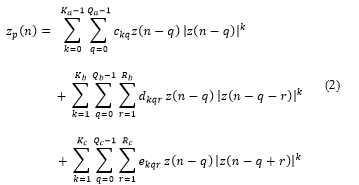

where represents the DPD output and input respectively. Similarly, and   denotes the complex coefficients for the signal and the envelope; signal and lagging envelope and signal and leading envelope respectively.  represents the index of nonlinearity, and  represents the indices of the memory.  While , ,  are the maximum orders of nonlinearity,  are the memory depths, while  and  exhibits the lagging and leading delay tap lengths, respectively. GMP has been applied choosing = = = , = = =  and .

The main objective of the predistorter is to minimize the error ( ) between the  and the input  of the RoF system.

4. Estimation Algorithm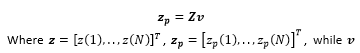

There are number of least squares (LS) algorithm for estimation of model coefficients that take the linear weighting of nonlinear signals [36]. The formulation of the estimation initiates with collecting the coefficients e.g., , and  in to a R × 1 vector .  represents the total number of coefficients.  means  a signal whose time will sample over the same period. Considering (2), coefficients  denotes the signal .  characterizes the collection of all such vectors into a x  matrix. Once the convergence condition is obtained, the output of the predistorter training block becomes:   and hence . For total samples , the output can be written in the following way:

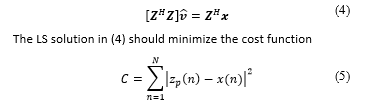The LS solution in (4) should minimize the cost function

The advanced variations to Volterra series in form of MP, GMP and others increases the effectiveness of predistortion. However, this advanced variation can come in to existence by increasing the memory depth and nonlinearity order. However, this will extortionate the computational complexity and this has to be weighed against other simpler expediencies. Moreover, the performance would generally be more efficient if the predistortion model has higher number of coefficients. This means that while selecting the model and its complexity, a smart tradeoff between complexity and performance can be made accordingly. The effect of increase in complexity will be shown in Sec. 7.

5. Experimental Setup

The experimental test bed utilized for demonstrating and validating the proposed DPD technique is shown in Figure 3. The baseband LTE signal of 5-MHz with 64 QAM modulation format is emulated through a domestic software on MATLAB compliant with 3GPP release TS 36.104 V15.2.0 [37]. The signal is oversampled at 38.4 MSa/s. After this, the sampled sequence of signals passes through the DPD block, which is then RF-transformed at 800 MHz by a Vector Signal Generator (VSG) (see Figure 3) and is then sent to the optical link.

There are two different optical links that are considered for testing DPD sequentially. In the first, a Single Mode VCSEL (Optowell), that operate at 850-nm, which is followed by a fiber span (SSMF) and a PIN photodiode, having 2.5 GHz bandwidth and responsivity factor of 0.6 A/W.  The SSMF for varying lengths has been utilized so that the effect of length on the DPD technique can be observed. In the second a 850-nm MM VCSELs in combination with MMFs was tested, maintaining the same photodetector of the other link.

The reason performing the test with reference to the two RoF configurations is related to the fact that each one of them presents aspects that, according to the particular applicative context, may make it preferable with respect to the other. The SM-VCSEL-SSMF based link can indeed feature convenience in terms of cost and flexibility, because of the lower cost per meter of SSMF with respect to MMF, and because of the huge transmission bandwidth of the SSMF. The MM-VCSEL-MMF based link can take advantage of a typically higher dynamic range and emitted/coupled power of the MM-VCSEL over MMF with respect to the SM-VCSEL over SSMF case.

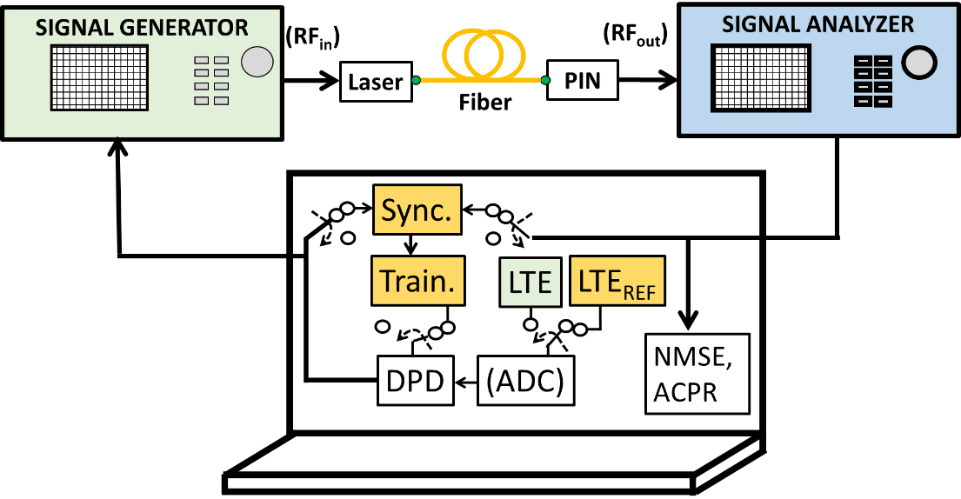Figure 3. Experimental evaluation comprising of  DPD training and application phase.

The reason performing the test with reference to the two RoF configurations is related to the fact that each one of them presents aspects that, according to the particular applicative context, may make it preferable with respect to the other. The SM-VCSEL-SSMF based link can indeed feature convenience in terms of cost and flexibility, because of the lower cost per meter of SSMF with respect to MMF, and because of the huge transmission bandwidth of the SSMF. The MM-VCSEL-MMF based link can take advantage of a typically higher dynamic range and emitted/coupled power of the MM-VCSEL over MMF with respect to the SM-VCSEL over SSMF case.

The process of predistortion is carried out in two steps. The first step is referred as a training phase. In training phase, the parameter identification for predistorter is carried out as referred in Figure 2. During the training phase, reference LTE frames are utilized (see LTE_REF block in Figure 3). Primarily, input and output signals are synchronized i.e. time aligned (see Sync. in Figure 3). This block finds the time delay estimation by utilizing the Synchronization Signals (Primary and Secondary) accessible in the LTE framework. Then, the predistorter coefficients are procured through the PD models utilized (see Train. in Figure 3).

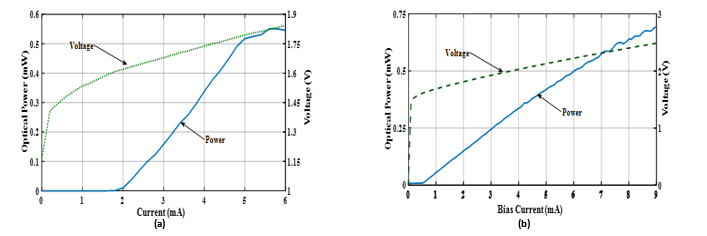Figure 4. L-I-V characterization utilized in the evaluation of DPD experiments for (a) SM-VCSEL and (b) MM-VCSEL.

In the second step i.e. the testing phase, the training coefficients obtained in previous step are utilized to apply DPD in MATLAB. This means that all switches are turned to opposite position in Figure 3 and the testing is done for LTE frames followed by sampling, pre-distortion, and then uploaded to the Vector Signal Generator (VSG). Finally, they are channelized through the optical link and performance metrics are compared with the one without predistortion. It must be noted that the DPD testing and validation is not only evaluated for the reference LTE signals that were used not only for training, but also for generalized LTE frames.

As mentioned, the quantities utilized to evaluate the effects of the DPD introduced are ACPR and the NMSE. At first, the efficiency of the proposed methods are presented by the ACPR that computes the distortion components outside the useful signal bandwidth. It is expressed as [1]: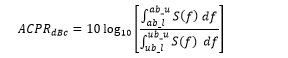

where  and  are the lower and upper frequency limits of the adjacent channel;  and  are the frequency bounds of useful bands. denotes Power Spectral Density (PSD) of the output signal .

NMSE is defined as follows [27]:

The NMSE value is estimated between  and  of the RoF where   embodies the total signal length.

Exploiting these definitions, ACPR and NMSE are calculated for the predistorted and without predistortion output signals. The comparison of the evaluated quantities is presented in the next section. The description of the specifications utilized are given in Table 1.

6. Results and Discussion

      The efficacy of the linearization method is appraised and brought into discussion in this section. A primary attention should be given while selecting the parameters of the predistorter such as memory depth ( ) and nonlinearity order ( ) (see Sec. 5 for the details).

Table 1: System Parameters

Optical Link Component	Parameters Values
Laser	SM-VCSEL Wavelength= 850 nmRIN = -130 dB/HzMM-VCSEL Wavelength= 850 nm RIN = -125 dB/Hz
Fiber	SSMF Maximum Length = 1.5 Km Attenuation = 2.5 MMF Maximum Length = 1 Km Attenuation = 2.5
Photo-detector	Responsivity = 0.6 A/W Bandwidth = 2.5 GHz

The L-I-V characteristic curve of SM-VCSEL and MM-VCSEL utilized are illustrated in Figure 4 (a) and (b) respectively. In SM-VCSEL, the maximum saturation current ( ) is 5 mA while threshold current ( ) is 2 mA. The bias point ( ) is chosen at 4 mA.

Similarly, In case of MM-VCSEL, the ( ) is 8 mA and threshold current ( ) is 0.8 mA. The bias point ( ) is chosen to be 4 mA. The signals having higher PAPR will give rise to higher distortions owing to small dynamics.  The PAPR of signal utilized is 9.1 dB

As explained in Sec. 5, the predistorter complexity is dependent upon the model and order of  and  chosen. In order to show the trend of this fact, Figure 5 elaborates the experimental NMSE results for different choices of  and  using both models.

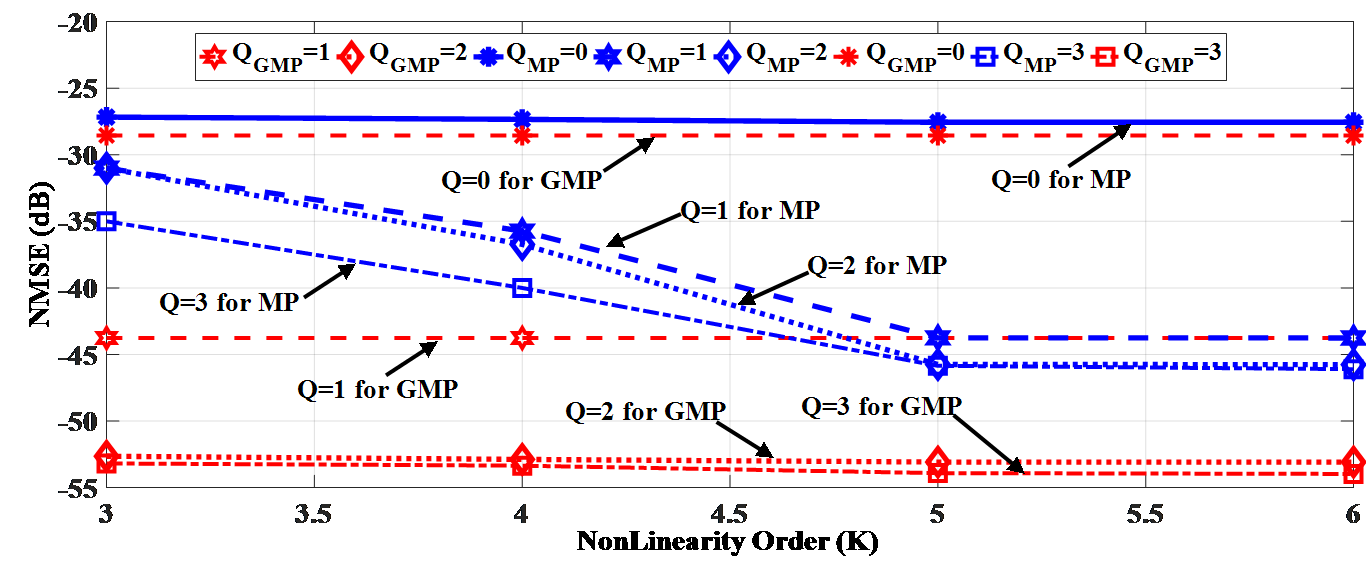Figure 5. Normalized Mean Square Error results with varying values of memory depth  and Nonlinearity Order .

The evaluation in Figure 5 has been done for varying orders of   (0, 1, 2 & 3) and non-linearity  (3, 4, 5 & 6) by applying a higher  RF input power (0 ). It can be perceived that GMP results in higher reduction of NMSE in comparison to MP at lower orders of . From this initial finding, the optimal values are chosen, resulting from a tradeoff between performance achieved and complexity required to the system.

 In addition to NMSE, to show the effect of increasing complexity of the proposed distorter, keeping the value of  fixed, Figure 6 represents the ACPR for MP ( ) and GMP ( ) for 1 Km of SSMF. It is perceived that ACPR for MP model doesn’t satisfies 3GPP ACPR requirement for MP (both  ) after -5 dBm of input power. While, GMP with  satisfies the requirement, however, it is exactly on the borderline at 0  of RF input power.

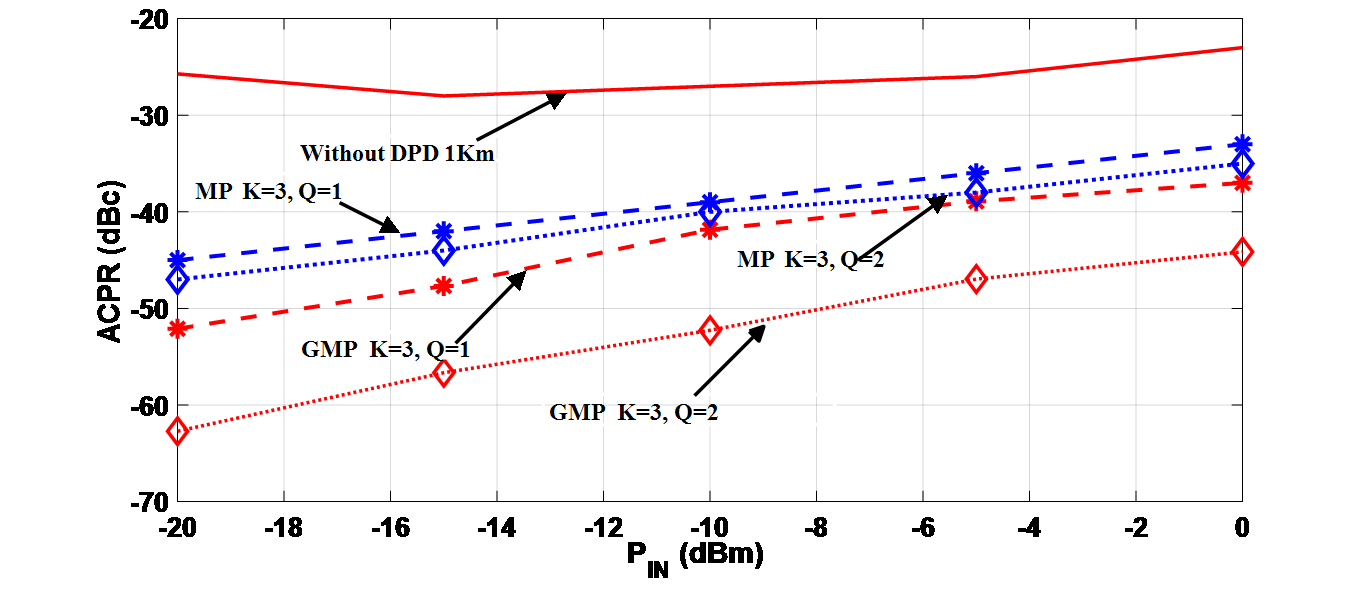Figure 6. ACPR outcomes vs. input RF power. ( =1,2, R=1 and =3 for MP & GMP).

Considering GMP with , the ACPR is well below the requirement set by 3GPP, hence the higher complexity enhances the performance.  This demonstration shows that the performance can be enhanced at the cost of higher complexity of the PD model.

Similarly, the Power Spectral Density (PSD) of the received sequence is analyzed when both models are implemented. The length is fixed to 1 Km and RF input power is 0 dBm. The results have been arranged for comparison of MP and GMP with same order of  and .

Consider Figure 7(a), the DPD for received output signal is demonstrated for both models by fixing K=3 and Q=1. It is noticeable that GMP has higher reduction in spectral regrowth reduction as compared to MP. Then, in order to highlight the effect of increasing the complexity order, the PSD of GMP and MP are compared for =3 and =2 in Figure 7 (b). This shows that DPD for =3 and =2 is stronger as compared to =3 and =1 due to which spectral regrowth reduction in latter case is higher. Similarly, GMP for =3 and =2 results in ACPR of -44 dBc as compared to -37 dBc when GMP is utilized for ( =3 and =1). This substantiates that GMP has better ACPR reduction than MP. This conclusion seems justified due to the fact that GMP carries memory not only in the diagonal but also in the crossing terms.

In light of this discussion and results in the Figure 5, 6 and 7, GMP with optimal values  keeping fixed have been selected from a tradeoff between performance achieved and complexity required to the system.

 In Figure 8 (a) and (b), the ACPR experimental outcomes for several RF input powers ( ) are reported for SM-VCSEL with SSMF and MM-VCSEL with MMF respectively.  First consider Figure 8 (a), there are three different cases discussed: Patch cord (Back to back), 1 Km fiber length and 1.5 Km fiber length case. By increasing the length of the fiber, the leakages in adjacent channels rise and therefore the worsening occurs with higher lengths. By employing linearization, it can be seen that fiber length with different lengths have different linearization profiles. For instance, let’s consider 1.5 Km length case, the ACPR without linearization at 0 is -18 , and with linearization employed, it is reduced by 22 to -40 .

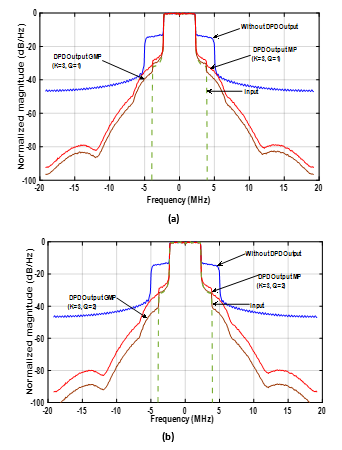Figure 7. PSD evaluation of output signal without and with DPD (MP/GMP) 0  for 1 Km SSMF with SM-VCSEL having: (a) Q=1, R=1, K=3 and (b) Q=2, R=1, K=3.

In case of Figure 8 (b), four different lengths have been shown up to 1 Km. For 1 Km length, the uncorrected ACPR at 0 dBm is around -22 dBc while the linearization results in a significant reduction to -36 dBc.

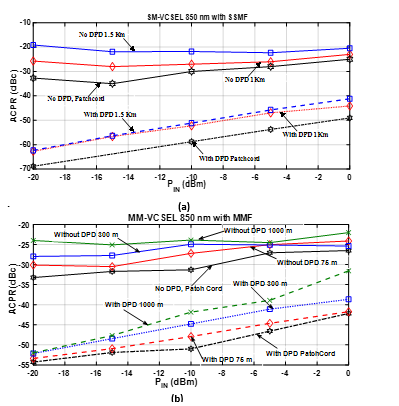Figure 8. ACPR results  vs. varying input signal power using ( =2 and =3 for GMP) for (a) SM-VCSEL with SSMF and (b) MM-VSEL with MMF.

 It can be deduced from the trend in Figure 8 (a) and (b) that the proposed DPD technique linearizes the length cases as well. Indeed, linearizing the laser nonlinearity is primary aim of the short link lengths, however, in addition to an optical channel consisting in a fiber patch cord (few meters of length), the proposed technique works efficiently for longer fiber lengths.

It must be put into evidence that linearization method has been evaluated for conditions which are very critical such as high PAPR and   close to the threshold with optimal values of K and Q. If these critical conditions are relaxed, this will lead to better linearization performance of the predistorter.

Figure 9 represents the AM-AM and AM-PM statistics with and without the linearization employed for the RoF link consisting of 1 Km SSMF and SM-VCSEL. It can be seen that after DPD, the AM/AM is now a straight line and the phase difference is reduced to within 2 degrees.

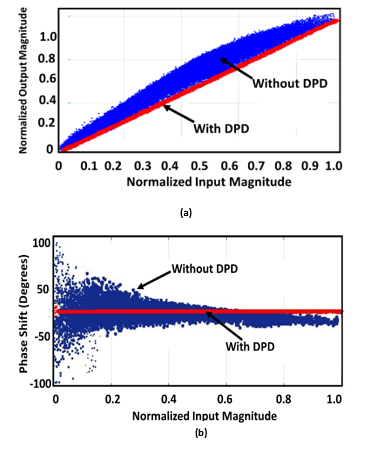Figure 9. (a) AM-AM and (b) AM-PM plots for SM-VCSEL at 1 Km of SSMF for 0 dBm of input RF power with and without DPD.

Table 2 reports the results of the proposed technique, referred to 1 Km of link length with 0 dBm. The results are summarized for MP and GMP with =3 and =2 in terms of ACPR and NMSE. The suggested technique linearizes the SM-VCSEL link and MM-VCSEL.

Table 2. Linearization performance for proposed DPD ( = 0 dBm, Link length= 1 Km)

Model	SM-VCSEL		MM-VCSEL
	NMSE (dB)	ACPR (dBc)	NMSE (dB)	ACPR (dBc)
Without  DPD	-19.86	-20	-17.63	-22.04
(b) With GMP (K=3, Q=2)	-41.548	-44	-33.18	-36
With MP (K=3, Q=2)	-31.25	-35	-30.14	-29

Indeed, Table 2 suggests that linearization with GMP is better than MP for link length of 1 Km (SM for SM-VCSEL and MM for MM-VCSEL). The reduction in ACPR and NMSE for SM-VCSEL is 22 and 20 dB respectively. While, for MM-VCSEL the improvement in ACPR and NMSE is 14 and 16 dB respectively.
This suggests that for SM-VCSEL, the linearization is better than MM-VCSEL for same parameters of data. The improvement for MM-VCSEL is different from SM-VCSEL because the nonlinearities of two lasers are different. It should be noted that MM-VCSEL can achieve higher linearization by selecting appropriate sets of coefficients.

Note that in an applicative scenario, the process of DPD may be positioned at the Central Office (CO), e.g. where BBUs are placed (see Fig. 1) and compensate the RoF Downlink nonlinearities. A periodical re-training of the Digital Predistortion system is in this case necessary, requiring however a negligible time with respect to the time of normal operation of the RoF system. Various methods  can be validated for enforcing the periodical training phase. Namely, if a RoF Uplink is applied, the nonlinearities in this case be compensated  by a digital post distorter block located at a correspondent CO [38]. By utilizing this method, the RoF downlink nonlinearities can be accumulated at  BBU which will decrease the cost and complexity of remote antenna unit.

The time devoted to the periodical re-training of the Digital Predistortion system would in any case remain negligible with respect to the time of normal operation of the RoF system, still allowing its adoption in real applicative scenarios. Similarly, it is possible to utilize an additional photodiode in a base station and feedback the laser nonlinearities and approximating that laser is the main cause of nonlinearity in the RoF link.

Note also that the proposed predistortion method can be applied also to LTE signals of larger bandwidth. The polynomial models nonetheless would require higher values of  &  with respect to the case presented in the submitted work.

Considering the LTE signal bandwidth and higher modulation format, they would result in a higher PAPR of the transmitted RF signal [39]. At the same time, the increase in bandwidth also determines a correspondent increase in the overall base-band memory of the system to be taken into account by the model.

The polynomial models proposed can still be applied in these operating conditions. They nonetheless would require higher values of the  &  with respect to the case presented in the submitted work.

These requirements would impact the cost of the DPD implementation, which would be higher due to the higher sampling rate of ADCs, and higher computing capabilities of FPGAs.

7. Conclusions

This article proposes a Digital Pre-Distortion mechanism for linearizing VCSEL based RoF links with different characteristics specifically link lengths. The proposed technique demonstrates a digital predistorter based on MP and GMP. The experiments have been prosecuted for systems based on SM-VCSEL followed by SSMF and on MM-VCSEL followed by MMF. The signal transmitted was a 5-MHz Bandwidth 64 QAM LTE signals and different link lengths have been considered. The performance has been explored in terms of ACPR and NMSE showing that for a link length up to 1 Km, both SM-VCSEL and MM-VCSEL can be linearized in good proportion. Particularly, utilizing SM-VCSEL, GMP results in 22 dBs of reduction in ACPR while MM-VCSEL results in 14 dBs of reduction in spectral regrowth. The results testify an encouraging link performance with low complexity of the predistorter model. It has been demonstrated for the first time that GMPs achieves superior linearization as compared to MP for link lengths up to 1.5 Km.

1.  M. U. Hadi et al., “Experimental evaluation of digital predistortion for VCSEL-SSMF-based Radio-over-Fiber link,” 2018 International Topical Meeting on Microwave Photonics (MWP), Toulouse, France, 2018, pp. 1-4.
2.  A. Gupta et al., “A Survey of 5G Network: Architecture and Emerging Technologies,” IEEE Access, Vol. 3, p. 1206-1232 (2015).
3.  Muhammad Usman Hadi, Hyun Jung, Salman Ghaffar, Pier Andrea Traverso, Giovanni Tartarini, Optimized digital radio over fiber system for medium range communication, Optics Communications, Volume 443, 2019, Pages 177-185, ISSN 0030-4018, https://doi.org/10.1016/j.optcom.2019.03.037.
4.  K. Y. Lau, “RF transport over optical fiber in urban wireless infrastructures,” in IEEE/OSA Journal of Optical Communications and Networking, vol. 4, no. 4, pp. 326-335, April 2012.
5.  Y. Shi ; D. Visani ; C.M. Okonkwo ; H. Yang ; H.P.A. van den Boom ; G. Tartarini ; E. Tangdiongga ; A.M.J. Koonen “First demonstration of HD video distribution over large-core POF employing UWB for in-home networks,”, 2011 Optical Fiber Communication Conference and Exposition and the National Fiber Optic Engineers Conference, pp 1-3 (2011)
6.  Y. Shi et al., “Ultrawideband Signal Distribution Over Large-Core POF for In-Home Networks,” in Journal of Lightwave Technology, vol. 30, no. 18, pp. 2995-3002, Sept.15, 2012.
7.  Hadi, M., Aslam, N. & Jung, H. (2019). Performance Appraisal of Sigma Delta Modulated Radio over Fiber System. Journal of Optical Communications, 0(0), pp. -Jan. 2019, from doi:10.1515/joc-2018-0227
8.  Hadi, M., Jung, H., Traverso, P., et al. (2019). Digital Radio Frequency Transport over Optical Fiber for 5G Fronthaul Links. Journal of Optical Communications, 0(0), pp. – Apr. 2019, from doi:10.1515/joc-2019-0051
9.  Hadi, M., Hadi, M., Aslam, N., et al. (2019). Experimental Demonstration of MASH Based Sigma Delta Radio over Fiber System for 5G C-RAN Downlink. Journal of Optical Communications, 0(0), pp. -. Retrieved 23 Feb. 2019, from doi:10.1515/joc-2019-0011
10. J. Nanni et al., “VCSEL-Based Radio-Over-G652 Fiber System for Short-/Medium-Range MFH Solutions,” IEEE/OSA J. Lightw. Technol, vol. 36, pp. 4430-4437, Oct.1, 2018.
11.  D. Visani, G. Tartarini, M. N. Petersen, L. Tarlazzi and P. Faccin, “Link Design Rules for Cost-Effective Short-Range Radio Over Multimode Fiber Systems,” in IEEE Transactions on Microwave Theory and Techniques, vol. 58, no. 11, pp. 3144-3153, Nov. 2010
12.  D. Visani et al.: Wired and wireless multi-service transmission over 1mm-core GI-POF for in-home networks, Electron. Lett., vol. 47, pp.203-205, Feb. 2011
13.  D. Visani et al., “ 3×2N-QAM Constellation Formats for DMT Over 1-mm Core Diameter Plastic Optical Fiber”, IEEE Photonics Technology Letters, 23, pp. 768-770 (2011).
14.  J. A. Tatum et al., “VCSEL-based interconnects for current and future data centers,” J. Lightw. Technol., vol. 33, no. 4, pp. 727–732, Feb. 15, 2015
15.  J. Nanni et al., “Modal noise in 850nm VCSEL-based radio over fiber systems for manifold applications,” Proc. Fotonica AEIT Italian Conference on Photonics Technologies, Turin, 2015, pp. 1-4.
16.  M.Sauer, A. Kobyakov, and A.B. Ruffin, “Radio-over-fiber transmission with mitigated stimulated brillouin scattering,”, IEEE Photonics Technology Letters, vol.19, no.19, pp. 1487–1489, Oct 2007..
17.  G. Tartarini and P. Faccin, “Efficient characterization of harmonic and intermodulation distortion effects in dispersive radio over fiber systems with direct laser modulation,” Microwave and Optical Technology Letters, vol. 46, no. 2, pp. 114–117, 2005.
18.  P. M. Sevila, V. Almenar, and J. L. Corral, “Transmission Over SSMF at 850 nm: Bimodal Propagation and Equalization,” IEEE/OSA J. Lightw.Technol., vol. 35, no. 19, pp. 4125–4136, Oct 2017
19.  J. Nanni et al., “Modal Noise Mitigation in 850-nm VCSEL-Based Transmission Systems Over Single-Mode Fiber,” in IEEE Transactions on Microwave Theory and Techniques, vol. 64, no. 10, pp. 3342-3350, Oct. 2016
20.  J. Weiss, “Analog Optical RF-Links for Large Radio Telescopes,”IEEE BiCMOS and Compound Semiconductor Integrated Circuits and Technology Symposium (BCICTS), San Diego, CA, 2018, pp. 24-27. doi: 10.1109/BCICTS.2018.8551058
21.  D. Visani et al., “Wired and wireless multi-service transmission over 1mm-core GI-POF for in-home networks,” in Electronics Letters, vol. 47, no. 3, pp. 203-205, 3 February 2011.
22.  C. Wang et al., “Machine Learning Detection for DMT Modulated 112-Gbps VCSEL-MMF Optical Interconnection,” Asia Communications and Photonics Conference (ACP), Hangzhou, 2018, pp. 1-3.
23.  W. P. Ng, T. Kanesan, Z. Ghassemlooy and C. Lu, “Theoretical and Experimental Optimum System Design for LTE-RoF Over Varying Transmission Span and Identification of System Nonlinear Limit,” in IEEE Photonics Journal, vol. 4, no. 5, pp. 1560-1571, Oct. 2012.
24.  S. F. Yu, “Nonlinear dynamics of vertical-cavity surface-emitting lasers,” in IEEE Journal of Quantum Electronics, vol. 35, no. 3, pp. 332-341, March 1999.
25.  Roselli, L., Borgioni, V., Zepparelli, F., Ambrosi, F., Comez, M., Faccin, P., Casini, A.: Analog laser predistortion for multiservice radio-over-fiber systems. IEEE J. Lightw. Technol. 37(5), 1211-1223 (2003)
26.  Zhu, R., Zhang, X.: Broadband predistortion circuit design for electro-absorption modulator in radio over fiber system. In Proceedings of the Optical Fiber Communications Conference and Exhibition(OFC), San Francisco, CA, USA (2014).
27. F. Fuochi, M. U. Hadi, J. Nanni, P. A. Traverso and G. Tartarini, “Digital predistortion technique for the compensation of nonlinear effects in radio over fiber links,” IEEE 2nd International Forum on Research and Technologies for Society and Industry Leveraging a better tomorrow (RTSI), Bologna, 2016, pp. 1-6.
28.  A. Hekkala et al., “Predistortion of Radio Over Fiber Links: Algorithms, Implementation, and Measurements,” in IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 59, no. 3, pp. 664-672, March 2012.
29.  Mateo, C., Carro, P.L., Garca-Dcar, P., De Mingo, J., Salinas, I.: Radio-overfiber linearization with optimized genetic algorithm CPWL model. Opt. Express. 25(4). pp. 3694-3708, Feb. 2017.
30.  M. U. Hadi, P. A. Traverso, G. Tartarini, O. Venard, G. Baudoin and J. Polleux, “Digital Predistortion for Linearity Improvement of VCSEL-SSMF-Based Radio-Over-Fiber Links,” in IEEE Microwave and Wireless Components Letters, vol. 29, no. 2, pp. 155-157, Feb. 2019.
    doi: 10.1109/LMWC.2018.2889004
31.  M. Abi Hussein, V. A. Bohara and O. Venard, “On the system level convergence of ILA and DLA for digital predistortion,” 2012 International Symposium on Wireless Communication Systems (ISWCS), Paris, 2012, pp. 870-874.
32.  D. Morgan, Z. Ma, J. Kim, M. Zierdt, and J. Pastalan, “A generalized
    memory polynomial model for digital predistortion of rf power amplifiers,” Signal Processing, IEEE Transactions on, vol. 54, no. 10, pp. 3852–3860, Oct. 2006.
33.  L. Ding, G. Zhou, D. Morgan, Z. Ma, J. Kenney, J. Kim, and C. Giardina, “A robust digital baseband predistorter constructed using memory polynomials,” Communications, IEEE Transactions on, vol. 52, no. 1, pp. 159–165, Jan. 2004.
34.  Hekkala, A., Lasanen, M.: ‘Performance of adaptive algorithms for compensation of radio over fiber links’. Proc. IEEE Wireless Telecommunication Symp., Prague, Czech Republic, April 2009, pp. 1–5
35.  D. Morgan, Z. Ma, J. Kim, M. Zierdt, and J. Pastalan, “A generalized memory polynomial model for digital predistortion of rf power amplifiers,” Signal Processing, IEEE Transactions on, vol. 54, no. 10, pp. 3852–3860, Oct. 2006.
36.  L. Guan, and A. Zhu, “Optimized Low-Complexity Implementation of Least Squares Based Model Extraction for Digital Predistortion of RF
    Power Amplifiers,” IEEE Trans. Microw. Theory Tech., vol. 60, no. 3, pp. 594-603, Mar. 2012.
37.  3GPP TS36.104 V15.2.0, Evolved Universal Terrestrial Radio Access (E-UTRA) User Equipment (UE) Radio Transmission and
    Reception (Release 15), March 2018.
38.  L. C. Vieira and N. J. Gomes, “Experimental demonstration of digital predistortion for orthogonal frequency-division multiplexing-radio over fibre links near laser resonance,” in IET Optoelectronics, vol. 9, no. 6, pp. 310-316, 12 2015. doi: 10.1049/iet-opt.2014.0160
39.  M. U. Hadi, “Extending the benefits of LTE to unlicensed spectrum,” 2015 International Conference on Information and Communication Technologies (ICICT), Karachi, 2015, pp. 1-3. doi: 10.1109/ICICT.2015.7469592

(Click Here)

(Click Here)