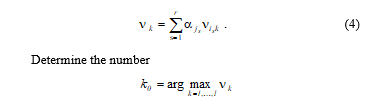1. Introduction

This study is an extension of work originally presented in International Russian Automation Conference [1]. The study gives a new vector of application of fuzzy mathematics methods in the analysis of complex multifactor technical systems, including chemical-technological system (СTS), for their identification and pre-experimental research. These systems, as a rule, are described by fuzzy information: the presence of linguistic descriptions, intervals, lack of data, incompatible research results, conflicting expert opinions, etc. Under these conditions, mathematical modeling using this information also has a fuzzy nature and a multiplicity of solutions. Nevertheless, the use of fuzzy mathematics, fuzzy modeling allows at the preliminary stage to choose the optimal and economical strategy of the experiment and evaluate the expected technical result, which is directly related to product quality. It should be noted that the use of fuzzy set (FS) for the preparation of initial information in the simulation of СTS has recommended itself from the positive side, as a form of theoretical analysis of polymer composition (PC) and finding the relationship between the components and properties of the polymer system as a whole. Here, a prerequisite is the identification and ranking of the technical functions of the ingredients of the PC. Managing the properties of polymer composite material (PCM) is an important task of chemical technology, it can be extended to: oil and gas processing (primary separation, refining, age hardening), petrochemical and organic synthesis, biotechnology, the technology of high-molecular substances, the technology of processing plant and animal raw materials and etc. [2].

The formation of the PC optimization problem and its solution is based on the “composition – property – quality – application” dependence and provides for the selection of a certain number of ingredients with the necessary technical functions using fuzzy modeling. In this paper, this idea is extended to the PCM analysis.

Raw PC, in other words, mixtures, are complex systems. They are based on polymer matrices in which various ingredients are added. The interaction between such matrices, their structure and composition also depend on the chemical and technological processes of their processing. PC-derived composites are also complex heterogeneous systems and can be divided into five leading classes:

1. Matrix, consisting of a continuous phase (matrix) and a dispersed phase (discrete particles) (dispersed — hardened composite materials).
2. Compositions with fibrous fillers.
3. Mixed compositions.
4. Compositions having an interpenetrating structure of two or more continuous phases.
5. Layered PCMs.

Considering the special interest of researchers and the market of consumers of polymer products to nanotechnology, let us mention the polymer matrix of the “polymer matrix – additive (filler)” composition, in which 2D and 3D nano-ingredients are used as fillers — graphene and carbon nanotubes. Here, mathematical modeling can be conducted based on the analysis of ingredients in the direction of predicting the level of physical and mechanical properties, depending on the number and size of nanoparticles and the parameters of the polymer matrix of a stable configuration. This direction is at the beginning of development, therefore, in most cases, problems are solved on the basis of experiments [3, 4]. Here the applicability of fuzzy mathematics is quite possible when calculating and analyzing results. Thus, the PC is ultimately a multi-component, inhomogeneous system, the characteristics of which do not allow to calculate the exact values of technical effects by its component. The versatility of the situation emphasizes the fact that in addition to a large set of active and inactive fillers, modern technology with a different purpose gives rise to the use of new modifying additives, a brief description of which is proposed below. In parentheses are their possible concentrations in the PC.

Light stabilizers allow for a long time to maintain the original color of the product and its mechanical strength, providing protection from ultraviolet rays. Here you can point to derivatives of benzonitrizol, benzophenol, nickel and cobalt salts of substituted phenols, etc. It has been established experimentally that they are effective even at very low concentrations (0.1 –5.0%).

Antioxidants prevent thermo-oxidation and slow down destruction during extrusion and injection molding. Also, these additives are used to protect the polymer when processing in aggressive environments. The mixtures compounds of phenols and phosphides (0.1 – 2.0%) are the most popular here.

Plasticizers are low molecular weight organic substances that, when introduced into the composition at the preparation stage, reduce the interaction between adjacent macromolecules. At the same time, common plasticizers include esters of organic and inorganic acids, such as dibutyl phthalate, di-(2-ethylhexyl) phthalate, dibutyl sebacate, tricresyl and tributyl phosphate, refined products, (petroleum oil), coal and wood materials (cumarone indene resin, rosin, etc), epoxidized vegetable oils, etc. The temperature of decomposition of plasticizers should be higher than the processing temperature of PC (0.1 ­­– 45.0%).

Combined additives (light stabilizer + antioxidant + dye, etc.) are widely used in the production of agricultural films. They allow to use the polymer for its intended purpose after recycling (0.1 – 45.0%).

Flame retardants are the most important additive limiting the flammability of PCM. Special flame retardants are used for the production of non-combustible and low-flammable films, sheets and molded products. They are divided into three large groups:

• chemically interacting with the polymer;
• intuminescent;
• additives mechanically miscible with polymer.

Flame retardants are most often halogen-containing and phosphorus-containing compounds, as well as metal hydroxides and other inorganic compounds (0.1 – 3.0%).

Antistatics can get rid of the static effect. For example, in the manufacturing of cases for audio and video equipment. Commonly used antistatic agents include alkylamines (up to 3.0%).

Slip agents are an internal lubricant in a polymer matrix that reduces melt viscosity, improves extrusion performance, makes the surface smoother, shinier and glossy, and reduces the coefficient of friction of products. Active ingredients are derivatives of higher fatty acids (depending on technology).

Anti-blocking additives prevent sticking, that is especially important in the production of polypropylene films. The packages made of a film with such additives are easily opened. Package walls do not stick together. Active ingredients are silicic acid or amide waxes (0.1 – 0.3%).

Antislips are additives that are similar in properties to antiblocking. They give the surfaces of the films roughness. They are used in the manufacturing of packaging, bags for packing bulk products and other products. One of the antislips is ultra high molecular weight polyethylene (0.1 – 0.3%).

Antiseptics prevent the biological destruction of PCM (up to 2.0%).

Nucleates affect the supramolecular structure of the polymer matrix, making it more fine-grained. At the same time, the crystallization time is significantly reduced, the product is cooled faster. In addition, the effect of greater transparency of the films is created. Nucleates are used exclusively for polypropylene (0.1 – 0.3%).

Foaming additives are used to manufacture porous polypropylene and polyethylene products. The structure of the matrix is loosened, the extensions disappear with the introduction of additives. They are designed to produce decorative films used in the packaging of gift sets, as decorative ribbons, gaskets in cork and other purposes (depending on the requirements of technology).

Modifier in the production of stretch films. It gives them the effect of additional elasticity, and for some polymers, including polypropylene, impact resistance (no information).

This list is rapidly replenishing and expanding today, for example, so-called processing additives that improve the economy and technological parameters of processing activities (in each case individually) can be singled out separately.

Today, PC theory is an attempt to solve the problem of how the final physicochemical properties of finished products depend on the composition, chemical-technological and physical-technical parameters. The ultimate goal here is to obtain materials with desired properties. To achieve this goal it is necessary, setting the final properties of the designed material or product, to know the parameters of their manufacture.

General requirements for PC ingredients are as follows:

1. thermodynamic compatibility with the polymer matrix should be ensured, preferably before the formation of a molecular solution;
2. should not be volatile;
3. do not bleed out of the polymer matrix;
4. should be nontoxic, chemically and thermally resistant.

As an example (Table 1) [5], we consider the composition (in weight parts) of an electrically insulating PC from the Russian patent which is well illustrating the multifactorial nature of the identification problem and the versatility of PCM ingredients. And this is not the most difficult PC.

Therefore, for PCM ingredients, their effect on the polymer matrix is empirically determined. And to obtain a PC with the desired set of properties, both polymer matrices and individual ingredients are selected. The complexity of the problem is obvious, as is the complexity of the system.

It should be noted that for particular cases of the theoretical analysis of the properties of PCM, many CTS analysis methods are used: discriminant, factorial, regression, etc., to identify the control actions and calculate their consequences, while operating in numerical spaces [6 – 8]. But in the presence of nonnumeric, for example, linguistic parameters, such methods become of little use and require additional efforts to harmonize the source data and mathematical methods. Comparing and critically analyzing the existing mathematical approaches [2, 6 – 9] we can conclude that an important part of this problem is overcome by using FS for describing both numerical and nonnumeric parameters. The solution of the problem itself is carried out by methods of fuzzy mathematics. Important elements of the latter are increasingly being applied in the scientific analysis of the CTS [10 – 13].

Table 1: Composition of a Polymeric Composition (in Weight Parts)

Components	No.
	1	2	3	4	5	6	7
PVC S-70*	100	100	100	100	100	100	100
Dioctyl phthalate	40	–	–	–	70	–	–
Diisononyl phthalate	–	45		40	–	80	–
Trioctyltrimethyl metat	–	–	50	–	–	–	50
Isodecyldephenyl phosphate	–	–	–	20	–	–	15
Calcium carbonate	40	60	80	100	120	140	160
Tribasic lead sulfate	3	–	5	–	4	–	6
Dibasic lead phthalate	–	4	–	3	–	5	–
Antimony trioxide	3	4	5	6	7	6	8
Zinc oxide	2	3	4	6	8	2	4
Zinc borate	2	5	6	3	3	8	4
Diphenylolpropane	0.20	0.25	0.30	0.35	0.4	0.35	0.30
Magnesium hydroxide	20	–	40	25	60	–	80
Aluminium hydroxide	–	30	20	50	–	70	–
Metallic silver in the form of nanoparticles	0.001	0.005	0.01	0.015	0.02	0.025	0.03

* PVC S-70 – polyvinyl chloride polymer matrix, Russian brand S-70.

In connection with the above, let us point out that the management of PCM properties is possible in various theoretical and further practical ways, such as:

• pre-experimental heuristic identification,
• the choice of the polymer type,
• changes in production technology of polymer used as a matrix (polymerization, polycondensation, modification, crystallization, structuring),
• regulation of the concentration and technical functions of the ingredients,
• variation of composition and structure.

Among the newer modern experimental approaches to the management of PCM properties through the “composition – properties” relationship, for example, layer-by-layer deposition of polymers can be specified to control the conductivity of ophthalmic preparations through lenses [11], the regulation of technology to control the physicochemical properties of PCM [12 – 16 ], or increase, in the particular case, of the structural stability of such a biopolymer as DNA, when counter-ions are neutralized with the help of polyamines [15]. From what has been said, it is clear that controlling the properties of the polymer matrix, whether it be an olefin or DNA, is a separate scientific and technological task. Here, we have not found any works on the application of FS for the theoretical analysis of the polymer matrix — a full-scale experiment is fully used. So we have attributed points 4, 5 to the above list to our problems.

Here, the use of fuzzy analysis for the study of polymer systems and their particular case of PCM and comparison of mathematical procedures of fuzzy analysis [16, 17] made it possible to formulate the task of managing the properties of PCM and to obtain particular methods of its solution. Let us make the restrictions related to the subject area of this article and introduce it into the framework of the general task of studying CTS, while considering the PC as a system consisting of an undefined set and their number. Mathematical modeling and optimization of this CTS will be carried out under the conditions mentioned above, multicriteriality, incompleteness and vagueness of the initial information. This information can include the knowledge, experience and intuition of a specialist expert, which provides the basis for managing these systems — one of the main modern vectors of their development. We repeat that the identification of optimal and compromise technical solutions at the early stages of the formation of a plan for laboratory research and pilot product releases in world practice is known [18, 19], but it is still an urgent task focused both on the creation of new equipment and technology, and on the savings of intellectual and material resources. In principle, the problem of analyzing fuzzy data is relevant for analyzing the internal problems of the intelligent systems themselves, which are oriented toward interaction with both researchers and the consumer. As an example, one can cite a system for analyzing linguistic information for predicting the commercial attractiveness of goods [20] and other areas using problems with fuzzy data [21, 22].

The work of creating a fuzzy model is multidimensional and complex. It can be noted that in chemistry and technology, PCM tasks with fuzzy data are most of all:

• selection of compositions,
• evaluation of new materials properties,
• design of competitive technologies,
• consideration of possible environmental damage,
• safety accounting, etc.

Describing the problem of modeling CTS in this part, it is necessary to proceed from the fact that the very formulation of the problem of fuzzy modeling, computer implementation of calculations and their effectiveness can have, as discussed above, the nature of the set, which is largely determined by the formalization of the source data (parameters and conditions) and the adequacy of the test results obtained during the simulation. At the same time, depending on the level of fuzziness and the type of model obtained, the solutions may have different significance [22].

Let us add that modern research focused on processing fuzzy information uses the following route: “raw data – fuzzification –analysis – defuzzification – result”. At the same time, they formulate variables, including linguistic ones, and, using conventional methods of fuzzing terms, go to FS and further, as for example, in [23] analyze the resulting data model in a mathematical package [24]. Also fuzzy components are explored using intelligent systems. Since the considered approach focuses on certain subject areas, the formalization of information is carried out in accordance with the requirements of these areas using a mathematical apparatus. This is often beyond the power of ordinary users of intelligent systems. In such cases, it is offered either detailed manuals, or to fully automate the process.

We performed the real work, which is the software of the information system (IS) summarizing the information available in this part and using our own experience in solving such fuzzy problems. Here it will be possible, firstly, to automate the initial processing of the raw data (to carry out the fuzzification process) and, secondly, to analyze the solutions for the information support of researcher work. The second part is focused on a wide range of chemical-technological tasks, such as: classification, identification, examination and management of the CTS. The specific analysis methods discussed below are focused on relative data and have no substantive substantiation; therefore, they can be applied in other fields of science and technology. We also point out that to solve the problems of our profile, we used the latest advances in the field of FS analysis [25 – 29], interval mathematics [30], and others [31], however, a universal method for processing fuzzy data, we have not found neither in Russian nor in foreign practice, although research in this direction is being actively conducted, as an analysis of scientific and technical literature of recent years shows.

This paper takes into account the complexity of the system and the PCM analysis and is aimed at developing a methodology for formalizing the source data in the form of fuzzy numbers, defining a library of mathematical models for selecting ingredients from a given set. Ultimately, information is provided for the quantitative support of the decision to choose PCM. Also, the typing of the source data will allow to unify and algorithmize the process of automated analysis of the results of the experiment.

2. Research objective

Now we will set a more specific task of forming the initial data, and then the mathematical method of calculation. We point out the conceptual fuzziness that exists and arises when describing the PCM:

• the technical functions of the ingredients are not presented;
• in the description of the ingredients of their concentration in the PC are given in the form of intervals;
• the level of action of the technical function of additives is characterized linguistically and is not related with their concentration in PCM;
• the possible relationship between the physicochemical parameters of the additives themselves and PCM and the positive or negative chemical interaction between them is not indicated.

Considering these fuzzinesses, which are more practical in practical technologies, the description of the data about the PCM by fuzzy numbers and operations with them by the methods of fuzzy mathematics will be adequate techniques. In general, the quality management of PCM will be carried out according to the scheme proposed in Figure 1 using fuzzy data analysis techniques.

Note that the main requirements for the PCM are formulated by consumers (customers) and process engineers, taking into account industrial capabilities and needs, on their part introduce additional requirements. If the former determine the range and tolerances of physicochemical, mechanical, ergonomic, environmental and other operational characteristics; the latter proceed from technological limitations, polymer matrix synthesis processes (polymerization, polycondensation, modification) and processing: (melting, mixing, casting, molding, stamping, extrusion, etc.) The formulation of such requirements is made by experts in the relevant fields, and, in many cases, is cited in reference data sources.

We assume that the basic consumer requirements already exist. It is necessary to construct the composition of the PCM that best meets these requirements and select ingredients with certain technological and technical functions.

The management of the design and analysis process of the PCM itself is carried out by assessment and selection of:

• polymer matrix,
• ingredients (including fillers),
• coordination of concentrations,
• justification of processing technology.

These actions need to be carried out in concert, since the nature of each polymer matrix determines a unique combination of possible ingredients and their content. You can get far from optimal low-potential low-quality PCM even choosing a polymer matrix with good physico-chemical characteristics and using an unsuccessful set of ingredients.

The following route is proposed for creating an original technical solution:

1. The choice of the polymer matrix is carried out on the basis of the analysis of the achieved level of technology by a variable method from the available kits, most often from the brand kits.
2. Determination of technical functions and concentrations of ingredients and their combinations is carried out through technical expertise.
3. Specific representatives are selected from the known ingredients, taking into account the available possibilities, and the compliance index for each of them is calculated.
4. PC is numerically evaluated based on the properties of the selected components by calculating the PC compliance index and, if necessary, proceeds to step 1.

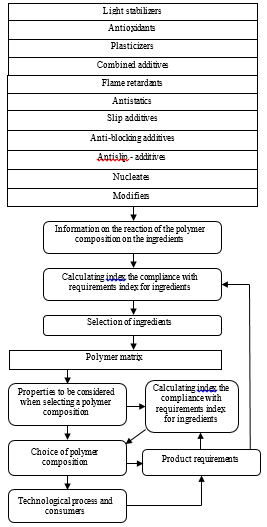Figure 1: Control Scheme of the Physicochemical Properties of PCM and the Quality of Polymer Products

5. The decision is made on further actions: the choice of the polymer matrix, the specific composition of the PC, the individual ingredient, changes in the technological regime, etc.

Actions under item 1 are related to the experience of the technologist and researcher, the availability of information and material resources. They are obvious and, we believe, comments do not require. The actions under item 2 can be implemented either by designers or directly by process engineers — experts in the field of chemistry and PCM technology. It can also use reference books, databases and knowledge bases or knowledge systems created on the basis of generalization of subject information. In any case, the technology of these actions goes far beyond the scope of this article and is not discussed in detail here.

This article discusses in more detail the steps in paragraphs 3, 4 and 5 related with solving the problems of evaluating the technical functions of ingredients in a given set for designing a PC, in the context of the decision to choose its composition. A solution to the problem of optimal PC selection using a given polymer matrix and variability of additives is also proposed. In the simplest case, it is CTS type “one polymer matrix + one functional additive” or “polymer matrix + filler + functional additive”. In the latter case, the “polymer matrix + filler” is considered inseparably. Then we will complicate the task.

We formulate the general task of determining compliance with the requirements of an abstract technical object and present the main points of its solution method, to assess the quality of the additive used to form a PC, and then the quality of PCM.

Let Q = (Q_ij), i = 1, …, n, j = 1, …, m be the matrix of input data describing the results of measurements or calculations of m characteristics of n representatives of a certain class of chemical systems s₁, …, s_n, Q_ij Î Q_j, where Q_j is a set of values representing numbers, sets, words, etc.

Here and below, we will illustrate the reasoning with an example of the choice of a flame retardant for a polymer matrix presented in the form of a fibrous substrate (Table 2). At the same time, since this is not significant for the description of the mathematical methodology, the names of chemical compounds, as well as the dimension of physicochemical parameters will be omitted. The point is that it is necessary for those given in Table 2 data to evaluate the PC system being formed and in some sense choose the best option. The choice of flame retardant as an illustration of FS application in this case is related to its technical function (see above) and cannot be considered accidental or abstract. The fact is that in the practice of chemistry and chemical technology of high-molecular compounds, imparting noncombustibility of PCM or a significant decrease in combustibility is one of the most urgent tasks, along with increasing the durability of polymer products.

Table 2: Abstracted Characteristics of Industrial and Laboratory Flame Retardants [25]

Compound no., i	Qi1	Qi2	Qi3
0 (Reference,  q/d)	1.0/8	1.5/8.5	21/10
1	19	12.1	9
2	18	10.7	9
3	18	3.7	14
4	6 – 10	6 – 10	15
5	18	2	9
6	3	3	10.6
7	1.0 – 1.2	2.67	15
8	1.0 – 1.2	1.5 – 2	9 – 11

It is clear that the method discussed below can be applied to any flame retardant, and in general, to an ingredient, both from the list discussed above and any other using any polymer matrix. The solution of the problem is divided into several stages, including: analysis of the initial data Q, construction of fuzzy numbers U, formalization of requirements in the form of fuzzy numbers, comparison of U with formal requirements, choice of PC, decision making.

3. Analysis of the source data

3.1.  Method Description

The purpose of this stage is to bring different types of data to one type in the form of a segment. We use the operator proposed earlier [31],  i.e. define the operator A, for this:

A(Q_ij) = [q_ij1; q_ij2], q_ij1, q_ij2 Î R, q_ij1 < q_ij2,

where R — set of real numbers.

It is not possible to define this operation precisely, since in practice Q_ij can be represented in any form, but first you can describe the solution for the most typical forms by creating a library of data models, and later, if necessary, expand the library, which will allow you to adapt the proposed approach to almost any type of source data. Consider the most common cases.

1. Q_ij — real number.
2. Q_ij — set of real numbers.
3. Q_ij — linguistic value.

For all these cases, it is proposed to use the following operator.

where

A₁: R×R⁺\{0} → Á, Á = {[a; b]| a, b Î R, a < b},

namely,

A₁(x, y) = [x – y; x + y], x Î R, y Î R⁺\{0};

A₂: Â → Á, Â = {X| X Ì R},

namely,

A₂(X) = [inf X; sup X], X Ì R;

A₃: t → Á₁, Á₁ = {[a; b]| [a; b] Ì [0; 1]},

namely,

A₃(t_k) = [e_k–1; e_k].

Operator A₃ requires additional explanations on the set of terms t. Let be Q_ij Î t = {t_k| k = 1, …, r}, and terms t_k are such that t₁ p … p t_r, where p is an ordering relation. We split the segment E = [0; 1] into r parts in accordance with the terms t_k, while maintaining the same order, i.e.

where E_k = [e_k–1; e_k], k = 1, …, r – 1, E_r = [e_r–1; e_r], 0 = e₀ < e₁ < < … < e_r = 1.

Illustrating with compound no. 1 from the example under consideration (Table 2), we obtain, for example, for parameter no. 1

Q₁₁ = 19, δ₁₁ = 1,

q₁₁₁ = 18, q₁₁₂ = 20,

i.e.

A₁(19, 1) = [18; 20].

Further, similar to [25], fuzzy numbers are given for q values: where q_ij = (q_ij1 + q_ij2)/2, δ_ij = (q_ij2 – q_ij1)/2, x Î R. Main provisions of fuzzification described in [25] are given in a more generalized form in clause 3.2.

As a result, a matrix of fuzzy numbers U(x) = (u_ij(x)), i = 1, …, n, j = 1, …, m (Table 3) is obtained.

Further it is necessary to formalize the requirements for representatives of the class of systems. In the context of our example it is necessary to formalize the operational requirements for PCM, for which can serve properties defined in statics and in the dynamics, for example degradation, such as durability and biodegradability. The latter is a time challenge. Characteristics must be expressed quantitatively and / or qualitatively. For further actions, we proceed in the same way as [31], namely, let us set a hypothetical fire retardant s₀, possessing such characteristics that fully meet the operational requirements (Table 2, fire retardant 0). At the same time, the characteristic q_0j reflects the required value, and δ_0j is the tolerance value, within which the value of the corresponding characteristic satisfies the requirements.

Table 3: Values of the Elements of the Matrix U(x) Calculated from the Table 2

No. compound, i	qi1/δi1	qi2/δi2	qi3/δi3
0 (Reference,  q/d)	1.0/8	1.5/8.5	21/10
1	19/1	12.1/0.1	9/1
2	18/1	10.7/0.1	9/1
3	18/1	3.7/0.1	14/1
4	8/2	8/2	15/1
5	18/1	2/0.1	9/1
6	3/1	3/0.1	10.6/0.1
7	1.1/0.1	2.67/0.01	15/1
8	1.1/0.1	1.75/0.25	10/1

3.2.  Computational experiment

To evaluate systems from a given class, we use the method described in [25], which consists of the following.

Let S = {s_i| i = 1, …, n} is a set consisting of n objects. For each object s_i, m characteristics Q_ij, j = 1, …, m are defined. Depending on the conditions of use, the set of considered characteristics may expand and contract, up to the introduction of chemical, biological, ergonomic and other properties. We select the reference object s₀ and its characteristics Q_0j, and s₀ can be either an element of the set S or not, it depends on the specific conditions of the problem and the preferences of the research or expert opinion. The characteristics of Q_0j are selected in such a way that s₀ is optimal in terms of the requirements for the quality of the object.

It is required to rank the elements of the set S according to the given m characteristics for compliance with the standard.

For each characteristic Q_ij we construct a FS, , i = 1, …, n, j = 1, …, m. To do this, we define the variables x_j with the range of values of G_j. Let the values of the variable x_j, satisfying the characteristic Q_ij, make up the segment X_ij. Then

X_ij = A(Q_ij).

We select the membership function m_ij for the criterion Q_ij. Based on the construction of the set X_ij we find that in the q_ij, function has a maximum point, within the set X_ij the membership function takes values greater than 0.5, and outside X_ij it is less than:

m_ij: G_j ® [0; 1],

m_ij(q_ij) = 1,

m_ij(x_j) ³ 0.5 Û x_j Î X_ij.

As a membership function, you can, for example, use the following functions:

, i = 0, …, n, j = 1, …, m.

As a result, we get FSs

= {x_j| m_ij(x_j)}, i = 0, …, n, j = 1, …, m.

We’ll calculate the degree of equality n_ij of the corresponding FS [26] to determine to what extent the characteristic of the object si is close to the characteristic of the reference object s₀: and the value 1 will correspond to absolute equality, and 0 to absolute inequality.

Further using the aggregate function (as such, we can take, for example, weighted voting), we’ll obtain an integral estimate n_i of the correspondence of the set of object characteristics s_i of the set of object characteristics s₀.

We’ll calculate the degree of equality n_ij of the corresponding FSs [32], using this method in our experiment, in order to determine to what extent the characteristics of flame retardant no. i is close to the characteristic reference no. 0:

For the membership functions of the reduced form [33], we have obtained that the maximin value is reached at the point:

Having conducted a weighted vote, we’ll obtain an integral assessment n_i of the correspondence of the set of object characteristics s_i  to the set of object characteristics s₀:

where a_j ³ 0, . The weights a_j are selected in accordance with the level of importance of each of the characteristics and are determined by the expert in the subject area so that the PC fully meets consumer requirements, technological process, etc. It is accepted here a₁ = a₂ = 0.33, a₃ = = 0.34. The results of calculations based on the data Table 2 are presented in Table 4.

Table 4: Evaluation of Fire Retardants to Compliance with Operational Requirements

Fire retardants no., i	νi
1	0.28
2	0.33
3	0.60
4	0.76
5	0.51
6	0.81
7	0.93
8	0.83

Thus, the no. 7 fire retardant is preferable from the point of view of the presented requirements.

The proposed computational model can form the basis for automated data analysis when choosing the optimal CTS, including with the participation of experts. The approximate route of operation of such an IS is shown in Figure 2. Here, the requirements for the evaluated objects (PCM) are set directly in the IS interface when formulating the initial task, allowing specialists to quickly adjust its formulation in the context of the research.

When generating generic CTS evaluation tasks, it is possible based on known experimental data to form a library (database) of expert assessments (along with the data model library), which will relieve the user of the IS from having to obtain or collect expert assessments and fully automate the evaluation process of a specific CTS.

Figure 2: Scheme of the Information Flow in the IS

4. The optimal choice of a single additive for the polymer composition

4.1.  Method Description

Let p_k, k = 1, …, l — be polymeric matrices, s_ik, i = 1, …, n — the additives for p_k. As mentioned above, by Q_0j we denote the value of the j-th property, which the PC should possess.

After modifying the polymer p_k by adding s_ik its properties become equal Q_ikj, i = 1, …, n, k = 1, …, l, j = 1, …, m.

Further we get fuzzy numbers

u_ikj based on X_ikj = A(Q_ikj),

                                   u_0j based on X_0j = A(Q_0j),                                 (1)

where i = 1, …, n, k = 1, …, l, j = 1, …, m.

To select one additive and one polymer matrix we calculate

                                            n_ikj = u_0j( ),                                          (2)

where , i = 1, …, n, k = = 1, …, l,  j = 1, …, m and

                                         .                                       (3)

In the end, choose the additive  and polymer matrix , where .

4.2.  Computational experiment

We present a study of PC with alternative polymer matrices of polyurethane elastomer and polycaproamide and use a set of fire retardants presented in Table 5, for an extended demonstration of the capabilities of the fuzzy data analysis method. The number of flame retardants for simplicity of notation is the same as in the Table 2, but this is not essential for the method and, in general, the amount of additives for each polymer matrix can be different. In addition, the reference value, that is, additive number 0, is left the same as in Table 2. This is essential for the considered mathematical method of PC analysis.

Table 5: Background Characteristics of Fire Retardants for Elastomer Matrix [34]

Compound no., i	Qi1	Qi2	Qi3
0 (Reference,  q/d)	1.0/8	1.5/8.5	18/10
1	12.7	17.1	20
2	8.5	8.5	18
3	20.6	20.7	20
4	18.7	18.7	17
5	6.2	6.2	16
6	18.0	22.1	17
7	28.1	27.0	20
8	4.4	4.4	10

Let p₁ be polycaproamide, and p₂ — polyurethane elastomer, data on additives to which are given in Table 2 and Table 5 respectively. After the fuzzification of the initial data using (1), we obtain the fuzzy numbers u_i1j (Table 3) and u_i2j (Table 6) for p₁ and p₂, respectively.

Table 6: Parameters of Elements of the Matrix U(x) Calculated on the Data of Table 5

Compound no., i	qi1/δi1	qi2/δi2	qi3/δi3
0 (Reference,  q/d)	1.0/8	1.5/8.5	18/10
1	12.7/0.1	17.1/0.1	20/1
2	8.5/0.1	8.5/0.1	18/1
3	20.6/0.1	20.7/0.1	20/1
4	18.7/0.1	18.7/0.1	17/1
5	6.2/0.1	6.2/0.1	16/1
6	18.0/0.1	22.1/0.1	17/1
7	28.1/0.1	27.0/0.1	20/1
8	4.4/0.1	4.4/0.1	10/1

 Applying to the data Table 3 (k = 1) and Table 6 (k = 2) formula (2) we obtain the values n_ikj, i = 1, …, 8, k = 1, 2, j = 1, 2, 3. Next, using (3), we obtain n_ik, i = 1, …, 8, k = 1, 2, are given in Table 4 for k = 1 and in Table 7 for k = 2.

Table 7: Evaluation of Elastomer Fire Retardants in Compliance with Operational Requirements

Fire retardants no., i	νi2
1	0.45
2	0.71
3	0.35
4	0.34
5	0.81
6	0.33
7	0.34
8	0.77

Among the data Table 4 and Table 7 find the maximum value of 0.93, which corresponds to the addition of s₇₁ and the polymer matrix p₁.

Thus, a specific recommendation was received on the flame retardant, which is part of the PC. Extensive work is needed to formulate a recipe based on these recommendations. This, for example, the definition of other components or their part in the PC, which allows you to take the first step in developing a new PCM in an automated way. Here we note that the proposed analytical method also has the possibility of choosing additional components for PC design. This is covered below.

Above (see Table 1) we have already indicated that thanks to the growth and expansion of consumer requirements, the complexity of polymer systems are increasing simbatically. Therefore, identification tasks are also becoming more complex. Consider the complicated task of choosing several ingredients (additives) for PC design.

5. Selection of several additives for PC

5.1.  Method description

Let it be necessary to choose one polymer matrix from the set p_k, k = 1, …, l and r ≤ n additives for it from s_ik, i = 1, …, n.

To do this, we define r properties , …, , to improve which the choice of r additives is directed.

 For each polymer matrix p_k, we define a set of additives  (i_s Î {1, …, n}, s = 1, …, r, k = 1, …, l) such that the additive  provides the best property value among the additives s_1k, …, s_nk. However, some numbers may coincide with each other if the same additive provides the best values for several properties at once. In this case, for the modification, not r, but a correspondingly smaller amount of additives is used, but the result will correspond to the set task — the same r properties are improved.

Next, we obtain ν_ik, i = 1, …, n, k = 1, …, l as it was described in Section 4 and define

Determine the number

and choose a modification of the polymer matrix  a set of additives , …, .

5.2.  Computational experiment

To demonstrate the capabilities of the method presented here, we will use the same data (Table 2 and 5) and the same notation as above. Since the formulas for calculating the same, the values of ν_ik are also given in Table 4 and 7.

Table 8: Values of the Degree of Compliance of the Characteristics of Additives to Consumer Requirements to PCM

Compound no., i	k = 1			k = 2
	νi11	νi12	νi13	νi21	νi22	νi23
1	0.0625	0.349	0.438	0.235	0.102	0.994
2	0.0843	0.452	0.438	0.552	0,.632	0.950
3	0.0843	0.956	0.755	0.0173	0.0316	0.994
4	0.712	0.767	0.814	0.0365	0.0625	0.912
5	0.0843	0.998	0.438	0.752	0.813	0.867
6	0.966	0.979	0.480	0.0472	0.0187	0.912
7	1.0	0.987	0.814	0.000427	0.00226	0.994
8	1.0	0.999	0.5	0.885	0.924	0.5

Let r = 2, and j₁ = 1, j₂ = 2. To determine i₁ and i₂, ν_ikj values are needed that were not of immediate interest previously and were omitted from the examples of calculations. Now we bring these data to Table 8

To find i₁ for k = 1, we find the largest among the ν_i11 values. This is 1. This value is achieved for two supplements. We take i₁ = 7. Similarly, we get i₂ = 8. Acting in the same way, for k = 2 we define i₁ = 8, i₂ = 8.

Next, we calculate by (4)

ν₁ = α₁ν₇₁ + α₂ν₈₁ = 0.33·0.93 + 0.33·0.83 ≈ 0.58,

ν₂ = α₁ν₈₂ + α₂ν₈₂ = 0.33·0.77 + 0.33·0.77 ≈ 0.51.

The value ν₁ ≈ 0.58 indicates that for k = 1, the PC has a higher degree of compliance with the requirements. As a result, we choose a PC based on textile fiber (k = 1) with additives no. 7 and 8 (Table 2). Thus, a specific recommendation on the main additional component of the PC is also received here. The formation of a complete recipe based on these recommendations has the peculiarity that the proposed composition is already a multi-component system, but still has an incomplete character and requires more design and experimental work to implement the full “task-practice” algorithm. This, as well as noted above, can be the definition of additional components, their concentration in PC, technological and operating conditions. Calculations should be considered as a quantitative justification for the decision to develop a new PC. With the development of these approaches it is possible to create an automated system.

6. Conclusion

Summarizing the above, we note that often the CTS design problem arising at the initial stages is the task of choosing the best or, in a certain sense, optimal variant from the set of admissible ones. They must meet the specified requirements on the “composition – property – application” platform. When you try to get a solution in terms of incomplete and fuzzy information about the object of design, there is a high probability of incorrect or inaccurate multiple solutions. Therefore, the use of a clear strategy can minimize this probability, also reducing the cost of design and practical implementation of a technical solution.

The approach proposed in this article to mathematical modeling using fuzzy information in the field of chemical technology is essentially the mathematical support of a profiled IS. The formation of a database of models within the system allows us to bring the linguistic resources of the user interface to a new level of interaction using language environments more similar to natural languages and setting the input data in a form that is quite familiar to the researcher.

We should also note that only one of the most important aspects of using fuzzy simulation of PCM is shown here. It is aimed at using information in the form of fuzzy numbers when choosing PC components from a uniform set. As can be seen from the above results, the analysis of experimental data is well algorithmized and can be implemented as an IS of a chemist-researcher and a chemist-technologist. The above mathematical calculations are illustrated by the example of PCM design in general methodical terms, so they can be transferred to other natural and engineering systems in which multicomponentity is the main feature.

The development of the proposed computational methods creates theoretical foundations for the formalization and automation of the process of quality management of technical systems. In this case, it is possible to attract highly qualified experts only once to customize methods for solving specific tasks. The necessary step in this case is the formation of a library of settings and the solution of basic (“zero”) tasks. This will further allow you to work offline.

At the same time, the expert has several roles in stock:

• to identify the links between informal entities of the subject domain and formal entities of the theory of FS;
• the formation of an optimal set of requirements that a quality product must meet;
• applied to the PCM — selection of the PC composition according to the selected requirements.

This information will further allow to formalize the initial data of the subject area in terms of the theory of FS and use them in calculations, when upon receipt of an order from the consumer a set of requirements for PCM is automatically generated, and then estimates of formed requirements for specific candidates for PC components are calculated. Then a decision is made on the technical implementation of the composition, which ensures high quality of PCM. The analysis given here is given as a possible prospect for the development of the applied use of fuzzy mathematics tools in engineering. The stated essence of the method shows its role and value in solving the problem of quality management of PCM and other technical systems.

At the same time, we selectively point out the nearest additional applied work-analogues and areas in which methods for analyzing fuzzy information are being developed. These are economics [35], management systems [27], analysis of leasing projects [36], traffic optimization [37], occupational studies [38]. As a prospect, it can be viewed as technical compositions of medicinal and cosmetic forms, building and drilling mixtures and solutions, alloys, and some colloidal systems. As a nontrivial and nontechnical one, it is possible to propose to consider personnel recruitment tasks, for example, for diplomatic or other complex, for example, artistic work, from a certain number of applicants with a quantitative assessment of personal data and interview results. The basis for this is [39, 40]. True, the fully successful outcome of the future work of candidates cannot be guaranteed — one thing is a technique, the other is people-specialists. The risk factor, as in polymer and other systems, remains, but it is much higher.

Conflict of Interest

The authors declare no conflict of interest.

Acknowledgment

The reported research was funded by Russian Foundation for Basic Research and the government of Volgograd region, grant № 18-48-340011 “Quality management of polymer products based on the optimization of formulation of composite materials”

1.  I. V. Germashev, T. P. Mashihina, V. E. Derbisher, “Analysis of Fuzzy Data for Polymer Production Quality Management” in 2018 International Russian Automation Conference, RusAutoCon, Sochi Russia, 2018. https://doi.org/10.1109/RUSAUTOCON.2018.8501653
2.  J.-o. Kim, C. W. Mueller, Factor Analysis: Statistical Methods and Practical Issues, SAGE Publications, 1978. https://dx.doi.org/10.4135/9781412984256.
3.  Y. S. Vygodsky, T. V. Volkova, O. N. Zabegaeva, Z. Y. Chistyakova, V. A. Shanditsev, M. I. Buzin, Y. V. Zubavichus, O.V. Sinitsyna, G. G. Nikiforova, A. P. Krasnov et al., “Synthesis and characteristics of the composites based on poly(caproamide) and multiwalled carbon nanotubes” Polym. Sci. Ser. C+, 51(1), 63–73, 2009. https://doi.org/10.1134/S1811238209010111
4.  P. D. Shestakov, A. V. Galtsev, A. S. Tarasov, “Hardening Polymer Composites with Carbon Nanotubes” International Scientific Research Journal, 6(6), 79–81, 2012.
5.  M. G. Svistunov, V. E. Golovin, K. K. Koshelev, G. A. Kosheleva, Y. N. Nesterov, O. K. Barashkov, E`lektroizolyatsionnaya polimernaya kompozitsiya, Patent RU 2636383, 2017.
6.  W. R. Klecka, Discriminant Analysis, SAGE Publications, 1982. https://dx.doi.org/10.4135/9781412983938.
7.  M. S. Aldenderfer, R. K. Blashfield, Cluster Analysis, SAGE Publications, 1984. https://dx.doi.org/10.4135/9781412983648.
8.  A. Faure, Perception et Reconnaissance des Formes, Nombreux schémas N&B, 1985.
9.  A. G. Blokhnin, “Fuzzy-set algebra” J. Comput. Sys. Sc. Int+, 37(5), 747–754, 1998.
10.  M. G. Voskoglou, I. Y. Subbotin, “Application of the triangular fuzzy model to assessment of analogical reasoning skills” American Journal of Applied Mathematics and Statistics, 3(1), 1–6, 2015. https://doi.org/10.12691/ajams-3-1-1.
11.  D. Silva, L. F. V. Pinto, D. Bozukova, L. F. Santos, A. P. Serro, B. Saramago, “Chitosan/alginate based multilayers to control drug release from ophthalmic lens” Colloid Surface B, 147, 81–89, 2016. https://doi.org/10.1016/j.colsurfb.2016.07.047.
12.  T. Ikeda, H. Tamura, T. Sakurai, S. Seki, “Control of optical and electrical properties of nanosheets by the chemical structure of the turning point in a foldable polymer” Nanoscale, 8(30), 14673–14681, 2016. https://doi.org/10.1039/c6nr01066k.
13.  A. Kobayashi, T. Nakaza, T. Hirano, S. Kitagawa, H. Ohtani, “Variation in the chromatographic, material, and chemical characteristics of methacrylate-based polymer monoliths during photoinitiated low-temperature polymerization” J. Sep. Sci., 39(13), 2459–2465, 2016. https://doi.org/10.1002/jssc.201600344.
14.  B. Strachota, J. Hodan, L. Matejka, “Poly(N-isopropylacrylamide)-clay hydrogels: Control of mechanical properties and structure by the initiating conditions of polymerization” Eur. Polym. J., 77, 1–15, 2016. https://doi.org/10.1016/j.eurpolymj.2016.02.011.
15.  L. Y. T. Chou, F. Song, W. C. W. Chan, “Engineering the structure and properties of DNA-nanoparticle superstructures using polyvalent counterions” J. Am. Chem. Soc., 138(13), 4565–4572, 2016. https://doi.org/10.1021/jacs.6b00751.
16.  I. V. Germashev, V. E. Derbisher, T. M. Kokorina, I. A. Murashkina, “Assessing the quality of knitted fabrics using the theory of inexact sets” Izvestiya Vysshikh Uchebnykh Zavedenii, Seriya Teknologiya Tekstil’noi Promyshlennosti, (4), 7–10, 1999 (article in Russian with an abstract in English).
17.  V. E. Derbisher, I. V. Germashev, G. G. Bodrova, “Fuzzy-set-based quantitative estimates of the efficiency of thermo- and photostabilizing additives in polymeric compositions” Polym. Sci. Ser. A+, 39(6), 630–633, 1997.
18.  B. A. Khidhir, W. Al-Oqaiel, P. M. Kareem, “Prediction models by response surface methodology for turning operation” American Journal of Modeling and Optimization, 3(1), 1–6, 2015. https://doi.org/10.12691/ajmo-3-1-1.
19. M. R. S. Emami, “Fuzzy logic applications in chemical processes” The J. of Math. and Comput. Sci., 1(4), 339–348, 2010. https://doi.org/10.22436/jmcs.001.04.11.
20.  S. Krishnamoorthy, “Linguistic features for review helpfulness prediction” Expert Syst. Appl., 42(7), 3751–3759, 2015. https://doi.org/10.1016/j.eswa.2014.12.044.
21.  K. Nasrollahzadeh, M. M. Basiri, “Prediction of shear strength of FRP reinforced concrete beams using fuzzy inference system” Expert Syst. Appl., 41(4), 1006–1020, 2014. https://doi.org/10.1016/j.eswa.2013.07.045.
22.  A. Salski, F. Bartels, “A fuzzy approach to land evaluation” IASME Trans., 5(2), 774–780, 2005.
23.  M. I. Kizhisseri, M. M. A. Mohamed, “Fuzzy-based wastewater quality indices for pollution classification: a case study in the United Arab Emirates” Environment Systems and Decisions, 36(1), 62–71, 2016. https://doi.org/10.1007/s10669-015-9579-9.
24.  P. H. Chandra, S. M. S. T. Kalavathy, A. M. I. Jayaseeli, J. P. Karoline, “Mechanism of fuzzy ARMS on chemical reaction” in V. Snášel, A. Abraham, P. Krömer, M. Pant, A. Muda (eds) Innovations in Bio-Inspired Computing and Applications. Advances in Intelligent Systems and Computing, 424, 43–53, 2016. https://dx.doi.org/10.1007/978-3-319-28031-8_4.
25.  I. V. Germashev, V. E. Derbisher, T. F. Morozenko, S. A. Orlova, “Otsenka kachestva tehnicheskih ob”ektov s ispol`zovaniem nechyotkih mnozhestv” Industrial laboratory. Diagnostics of materials, 67(1), 65–68, 2001.
26.  I. V. Germashev, V. E. Derbisher, “Fuzzy Optimization of Polymer Compositions” Theor. Found. Chem. Eng., 35(4), 418–421, 2001.
27.  A. A. Uskov, I. A. Kiselev, “Comparing fuzzy arithmetic with quaternion arithmetic and applying the former to control system analysis” Large-scale Systems Control, (48), 59–70, 2014 (article in Russian with an abstract in English).
28.  A. I. Orlov, E. V. Lutsenko, Sistemnaya Nechyotkaya Interval`naya Matematika, KubGAU, 2014.
29.  A. I. Orlov, Nechislovaya Statistika, MZ-Press, 2004.
30.  E. Egrioglu, C. H. Aladag, M. A. Basaran, U. Yolcu, V. R. Uslu, “A new approach based on the optimization of the length of intervals in fuzzy time series” J. Intell. Fuzzy Syst., 22(1), 15–19, 2011.
31.  I. V. Germashev, V. E. Derbisher, E. V. Derbisher, E. A. Markushevskaya, “The Fuzzy Data Analysis for the Chemical-Technological Systems Optimization” Information Technologies, 24(3), 153–160, 2018 (article in Russian with an abstract in English).
32.  V. P. Meshalkin, E`kspertny`e Sistemy` v Himicheskoy Tehnologii, Chemistry, 1995.
33.  I. V. Germashev, V. E. Derbisher, “Properties of unimodal membership functions in operations with fuzzy sets” Russian Mathematics, 51(3), 72–75, 2007. https://doi.org/10.3103/S1066369X07030115.
34.  I. V. Germashev, V. E. Derbisher, S. A. Orlova, “Evaluation of activity of the fireproofing compounds in elastomer compositions by means of fuzzy sets” Kauchuk i Rezina, (6), 15–17, 2001 (article in Russian with an abstract in English).
35.  Y. I. Davydov, “Primenenie teorii nechyotkih mnozhestv k e`konomicheskim zadacham” News of St. Petersburg State Agrarian University, (26), 261–266, 2012.
36.  Y. I. Davydov, “Teoriya nechyotkih mnozhestv v otsenke e`konomicheskoy e`ffektivnosti lizingovy`h proektov v usloviyax neopredelennosti i riska” News of the International Academy of Agrarian Education, (14-2), 32–39, 2012.
37.  V. A. Romanenko, “Fuzzy optimizing of transfer air transportation system parameters” Bulletin of the Samara State Technical University, Series: Technical Sciences, (4), 73–80, 2012 (article in Russian with an abstract in English).
38.  G. A. Kryzhanovsky, V. V. Kupin, “Analiz vazhnosti professional`ny`h zadach na osnove nechetkih chislovy`h e`kspertny`h otsenok” Bulletin of St. Petersburg State University of Civil Aviation, (2), 43–50, 2012.
39.  S. V. Skorokhod, “Otbor personala v usloviyah nechyotkoy informatsii na osnove e`kspertny`h otsenok” News of SFU. Engineering Science, (9), 125–130, 2008.
40.  S. V. Skorokhod, “Primenenie nechyotkih chisel dlya otsenki kvalifikatsii personala” News of TRTU, (3), 214–216, 2005.

(Click Here)

(Click Here)