1. Introduction

At the invitation of the associate editors of the Advances in Science, Technology and Engineering Systems Journal (ASTESJ), the author presents the following manuscript on an in-depth theoretical expansion of a conference paper previously submitted in the Applied Computational Electromagnetics Society (ACES) Symposium proceedings in 2018 [1].  Originally, the author only discussed the explanation of the suppression effect of anisotropic birefringence inside a rectangular waveguide in brief, and the author feels that scientific interest in the subject warrants a more in depth theoretical examination of the phenomenon.  The author has also presented other portions of the theory relating to anisotropic wave propagation in a second publication [2].  Therefore, the author is happy to contribute an expansion on this aspect of the anisotropic birefringence theory to a special issue of ASTESJ at the invite of the associate editors.  The article will focus on how the derivation of the anisotropic wave equation in a biaxial anisotropic medium leads to birefringence through a fourth order dispersion equation.  The final section will explain how constraints on the boundary conditions of modes in rectangular waveguides can negate the effect of birefringence.

 Scientists have understood electromagnetic wave propagation in homogeneous anisotropic optical media since the 1950s. At optical frequencies, one has to rely on naturally occurring crystalline media with anisotropic properties. However, as early as 1958 Collin showed that at microwave frequencies, where the wavelength is much greater, it is possible to fabricate artificial dielectric media having anisotropic properties [3].

Recently engineered materials have come to play a dominant role in the design and implementation of electromagnetic devices and especially antennas.  Metamaterials, MetaFerrites, and magneto-dielectrics have all come to play a crucial role in advances made in both the functionality and characterization of such devices.  In fact, a movement towards utilizing customized material properties to replace the functionality of traditional radio frequency (RF) components such as broadband matching circuitry, ground planes, and directive elements is apparent in the literature and not just replacement of traditional substrates and superstrates with engineered structures.  A firm theoretical understanding of the electromagnetic properties of these materials is necessary for both design and simulation of new and improved RF devices.

Inherently, some of these engineered materials have anisotropic properties.  Previously, the study of anisotropy had been limited mostly to the realm of optical frequencies where the phenomenon occurs naturally in substances such as liquid crystals and plasmas.  However, the recent development of a separate class engineered materials at microwave frequencies has encouraged the study of electromagnetic anisotropy for RF applications.  Low loss anisotropic magneto-dielectrics greatly expands the current antenna design space.  Anisotropic media provide unique properties not available using isotropic media.  These include a high effective refractive index reducing the electrical size of wavelengths in a medium, relatively low magnetic loss at MHz frequencies, and lower density and weight than traditional isotropic ferrite materials.  Anisotropic media can be up to five times less dense than traditional ferrites while exhibiting magnetic properties with lower loss tangents.  Relevant work in this area includes plane wave solutions to propagation in anisotropic media [4-6].  Researchers have also performed modal decomposition of rectangular waveguides filled with anisotropic magneto-dielectrics along with in depth analysis of cut-off wave numbers and field distributions [7, 8].

An anisotropic electromagnetic medium defines permittivity (ε_r) and permeability (µ_r) as separate tensors where the values differ in all three Cartesian directions (ε_x≠ε_y≠ε_z and µ_x≠µ_y≠µ_z).  This is known as the biaxial definition of anisotropic material which is more encompassing than the uniaxial definition which makes the simplifying assumption that ε_x=ε_y=ε_t and µ_x=µ_y=µ_t.  The anisotropic definition also differs from the traditional isotropic definition where ε_r and µ_r are the same in all three Cartesian directions defined by a single value.  Anisotropic media yield characteristics such as conformal surfaces, the focusing and refraction of electromagnetic waves as they propagate through a medium, high impedance surfaces for artificial magnetic conductors as well as high index, low loss, and lightweight ferrite materials.  The following sections aim to discuss in more detail some RF applications directly affected by the incorporation of anisotropic media and will also present a rigorous derivation of the wave equation and dispersion relationships for anisotropic magneto-dielectric media.  All results agree with those presented by Meng, et. al [7, 8].  Furthermore, setting m_r = I, where I is the identity matrix, yields results that agree with those presented by Pozar and Graham for anisotropic dielectric media [6, 9].

2. Applications of Anisotropy in Radio Frequency (RF) Devices

Traditionally, the study of anisotropic properties for RF was limited to a narrow application space where traditional ferrites exhibiting natural anisotropy were the enabling technology.  These types of applications included isolators, absorbers, circulators and phase shifters [10, 11].  Traditional ferrites are generally very heavy and very lossy at microwave frequencies and those are the two main limiting factors narrowing their use in RF devices; however, propagation loss is an important asset to devices such as absorbers.  Anisotropy itself leads to propagation of an electromagnetic wave in different directions. This phenomenon is already important in devices such as circulators and isolators [10].  For phase shifters and other control devices, changing the bias field across the ferrite controls the microwave signal [11].  However, newer versions of some of these devices, utilizing FETs and diodes in the case of phase shifters, rely on isotropic media to enable higher efficiency devices.

As early as 1958, Collin showed that at microwave frequencies, where the wavelength is larger, it is possible to fabricate artificial dielectric media having anisotropic properties [3].  This has led some to investigate known theoretical solutions to typical RF problems, such as a microstrip patch antenna, and extend them utilizing anisotropic wave propagation in dielectric media [5, 6].  The anisotropic dielectric antenna shows interesting features of basic antenna applications featuring anisotropic substrates.  While these solutions establish a framework for electromagnetic wave propagation in anisotropic media, they simplify the problem by necessarily setting µ_r=1 and only focusing on dielectric phenomena of anisotropy.

The proliferation of metamaterials research over the last few decades exemplifies the growing interest in the area of artificial media [12-22].  Metamaterials incorporate the use of artificial microstructures made of subwavelength inclusions implemented with periodic and/or multilayered structures known as unit cells [13]. These devices operate where the wavelength is much larger than the characteristic dimensions of the unit cell elements. One characteristic feature of some types of metamaterials is wave propagation anisotropy [14].  Applications such as directive lensing [15], cloaking [16], electronic beam steering [17], metasurfaces [18], anisotropic oscillators [19], and optics [20] among others all utilize anisotropic media as the enabling technology.  More recent research focuses on the proper modeling schemes for computational electromagnetics [21] or examining phenomenon such as scattering off of anisotropic objects [22].

A class of engineered materials exists, known as MetaFerrites, that exhibits positive refractive index, anisotropy, and magneto-dielectric properties with reduced propagation loss at microwave frequencies compared to traditional ferrites.  These materials show the unique ability to provide broadband impedance matches for very low profile antennas by exploiting the inherent anisotropy to redirect surface waves thus improving the impedance match of the antenna when very close to a ground plane.  Designers have demonstrated antenna profiles at 200 MHz to 500 MHz on the orders of a fortieth of a wavelength using these anisotropic media with over an octave of bandwidth and positive realized gain [2, 23].

3. Anisotropic Wave Equation

The recent development of low loss anisotropic magneto-dielectrics greatly expands the current antenna design space.  Here we present a rigorous derivation of the wave equation and dispersion relationships for anisotropic magneto-dielectric media.  All results agree with those presented by Meng, et. al [7, 8].  Furthermore, setting m_r = I, where I is the identity matrix, yields results that agree with those presented by Pozar and Graham for anisotropic dielectric media [6, 9]. Incorporating a fully developed derivation of anisotropic properties of both ε_r and µ_r expands upon the simplification imposed by both Pozar and Graham that uses an isotropic value of µ_r=1.  An expansion on the results of Meng, et. al given in section 4 develops the waveguide theory including a full modal decomposition utilizing the biaxial definition of anisotropy versus their simplified uniaxial definition.  The derivation of anisotropic rectangular waveguide resonance in section 6 differs from that of Meng, et. al by addressing the direct relationship between boundary conditions and the existence of birefringence.  Furthermore, the analysis of anisotropic properties is not restricted to double negative materials, which is the case for the Meng, et. al studies.

In order to solve for the propagation constants we will need to formulate the dispersion relationship from the anisotropic wave equation.  This allows us to solve for the propagation constant in the normal direction of the anisotropic medium.  We start with the anisotropic, time harmonic form of Maxwell’s source free equations for the electric and magnetic fields

where w is the frequency in radians, e_o is the permittivity of free space, m_o is the permeability of free space, E=x_oE_x+y_oE_y+z_oE_z, and H=x_oH_x+y_oH_y+z_oH_z.  We define m_r and e_r as

Using the radiation condition, we assume a solution of E(r)=E(x,y)exp(-jk_zz).  Now isolate the individual components of (5) by taking the dot product with x_o, y_o, and z_o respectively.  This operation yields the following equations

Now that we have relationships for the transverse field components, we can solve (1) and (2) for H and E respectively

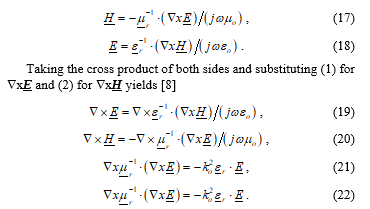Equations (21) and (22) represent the vector wave equations in an anisotropic medium.

4. Dispersion Equation for H_z

We expand the ÑxH term of (22) in terms of (13-16), and take the dot product with e_r^-1

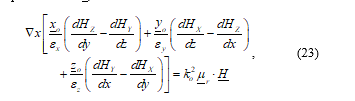Evaluating (23) and taking the dot product with the z_o direction allows us to isolate the H_z component of the magnetic field on the right hand side of the equation

Setting E_z=0, if we differentiate (13) by d²/dxdz and (14) by d²/dydz, keeping in mind that d/dz = –jk_z, we arrive at the following result

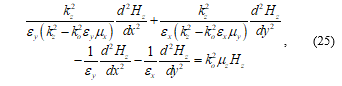Combining the d²H_z/dx² and d²H_z/dy² terms in (25) gives the following second order differential dispersion equation for H_z

5. Dispersion Equation for E_z

We expand the ÑxE term of (21) in terms of (13-16), and take the dot product with m_r^-1

Evaluating (27) and taking the dot product with the z_o direction allows us to isolate the E_z component of the magnetic field on the right hand side of the equation

Setting H_z=0, if we differentiate (15) by d²/dxdz and (16) by d²/dydz, keeping in mind that d/dz = –jk_z, and plug the results into (28), then we arrive at the following result

Combining the d²E_z/dx² and d²E_z/dy² terms in (38) gives the following second order differential dispersion equation for E_z

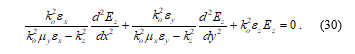6. Suppression of Birefringence in a Rectangular Waveguide

Birefringence is a characteristic of anisotropic media where a single incident wave entering the boundary of an anisotropic medium gives rise to two refracted waves as shown in Figure 1 or a single incident wave leaving gives rise to two reflected waves as shown in Figure 2. We call these two waves the ordinary wave and the extraordinary wave. For low order modes, and especially the first mode, a rectangular waveguide suppresses the birefringence inherent to anisotropic media by suppressing propagation in the vertical direction.  This suppression assumes that the dimensions of the waveguide are such that the horizontal dimension is at least twice the size of the vertical dimension [10].  To see how the geometry of the waveguide acts to cancel out the extraordinary wave, we need to solve for k_z from our dispersion equations.

Equations (26) and (30) yield the following solutions in unbounded anisotropic media restricted by the radiation condition (previously stated in section 3)

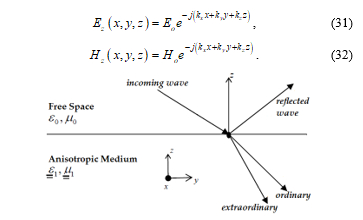Figure 1:  Free space plane wave incident on an anisotropic boundary [9].

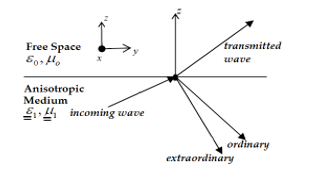Figure 2:  Anisotropic plane wave incident on a free space boundary [9].

Plugging (31) into (30) (equivalently we could substitute (32) into (26)) yields a polynomial equation whose solutions give the values of k_z in the anisotropic medium.  Noting that d²/dx² = –k_x² and d²/dy² = –k_y², (30) simplifies to

Dividing out the term and multiplying through by both denominators gives us the following factored polynomial

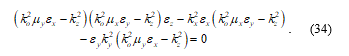Finally, multiplying out (34) yields a fourth order polynomial whose roots yield the four values of k_z describing the ordinary wave and extraordinary wave in the positive and negative propagation directions

Equation (35) is directly responsible for the existence of the two ordinary and extraordinary waves that are characteristic of the birefringence phenomenon.  In an isotropic medium, the resulting polynomial for k_z is a second order polynomial, which yields only the values for the positive and negative propagation of the single ordinary wave.  A fourth order polynomial allows for positive and negative propagation of both the ordinary and extraordinary wave shown in Figures 1 and 2.

The suppression of birefringence requires (35) to reduce to a second order polynomial.  This is clearly not possible in an unbounded anisotropic medium as currently formulated.  However, the boundary conditions in a rectangular waveguide assume that the first resonance suppresses the propagation constant in the vertical direction [10].  In other words, k_y=0 and d²/dy²=0, and this completely eliminates the second E_z term in (33).  This simplifies (34) to

which resembles the form of the traditional second order wave equation.  Solving for k_z thus leads to the following second order polynomial

Since (37) yields the positive and negative square root of the right-hand-side as the two solutions for k_z, this indicates the existence of only a single propagating wave.  The suppression of the k_y term in the first resonant mode of the rectangular waveguide yields a second order differential equation for the wave number in the propagation direction, thereby eliminating the property of birefringence for this case.   For a practical validation of this theory, the author would point the reader to reference [2].  This paper shows an antenna application that exploits the suppression of anisotropic birefringence to facilitate wideband impedance matching of a cavity backed antenna.

The reader should remember that (37) applies only to the first order resonance mode of the rectangular waveguide.  As higher order modes are introduced propagation birefringence will exist for some modes depending on the boundary conditions. A similar analysis should be carried out for each propagating mode.

Conflict of Interest

The authors declare no conflict of interest.

1.  G. Mitchell, “Suppression of anisotropic birefringence in a rectangular waveguide” in Proceedings of the Applied Computational Electromagnetics Society (ACES) Symposium, 2018.
   https://doi.org/10.23919/ROPACES.2018.8364258
2.  G. Mitchell and W. Wasylkiwskyj, “Theoretical anisotropic transverse resonance technique for the design of low profile wideband antennas” IET Microwaves, Antennas and Propagation, 10(5), 487-493, 2016. https://doi.org/10.1049/iet-map.2015.0470
3.  R. Collin, “A Simple Artificial Anisotropic Medium” IRE Transactions on Microwave Theory and Techniques, 6(4), 206-209, 1958. https://doi.org/10.1109/TMTT.1958.1125216
4.  M. Pardavi-Horvath, “Microwave Applications of Soft Ferrites” Journal of Magnetism and Magnetic Materials, 215-216(1), 171-183, 2000. https://doi.org/10.1016/S0304-8853(00)00106-2
5.  K. Buell, H. Mosallaei, K. Sarabandi, “A Substrate for Small Patch Antennas Providing Tunable Miniaturization Factors” IEEE Transactions on Microwave Theory and Techniques, 54(1), 135-146, 2006. https://doi.org/10.1109/TMTT.2005.860329
6.  D. Pozar, “Radiation and Scattering from a Microstrip Patch on a Uniaxial Substrate” IEEE Transactions on Antennas and Propagation, 35(6), 613-621, 1987. https://doi.org/10.1109/TAP.1987.1144161
7.  F.Y. Meng, Q. Wu, L. W. Li, “Transmission Characteristics of Wave Modes in a Rectangular Waveguide filled with Anisotropic Metamaterial” Applied Physics A: Materials Science and Processing, 94(4), 747-753, 2009. https://doi.org/10.1007/s00339-008-5057-2
8.  F.Y. Meng, Q. Wu, J.H. Fu, “Miniaturized Rectangular Cavity Resonator based on Anisotropic Metamaterials Bilayer” Microwave and Optical Technology Letters, 50(8), 2016-2020, 2008. https://doi.org/10.1002/mop.23556
9.  J. Graham, “Arbitrarily Oriented Biaxially Anisotropic Media: Wave Behavior and Microstrip Antennas,” Ph.D Thesis, Syracuse University, 2012.
10.  D. Pozar, Microwave Engineering: 3rd edition, John Wiley and Sons, 2005.
11.  W.J. Ince, E. Stern, “Non-Reciprocal Remanence Phase Shifters in Rectangular Waveguide” IEEE Transactions on Microwave Theory and Techniques. 15(2), 87-95, 1967.
    https://doi.org/10.1109/TMTT.1967.1126381
12.  D. Torrent, J. Sanchez-Dehesa, “Radial Wave Crystals: Radially Periodic Structures from Anisotropic Metamaterials for Engineering Acoustic or Electromagnetic Waves” Physics Review Letters, 103(6), 2009. https://doi.org/10.1103/PhysRevLett.103.064301
13.  J. Sanchez-Dehesa, D. Torrent, J. Carbonell, “Anisotropic metamaterials as sensing devices in acoustics and electromagnetism” in Proceedings of the International Society for Optics and Photonics (SPIE), 2012. https://doi.org/10.1117/12.916043
14.  Y.G Ma, P. Wang, X. Chen, C.K. Ong, “Near-field plane-wave-like beam emitting antenna fabricated by anisotropic metamaterial” Applied Physics Letters, 94(4), 2009. https://doi.org/10.1063/1.3077128
15.  Q. Cheng, “Directive Radiation of Electromagnetic Waves Based on Anisotropic Metamaterials” in Proceedings of IEEE Asia-Pacific Conference on Antennas and Propagation, Singapore, Singapore, 2012.
16.  D. Schurig, J. Mock, B. Justice, S. Cummer, J. Pendry, A. Starr, D. Smith, “Metamaterial electromagnetic cloak at microwave frequencies” Science, 314(5801), 977-980, 2006. https://doi.org/10.1126/science.1133628
17.  J. Wong, K. Balmain, “A beam-steerable antenna based on the spatial filtering property of hyperbolically anisotropic metamaterials” in Proceedings of IEEE International Symposium of the Antennas and Propagation Society, Honolulu, HI, USA, 2007. https://doi.org/10.1109/APS.2007.4396438
18.  T. Cai, G.M. Wang, “Polarization-controlled Bifunctional Antenna based on 2-D Anisotropic Gradient Metasurface” in Proceedings of IEEE Conference on Microwave and Millimeter Wave Technology, Beijing, China, 2016. https://doi.org/10.1109/ICMMT.2016.7761687
19.  W. Zhong, X. Meng, Q. Hong, “Radiation power of half wave oscillator antenna in magnetic anisotropic medium” in 2018 International Conference on Electronics Technology (ICET), Chengdu, China, 2018.
    https://doi.org/10.1109/ELTECH.2018.8401446
20.  M. Born, E. Wolf, Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light: 7th edition, Cambridge University Press, 1999.
21.  O. Ozgun, M. Kuzuoglu, “Finite element modeling of anisotropic half-space problems by a simple mesh truncation scheme” in 2017 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, San Diego, CA, USA 2017.
    https://doi.org/10.1109/APUSNCURSINRSM.2017.807283
22.  J. Zhuo, F. Han, L. Ye, Z. Yu, Q.H. Liu, “Simulation of Electromagnetic Scattering of 3-D Inhomogeneous Biaxial Anisotropic Magnetodielectric Objects Embedded in Uniaxial Anisotropic Media by the Mixed-Order BCGS-FFT Method” IEEE Transactions on Microwave Theory and Techniques, 66(8), 3745-3755, 2018.
    https://doi.org/10.1109/TMTT.2018.2840984
23.  G. Mitchell, S. Weiss, “An Overview of ARL’s Low Profile Antenna Work utilizing Anisotropic MetaFerrites”, in Proceedings of the IEEE International Symposium on Phased Array Systems and Technology, Waltham, MA, USA, 2016. https://doi.org/10.1109/ARRAY.2016.7832581

(Click Here)

(Click Here)