1. Introduction

This paper is an extension of work originally presented in 2018 IEEE International Conference” Management of Municipal Waste as an Important Factor of Sustainable Urban Development” (WASTE). The influence of flame propagation as a result of heat losses from the reaction zone is the main factor of ensuring explosion safety for combustible gas systems. Thermal losses make it impossible to spread the flame beyond certain boundaries of composition and instrumental conditions. The mechanism of thermal losses plays a leading role in solving the emerging problems of explosion safety. The objective is to provide a general introduction to the Mechanics of heat transfer, together with its elementary applications to Solid and Fluid Mechanics. As result it would assimilated the principal concepts and laws governing the kinematics and dynamics of deformable media. In addition, this research should understand the application of this theory to the cases (i) of infinitesimal Thermo-Elasticity, and (ii) of Newtonian and perfect Fluid Mechanics [1-4].

2. Description of Problem

Mathematical and computer modeling provided a medium of exchange for the diverse disciplines (Mechanics and IT) utilizing mathematical or computer modeling as either a theoretical or working tool. Equal attention was given to the mechanics, methodology and theory of modeling with an attempt to advocate either mathematical or computer modeling, or a combination of the two, in an integrative form [5-7]. When burning in a narrow channel, the key to the mechanism of thermal losses from the reaction zone is the conductive heat conductivity to the walls of the channel. In this case, the reaction zone of obviously explosive gas systems is cooled. In sufficiently narrow channels, heat loss is possible, leading to quenching even of the most rapid-blowing known explosive systems. This feature combustion in narrow channels used in flame arrestors with narrow channels separating apparatus in which possible initiation foci combustion fire-retardant protected by the surrounding space, filled with a potentially explosive environment. The gas and flame have no other way out of the dangerous apparatus.

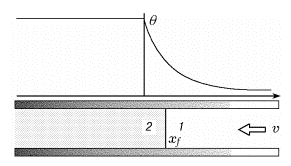Figure 1:  Flame attenuation in narrow channels

The Figure 1 shows a diagram of a flame in a flat channel. As in the classical formulation, approximations are used about the constant density, heat capacity, and thermal conductivity of the gas.

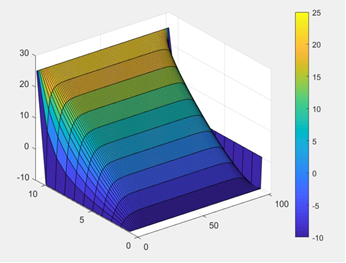 Figure. 2: Temperature distribution from wall to center of channel

This Figure 2 represents the temperature distribution from wall to center of channel. Identifying the relevant heat transfer processes on a heating when the foamed insulation sheet of channel is placed on inner surface and on the outer surface of channel. To avoid singular solution, the round configuration of channel is preferred.

3. Flame attenuation, mathematical modeling

Processes with heat regeneration include filtration combustion of gases, where the flame can stabilize in microchannels between the solid phases, even if the dimensions of the microchannels are substantially smaller than the critical diameter determined from the initial temperature. Combustion in this case is possible provided that the gas phase is surrounded by walls with a temperature exceeding the ambient temperature. This work can be considered as a continuation of the classical works on flame propagation taking into account the transfer of heat from the combustion products to the fresh mixture by an inert medium due to its high thermal conductivity.

Combustion of gas in a channel with heat exchange is the simplest example of a system with a convective heat recovery method. A characteristic feature of combustion in such a system is the thermal interaction between the combustion products and the fresh mixture through the heat-conducting wall. In this linear configuration, unlike devices with special combustion chambers, the flame stabilizes inside the inlet tube. This mechanism of flame stabilization is typical for small-sized systems with recirculation of heat. Studies of the dynamic behavior of a flame in a system with counter-current heat transfer make it possible to study the characteristics of combustion in systems with heat recovery, and also covers a whole series of new phenomena.

It is necessary to solve the Cauchy problem for the one-dimensional heat equation (a second-order partial differential equation that describes the temperature distribution in a given region of space and its variation over time) using parallel programming tools. The problem is solved for a homogeneous heat equation (the system is insulated) on the interval [0, L]: One-dimensional dimensionless equations for temperature have the form

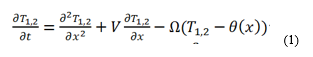Here the dimensionless time t is measured in units of correlation between thermal properties of gas in channel and adiabatic velocity of gas, i.e. æ/Vb², the dimensionless spatial coordinate x is in units of æ/Vb, where æ is the thermal diffusivity of the gas, and Vb is the adiabatic velocity of the flat flame. The channel wall temperature θ and the gas temperature T are measured in terms of the adiabatic flame temperature Tb [8-10].

The subscripts 1 and 2 refer to the fresh mixture and combustion products, respectively. The gas velocity V is measured in units of Vb. The dimensionless heat transfer parameter Ω = 4Nu/Pe² is related to the Nusselt number Nu=αdₒ/λg and the Peclet number Pe=Vbdₒ/æ, which are determined for the channel of height dₒ (here α is the heat transfer coefficient; λg is the thermal conductivity of the gas). The boundary conditions for equations (1) far from the flame have the following form:

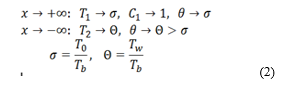 where T0 is the initial temperature of the fresh mixture, Tw is the wall temperature at the hot end of the channel.

Thus, Equation (1) together with boundary conditions (2) at the ends of a narrow channel determines the spread of the flame in the channel. In this case, the temperature distribution in the channel is calculated (the flame temperature of the combustible gas and its mixture before and after mixing, the temperature of the channel walls and their combination are taken into account) as a function of time. Also, the differential equation of the second order includes the velocities and accelerations of the temperature change. The gas characteristics were calculated from some physical parameters: thermal diffusivity of the gas, dimensionless heat transfer parameter (as correlation of numbers of Nusselt and Peclet), heat transfer coefficient; the thermal conductivity of the gas. Thus, taking into account the boundary conditions (2), the boundary value problem was modeled and coded in Matlab.

4. Numerical calculations in MatLab

The numerical realization of heat transfer process was implemented in MatLab, and Adomian Decomposition Method was used for calculation of components of displacement of parts of fire extinguishing powders and burning reagents. This calculation needs to use some special functions for discretization of components of temperature.

% variable definition

Nx = 11;

Ny = 101;

X = 1.0;

Y = 10.0;

dx = X / (Nx – 1);

dy = Y / (Ny – 1);

dt = 1e-4;

% matrix definition

% initializing temperature in our  fire extinguishing and explosion suppression compositions

U1 = ones(Nx, Ny) * (-10);

U2 = ones(Nx, Ny) * (-10);

U3 = ones(Nx, Ny) * (-10);

% initializing temperature on right border in our fire extinguishing and explosion suppression compositions

for j=1:Ny + 1

  U1(Nx, j) = 25;

  U2(Nx, j) = 25;

  U3(Nx, j) = 25;

end

% loop till it converges

while 1

%     Using Adomian Decomposition Method to solve this eq

    A = 1 / (dx * dx);

    B = – (1 / dt + 2 / (dx * dx));

    C = 1 / (dx * dx);

    gamma = zeros(Nx);

    beta = ones(Nx) * (-10);

%     First loop using the definition temperature by X axis

    for j=2:Ny – 1

        for i=2:Nx

            F = -(discretize(U1, “y”, i, j) + U1(i, j) / dt);

            temp_div = B + C * gamma(i);

            beta(i + 1) = (F – C * beta(i)) / temp_div;

            gamma(i + 1) = -A / temp_div;

        end

%         U2(Nx, j) = – beta(j) / (1 – gamma(j));

        for i=Nx:-1:2

            U2(i – 1, j) = gamma(i) * U2(i, j) + beta(i);

        end

    end

    gamma = zeros(Nx);

    beta = ones(Nx) * (-10);

    A = 1 / (dy * dy);

    B = – (1 / dt + 2 / (dy * dy));

    C = 1 / (dy * dy);

%     Second loop using of temperature by Y axis

    for i=2:Nx – 1

        for j=2:Ny

            F = -(discretize(U2, “x”, i, j) + U2(i, j) / dt);

            temp_div = B + C * gamma(j);

            beta(j + 1) = (F – C * beta(j)) / temp_div;

            gamma(j + 1) = -A / temp_div;

        end

        for j=Ny:-1:2

            U3(i, j – 1) = gamma(j) * U3(i, j) + beta(j);

        end

    end

%     for j=Ny:-1:2

%         U3(Nx – 1, j) = U3(Nx – 2, j);

%     end

% And after every iteration check for convergence

    if converge(U1, U3)

        break;

    end

% In the end of every iteration – definition of new layer as old, and continuation till difference between them become less than epsilon

    U1 = U3;

    surf(U3)

end

% Plot surface to image easier the result

surf(U3)

colorbar

U3((Nx – 1) / 2, (Ny – 1) / 2)

% This function checks for convergence

function result = converge (U1, U2)

% Initial max difference is -1, because of it less than 0, and as we know

% absolute value of difference never be less than 0

max_diff = -1;

% My error rate (Epsilon)

eps = 1e-4;

Nx = 11;

Ny = 101;

% This loop gets max difference Between old and new layers

for i=1:Nx

    for j=1:Ny + 1

        if abs(U1(i, j) – U2(i, j)) > max_diff

            max_diff = abs(U1(i, j) – U2(i, j));

        end

    end

end

% As the result we get Boolean value

result = eps > max_diff;

end

% This function helps me make code easier to understand

function result = discretize (U, axis, i, j)

Nx = 11;

Ny = 101;

X = 1.0;

Y = 10.0;

dx = X / (Nx – 1);

dy = Y / (Ny – 1);

if axis == “x”

    result = (U(i + 1, j) – 2 * U(i, j) + U(i – 1, j)) / (dx * dx);

else

    result = (U(i, j + 1) – 2 * U(i, j) + U(i, j – 1)) / (dy * dy);

end

end

The basic mechanisms of combustion of gases in systems with heat recirculation can be clarified from the study of combustion of gases in a narrow channel with a controlled wall temperature. Therefore, studies of gas combustion in micro-channels with controlled wall temperature are necessary for understanding processes in both microsystems with heat regeneration, where the heating of the combustible mixture of gases occurs due to the heat of the exhaust combustion products, and for the development of new technologies that use combustion of gases in various media. The small dimensions of the channel in which combustion occurs allow the creation of an almost uniform temperature distribution in the cross section. Experiments show that the temperature gradient in the walls of the channel, which was created by an external heat source, remains practically constant, both with the combustion of gas inside the channel and without burning. These observations make it promising to use a microchannel with a temperature gradient to study the structure of the flame and to test existing models with detailed kinetics of chemical reactions.

Burning studies usually consider gas flows in which transport phenomena and chemical reactions play an important role. In order to analyze the combustion process, in addition to the chemical transformations of the substance, it is necessary to take into account the phenomena caused by the release of heat. If we take into account the interconnectedness of the above processes, then the complexity of the theoretical analysis of combustion becomes obvious.

Advances in the theory of combustion of gases were associated, first of all, with the use of simple and at the same time realistic mathematical models.

Software Package of given formulas are special calculations that can contain class folders, function, and class definition files, and other packages. The names of classes and functions in Matlab are scoped to the package folder. A package with name” TED in channels” (Thermoelastodynamics in channels) is unique. Function and class names must be unique only within the package. Using a package provides a means to organize classes and functions. Packages also enable you to reuse the names of classes and functions in different packages.

The proposed code of the software product allows you to transparently change the approaches to calculation, change the parameters to be set. Explicit schemes for solving the differential equation are proposed. Also in Matlab, visualization of the computational process was carried out.

The Graphical User Interface GNUI requires the following parameters:

• Diameter of channel (in m),
• Velocity of motion gas or fluid (in m/sec),
• Length of channel (in m).

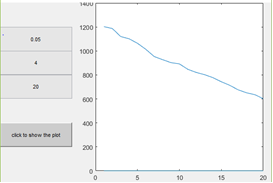Figure 3: Visualization of flame attenuation in narrow channels in TED in channels

Figure 3 represents the Interface of package and input/output parameters. The graph of the dependence of the change in the combustion temperature of methane on the length of a narrow channel clearly indicates a decrease in temperature during motion away from the flame front, which confirms the physical nature of the problem and the correctness of the chosen mathematical model.

Thus, a mathematical model of flame burning in a narrow channel has been developed, the properties of burning and quenching of gas or liquid in a narrow channel have been studied, depending on the combustion temperature and the flame propagation velocity in the channel. In this case, the inhibitory properties of the substance, flame propagation in thin channels are investigated [11-13]. Based on the 2-D model, a computer model was created in MatLab14. This model requires the specification of some input parameters and provides a graphical representation of the temperature dependence of the length of the channel. The computer model allows you to transform and supplement the subsequent calculations.

As a result of computer modeling of combustion processes in a system with convective heat recirculation, confirmed by some experiments, it was shown that

– in this system

1. a) it is possible to sustain combustion in a channel with a diameter less than critical,
2. b) combustion with velocities greater than the normal velocity of the free flame and gas temperature may exceed the adiabatic temperature of the free flame,
3. c) the flame is resistant to external influences caused by a change in the ambient temperature, changes in the gas flow rate and other factors.

The possibility of flame stabilization in a straight channel with a temperature gradient in the walls, which is created by the combustion products, is shown. These results allow us to conclude that this system is promising for creating, for example, micro-burners.

– A new type of instability has been discovered in the combustion of gas in micro-channels with a longitudinal temperature gradient in the walls of the channel. A feature of this type of flame instability is the presence of an inhomogeneous velocity profile of the gas in the channel and heat exchange with hot walls. The range of values of the gas flow rate at which this type of instability manifests itself is found. It is shown that in a radial channel this type of instability leads to the formation of rotating flame structures, in particular, a spiral flame detected in experiments.

5. Conclusion

The mathematical model of flame attenuation in narrow channels for different fire extinguishing and explosion suppression compositions is given. Such kind of flame distribution and attenuation could be considered for different media and channels but in given research it was considered for narrow channels. The effect on the combustion reaction is possible with gas mixture components concentration reducing, cooling the combustion zone and slowing down of chain reactions with the help of a phlegmatizing or inhibiting substances, of which the most universal and perspective are powder materials. As in the classical formulation, approximations are used about the constant density, heat capacity, and thermal conductivity of the gas. Caushy task for a second-order partial differential equation that describes the temperature distribution in a given region of space and its variation over time was solved. The numerical realization of heat transfer process was implemented in MatLab, and Adomian Decomposition Method was used for calculation of components of displacement of parts of fire extinguishing powders and burning reagents. The interface with input/output parameters was launched and tested. A package with name” TED in channels” (Thermoelastodynamics in channels) enables to reuse the names of classes and functions in different packages.

Conflict of Interest

The authors declare no conflict of interest.

Acknowledgment

Authors are grateful for scientific and methodological support to M. Auezov South-Kazakhstan State University, Kazakhstan.

1. Аlipova B.N., Alexeyeva L.A., Dadaeva A.N. Shock waves as generalized solutions of thermoelastodynamics equations. On the uniqueness of boundary value problems solutions // AIP Conference proceedings, 2017, V. 1798, I. 020003, pp. 1-8 DOI: 10.1063/1.4972595
2.  Fennandez-Pello A. C. Micro-power generation using combustion: issues and approaches. Twenty-ninth intern. symp. on combustion, Pittsburg, 2002, V. 40, no. 5, pp. 883– 899.
3.  Sitzki, L., Borer, K., Wussow, S. Schuster, E., Maruta, K., Ronney, P. and Cohen, A., “Combustion in Microscale Heat-Recirculating Burners”, 38th AIAA Space Sciences & Exhibit, Reno, NV, 2001, V. 22, no. 3, p. 1087.
4.  Vican, J. Gajdeczko, B.F., Dryer, F.L., Milius, D.L., Aksay, I.A. and Yetter, R.A.”Development of a Microreactor as a Thermal Source for MEMS Power Generation” Proceedings of the Twenty-Ninth International Symposium on Combustion, Sapporo, Japan, 2002, V. 40, no. 5, pp. 906-916.
5.  Lloyd S. A. and Weinberg F. J. A burner for mixtures of very low heat content NATURE, 1974, V. 251, pp. 47–49.
6.  Jones A. R., Lloyed S. A., and Weinberg F. J. Combustion in heat exchangers // Proc. Roy. Soc. Lond., 1978, V. A369, pp. 97–115.
7.  Buckmaster J. D. The effects of radiation on streched flames // Combust. Theory Modelling, 1997, no. 1 pp. 1–11.
8.  Zamaschikov V.V., Minaev S.S. Limits of flame propagation in a narrow channel during gas filtration // Physics of Combustion and Explosion, 2001, V. 37, no. 1, pp. 25–31.
9.  Zeldovich Ya. B. The theory of propagation of a quiet flame // Journal of Energy and Solids, 1941, V. 11, I. 1, pp. 159–168.
10.  Minaev S.S., Babkin V.S. Propagation of a flame in a channel of variable cross section during gas filtration // Physics of Combustion and Explosion, 2001, V. 37, no. 1, pp. 16–24.
11.  Sapargalieva B., Naukenova A., Alipova B., Javier Rodrigo Illari, Shapalov Sh. The analysis of heat and mass properties of the fire extinguishing powder in effectiveness criteria // News of the National Academy of Science of the Republic of Kazakhstan. Series of Geology and Technical sciences, 2018,. ISSN 2518-170X (Online), ISSN 2224-5278 (Print), V. 3, no. 4 (430), pp. 51-61.
12.  M. Raoofian Naeeni, M. Eskandari-Ghadi, A. A. Ardalan, S. Sture, and M. Rahimian, “Transient response of a thermoelastic half-space to mechanical and thermal buried sources,” ZAMM 95 (4), 354–376 (2015).
13.  H. Mahmoodi Kordkhieli, G. Ghodrati Amiri, and M. Hosseini, “Axisymmetric analysis of a thermoelastic isotropic half-space under buried sources in displacement and temperature potentials,” J. Thermal Stresses 40 (2), 237–254 (2017).

(Click Here)

(Click Here)