1. Introduction

This paper is an extension of work originally presented in a conference [1]. Scheduling is a constrained allocation of resources to objects in space and time, aimed at minimizing the total cost of a set of used resources [2]. This involves creating schedules by temporarily assigning activities to resources considering one or more objectives and some constraints. Project scheduling in [3] with emphasis on testing the dependencies of ordered activities using Pearson’s Correlation Coefficient (PCC) is not centered on temporal scheduling which is the focus of this paper. Basically, PCC is used in [3] to obtain weights for activities and then classify them as dependent or independent so as to avoid frequent usage of same resources multiple times thereby reducing expenses and project duration. Temporal reasoning is a suitable methodology to synchronize operations, make allocations for resources, determine sequences of operations, and evaluate average earliness or tardiness of a schedule. Time, which is modeled by quantitative values and constraints, is used to represent every schedule [4, 5]. Formalizing time scheduling process is a complex task that involves different reasoning strategies, structures and elements from multiple languages. Several attempts of formalizing time schedules using classical techniques exist in the literature (simulated annealing [6], genetic algorithm [7], Tabu search [8, 9], case-based reasoning [10], and graph coloring approach [11, 12, 13, 14]. However, these approaches lack formalization and are not simple to implement needed semantics during problem solving. Moreso, their solutions, though functional, may be error prone when considering new sets of constraints. Ontology-based approaches are emerging to resolving such complexities due to their ease in interoperability and reuse of data. The identified time complexities in [1] can be resolved in the allocation reasoner (AR) by implementing the represented formal notations that describe the embedded semantics in the given rules applicable for inference in the weighted ontology framework. In this work, the heuristics are formalized through ontology [15], by explicitly incorporating all constraints that will give valid answers to the competency questions in the AR and to enable their execution by ontology reasons.

The focus of this work is to construct the basic rules handling the constraints in the timetabling process with the corresponding formal representations of the interval-based logic [16, 17] using first-order logic. Furthermore, the semantic model of the temporal scheduler is further described following Guarino’s formal ontology model.

The rest of the paper is organized as follows. Section 2 reviews related works and the use of ontology in scheduling problems including publishing meetings and event, resource allocation and timetabling while section 3 presents a formalization of the complexity reduction rules using first order logic and Allen’s interval relations for optimal time scheduling process. Section 4 presents the semantic model of the formal time scheduling ontology with different components for obtaining optimality of time, with a mathematical description of the conceptual model. In section 5, unified modeling language (UML) diagrams are used for structural and behavioral description of the time scheduling ontology (TSONT) while section 6 concludes the paper.

2. Related works

Ontology is a model building tool for specifying the scope of an application domain as well as it entities with the attributes or desired system features. Formally, it represents knowledge as a hierarchy of concepts within a domain and uses shared vocabulary to denote the concepts’ types, properties, functionalities and interrelationships. Ontology has been used as a structural tool to organize information and represent knowledge about the world in many areas, such as Artificial Intelligence (AI), Semantic Webs, Information Architecture, System Engineering, Library Science and so on. The formalization of rules enables the complexities found in the production of timetable to be managed and optimized. Ontology is capable of uniquely combining inherent techniques such as semantic search, ontology matching and ontology mapping to reduce the timescale and cost complexity in data and resolve conflicts that always occur. A typical complexity reduction case between two departmental ontologies is shown using the Anchor-PROMPT mapping technique [18]. The representation of the complexity types using the probability weighted ontology (PWO) [19] and the evaluation of its gold standard criteria using analytic hierarchy process (AHP) model [1] provide users with the window to reschedule any time based on the level of identified complexity to attain optimality. The various users’ windows for rescheduling are formally represented in the following sections.

Anchor-PROMPT is a conventional ontology mapper that automatically finds semantically similar features (described by terms) between two ontologies, taking a set of pairs of related terms from the source ontologies as input. Commonalities in two different departmental ontologies are mapped together to expose the causes of conflict or clash and resolve them. Consider the mapping of two departmental ontologies shown in figure 1 with Computer Science department in Faculty of Science as an anchor department, owning a certain course, CSC211. This course, CSC 211, is also being offered by students of the departments of Mathematics, Statistics and Physics in the same faculty, Vocational Education in faculty of Education, and Geo-Informatics in faculty of Environmental Studies. Ontology mapping involves linking the interactions around the course in the anchor department with that of the departments it is providing services to. In case of any clash or conflict with other courses offered by the students of any cooperating departments, the Time Scheduler or Allocation Reasoner (AR) along with the interval-based reasoning formally represented in this paper will re-schedule either of the courses concerned to resolve the conflict.

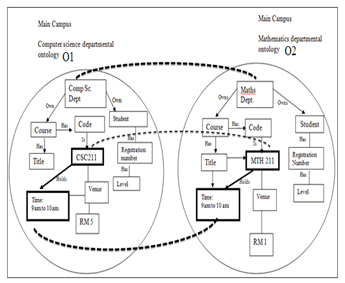Figure 1. Mapping of two departmental ontologies

As shown in Figure 1, the mapping of ontology O₁ and ontology O₂ by Anchor- PROMPT involves accepting pairs of related terms called anchors, defined by the user or automatically identified by lexical and syntactic matching, as input, from the source graph (ontology); and traversing the path between the anchors in the corresponding ontology. The link between the classes (nodes) defined by the hierarchical relations forms a path. The Anchor-PROMPT then compares the terms along these paths to find similar terms frequently appearing in similar positions on similar paths. In a nutshell, once the sets of similar terms are generated, e.g. {CSC211, MTH211}, scheduled for the same time{t_1, t₁}and in the same venue {v_1,v₁} which is also scheduled, the AR will be notified, and with the help of the interval-based reasoning, the AR will automatically reschedule either CSC211 or MTH211 for another time and venue respectfully giving priority to CSC211 on account that the high number of cooperating departments produces more complexities, as identified in PWO [1].The identified time complexities as resolved in the AR are expressively represented using formal notations to describe the embedded semantics in the given rules applicable for inference in the weighted ontology framework [1].

2.1 Ontology in scheduling and timetabling

Ontology has been applied in several scheduling task. The ontological framework in [20] specifies a meta-model that provides a vocabulary for formulating application model in a problem domain as well as a set of constraints on what can be expressed. The authors proposed the use of ontology to structure and simplify the process of constructing domain-specific problem-solving tools. Their work focused specifically on the task of scheduling, which ultimately led to the development of OZONE – a toolkit for configuring constraint-based scheduling systems.

With OZONE, it was possible to define domains, constraints as well as reusable and extensible concepts for describing and representing scheduling problem. In [21], a brief review of ontology for scheduling and publishing meetings and events was presented with a framework having a single consistent representation with a hierarchical structure capable of capturing some uncertainty and complexity that occur in real world system. The work attempts to present a balance between logical complexity in the ontology and the content language.

In [22], a generic task ontology for scheduling problems was proposed, expressing that ontology is generic if it is both domain and application independent. The work clearly described the class of scheduling tasks, independently of various ways by which these tasks can be solved. The given ontological framework provided a fairly fine-grained structure needed to build the scheduling system. The given cost related axioms ensure that an optimal solution or result is constructed by subsuming the various preferences in a scheduling task specification. Also, resource availability axiom was used to tackle the conflict between various jobs for the use of same resources depending on their overlapped time range.

An ontology-driven system for solving resources-constrained scheduling problems, orders-oriented and lean mass customization-based manufacturing was presented in [23]. This aimed at getting an easily customizable scheduling system that could be richly exploited by different manufacturers. Within the project Model Based Java Software Development Technology, it assumed the commencement of system development from the ontological conceptualization of the domain, constructing the models of the problem and implementing the system through transformation of models into codes.

In [24], a generic library problem solving method for scheduling application, following the limited coverage provided by different attempts made in the past in developing the libraries of scheduling problem-solvers was proposed. They subscribed to the Task-Method-Domain-Application knowledge modeling framework which provides a structured organization for the different components of the library and approached the work at two different levels – the task level and the method level. At the task level, a generic scheduling task ontology was constructed to formalize the space of scheduling problem. At the method level, a generic problem solving model of scheduling that generalize from the variety of approaches to scheduling problem-solving was constructed. In their work, they subscribed to a top down approach of scheduling construction and analyzed the importance of scheduling research both from the theoretical and engineering perspectives.

The authors in [25] proposed a framework which brought a step toward a generic semi-automatic timetabling tool. They investigated different types of timetabling problems and developed a framework for timetabling application with a central domain ontology tagged “ontology for timetabling”. The work developed a local search component that can deal with the search space based on problem characteristics passed on by the semantic components and was simplified into steps in order to generate good quality timetables in a reasonable amount of time. The first step was towards solving general problem that consists of mapping their data representation onto the ontology. The next step was using the tools to assists in determining the constraints and object of the problem. Custer et al. [25] based their timetabling ontology on the general OZONE scheduling ontology in [20] and developed a generic algorithmic component to generate a solution for real world problems.

The formal relationship between different components in a particular universe of discourse is described using formal languages. These descriptions are the basis for any ontology. An explicit description of the domain of discourse is formally represented in the formal ontology model in Figure 2 [26]. This model is adapted in this work for the semantic model of the formal time scheduling ontology in section 4, as it gives an explicit description of the domain of discourse.

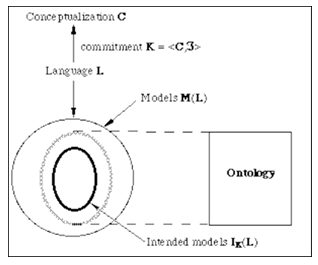Figure 2. Formal ontology model [26]

3. Complexity reduction rules and axiomatization

The set of competency questions – which are constraints to be satisfied, introduces the time complexities under consideration.  Some of the commonly applied competency questions include: Are students from other cooperating departments or faculty offering this course with students of the host department? Is the said course scheduled for the same time with course(s) in the serviced or cooperating department? Is the said course scheduled to hold in the same venue with course(s) in the other department? Are there students in other levels in the cooperating departments who enroll for this course? Is a particular lecturer scheduled to teach more than one course at the same time? Is the venue for the lecture on different campuses from that of students offering the course? Is more than one course allotted a particular venue at the same time? The Rule set comprises rules that address the constraints /complexities and also proposes axioms for their resolutions through the application of Allen’s interval relations. The assumption that a faculty has all  its constituent (departments) within the same locality (campus) hold for this work: A sub-set of the rules is given as follows:

R1:         IF student of dept₁ offers course₁ AND dept₁ NOT owns course₁ THEN time₁ for course₁ NOT overlaps time₂ for course₂ in dept₂.

R2:         IF course₁ holds at time₁ and course₂ holds at time₂ AND time₁ equals time₂ AND students offer course₁ and course₂ THEN time₁ and time₂ overlaps.

R3           IF course₁ holds at time₁ and course₂ holds at time₂ AND time1 is during time₂ AND students offer course₁ and course₂ THEN time₁ and time₂ overlaps.

R4:         IF course₁   holds at time₁ and course₂ holds at time₂ AND time₁ starts with time₂ AND students offer course₁ and course₂ THEN time₁ and time2 overlaps.

R5:         IF course₁ holds at time₁ and course₂ holds at time₂ AND time₁ finishes at time₂ AND students offer course₁ and course₂ THEN time₁ and time₂ overlaps.

R6:         IF course₁ and course₂ are of the same department, dept₁, THEN reschedule course₂ to a different time from course₁ (NOT overlaps).

R7:         IF course₁ and course₂ are in the same faculty but different departments (dept₁ and dept₂), THEN time₁ and Time₂ for course₁ and course₂ respectivelyshould NOT overlaps or course₁ NOT during course₂.

R8:         IF course₁ and course₂ are not in the same faculty, THEN time for course₁ and time for course₂NOT overlaps and NOT meets.

R9:         IF time₁ for course₁ and time₂ for course₂ meet, THEN time₂ for course₂ or time₁ for course₁ will be re-scheduled for next available time (NOT meets)

R10:       IF time for course₁ and course₂ are equal AND venue for course₁ is the same venue as venue for course₂, THEN course₂ should be re-scheduled for the next available time or course₂ re-scheduled for the next available venue

R11:       IF time for course₁ and course₂ are equal or meet, AND the lecturer teaching course₁ in campus₁ is also scheduled to teach course₂ in campus₂ within the space of a period, THEN course₂ should be res-scheduled for another time greater than a period.

R12:       IF course₁ is fixed to hold at time₁ at campus₁ AND course₂ time₂ at campus₂ THEN time₁ NOT meets time₂.

R13:       IF students who previously failed course₁ offer course₁ again, and are taking lectures at time₁ THEN time₂, for their current level course, NOT overlaps time₁.

R14:       IF course₁ in campus₁ and course₂ in campus₂, THEN time₁ for course₁ and time₂ for course₂ NOT meets or NOT overlaps.

R15:       IF venue capacity is less than students’ enrolment in course₁ THEN re-schedule course₁ another suitable venue.

Formalizing the complexity reduction rules in the previous section explicitly and expressively using First-Order Logic(FOL) yields the following AX1 to AX15 as axioms. The conventional approach of conceptualizing domain concepts; lecturer, student, venue and time with relations specific to the domain under consideration: owns, has, offers, holds and teaches, results in a non-optimal time scheduling. This therefore calls for the inclusion and utilization of the Allen’s interval relations; overlaps, meets, equals, during and their negations. Axioms AX1 to AX15 are rule instances that form the basis for the AR based on ontology and produces an optimal time-scheduling process.

Let S,V,T,C, L represent students, venue, time, course and levels respectively. Let S={s₁, s₂, … s_n} be the set of students,              V={v₁, v₂, … v_n} be the set of venues,  CS={cs₁, cs₂, … cs_n} be the set of courses, T={t₁, t₂, … t_n} be the set of time slots , P = {p1, p2, …, p3} be the set of campuses and L={L₁, L₂, … L_n} be the set of students level

AX1:       s, d1, cs1, t1,  cs2, d2, t2,

offers(s,cs1)owns(d1,cs1)offers(s,cs2) owns(d2,cs2)

cooperates(d1, Host, d2, Serviced).

AX2:       s, cs1, t1, cs2, t2.

holds(cs1,t1)holds(cs2,t2) equals(t1,t2)offers(s, cs1)  offers(s, cs2)

overlaps(t1, t2).

AX3:       s, cs1, t1, cs2, t2.

holds(cs1,t1)holds(cs2,t2)

during(t1,t2) offers(s, cs1)

 offers(s, cs2)overlaps(t1, t2).

AX4:       s, cs1, t1, cs2, t2.

holds(cs1,t1)holds(cs2,t2)

starts(t1,t2) offers(s, cs1)  offers(s, cs2)

overlaps(t1, t2).

AX5:       S, cs1, t1, cs2, t2.

holds(cs1,t1)holds(cs2,t2) finishes(t1,t2)offers(s, cs1)  offers(s, cs2)overlaps(t1, t2).

AX6:       cs1, t1, d1, cs2, t2.

owns(d1,cs1)owns(d1,cs2) holds(cs1,t1)holds(cs2,t2)equals(t1,t2) equals(l1, l2)overlaps(t1, t2).

AX7:       cs1, t1, d1, fac1, cs2,t2, d2. fac2.

owns(d1,fac1,cs1)owns(d2, fac2, cs2)

overlaps(t1,t2) during(holds(cs1, cs2)) .

AX8:       cs1, t1, cs2, t2,  t.

holds(cs1,t1)holds(cs2,t2)  finishes(t1,t) starts(t2,t)  meets(t1, t2).

AX9:       cs1, t1, d1, fac1, cs2, t2, d2. fac2.

owns(d1, fac1, cs1)   owns(d2, fac2, cs2)  equals(f1,f2)

meets(t1,t2)  overlaps(t1, t2).

AX10:     cs1, t1, v1, cs2, t2, v2.

holds(cs1,t1)holds(cs2, t2) equals (v1, v2)

equals(t1, t2).

AX11:     cs1, t1, p1, cs2, t2, p2.

holds(cs1,t1, p1)  holds(cs2, t2, p1) equals (t1, t2)  equals(p1,p2) teaches(lect,p2) teaches (lect, p2)

overlaps (t1, t2)meets (t1, t2)

AX12:     cs1, t1, p1, cs2, t2, p2.

holds(cs1,t1,p1) holds(cs2, t2, p2) equals (t1, t2) equals (p1, p2)  meets (t1, t2)

 AX13:     s, cs1, t1, d1, cs2, t2.

offers(s,cs1,t1) offers(s, cs2, t2) owns(d1, c1)  equals(t1, t2)  equals(l1, l2) overlaps(t1, t2).

 AX14:     s, cs1, t1, d1, cs2, t2.

offers(s,cs1,cs2)

 holds(cs1, p1) holds(cs2, p2)

meets(t1,t2)overlaps(t1, t2).

 AX15:     s, cs1,v1, t1, nos,  v2, vcap.

offers(s, cs1, v1)  holds(cs1, v1, t1)  (nos>vcap) holds(cs1, v2)

 As an interpretation, axiom AX6 can be read thus: ‘For all students, courses and departments, there exist course cs2, such that cs2 is offered by student and department owns student and cs2 is not own by department. It therefore follows that time₁ for cs1 should not overlap with time₂ for cs2”.

This formalism utilizes offers and owns as domain-specific relations. It also explored a reverse relation to owns between students and departments.  The power of Allen’s interval relation, overlaps, is also brought into consideration not forsaking the expressive tools in FOL. The use of the universal and the existential qualifiers gave life to the axiom. Putting all these together in Protégé ontology tool where the departmental timetable ontology has been developed and mapped together with reasoning to make the task of responding to the earlier proposed competency questions an easy one. A general and optimal lecture timetable with clear semantics as described in the formal representation is thus achieved.

4. Semantic modeling of the formal time scheduling ontology

Figure 3 represents the semantic model of the formal time scheduling ontology with different components which are related accordingly to show how an optimality of time can be obtained. The semantic model of the formal time scheduling ontology is adapted from the semantic model by Guarino [26], where, Time Scheduling Ontology (TSONT) is defined as the conceptualization of the domain concepts expressed mathematically in equation (1). Further description of the conceptual model is explicated in equations (2) to (4), where a set of conceptual relations, R is on a structure, S being the model of the language L with vocabulary V.

C_TS  =< D_T , T_C , R >           (1)

<D_T , T_C> = DSR + AIR    (2)

The resulting model is given as < S, I > where,

 S = <D_T , R >                     (3)

and the usual interpretation function, I is expressed as I = V →   D_T R. Fixing the intentional Time Schedule by means of a structure such as < C_TS, P> where,

C_TS = < D_T, T_C, R> and P:V →  D_T R is an intentional interpretation, hence, K = < C_TS, P > is an Ontological commitment for L. That is, L commits to C_TS by means of K and C_TS is the underlying conceptualization of K. With the commitment,

                C_TS  =< D_T, T_C,  R, I >       (4)

where, C_TS is the time scheduling conceptualization, D_T is the timetabling domain, T_C is the interdepartmental allocation complexities, R is the relations, DSR is the Domain Specific Relation, AIR is the Allen Interval Relations_, I is the Interpretation, P is the Intentional Interpretation, S is the Structure, and K is the Ontological Commitment. The mathematical model in equation (1) is used to give a semantic interpretation that will further explicate the logic behind ontology.

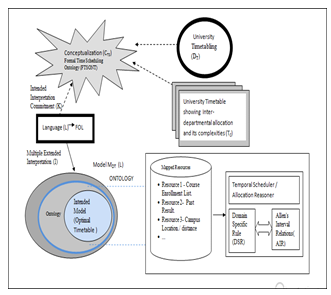Figure 3. Semantic model of the formal time scheduling Ontology

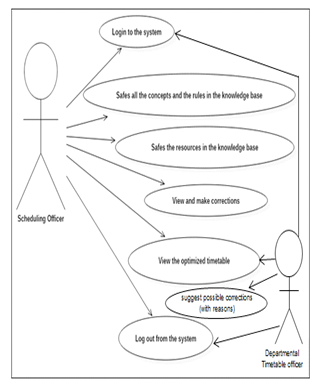Figure 4. Use case diagram for the TSONT framework

5. System design for TSONT model

5.1 Use case description

The Use Case diagram in figure 4 gives a clear understanding of the developed time scheduling ontology (TSONT) system. The concepts and the resources of the timetable are saved into the knowledge base by the scheduling officer, after a successful log in. The scheduling officer then sends the resources to the allocation reasoner or time scheduler for proper allocation of time. Furthermore, the officer can view the system outcomes, make corrections where necessary, and then review for optimized timetable, and then logs out. The departmental timetable officers can in turn log in to view the optimized timetable, suggest possible corrections for consideration and effect by the scheduling officer, and logs out.

5.2 Class diagram for TSONT framework

Figure 5 represents the class diagram of the TSONT framework, which shows the interactions between classes that constitute the domain of discourse. The student offers courses and the courses are taught by the lecturers. Courses are held in venues, and each venue has an interval of time assigned for it. The venue also has its capacity which informs the number of students that can be allocated to the venue.

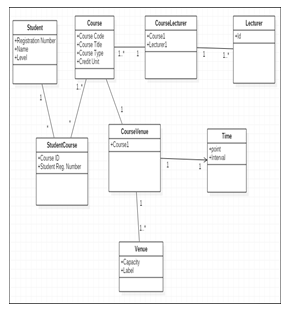Figure 5.  Class diagram for TSONT framework

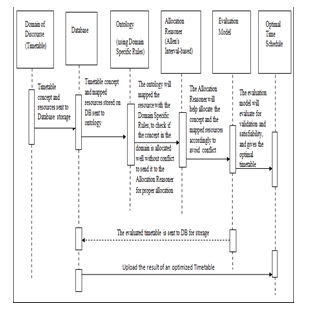Figure 6. Sequence diagram for the TSONT framework

5.3 Sequence diagram

Figure 6 represents the sequence diagram of how the proposed TSONT system works. The resources used for time schedule and the concepts of the domain of discourse are sent to the database (DB) for storage. The ontology picks the concepts and resources needed for time schedule and sends them to the AR, which helps the rule-based and the interval-based relations, check and allocate the courses, lecturers, venue to the time-slots and to a particular set of students, considering the students who failed or dropped course at a lower level.

The AR sends the results to be evaluated by an ontology evaluation tool, for validation and satisfiability, after which the conclusion of a time complexity free time schedule is sent back to the DB for storage and future reuse. The DB uploads the optimized time schedule for printing and distribution.

6. Conclusion

The university timetabling, an instance of space-time related conflicts or complexities, requires the design of an interval-based temporal ontology to help in its resolution demands full understanding of how the ontology handles the constraints that will answer the stated competency questions. The formal axioms from the stated rules update the constraints in the ontology using the interval based relations. The implementation of the represented formal notations to describe the embedded semantics in the given rules is applicable for inference in the weighted ontology framework. It aims at formalizing the heuristics through ontology, by explicitly incorporating all constraints that will give valid answers to the competency questions in the AR and enabling their analysis and resolution by the ontology-based reasoners. The formal semantic model further explicates the ontology and shows how it is applicable for intelligent complexity reduction and resolution in time scheduling process. The time scheduling ontology based on this formal semantic model will provide an optimal time table schedule.

Conflict of Interest:

The authors declare no conflict of interest

1.  P. U. Usip, U. G. Inyang, D. E. Asuquo, E. M. Umoren, “An evaluation model for a probability weighted ontology of temporal complexities”, in Proceedings of 2nd IEEE International Conference on Computational Systems and Information Technology for Sustainable Solutions (CONTISS 2017), Bengaluru, India, 159-165, 2017.
2.  A. Wren, “Scheduling, timetabling and rostering – A special relationship”? International Conference on the Practice and Theory of Automated Timetabling (PATAT 1995), 46-75, 1995.
3.  J. Shafi, A. Waheed and S. Sanober (2016). Dependency Test: Portraying Pearson’s Correlation Coefficient Targeting Activities in Project Scheduling. International Journal of Advanced Computer Science and Applications. 7(9). 351-356. 10.14569/IJACSA.2016.070948.
4. A. Modupe, O. Olusayo, and O. Olantunde, “Development of a University lecture timetable using modified genetic algorithm approach”, International Journal of Advanced Research in Computer Science and Software Engineering, (4), 163-168, 2014.
5.  S. Kristiansen and T. R. Stidsen, “A comprehensive study of educational timetabling: A survey”, Department of Management Engineering, Technical University of Denmark, DTU Management Engineering Report, (8), 2013.
6.  D. Abramson, “Constructing school timetable using simulated annealing: sequential and parallel algorithm”, Management Science, 37(1), 98-113, 1994.
7.  A. Colorni, M. Dorigo, and V. Manniezzo, “A genetic algorithm to solve the timetable problem”, Journal of Computational Optimization and Applications, 1, 90-92, 1992.
8. N. Ibaraki, “Tabu Search for the constraint satisfaction problem as a general problem solver”, European Journal of Operational Research, 599-623, 1998.
9.  E. K. Burke and J. Newall, “Enhancing timetable solutions with local search methods”, In: Burke, E. K., DeCausmaecker, P. (eds.): Selected papers from the 4th International conference on the Practice and Theory of Automated Timetabling. Lecture Notes in Computer Science, Vol. 2740, Springer-Verlag, Berlin Heidelberg New York, 344- 354, 2003.
10.  Q. Rong, “Case-base reasoning for course timetabling problem”, PhD Thesis, University of Nottingham, 2002.
11.  J. P. Rickman, “The design of a course-timetabling system using graph-coloring and artificial intelligence”, Honors Program Theses, Paper 15, 2014. https://scholarship.rollins.edu/cgi/viewcontent.cgi?article=1014 HYPERLINK “https://scholarship.rollins.edu/cgi/viewcontent.cgi?article=1014&context=honors”& HYPERLINK “https://scholarship.rollins.edu/cgi/viewcontent.cgi?article=1014&context=honors”context=honors
12.  R. Ganguli and S. Roy, “A study on course timetable scheduling using graph coloring approach”, International Journal of Computational and Applied Mathematics, 12(2), 469-485, 2017.
13.  R. K. Bania and P. Duarah, “Exam time table scheduling using graph coloring approach”, International Journal of Computer Sciences and Engineering, 6(5), 84-93, 2018.
14.  R. P. Badoni, and D. K. Gupta, “A graph edge colouring approach for school timetabling problems”, International Journal of Mathematics in Operational Research, 6(1), 117–132, 2014.
15.  J. Roa, E. Reynares, C. M. Laura and P. D. Villarreal, “Ontology-based heuristics for process behavior: formalizing false positive scenarios”, 2017. Available from: https://www.researchgate.net/publication/316743617 [accessed Jan 13 2019].
16.  J. Allen, “Maintaining knowledge about temporal intervals”, Communications of the ACM. 26(11), 832-843, 1983.
17.  M. Hemalatha, V. Uma and G. Aghila, “Time ontology with reference event based temporal relations”, International Journal of Web and Semantic Technology, 3(1), 23-31, 2012.
18.  N. Noy and M. Musen, “Anchor-PROMPT: using non local context for semantic matching”, in Proceedings of the Workshop on Ontologies and Information Sharing at the International Joint Conference on Artificial Intelligence (IJCAI), Seattle, Washington, 2001.
19.  A. Formica, M. Missikoff, E. Pourabbas and F. Taglino, “Bayesian approach for weighted ontologies and semantic search”, in Proceedings of the 8th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (2), 171-178, 2016.
20.  S. Smith and A. Becker, “An ontology for constructing scheduling system”, AAAI, Spring, 120 Symposium on Ontology Engineering, Newport Beach, California, 129, 1997.
21.  C. Sayers and R. Letsinger, “An ontology for publishing and scheduling events and the lessons learned in developing it”, in Workshop on Ontologies in Agent Systems, 1st International Joint Conference on Autonomous Agents and Multi-Agent Systems (AAMAS 2002), Bologna, Italy, 2002.
22.  D. Rajpathak, E. Motta and R. Roy, “A generic task ontology for scheduling applications”, in Proceedings of the International Conference on Artificial Intelligence, Las Vegas, 2001.
23.  J. Sanko and V. Kotkas, “Ontology-driven scheduling system for manufacturing”, Baltic Journal of Modern Computing, 4(3), 508 – 522, 2016.
24.  D. G. Rajpathak, E. Motta, Z. Zdrahal and R. Roy, “A generic library of problem solving methods for scheduling applications”, IEEE Transactions on Knowledge and Data Engineering, 18(6), 815-828, 2006.
25.  N. Custers, P. De Causmaecker, P. Demeester, and G. Berghe, “Semantic component for timetabling”, International Conference on the Practice and Theory of Automated Timetabling (PATAT 2004), 17-33, 2004.
26.  N. Guarino, (Ed.), “Formal ontology”, in Proceedings of the First International Conference on information systems (FOIS’98), 46, 3-15, Trento, Italy, 1998.

(Click Here)

(Click Here)