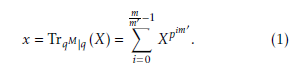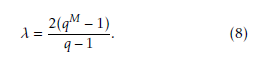1. Introduction

In this IoT era, we communicate with each other through the internet. Therefore, secure communica- tion is the major matter of concern. We use symmetric cryptosystems (Advanced Encryption Standard (AES) [1]) and asymmetric cryptosystems (Rivest Shamir Adleman (RSA) [2], and Elliptic Curve Cryptography (ECC) [3]) to establish a secure communication. A pseudo-random number is one of the crucial parts of these cryptosystems. More specifically, in case of cryptography, to generate the keys (public key, pri- vate, session key, and so on) a pseudo-random number generator is used. A prominent pseudo-random num- ber generator is essential to generate pseudo-random number having randomness property (along with other good statistical properties). Consequently, the security of these cryptosystems deliberately depends upon the randomness property regarding a sequence. Thus, it is mandatory to evaluate the randomness of a sequence before utilized them in any cryptosystems. Basically, two crucial properties namely the linear complexity

[4] and the distribution of bit patterns regarding a sequence are nowadays well-known to check the ran- domness of a pseudo-random sequence. In this work, the authors restrict the discussion on the distribution of bit patterns property to evaluate the randomness of a sequence.

Most renowned pseudo-random number generators are the Mersenne Twister (MT) [5], Blum-Blum-Shub (BBS) [6], Legendre sequence [7, 8], and M-sequence [9]. Among those the former two pseudo-random num- ber generators (MT and BBS) are well-known consider- ing their applications in cryptography rather than the theoretical aspect. On the other hand, the M-sequence and Legendre sequence are prominent geometric se- quences regarding the theoretical aspect. As a result, the authors attracted in the pseudo-random sequence generation research area by observing the theoretical prospect on the M-sequence and Legendre sequences.

The Legendre sequence [7, 8] is generated by ap- plying the Legendre symbol over the odd characteris- tic field. It has a long period, high linear complexity, and the distribution of bit patterns of the Legendre sequence is known to be close to uniform [10, 11]. On the other hand, M-sequence is generated by a linear recur- rence relation over the finite field. It has a maximum period but minimum linear complexity. In addition, M- sequence [9] is well-known for its uniform distribution of bit patterns [12]. Our previous work on geometric sequence [13] combines the features of the Legendre sequence and M-sequence. As mentioned previously, linear complexity and distribution of bit patterns are the important measures to evaluate the randomness of a sequence. So, regarding the linear complexity, our previous sequence [13] always possess high value. Unlike the linear complexity, the distribution of bit patterns in [13] doesn’t reaches up to the mark alike the Legendre sequence and M-sequence. Hence, its a scope to improve the distribution of bit patterns in our previous sequence.

The trace calculation is an important step during our sequence generation procedure. Lets focus on the important aspect regarding this calculation. In case of prime field F_p, the trace function maps an element of the extension field F_qM to an element of the prime field F_p. Therefore, the number of possible trace outputs will be in the range of  0    p    1 .  In other words, if we calculate the trace over the prime field, then it will output p kinds of values.  On the other hand, in case of the sub extension field F_q, the trace function maps an element of the extension field F_qM to an element of the sub extension field F_q and the number of possible trace outputs will be in the range of 0 q 1 which means the trace outputs q kinds of values. It should be noted that here M = m/m^j, q = p^mj , and m^j be one of the factors of m. From the theoretical perspective, more variation in the trace values contribute to the better appearance of bits (0 and 1) in a sequence. This is one of the important aspects to consider the sub ex- tension during the sequence generation procedure to improve the distribution of bit patterns in our previous sequence [13]. After utilizing the sub extension field, the detailed improvement in distribution of bit pat- terns is introduced in the result and discussion section in this paper.

Recently, the authors started to consider the sub extension field during the sequence generation proce- dure, which is a new dimension of our research work on generation of pseudo-random sequence (whereas our previous works on binary sequence [13] and multi- value sequence [14, 15] are considered in the prime field). As a result, our recent works on binary sequence

[16] and multi-value sequence [17] experimentally ob- served the linear complexity, autocorrelation proper- ties, respectively. As mentioned previously, the dis- tribution of bit patterns is an important measure to evaluate the randomness of a sequence. Thus, the authors of this paper consider the distribution of bit patterns in a binary sequence which generated over the sub extension field.

The Legendre sequence and M-sequence are the base of the sequence research area. Their properties are already proven, therefore many researchers attracted by those sequences. As mentioned previously, our se-

quence also generated by the idea of the Legendre and M-sequences. Consequently, the authors thought that its properties can be theoretically proven and fortu- nately its proven (which shown in the later section of this paper). This is one of the contributions of the authors in this paper. Moreover, they also make a comparison between the binary sequence defined over the sub extension field with their previous work on binary sequence in terms of distribution of bit patterns property. According to the comparison result, binary sequence (defined over sub extension field) holds much better (close to uniform) distribution of bit patterns than the previous binary sequence [13]. Finding this improvement by considering the sub extension field is the major contribution of this paper.

The authors of this paper observed the distribution of bit patterns in a binary sequence which generated by a primitive polynomial, trace function, and Legen- dre symbol over the sub extension field. In brief, the sequence generation procedure is as follows: at first, it uses a primitive polynomial over the odd characteristic field F_p to generate maximum length vector sequence as elements in F_qM , then the trace function maps the extension field F_qM elements to the sub extension field F_q elements, and finally the Legendre symbol bina- rizes the sub extension field F_q elements to a binary sequence. The authors already observed the period, autocorrelation, cross-correlation, and linear complex- ity properties of the binary sequence (which generated over the sub extension field) in their previous works [16, 17]. Thus, this paper focused on the distribution of bit patterns property. In brief, the authors count the number of appearances for each n-bit patterns (where

• n  (m/m^j)). After observing many experimental

results, the authors found that the number of appear-

ances of each bit pattern is related to the number of zeros contained in each bit pattern. Furthermore, the authors theoretically proven the distribution of bit pat- terns equation. Moreover, they also make a comparison with their previous work [13].

Throughout this paper, p and q denote an odd prime number and its power q = p^mj , respectively, where m be a positive integer which mainly denotes

extension degree and m^j be one of the factors of m. In addition, M = m/m^j and Fq∗ denotes the multiplicative group of F_q, that is Fq∗ = F_q − {0}.

2. Preliminaries

This section briefly explains some fundamental con- cepts of the finite field theory such as group, field, primitive polynomial, trace function, Legendre symbol, and dual bases. Then, binary sequence is introduced along with its period and distribution of bit patterns properties.

2.1. Group

A group is a non-empty set G with a binary operation

• on its elements denoted as < G, ◦ >, which satisfiesthe following axioms.

• Closure For _a,b G, the result of a  b also exists in G and it is uniquely

• Associativity Elements in group G should fol- low associativity. i.e. (a ◦ b) ◦ c = a ◦ (b ◦ c), where a, b, c ∈ G.
• Identity element There exists an element e ∈ G such that ∀_a ∈ G, a ◦ e = e ◦ a = a.

• Inverse element For _a G, there exists an ele- ment b G such that a b = e = b a, where b is called inverse element of a.

Commutative group A group G will be commutative if a b = b a for all a, b G.

Group generator For a given group G if there is an element g G such that for any a G there exists an unique integer i with a = gⁱ then g will be called as a generator of G.

Order of a group The order of a group G often denoted as #G is the number of elements in the group G. Cyclic group A group G will be cyclic if there exists at least one generator g        G and it is denoted as G =< g >. From the definition of cyclic group, it can be visualized that each element in a cyclic group can be generated with iterative operations of generator g which shown in the following Figure 1.

Figure 1: cyclic group.

Multiplicative group A cyclic group is called multi- plicative if we tend to write its group operation in the same same way we do multiplication, that is

f = g · x or f = g^x.

2.2.  field

A field < F , +, · > is a set that obeys two binary opera- tions denoted by + and · , such that

• F is a commutative group with respect to addi- tion (+) having identity element
• Let F^∗ is a subset of F having non-zero elements of F e. F^∗ = F − {0}. Then F^∗ will be called a

commutative group with respect to multiplica- tion ( ), where every element should have multi- plicative inverse in F^∗.

• For all a, b, c ∈ F the distributive law will be fol- lowed, e. a·(b+c) = a·b+a·c and (b+c)·a = b·a+c·a.

Sub field Let F₁ is a sub field of a field F.  Then F₁ will be called a sub field if F₁ obeys the laws of field with respect to the field operation inherited from F. In addition, if F₁ s F, then F₁ is a proper sub field of F.

Prime field Let p be a prime. The ring of integers mod- ulo p is a finite field of characteristic p having field order p denoted as F_p is called a prime field.

Extension field A subset F₀ of a field F that is itself a field under the operations of F will be called a sub field of F.  In this case, F is called an extension field of F₀. An extension field of a prime field F_p can be represented as m-dimensional vector space that has m elements in F_p. Let the vector space be the m-th exten- sion field be denoted as F_qM . The order of a extension field F_qM is given as p^m (here q = p^mj and M = m/m^j).

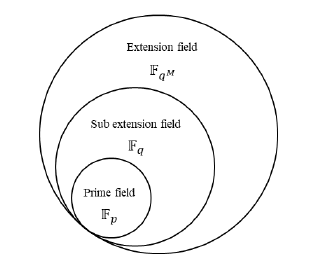
In very brief, it can be said that a prime field (F_p) is a subset of sub extension field (F_q) and sub extension field F_q is also a sub set of extension field F_qM which shown in Figure 2.

Figure 2: Fp ⊂ Fq ⊂ FqM .

2.3. Primitive Polynomial

Consider a polynomial f (x) of degree m over prime field F_p. If it is not factorized into smaller degree polynomials over the prime field F_p, it is called an ir- reducible polynomial. Consider the smallest number e such that x^e − 1 is divisible by f (x) over F_p, it is known that e becomes a factor of q^M 1. Then f (x) is espe- cially called a primitive polynomial, when e is equal to q^M 1. Its zero ω belongs to the extension field F_qM

and it becomes a primitive element in F_qM that gener- ates every non-zero element in F_qM   as its power ωⁱ (for i = 0, 1, 2, . . . , q^M−2).

2.4. Trace function

This work utilizes the trace function to map an element of the extension field X ∈ F_qM to an element of the sub extension field x ∈ F_q as, m −1

2.7. Binary Sequence and Its Properties

This paper introduces a binary sequence along with its period and distribution of bit patterns properties as follows.

• Generation Procedure and Period

A crucial point, the above trace becomes an arbitrary element in F_q and the trace function has a linearity property over the sub extension field F_q as follows,

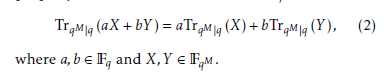Let ω be a primitive element in the extension field F_qM , where M = m/m^j, m be a composite number which de- notes the extension degree of the primitive polynomial, and m^j be one of the factors of m. Then, by utilizing the trace function and Legendre symbol a binary sequence S is generated as follows:

2.5. Legendre Symbol

The  Legendre  symbol  a/q 2   is  used  to  check  the

quadratic residue for any arbitrary element a in F_q. It is defined as,

where  i  =  (0, 1, 2, . . . , λ − 1, . . .),  s_i  ∈ 0, 1  and  f₂(·)  be  a mapping function, which translates the 0, 1, and p − 1

values sequence generated by the Legendre symbol

to a pseudo-random binary sequence. This mapping function is defined as follows:

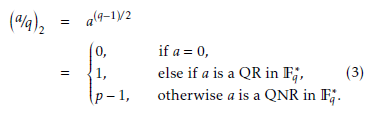
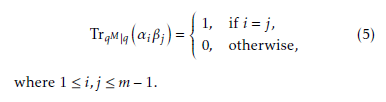
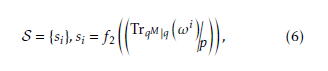
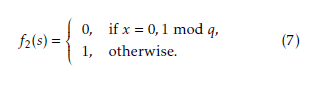Here, QR and QNR stand for Quadratic Residue (QR)

and Quadratic Non-Residue (QNR), respectively. Ad- ditionally, the non-zero element a is called the QR if it has a square root in F_q, otherwise a is called the QNR. In this paper, the Legendre symbol is used for translat- ing a vector sequence generated by the trace function over F_q to a binary sequence. Above mentioned QR and QNR in F_q holds the following important property. Non-zero elements are the roots of x^q−1   1 in Fq∗

over F_q without any duplicates. Since it is factorized

as follows:

After observing many experimental results, the au- thors derive the equation for the period λ of the binary sequence as,

• Distribution of Bit Patterns

From the viewpoint of security, the distribution of bit patterns is as important as the linear complexity. If

It is thus found that the number of QR’s and QNR’s in Fq∗ are the same and it is given by (q    1)/2. In addi- tion, these numbers are important part in proving the

theorem in the later section of this paper.

2.6. Dual Bases

The dual bases plays an important role in proving the theorem shown in this paper. It is defined as follows:

Let F_qM be a finite field and F_q be a finite extension of F_qM . Then the two bases              =  α₀, α₁, . . . , α_m−1   and

= β₀, β₁, . . . , β_{m 1}  of F_q over F_qM   are said to be the

dual (or complementary) bases if a sequence holds the uniform distribution of bit pat- terns, then it becomes difficult to guess the next bit after observing the previous bit patterns. For example, let’s assume a binary sequence having a period of 12 as ₁₂ = 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0 . If we observe the 1-bit pattern in this sequence, then we can find that it has a uniform distribution of 1 and 0. In other words, 1 and 0 appear same in number. However, when we check 2-bit patterns on   ₁₂, we find that it only has two types of patterns (10 and 01). In this case, we can easily pre- dict the next bit patterns after observing the previous patterns. For example, let us make a sub-sequence of ₁₂ as 1, 0, 1, 0, x₅, x₆ , we can easily guess x₅ and x₆ as x₅ = 1 and x₆ = 0. Therefore, it is also essential to eval-

TrqM |quate the distribution of bit patterns of the sequence to confirm its randomness. In other words, the unifor- mity of the distribution contributes to the randomness

where 1 ≤ i, j ≤ m − 1.

from the viewpoint of unpredictability.

3. Distribution of Bit Patterns in Binary Sequence

In this section, we will introduce the bit  distribu- tion of binary sequence which generated over the sub extension field. In addition, bit distribution of M- sequence and Legendre sequence is also introduced here. Throughout this section b⁽ⁿ⁾, Z(b⁽ⁿ⁾) and D_S (b⁽ⁿ⁾)

denotes a bit pattern of length n, number of 0’s in b⁽ⁿ⁾,

uniform. Let, p = 23, then the Legendre sequence of period 23 becomes as follows.

S23 = {0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 1}. (10)

The distribution of n-bit pattern in (10) is shown in Table 2. In case of Legendre symbol, bit patterns ap- pearance is close to uniform.

Table 2: Bit distribution of the Legendre sequence S  .and number of appearance of b⁽ⁿ⁾ in S_λ

For example, in a binary sequence of period 15, a 3-bit pattern b = 101 appears 4 times. Then, these notations become b⁽³⁾ = 101, Z(b⁽³⁾) = 1, and D_S15 (b⁽³⁾) = 4.

3.1         Bit Distribution of M-sequence

The M-sequence [9] is generated by a linear recurrence relation over the finite field. M-sequence has a maxi- mum period and uniform distribution of bit pattern except for the case of Z(b⁽ⁿ⁾) = n but it has minimum linear complexity. Let, f (x) = x⁴ + x + 1 be a primitive polynomial over F₂, then using the linear recurrence relation a M-sequence of period 15 becomes as follows.

The distribution of n-bit pattern in (9) is shown in Table 1, here 1 n m. In the case of M-sequence, ex- cept the all-zero pattern, every pattern appears same in number. For example, when n = 3 all patterns ap- pear 2 times (except 000 pattern). In other words, they are uniformly distributed. Every M-sequence has such good distribution of bit pattern feature.

Table 1: Bit distribution of the M-sequence S15.

n	b(n)	Z(b(n))	DS23 (b(n))
1	0	1	12
	1	0	11
2	00	2	6
	01	1	6
	10	1	5
	11	0	5
3	000	3	3
	001	2	3
	010	2	3
	100	2	3
	011	1	2
	101	1	3
	110	1	2
	111	0	2

3.3         Bit Distribution of the Proposed Bi- nary Sequence

Let S_λ be a(binary sequence of having a period of λ. Again, let b ⁿ⁾, Z(b⁽ⁿ⁾), and D_S (b⁽ⁿ⁾) denotes a bit pat-

tern of length n, number of 0’s in b⁽ⁿ⁾, and number of appearance of b⁽ⁿ⁾ in _λ, respectively. Then, the dis- tribution of bit patterns in the binary sequence which defined over the sub extension field can be given by the following theorem.

n b(n) Z(b(n)) DS15 (b(n)) 1 0 1 7 1 0 8   2 00 2 3 01 1 4 10 1 4 11 0 4       3 000 3 1 001 2 2 010 2 2 100 2 2 011 1 2 101 1 2 110 1 2 111 0 2

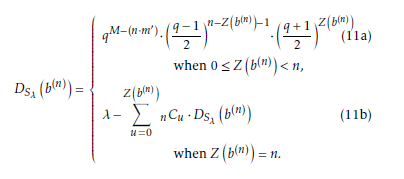3.2. Bit Distribution of LegendreSequence

Legendre sequence [7, 8] is generated by applying the

Let ω be a primitive element in the extension field F_qM , where M = m/m^j, m be a composite number which denotes the extension degree of the primitive polyno- mial, and m^j be one of the factors of m. Then, utilizing the trace function and Legendre symbol one period of a binary sequence is generated as follows.

Legendre symbol over the odd characteristic field. Leg- endre sequence has a long period, high linear com- plexity, and the distribution of bit pattern is close to

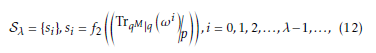Here λ be the period of the sequence and it is given by

of these coefficients as

a_i,0, a_i,1, . . . , a_i,(n−1) . Addition-

the following equation as,

ally, all the above trace values belong to the sub exten-

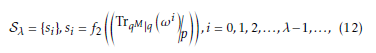
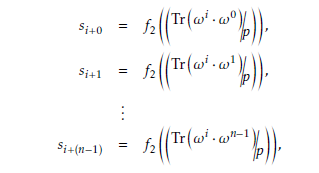sion field F_q. Furthermore, ωⁱ 0 ≤ i ≤ q^M − 2 in (15) represents every non-zero vectors in the extension field F_qM as,

At first, a primitive polynomial is used, then the trace value is calculated, then the Legendre symbol outputs zero, QR or QNR in F_q, and finally the sequence coeffi-

According to the trace property, non-zero F elements cients s_i is given by the mapping function f₂( ).

The authors of this paper observe the distribute appear q^M−mj

times and zero appears one less than

tion of n-bit patterns in a binary sequence. It should be noted that here n satisfies 1     n     (m/m^j) rela- tion. The  distribution  of  n-bit  patterns  evaluated by observing the consecutive sequence coefficients (s_i, s_i+1, . . . , s_i+(n−1)). Particularly,

the other elements i.e.  q^M−mj     1 times in the above equation.

• Relation Between the Sequence Coefficients With the Trace Values and Legendre Symbol

Depending on the three different types of trace values (0, QR, and QNR), the Legendre symbol outputs three different values (0, 1, and p 1), and finally the map- ping function outputs 0 and 1 as sequence coefficients s_i . This dependency between the trace and Legendre

symbol is explained as follows.

Table 3: Relation between the sequence coefficients with trace and Legendre symbol calculation -I.

where 0  i   (q^M   2).  By observing the above se- quence coefficients, the distribution of bit patterns D λ is determined by the following trace values.

Let       = α₀, α₁, . . . , α_{m 1} be a basis, ω be a primitive element and with this basis ωⁱ is represented as, m,−1

According to the above table, the sequence coefficient 0 comes from the two cases: one is for the Tr(0) case and another one is for the QR in Fq∗ case. To deal

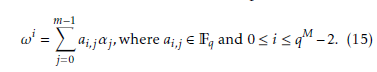Again let B = {ω⁰, ω¹, . . . , ωⁿ⁻¹, β_n, . . . , β_m−1} be a dual basis of A in F_q over F_qM . Then we also have with this two cases uniquely, let us denote 0 and 0 for the first and second cases, respectively. In addition, 1 comes for QNR in Fq∗ case.  Thus the above table can be further modified as follows.

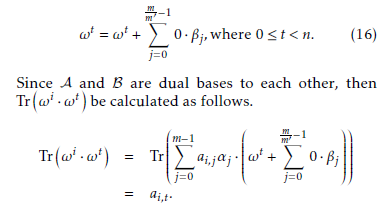Table 4: Relation between the sequence coefficients with trace and Legendre symbol calculation -II.

si   Tr ωi 0 0 0 QR in Fq∗ 1 QNR in Fq∗

Therefore, by usi ng t he dual basis, the distribution of To distinguish the appearance of 0, this paper uses bit patterns D_Sλb(n) determined by the trace values the notation 0, when zero comes from Tr(0) and 0 when becomes as follows. zero comes from QR. Let the number of 0 be denoted by u and T_u,n denotes the number of bit patterns in

In the following section, the distribution of bit patterns in the binary sequence defined over the sub extension

Accor ding  to the above equation, T_n can be calculated by Z b⁽ⁿ⁾ . In addition, there are _nCZ(b(n)) possible bit field theoretically proven. patterns that have the same Z b

To calculate the

• Proof of (11a)

DSqM −1

 b⁽ⁿ⁾  for each b⁽ⁿ⁾, T

needs to be divided by

The period of the binary sequence is given by the fol- lowing equation as,

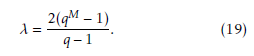
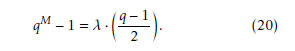
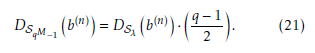
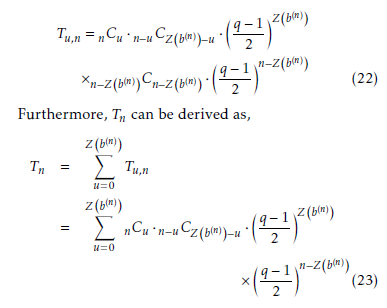
As mentioned previously, when the trace value is equal to 0 or QR, then the sequence coefficients be- comes 0 and 0, respectively. In addition, if the trace value is equal to QNR, then the sequence coefficients beco mes 1. Additiona lly, u denotes the number of 0 in

Thus, (24) becomes as follows:

From the (21), D_Sλ  b as follows, holds the following relation

Therefore, using the (27), D_Sλ    (n)   can be given by the end mj = 2. following relation as,

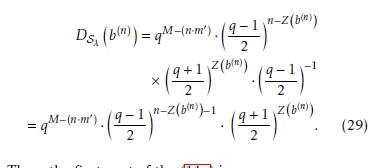Table 5: Bit distribution of the binary sequence   52 with p = 5, m = 4,

n Hwt(b(n)) Z(b(n)) DS52 (b(n)) 1 0 1 27 1 0 25   2 0 2 14 1 1 13 2 0 12

Thus, the first part of the (11a) is proven.

• Proof of (11b)

Example 2 Let p = 3, m = 6, and m^j = 2, then the se- quence having a period of 182 becomes as follows its dis- tribution of n-bit patterns is shown in Table 6.

Let us consider the case that Z    (n) = n. Therefore,

Table 6: Bit distribution of the binary sequence 182 with p = 3, m = 6, and mj = 2. the combination of n-bit patterns except the all-zero

n Hwt(b(n)) Z(b(n)) DS182 (b(n)) 1 0 1 101 1 0 81   2 0 2 56 1 1 45 2 0 36   3 0 3 31 1 2 25 2 1 20 3 0 16

patterns is given as follows:

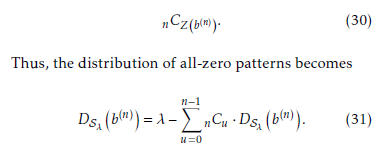Thus, the distribution of all-zero patterns becomes

Thus, the second part of the (11b) is proven. In addi- tion, the theorem in (11) is also proven.

4. Result and Discussion

This section explains the distribution of bit patterns in the binary sequence which generated over the sub extension field based on some experimental results. Then, a comparison between the binary sequence de- fined over the sub extension field and our previous geometric sequence [13] also introduces in terms of the distribution of bit patterns property. Here, H_wt denotes the hamming weight.

4.1. Experimental  Results

Let us consider the distribution of bit patterns in the binary sequence, introduced in this paper which gen- erated over the sub extension field in the following examples.

Example 1 Let p = 5, m = 4, and m^j = 2, then the se- quence having a period of 52 becomes as follows its distri- bution of n-bit patterns is shown in Table 5.

Example 3 Let p = 7, m = 9, and m^j = 3, then the se- quence having a period of 235986 becomes as follows its distribution of n-bit patterns is shown in Table 7.

 Table  7:   Bit  distribution  of  the  binary  sequence    235986  with p = 7, m = 9, and mj = 3.

n	Hwt(b(n))	Z(b(n))	DS235986 (b(n))
1	0	1	118337
	1	0	117649
2	0	2	59341
	1	1	58996
	2	0	58653
3	0	3	29757
	1	2	29584
	2	1	29412
	3	0	29241

4.1.1. Observation

It was found that the experimental results explicitly support the (11). In addition, the number of appear-

S₅₂ = {01001101000000101011110011

10110010111110010100001100}.

(32)

ance of each bit pattern is related to the number of ze- ros contained in each bit pattern. Moreover, D_S (b⁽ⁿ⁾)

increases in proportion to Z(b⁽ⁿ⁾). To confirm this, let us check the Example 2 with n = 3.ununiform distribution of bit patterns. On the other hand, sequence defined over the sub extension field minimizes this difference to make it close to uniform. This comparison graphically shown in Figure 3.

Table 8: Comparison in bit distribution between the sub field binary sequence and NTU sequence -I.

n Hwt(b(n)) DS182 (b(n)) % DNTU242 (b(n)) % 1 0 101 55.49 161 66.52 1 81 44.51 81 33.48   2 0 56 30.76 107 44.21 1 45 24.72 54 22.31 2 36 19.78 27 11.15   3 0 31 17.03 71 29.33 1 25 13.73 36 14.87 2 20 10.98 18 7.43 3 16 8.79 9 3.71

(b⁽³⁾ = 101) = 3^6−(3×2) · 4³⁻¹⁻¹ · 5¹ = 20,

(b⁽³⁾ = 111) = 3^6−(3×2) · 4³⁻¹⁻¹ · 5¹ = 20.

Z(b⁽³⁾) = 2 :

DS182 DS182 DS182

(b⁽³⁾ = 001) = 3^6−(3×2) · 4³⁻²⁻¹ · 5² = 25,

(b⁽³⁾ = 010) = 3^6−(3×2) · 4³⁻²⁻¹ · 5² = 25,

(b⁽³⁾ = 100) = 3^6−(3×2) · 4³⁻²⁻¹ · 5² = 25.

Z(b⁽³⁾) = 3 :D_S    (b⁽³⁾ = 000) = 182 − (1 × 16 + 3 × 20 + 3 × 25) = 31.

4.2. Comparison With Our Previous Work

By combining the features of the M-sequence and Leg- endre sequence our previous work [13] proposed a ge- ometric sequence, namely NTU (Nogami-Tada-Uehara) sequence. According to our previous research work, NTU sequence always holds long period, low correla- tion, high linear complexity properties which are the important considerations to use any sequence in cryp- tographic applications. Another crucial consideration before utilizing them in any secure applications, is to judge the randomness of a sequence. To do so, we need to evaluate the distribution of bit patterns property in a sequence. After the experimental observation, it was found that in terms of distribution of bit patterns NTU sequence is not uniformly distributed. In other words, in case of binary NTU sequence, there is much differ- ence in appearance between the 0 and 1. To improve this drawback, instead of prime field (which used in the NTU sequence generation procedure), we focused on the sub extension field during the sequence genera- tion procedure in this research work. As a result, after utilizing the sub extension field, the distribution of bit patterns becomes close to uniform. This comparison is shown in the following tables (Table 8 and Table 9).

It should be noted that the NTU sequence is con- trolled by 2 parameters (p and m), on the other hand the sequence over the sub extension field is controlled by 3 parameters (p, m, and m^j). Therefore, it is not possible to make the comparison between these two

sequences in terms of the same length (in other words, the same period λ). The authors kept the difference as minimum as possible.

One of the most notable outcomes of this compari- son result is the NTU sequence holds higher difference in terms of the appearance between the ‘all zero’ and ‘all one’ patterns. In other words, it also confirms the

Table 9: Comparison in bit distribution between the sub field binary sequence and NTU sequence -II.

n	Hwt (b(n))	DS240200 (b(n))	%	DNTU275514 (b(n))	%
1	0	122551	51.02	156865	56.93
	1	117649	48.98	117649	43.07
2	0	62526	26.03	89637	32.53
	1	60025	24.98	67228	24.40
	2	57624	23.99	50421	18.30
3	0	31901	13.28	51221	18.59
	1	30625	12.74	38416	13.94
	2	29400	12.23	28812	10.45
	3	28224	11.75	21609	7.84
4	0	16276	6.77	29269	10.62
	1	15625	6.50	21952	7.96
	2	15000	6.24	16464	5.97
	3	14400	5.99	12348	4.48
	4	13824	5.75	9261	3.36

Recently, there are lots of considerations to use a long period pseudo-random sequence in cryptographic applications. The use of binary sequence in a stream cipher is one of the most common application. Before applying a sequence in such applications, the linear complexity and distribution of bit patterns are con- sidered as the most important properties regarding a sequence to check its randomness. Among these two, the authors observed the linear complexity property in their previous work [16] and it always holds a maxi- mum value of the linear complexity. As a continuation, the authors focused on the distribution of bit patterns in this paper. According to the comparison results, the binary sequence generated over the sub extension field holds much better (close to uniform) compared to our previous binary sequence in terms of distribution of bit patterns. Therefore, the binary sequence defined over the sub extension field can be a suitable candidate for some cryptographic applications.

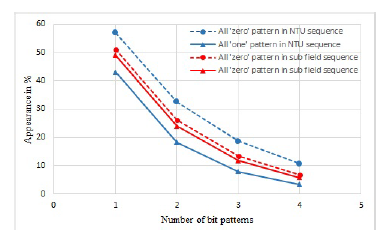Figure 3: Appearance of ‘all zero’ and ‘all one’ bit patterns in the NTU and sub field sequence.

5. Conclusion

In this paper, the authors observed the distribution of bit patterns in a binary sequence which defined over the sub extension. The number of appearances is related to the number of zeros contained in each bit pattern. Furthermore, the authors theoretically prove the distribution of bit patterns property. In addition, they also made a comparison between the binary se- quence defined over the sub extension field and our previous work on binary sequence based on distribu- tion of bit patterns property. According to the com- parison results, the binary sequence generated over the sub extension field holds much better (close to uni- form) compared to our previous binary sequence. As a future work, we would like to consider an efficient im- plementation to enhance the usability of our proposed sequence a Cryptographically Secure Pseudo Random Number Generator (CSPRNG).

Conflict of Interest

The authors declare no conflict of interest.

Acknowledgment

This work has been supported by JSPS KAKENHI Grant-in-Aid for Scientific Research

(A) Number 16H01723.

1.  J. Daemen and V. Rijmen, The Design of Rijndael, Springer-Verlag Berlin Heidelberg, Germany, 2002.
2.  Richard A. Mollin, RSA and Public-Key Cryptography, Chapman & Hall CRC, 2002.
3.  H. Cohen and G. Frey, Handbook of Elliptic and Hyperelliptic Curve Cryptography, Discrete Mathematics and Its Applications, Chapman & Hall CRC, 2005.
4.  V. Edemskiy, On the Linear Complexity of Interleaved Binary Sequences of Period 4p Obtained from Hall Sequences or Legendre and Hall Sequences, IEEE Electronic Letter, 50, 8, 604–605, 2014.
5.  M. Matsumoto and T. Nishimura, “Mersenne Twister: A 623-Dimensionally Equidistributed Uniform Pseudo- Random Number Generator”, ACM Trans. on Modeling and Computer Simulation, 8(1), 3–30, 1998. http://doi.org/10.1145/272991.272995
6.  L. Blum, M. Blum, and M. Shub, “A simple Unpredictable Pseudo-Random Number Generator”, SIAM Journal on Computing, 15(2), 364–383, 1986. http://doi.org/10.1137/0215025
7.  X. Tang and G. Gong, “New Constructions of Binary Sequences with Optimal Autocorrelation Value/Magnitude”, IEEE Trans. Inf. Theory, 56(3), 1278–1286, 2010. http:// doi.org/10.1109/TIT.2009.2039159
8.  J. S. No, H. K. Lee, H. Chung, H. Y. Song, and K. Yang, “Trace Representation of Legendre Sequence of Mersenne Prime Period”, IEEE Trans. on Inform. Theory, 42(6 PART 2), 2254–2255, 1996. https://doi.org/10.1109/18.556617
9.  J. Ren, “Design of Long Period Pseudo-Random Sequence from the Addition of m-sequences over Fp”, EURASIP Journal on Wireless Communication and Networking, 1, 12–18, 2004. http://doi.org/10.1155/S1687147204405052
10.  C. Ding, “Pattern Distributions of Legendre Sequences”, IEEE Transactions on Information Theory, 44(4), 1693–1698, 1998. http://doi.org/10.1109/18.681353
11.  B. Z. Moroz, “The distribution of power residues and nonresidues”, Vestnik Leningrad Univ. Math, 16, 164–169, 1961. (In Russian with English summary)
12.  T. Helleseth, “Maximal-length sequences”, Encyclopedia of Cryptography and Security, 2nd Ed. Springer, 5–14, 2011. https://doi.org/10.1007/978-1-4419-5906-5 359
13.  Y. Nogami, K. Tada, and S. Uehara, “Geometric Sequence Binarized with Legendre Symbol over Odd Characteristic Field and Its Properties”, IEICE Trans. on Fund. of Electronics and Computer Sciences, E97.A(12), 2336–2342, 2014. https://doi.org/10.1587/transfun.E97.A.2336
14.  Y. Nogami, S. Uehara, K. Tsuchiya, N. Begum, H. Ino, and R. H. Morelos-Zaragoza, “A Multi-value Sequence Generated by Power Residue Symbol and Trace Function over Odd Characteristic Field”, IEICE Trans. on Fund. of Electronics, Communications and Computer Sciences, E99.A(12), 2226–2237, 2016. https://doi.org/10.1587/transfun.E99.A.2226
15.  A. M. Arshad, Y. Nogami, H. Ino, and S. Uehara, “Auto and Cross Correlation of Well Balanced Sequence Over Odd Characteristic Field”, Fourth International Symposium on Computing and Networking (CANDAR), Hiroshima, Japan, 2016. http://doi.org/10.1109/CANDAR.2016.0109
16.  A. M. Arshad, T. Miyazaki, S. Heguri, Y. Nogami, S. Uehara, and R. H. Morelos-Zaragoza, “Linear Complexity of Pseudo Random Binary Sequence Generated by Trace Function and Legendre Symbol Over Proper Sub Extension Field”, Eighth International Workshop on Signal Design and Its Applications in Communications (IWSDA), Sapporo, Japan, 2017. http://doi.org/10.1109/IWSDA.2017.8095741
17.  A. M. Arshad, T. Miyazaki, Y. Nogami, S. Uehara, and R. H. Morelos-Zaragoza, “Multi-value Sequence Generated by Trace Function and Power Residue Symbol Over Proper Sub Extension Field”, IEEE International Conference on Consumer Electronics – Taiwan (ICCE-TW), Taipei, Taiwan, 2017. http://10.1109/ICCE-China.2017.7991089

(Click Here)

(Click Here)