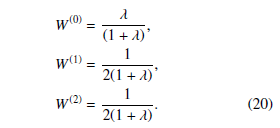1. Introduction

Recently, speech recognition systems are used in car navigation systems and smart speakers etc.. However, speech recognition can not be performed effectively in circumstances with heavy noises. Therefore, some countermeasures against surrounding noise are indispensable in such situations.

Kalman filter has been applied to many noisy circumstances as a noise cancellation method for speech signal [1],[2],[3]. This filter assumes a linear model subject to white and Gaussian noise as the system equation and the observation equation [4],[5]. Though, the extended Kalman filter (EKF) [6] can be applied to nonlinear systems, linear approximation models of nonlinear systems are required. Therefore, many improvements are necessary for the noise cancellation method to apply it to actual speech signal processing. From the above viewpoint, in our preciously reported study, a noise cancellation method was proposed by using air- and bone-conducted speech signals in the situation contaminated by non-Gaussian and non-white noises [7].

However, since the calculation of the expansion coefficients in the previous algorithm was very complicated, a simplified method is required.

On the other hand, the unscented Kalman filter (UKF) by use of unscented transformation (UT) method can be applied to nonlinear system[9]. The UT method is a technique for calculating the statistics of a random variable that has been nonlinearly transformed. The set of samples on so-called sigma points(σ-points) are chosen so that they capture the specific properties of the underlying distribution. Therefore, this method can be applied to arbitrary nonlinear systems. In our previous study, a noise cancellation method based on only air conducted speech signal has been proposed by applying the UT method [8].

In this study, a new noise cancellation algorithm based on air- and bone-conducted speech signals is proposed by considering the UT method. The relationship between airconducted speech signal and backgrand noise is expressed as an additive model based on the additive property of sound pressure. However, propagation mechanism of boneconducted speech signal is complicated and has to be considered as an unknown system in general. Therefore, a system model including unknown parameters is introduced in this study. More specifically, the sample points obtained by using the UT method are introduced. The noise cancellation algorithm is derived by use of an expansion expression of Bayes’ theorem. This method can be considered non-Gaussian properties of noises and nonlinear correlation information between the speech signal and observation. Furthermore, the validity of the proposed method is experimentally confirmed by applying it to real speech signal with noises.

2. Theory

2.1 Modeling of Air- and Bone-Conducted Speech Signals

We consider the original speech signal x_k, observed airconducted speech signal y_k and bone-conducted speech signal z_k at discrete time k. The observation y_k is contaminated by a surrounding noise v_k. According to the additive property of sound pressure, the following relationship can be established.

where the mean and variance of v_k are known. In order to derive the propagation model of the bone-conducted speech signal, the correlation information between x_k and z_k is required. However, it is difficult to obtain prior information on the unknown speech signal x_k. In this study, a new adaptive algorithm for noise cancellation is proposed by introducing a propagation model with unknown parameters between x_k and z_k as the bone-conducted speech signal model for z_k:

where w_k is a random noise (mean : 0,variance1) and a_k and b_k are unknown parameters.

2.2 Estimation Method Combined Bayes’ Theorem with UT Method

The conditional joint probability distribution of the specific signal x_k and the unknown parameters a_k and b_k is expressed by using expansion expression of Bayes’ theorem[10]. To simplify the derivation process of the estimation algorithm, σ-points and the weighting coefficients are introduced in expansion coefficients.

The conditional probability distribution of x_k, a_k and b_k is expressed as

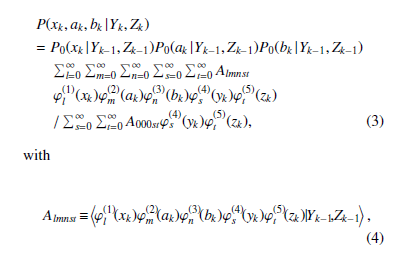where Y_k(= {y₁,y₂,…,y_k}) and Z_k(= {z₁,z₂,…,z_k}) are sets of air- and bone-conducted speech signal data up to time k. The above five functions ϕ(1)l (xk),ϕ(2)m (ak), ϕ(3)n (bk),ϕ(4)s (yk) and ϕ⁽⁵⁾_t (z_K) are orthonormal polynomials of degrees l,m,n, s and t with weighting functions P₀(x_k | Y_k−1,Z_k−1), P₀(a_k |Yk−1,Zk−1), P0(bk | Yk−1,Zk−1), P0(yk | Yk−1,Zk−1), P0(zk | Y_k−1,Z_k−1), which can be chosen as the probability functions describing the dominant part of the fluctuation. As the examples of standard probability functions, Gaussian distribution is adopted: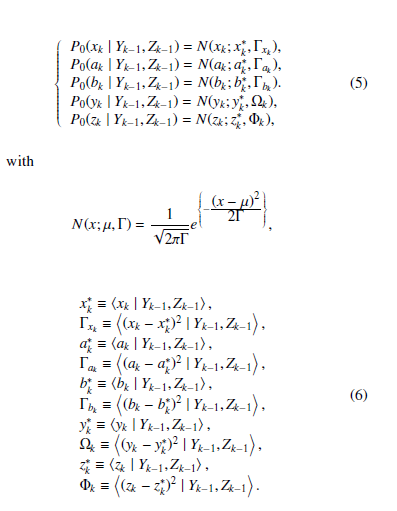

The orthonormal polynomials[11] with five weighting probability distributions in Eq. (5) are then specified as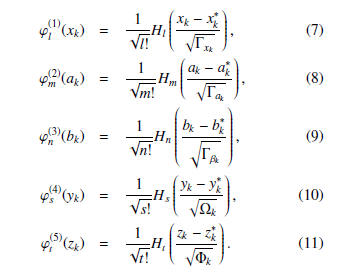

The estimates for mean and variance (i.e., conditional mean and variance) of x_k, a_k, b_k, which are the first and second order statistics, can be expressed as follows: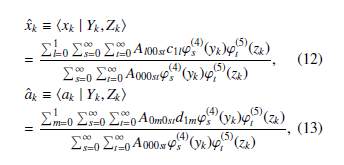

Here, the weighing coefficients W⁽ⁱ⁾ have to satisfy the normalization constraint.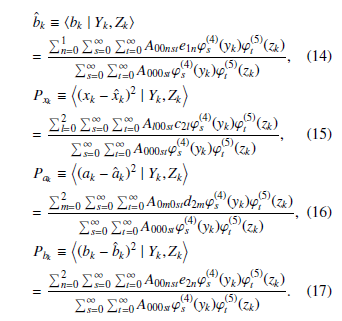

By using the UT method, the expansion coefficients de A²⁰⁰⁰¹ =W fined by (4) can be realized for arbitrary nonlinear systems.When the UT method is applied to approximate the means^{∗(i)   ∗(i)}                  A²⁰⁰⁰² = 2ΓxkΦk              2i=0 W(i) n(xk∗(i) − xk∗)2 − Γxkon(z∗k(i) − z∗k)2 − Φko, and variances of x_k, a_k, b_k, y_k and z_k, the σ-points x_k , a_k , b^∗_k⁽ⁱ⁾, y^∗_k⁽ⁱ⁾ and z^∗_k⁽ⁱ⁾ are obtained as sample points, as follows:       A10011 = √Γxk √1Ωk √Φk P2i=0 W(i)(xk∗(i) − xk∗)(y∗k(i) − y∗k)(z∗k(i) − zk∗),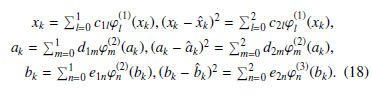

The σ-points are decided so as to obtain the approximately same mean and variance as original variables. Where λ is a regulation parameter. The weights to be used are obtained as follows:

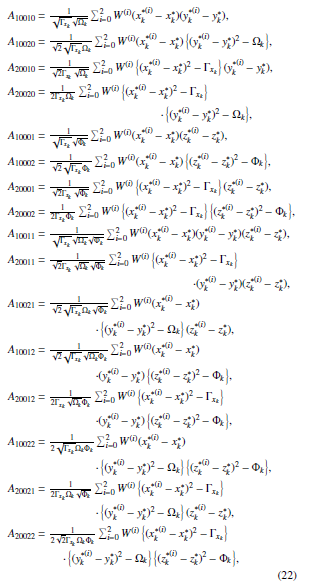
The    expansion    coefficients    of    b_k,     y_k       and    z_k(A00110, A00120, A00210, A00220, A00101, A00102, A00201, A00202, A00111, A00211, A00121, A00112, A00212, A00122, A00221, A00222) are calculated through the same manners.

After substituting (1) (2) into the definition of four parameters y^∗_k,Ω_k,z^∗_k and Φ_k in (6), the following expressions can be derived.

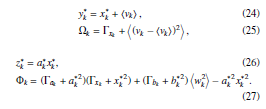In order to derive the predicted values of the speech signal x_k and the unknown parameters a_k, b_k, the time transition of the speech signal x_k is expressed as follows.

The state estimation algorithm with expansion coefficient

A_lmnst reflecting linear and nonlinear correlation information among variables and statistics of non-Gaussian noise is completed.

3. Experiment

In order to confirm the validity of the proposed noise cancellation algorithm, we compared it with the method using only the air-conducted speech signal. The compared method was derived by considering the following conditional probability distribution.

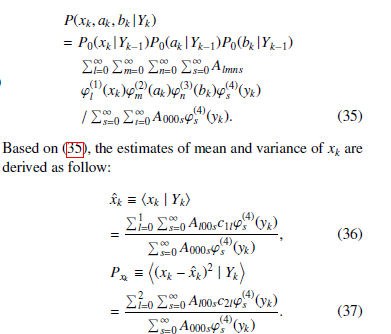Male and female speech signals were used in the experiment. The speech signal data were measured in the anechoic chamber in the acoustic laboratory. The observed speech signal are contaminated with the white noise, the pink noise and the machine noise respectively. The spectra of these noises are shown in Figures 1-3. Furthermore, the observation data of air-conduced speech signal were created by mixing noises with speech signal on a computer.

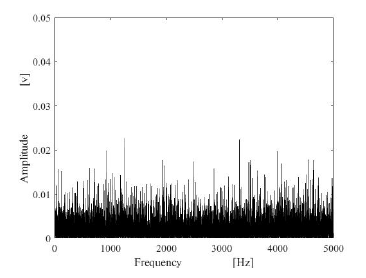Figure 1: Spectrum of white noise.

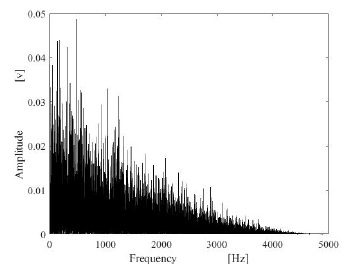Figure 2: Spectrum of pink noise.

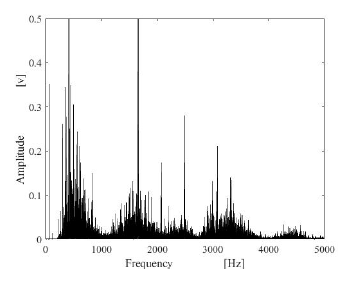Figure 3: Spectrum of machine noise.

Table 1 shows the specifications of the personal computer for signal processing in the experiment. The signal processing time for speech signal of about 3.5 seconds in length was from 0.5 to 0.8 seconds.

Table 1: The specifications of the personal computer.

	Specification
PC	Dell Vostro 3650
CPU	Intel Core i7-6700 @ 3.40GHz
MEMORY	8.00G
OS	Win 10 Pro 64bit

As an evaluation method of estimation result, the Root Mean Square Error (RMSE) and Performance Evaluation Index (PEI) are adopted.

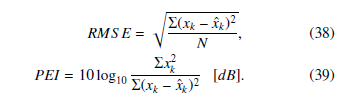As the RMS Error is smaller value, the better estimation result is obtained. On the other hand, the larger the PEI is, the better the estimation is. Table 2 and Table 3 show the results for the male speech signal and a female speech signal respectively. In the cases of lower noises, almost the same estimation results are obtained in the proposed method and the compared method. On the other hand, in the case of higher noises, the proposed method obtains better results than the compared method. Furthermore, in comparison with our previous method [7] with complicated algorithm, almost the same accurate estimation results are obtained as the proposed method. Therefore, the superiority of the proposed method adopting the simplified algorithm could be confirmed.

Table 2: Comparisons of RMSE and PEI for a male speech signal.

• white noise

	Proposed method		Compared method
S/N	RMSE	PEI	RMSE	PEI
1/1	0.0160	6.8438	0.0163	6.7057
1/2	0.0225	3.8693	0.0269	2.3286
1/3	0.0267	2.4111	0.0450	-2.1282
1/4	0.0330	0.5615	0.0838	-7.5301
1/5	0.0480	-2.6982	0.1338	-11.6004

• pink noise

	Proposed method		Compared method
S/N	RMSE	PEI	RMSE	PEI
1/1	0.0192	5.2693	0.0207	4.6124
1/2	0.0281	1.9414	0.0345	0.1846
1/3	0.0322	0.7773	0.0626	-4.9946
1/4	0.0419	-1.5062	0.0823	-7.3776
1/5	0.0669	-5.5803	0.1334	-11.5703

• machine noise

	Proposed method		Compared method
S/N	RMSE	PEI	RMSE	PEI
1/1	0.0238	3.4024	0.0272	2.2381
1/2	0.0313	1.0116	0.0489	-2.8538
1/3	0.0399	-1.0931	0.0767	-6.7613
1/4	0.0586	-4.4310	0.1080	-9.7397
1/5	0.0686	-5.8003	0.1409	-12.0497

Some of the waveform summarized in Tables 2 and 3 are shown in Figures 4-23. Figures 4 and 14 show the original speech signals of male and female, respectively. Figures 5, 8, 11, 15, 18 and 21 show the speech signals contaminated by noises with amplitude of 3 times larger than the original signals. The estimated results by using of proposed method are shown in Figures 6, 9, 12, 16, 19 and 22. On the other hand, the comparison results are shown in Figures 7, 10, 13, 17, 20 and 23. In the cases of contaminated by white noise and pink noise, the better results are obtained by the proposed method than the compared method.

Table 3: Comparisons of RMSE and PEI for a female speech signal.

• white noise

	Proposed method		Compared method
S/N	RMSE	PEI	RMSE	PEI
1/1	0.0134	4.8382	0.0104	7.0371
1/2	0.0159	3.3213	0.0160	3.2779
1/3	0.0180	2.2390	0.0195	1.5406
1/4	0.0198	1.4447	0.0273	-1.3608
1/5	0.0260	-0.9548	0.0457	-5.8342

• pink noise

	Proposed method		Compared method
S/N	RMSE	PEI	RMSE	PEI
1/1	0.0136	4.656	0.0128	5.2366
1/2	0.0176	2.4293	0.0211	0.8777
1/3	0.0231	0.0790	0.0271	-1.297
1/4	0.0241	-0.2875	0.0374	-4.1092
1/5	0.0264	-1.0874	0.0510	-6.8009

• machine noise

	Proposed method		Compared method
S/N	RMSE	PEI	RMSE	PEI
1/1	0.0147	3.9846	0.0168	2.8276
1/2	0.0207	1.0503	0.0237	-0.1545
1/3	0.0293	-1.9655	0.0499	-6.6083
1/4	0.0456	-5.8243	0.0553	-7.5024
1/5	0.0425	-5.2075	0.0660	-9.0326

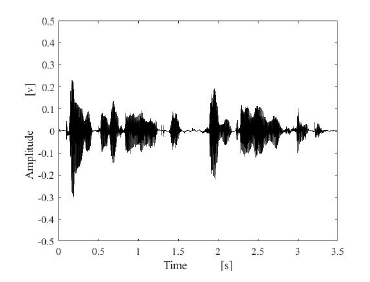Figure 4: Original male speech signal

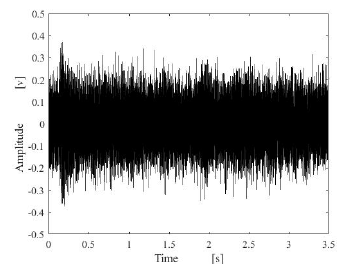Figure 5: Male speech signal containing a white noise

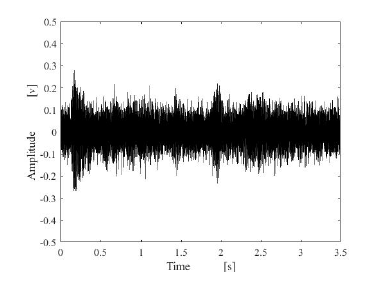Figure 7: Estimated results by using compared method.

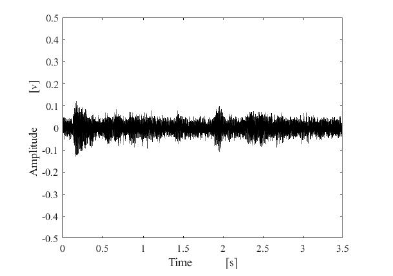Figure 6: Estimated results by using proposed method.

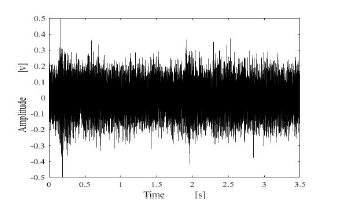Figure 8: Male speech signal containing a pink noise

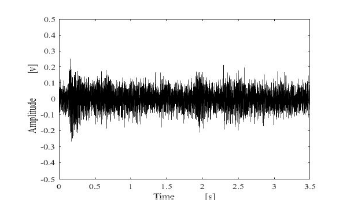Figure 9: Estimated results by using proposed method.

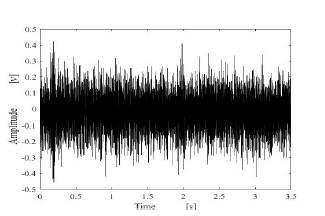Figure 11: Male speech signal containing a machine noise

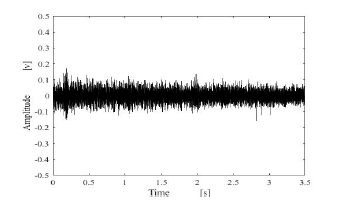Figure 12: Estimated results by using proposed method.

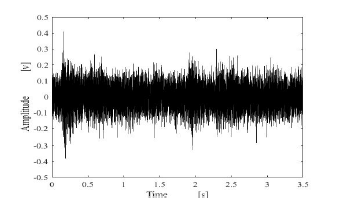Figure 10: Estimated results by using compared method.

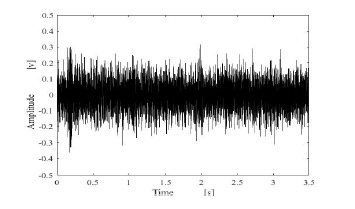Figure 13: Estimated results by using compared method.

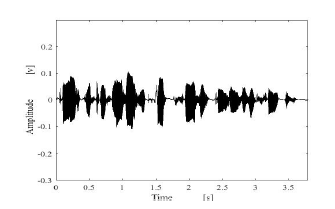Figure 14: Original female speech signal

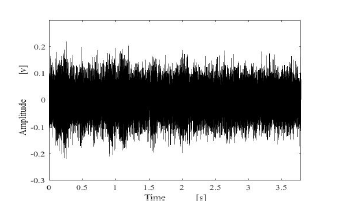Figure 15: Female speech signal containing a white noise

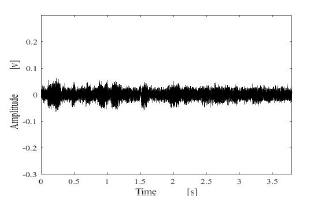Figure 16: Estimated results by using proposed method.

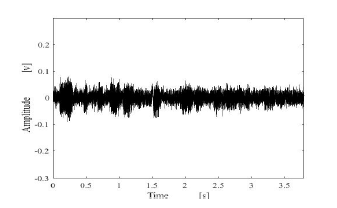Figure 17: Estimated results by using compared method.

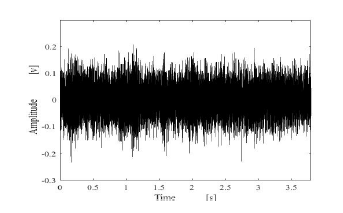Figure 18: Female speech signal containing a pink noise

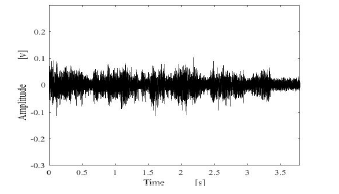Figure 19: Estimated results by using proposed method.

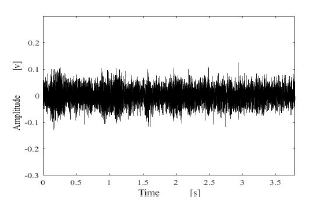Figure 20: Estimated results by using compared method.

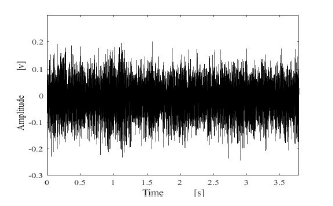Figure 21: Female speech signal containing a machine noise

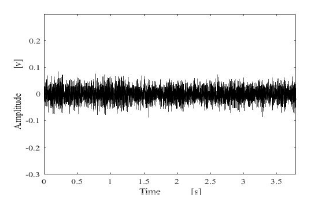Figure 22: Estimated results by using proposed method.

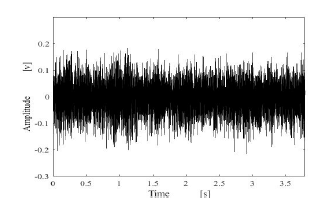Figure 23: Estimated results by using compared method.

4. Conclusion

In this paper, a new method to suppress noise for speech signal has been proposed, which is applicable to actual environment with non-Gaussian and non-white noises. The aim of the proposed method is to improve the accuracy of estimation by using air- and bone-conducted speech signals.

The proposed method considered σ-points of not only x_k but also unknown parameter a_k, b_k and observation values y_k, z_k. Moreover, this study has proposed a method including the higher order correlation information between σ-points. Our algorithm has been realized by utilizing the Bayes’ theorem as the fundamental principle of estimation and UT method using σ-points. Application of our algorithm has been made to real speech signal contaminated by noises. It has been revealed by experiments that better estimation results could be obtained by the proposed algorithm as compared with the method without using bone-conducted speech signal. However, we have not tried to apply the proposed algorithm to real speech recognition by use of a voice recognition software. Therefore, by applying the algorithm to speech recognition system, the effectiveness of the theory has to be confirmed experimentally.

The proposed approach is quite different from those traditional standard techniques. However, we are still in an early stage of development, and a number of practical problems are yet to be investigated in the future. These include: (i) Introduction of a realistic nonlinear model expressing the actual propagation characteristics of bone-conducted speech signal instead of the simple model in (2). (ii) Consideration of higher order expansion coefficients A_lmnst (l,m,n, s,t = 3), in the estimation algorithm. (iii) Selection of an optimal point to put the sensor to measure the bone-conducted speech signal.

1.  M. Gabrea, E. Grivel, and M. Najim, “A single microphone Kalman filter-based noise canceller”, IEEE Signal Process. Lett., 6 (3), 55-57, 1999.
2.  W. Kim, and H. Ko, gNoise variance estimation for Kalman filtering of noisy speech”, IEICE Trans. Inf. and Syst., E84-D (1), 155-160, 2001.
3.  N. Tanabe, T. Furukawa, and S. Tsuji, “Robust noise suppression algorithm with the Kalman filter theory for white and colored disturbance”, IEICE Trans. Fundamentals, E91-A (3), 818-829, 2008.
4.  R. E. Kalman, ”A new approach to linear filtering and prediction problems”, Trans. ASME, Series, D, J. Basic Engineering, 82 (1), 35-45, 1960.
5.  R. E. Kalman and R. S. Buch, ”New results in linear filtering and prediction theory”, Trans. ASME Series D, J. Basic Engineering, 83 (1), 95-108, 1961.
6.  H. J. Kushner, “Approximations to optimal nonlinear filter”, IEEE Trans. on Automatic Control, 12 (5), 546-556, 1967.
7.  A.Ikuta, H.Orimoto and G. Gallagher, “Noise suppression method by jointly using bone- and air-conducted speech signals”, Noise Control Engr. J. 66 (6), 472-488, 2018.
8.  H.Orimoto and A.Ikuta, “Signal processing for Noise cancellation method of speech signal by using an extension type UKF”, Proceedings of SIGNAL PROCESSING algorithms, architectures, arrangements, and applications (SPA), 304-309, 2018.
9.  James V. Candy, Bayesian Signal Processing Classical, Modern, and Particle Filtering Methods, Wiley-IEEE Press, 2009.
10.  M. Ohta and H. Yamada, “New Methodological Trials of Dynamical State Estimation for the Noise and Vibration Environmental System”, Acustica, 55 (4), 199-212, 1984.
11.  M. Ohta and T. Koizumi, “General statistical treatment of the response of a non-linear rectifying device to a stationary random input”, IEEE Trans. Inf. Theory, 14 (4), 595-598, (1968).

(Click Here)

(Click Here)