1. Introduction

Music genre classification is used to categorize musical data into suitable categories based on shared characteristics. In the modern era, numerous musical genres are appreciated, such as blues, classical, country, disco, hip-hop, jazz, metal, pop, reggae, and rock. New technologies and globalization have been beneficial for the evolution of music, leading to the emergence of world music. These developments have increased research interest in music information retrieval (MIR), a field of automatic music management including music recommendation [1], music mood classification [2], and musical instrument classification [3]. As musical genres are most commonly used to manage music databases, a previous study investigated the extraction of audio features and techniques for classifying musical genres [4, 5, 6, 7]. However, genre classification has remained a challenge[8, 9], as it requires systems that are capable of performing automatic grouping [10] and querying retrieving data from large a music data set [8]. The identification of commonalities between genres requires feature extraction [11]. In the case of audio files, combinations of relevant features are used for modeling the musical genre [4]. These features may include timbral texture, rhythmic content, and pitch content [12]. Musical genres have been modeled using different features including short-term Mel-frequency cepstral coefficients (MFCCs) [13, 14], and Daubechies wavelet coefficient histograms (DWCHs), depending on the required application. Features are selected to improve performance and accuracy [15]. Achieving optimal feature selection and extracting appropriate features and dimensions of the features reduction are very challenging tasks [16, 17]. There are many different approaches that have been proposed to classify music genre, such as data mining [18, 19], deep learning strategy [20, 21, 22, 23, 24], and machine learning stretegies such as hidden Markov model, AdaBoost, and support vector machine [25, 26, 27, 28, 29, 30, 31, 32, 33, 34].

In addition to the above, musical genre classification problems can be solved with constant evolutionary algorithms [35]. Among them, a genetic algorithm (GA) based optimization has become a widely used approach for optimizing the selection of relevant features [36, 37, 38, 39, 40].

Among the several methods developed for musical genre classification, the performance of classification algorithms has become the benchmark [41]. In this paper, we propose a model for musical genre classification using low-level time and frequency-domain features for short and mid-term feature extraction. In this model, feature extraction is performed using a GA, and musical genre classification is conducted using a range of machine learning algorithms, including the K-Nearest Neighbor (KNN) [42], Nave Bayes Classifier (NBC) [43], and the Support Vector Machine (SVM) [25] were used for music genre classification. In the performance evaluation, it was found that the GA-based feature selection strategy can improve the F-measure rate from 5% to 20% for the KNN, NBC and SVM-based algorithms. In addition, the proposed support vector machine genetic algorithm (SVMGA) algorithm can exactly better than other comparison algorithms

The remainder of this paper is organized as follows. Section 2 provides background information and discusses related studies. The proposed algorithm is presented in Section 3, and its performance is evaluated in Section 4. Finally, the conclusions and future research are presented in Section 5.

2. Literature review

The primary challenge in genre identification is selecting features for extraction from audio data [8]. Audio data comprise a series of samples that together represent an audio signal. Classification cannot simply be applied to the audio samples. In previous studies, audio analysis has been prominently performed by extracting numerical values for representative features. In music signals, these features correspond to primary dimensions such as pitch, rhythm, harmony, melody, timbre, and spatial location. Low-level features, such as temporal, energy, and spectral features, are some of the most prominently used features in sound signal analysis. In audio signal analysis, low-level features are generally extracted from the time and frequency domains [44]. Moreover, 11 sets of low-level time- and frequency-domain features are prominently used.

2.1. Time-domain audio features

In general, time-domain features are directly extracted from samples of audio signals. The features include short-term energy, short-term zero-crossing rate, and entropy. These features provide a simple approach to analyzing audio signals, and combining these features with sophisticated frequencydomain features is generally essential.

• Energy: The sum of squares of signal values, normalized by the respective frame length.
• Zero-Crossing Rate: The rate at which the sign of the signal changes within a particular frame.
• Entropy of Energy: The entropy of the normalized energies of subframes, which can be interpreted as a measure of abrupt changes in the signal.

2.2. Frequency-domain audio features

The discrete Fourier transform (DFT) is extensively used in audio signal analysis, because it provides a convenient representation of the frequency content distribution of a signal as a sound spectrum. Numerous audio features are based on the DFT of a signal. These are termed frequency-domain (or spectral) audio features.

• Spectral Centroid: The center of gravity of a spectrum.
• Spectral Spread: The second central moment of a spectrum.
• Spectral Entropy: The entropy of the normalized spectral energies for a set of sub-frames.
• Spectral Flux: The squared difference between normalized magnitudes of the spectra of two successive frames.
• Spectral Rolloff: The frequency below which 90% of the magnitude distribution of a spectrum is concentrated.
• MFCCs: MFCCs are used to capture short-term, spectral-based features. The logarithm of the amplitude spectrum based on a short-time Fourier transform is derived for each frame. Frequency bins are then grouped and smoothed using Mel-frequency scaling to ensure that they agree with predetermined concepts. MFCCs are generated by decorrelating Mel-spectral vectors by using a discrete cosine transform.
• Chroma Vector: A chroma vector is a 12-element representation of spectral energy, wherein bins represent 12 equal-tempered pitch classes of Western music (semitone spacing).
• Harmonic: Harmonic features represent beats, and the harmonic ratio and fundamental frequency are two harmonic features.

Although studies have been conducted on music genre classification, the most accurate results have been achieved using the GTZAN dataset. A comprehensive set of features was proposed for the direct modeling of music signals [4]. When these features were employed for genre classification by using KNNs and Gaussian Mixture models (GMMs), an accuracy rate of 61% was achieved. A novel feature extraction method was proposed for musical genre classification, wherein DWCHs are combined with machine learning classification algorithms, including SVMs and linear discriminant analysis [14]. An accuracy of 78.5% was obtained with this method. Feature integration methods and late information fusion were examined in a previous study [12], by using majority voting for classification of all short-time features. A novel feature integration technique using an autoregressive (AR) model was proposed. This approach was reported to exhibit superior performance to that obtained by the use of mean variance features. Another study [45] addressed musical genre classification from a multilinear perspective. Multiscale spectro-temporal modulation features were extracted on the basis of an auditory cortical processing model, which provided an accuracy of 78.2%. Nonnegative matrix factorization was used to obtain a novel description of the timbre of musical sounds[13]. A spectrogram was factorized, which provided a characteristic spectral analysis. Gaussian Mixture Models were then applied, to achieve a reported accuracy of 74%. An ensemble approach [37], involving the use of multiple feature vectors and time and space decomposition strategies was also reported in a previous study. In the study, time decomposition was performed using feature vectors, which were extracted from music segments obtained from the beginning, middle, and end of the original signal. The study also employed four machine learning algorithms, namely NBC, decision trees, SVMs, and multilayer perceptron (MLP) neural nets, which provided a maximum accuracy of 65.06%. In an alternative approach [46], a method based on the classification accuracy of an SVM classifier was proposed for selecting training instances. These instances comprised feature vectors representing short-term, low-level characteristics in an audio signal. This method was reported to provide an accuracy of 59.6%. An invariance of MFCCs to musical key and tempo was explored in a previous study[47]. The study indicated that MFCCs encode both timbral and key information. An accuracy of 69.3% was achieved by applying GMMs. The acoustic signal feature can be derived using a mathematical model that represents the acoustic signal [39]. In this approach, features were selected using a GA. Classification was then performed by generating an adjusted KNN classifier. The reported accuracy was 67.6%. In a previous study, a subspace cluster analysis process was used to automate the construction of a classification tree[48]. Experimental results validated the tree-building algorithm, and the study provided a new research direction for automatic genre classification. Several machine learning algorithms were employed, such as KNNs, J48, logistic regression (LOG), LibSVM with a radial basis function kernel, MLP neural networks, and sequential minimal optimization (SMO) SVM with a polynomial kernel. This method was reported to achieve an accuracy of 72.9%.

Another study[49] proposed automatic musical genre classification by using spectral, time-domain, tonal, rhythmic, sound effect, and high-level descriptors. An analysis was conducted using KNNs, an SVM, and a GMM, with a resulting accuracy of 79.7%.

3. Methods

3.1. Feature extraction

Feature extraction is a crucial step in audio analysis, because it is also required in other pattern recognition and machine learning tasks. Extraction is performed in the following two steps: short- and mid-term processes. In short-term feature extraction, the input signal is divided into brief windows (or frames), and the number of features is computed for each frame, generating a sequence of short-term feature vectors from the entire signal. In mid-term extraction, statistical analysis is generally applied to these short-term feature sequences to obtain the signal. Several statistics, including mean, median, standard deviation, standard deviation by mean, max, and min, are derived for each short-term feature sequence. The data are then normalized to avoid the introduction of anomalies and minimize redundancy

3.2. Machine learning methods (naive Bayes classifier (NBC), K-nearest neighbor (KNN), support vector machine (SVM)) combined with genetic algorithm (GA)

Fig. 1 shows the system design. GA optimization is combined with the KNN, NBC, and SVM learning methods.

The fitness function uses the largest f-measure value derived using machine learning, and is evaluated using 10-fold crossvalidation. The system then derives the maximum fitness.

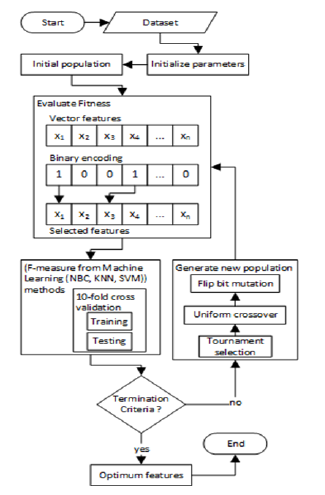Figure 1: Machine learning methods (NBC, KNN, SVM) combined with GA

• The dataset is a feature vector containing normalized data. All necessary parameters are initialized. The initial population is generated and encoded in binary {0,1}. Individual solutions are randomly generated to form the initial population P = {S₁,S₂,S₃,·· ,S_n}; S₁ = S₂ = S₃ = ··· = S_n = {G₁,G₂,G₃,··· ,G_n}. Here S is a solution and G_n represents features, where G_n ∈ {0,1}; feature labeled 0 are not used, whereas those labeled 1 are used.
• The fitness of each solution (S) is evaluated using the highest f-measure value for musical genre classification conducted through the KNN, NBC, and SVM learning methods, following the 10-fold cross-validation method. The highest fitness value indicates the optimal classification result.
• After all fitness values are obtained, tournament selection is used to select parents. This prominently used method probabilistically selects genomes for recombination; the selection is based on fitness. The algorithm randomly selects genomes from the population to compete in tournaments of user-selected size T. The genome with the highest fitness value in each tournament is selected for recombination.
• A uniform crossover is primarily used for problems, wherein elements in the genome are independent of each other. In this case, the locations of genes relative to each other in the genome do not influence fitness. The probability of crossover per gene is set by the user. The uniform crossover process generates a solution in the (t+1)th generation by randomly selecting genes from each of the winners, corresponding to the relevant locations.
• A matrix of 1s and 0s is generated, and mutation is applied individually to each element. The probability of mutation per gene is set by the user. The selected values are interchanged such that 1s become 0s (and vice versa).
• Crossover and mutation then generate a new population (solution), whose fitness value is reevaluated.
• The process is stopped when the required criteria are satisfied; otherwise, the fitness is reevaluated.
• The GA then identifies the optimal solution, which in this case is a set of optimal features.

3.3. Evaluation

For the proposed method, selected audio files were used as validation data in this study. Each file was tested through cross-validation for ensuring its allocation to the accurate class. The result was presented in a confusion matrix summarizing accurately and inaccurately classified cases. The f-measure value was calculated from the matrix to determine the optimal classification. The harmonic mean of precision and recall was used as the f-measure value, with the highest f-measure value indicating the most accurate classification.

4. Experimental results

4.1. Environment setting

The data used in this study comprised instrumental music files from the GTZAN genre collection datasets[4]. The data were obtained from the following source:¹. The dataset comprised 1000 30-s music files in an audio format at a sampling rate of 22050 Hz in 16-bit mono. Samples were classified into the following 10 musical genres: blues, classical, country, disco, hip-hop, jazz, metal, pop, reggae, and rock. The raw data were obtained from audio data files. The data were preprocessed by converting the data files into a numerical form before the execution of feature extraction. A total of 11 sets of low-level time- and frequency-domain features were extracted.

All experiments were performed over 15 independent runs and conducted using MATLAB 2016b with the parallel toolbox. The experiments were conducted on a standard laptop with an Intel i5-3320M 2.60-GHz CPU and 4-GB RAM.

4.2. Without feature selection

4.2.1. Experimental results obtained using KNN

Table 1: Results obtained by KNN without feature selection Table 2: Results Obtained by NBC without Feature Selection Fbest                          Fworst                          Fmean                           Fsd Value      time(s) Value      time(s) Value      time(s) Value    time(s) 59.1%        9.07 56.8%        8.90 58.0%        8.93 0.6%           0.08 Table 3: Results Obtained by SVM without Feature Selection Fbest                          Fworst                          Fmean                             Fsd Value      time(s) Value      time(s) Value      time(s) Value        time(s) 77.0%       14.37 75.3%       12.36 76.2%       13.16 0.005%          1.69

As presented in Table 1, the KNN method performed data execution in less than 1 second in all experiments, with the F-measure mean (Fmean) time being 0.87s and a standard deviation (Fsd) time of 0.03s, yielding an Fmean of 66.2%. The difference between the best F-measure (Fbest) and the worst F-measure (Fworst) was not significant, at 1.4%. Moreover, the Fsd value was negligible, at 0.5%. For classification, the f-measure range was 65.5% to 66.9%. In the results shown, the performance of KNN is less than 70%, but very quickly classifies the music data, owing to the fact that KNN does not need the training process..

4.2.2. Experimental results obtained using NBC

Table 2 shows the NBC results. The Fmean time for data execution was 8.93s, with an Fsd time of 0.08s for each experiment and an Fmean of 58%. The difference between Fbest and Fworst was not significant, at 2.3%. Fsd was also very small, at 0.6%. For classification, the f-measure range was approximately 56.8% to 59.1%. In the results show, the performance of NBA is less than 60% and even slower than the KNN.

4.2.3. Experimental results obtained using SVM

Table 3 shows the SVM results. For all experiments, the Fmean and Fsd times for data execution were 13.16 and 1.69 s, respectively, with an Fmean of 0.762 (76.2%). The difference between Fbest and Fworst was 0.017 (1.7%), which was nonsignificant. Moreover, the Fsd value was 0.005 (0.5%), which was negligible. The f-measure range for classification was 0.7530.770 (75.3%77.0%).

4.3. With GA feature selection

4.3.1. Parameter Setting

The previous result shows that KNN is the best algorithm for F-measure and computation times. Thus, in this section we will try to import the GA-based feature selection strategy into these three algorithms. The basic parameter settings of all experiments are listed in Table 4. All experimental results are collected from 15 independent runs, each of 100 iterations.

Table 4: GA parameter settings

Parameter	Setting
iteration	100
population	15
crossover rate	90%
mutation rate	1%
selection operator	tournament
crossover operator	uniform
tournament size	2
Number of features	204

4.3.2. Experimental results obtained using KNNGA

From Table 5, it can be seen that KNN-GA required less than

5s for data execution in each experiment. The Fmean time of 4.74 s and Fsd time of 0.43 s gave an Fmean of 71.3%. The difference between Fbest and Fworst was not significant, at 1.2%. Fsd was also very small, at 0.3%. For classification, the approximate f-measure range was 70.8% to 72%. . In summary, we found that the GA-based feature selection will improve the 5% F-measure rates with the KNN approach.

4.3.3. Experimental results obtained using NBCGA

From Table 6 it can be seen that, for data execution, the NBC-GA required a fairly long Fmean time of 61.46 s. With the Fsd time of 8.50 s for each experiment, this gave an Fmean of 66.8%. The difference between Fbest and Fworst was not significant, at 0.9%. The Fsd was also insignificant, at 0.3%. The f-measure range for classification was approximately 66.4% to 67.3%. In summary, we found that the GA-based feature selection will improve the 10% F-measure rates with the NBC approach.

4.3.4. Experimental results obtained using SVMGA

As can be seen from Table 7, SVM-GA required a fairly long Fmean time for data execution, of 125.614s. With an

Fsd time of 44.29s from each experiment, the Fmean was

79.5%. The difference between Fbest and Fworst was not significant, at 1.1%. The Fsd was also very small, at 0.3%. The f-measure range for classification was approximately

79.0% to 80.1%. In summary, we found that the GA-based feature selection will improve about the 3-5% F-measure rates with the SVM approaches.

4.3.5. Convergence Rates of KNN-GA, NBC-GA, and SVM-GA

The graphs in Figs 2, 3, and 4 reach steady state because they include a stop criterion at the 100th iteration when the process ended.

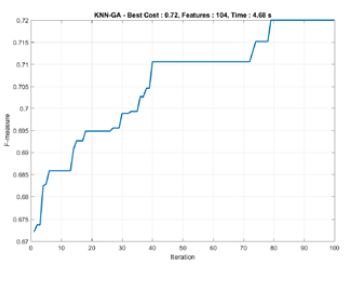Figure 2: Convergence rates of KNN with Genetic Algorithm

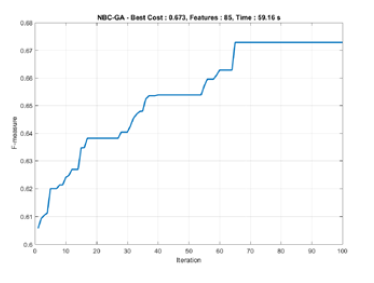Figure 3: Convergence rates of NBC with Genetic Algorithm

Table 5: Results Obtained by KNN with Feature Selection Fbest                          Fworst                          Fmean                             Fsd Value      time(s) Value      time(s) Value      time(s) Value        time(s) 72.0%        4.68 70.8%        4.66 71.3%        4.74 0.003%          0.43 Table 6: Results Obtained by NBC with Feature Selection Table 7: Results Obtained by SVM with Feature Selection Fbest                          Fworst                          Fmean                           Fsd Value      time(s) Value      time(s) Value      time(s) Value    time(s) 80.1%      121.19 79.0%      123.46 79.5%      141.05 0.3%         44.29

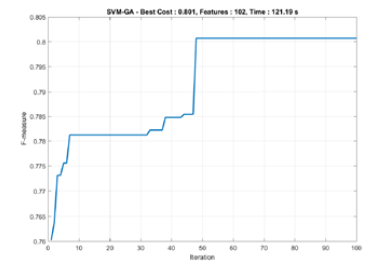Figure 4: Convergence rates of SVM with Genetic Algorithm

4.4. Comparison of F-measure values

The performance is assessed based on Eq. 1.

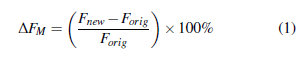Here, ∆F_M denotes the improvement of the F-measure values, ∆t_avg denotes the improvement of computation time, F_new denotes the F-measure values of the KNN, NBA, and SVM algorithm performing the genetic algorithm feature selection, and F_orig denotes the KNN, NBA, and SVM algorithms without performing any feature selection strategy, and t_avg is the computation time in seconds.

Table 8 shows that the average increase in the Fmean value was approximately 7.24% for KNN-GA, approximately 13.27% for NBC-GA, and 4.23% for SVM-GA. However, in order to perform the feature selection strategy, the computation time was increased to between 500% and 871%. In summary, the feature selection increases the quality of the solution, but with a massive increase in computation time, especially with SVM-GA, which requires spending more than 10 times the computation time..

4.5. Comparison of results in this study with those in previous studies

Previous results showed the ability of a GA to improve the quality of result classification by reducing features. The existing algorithm performs poor quality classification (approximate Fmean 59%66%). Moreover, by feature selection using the GA, the quality classification can be improved until Fmean is 67%80%. In this section, we compare the proposed algorithm with other algorithms to verify the performance or proposed algorithms. Table 9 compares the accuracy of different methods with our proposed algorithms, KNN-GA, NBA-GA, and SVM-GA, using the highest measure achieved by each. All studies used the same GTZAN Genre Collection Data Sets [4]. The KNN-GA method from the current study produced an Fbest value of 72%, which is better than the comparison algorithms of [4, 39, 47, 48]. The NBC-GA method produced an Fbest value of 67.3%, which exceeded that reported in [4]. The SVM-GA method produced an Fbest value of 80.1%, which exceeded previous studies. In summary, the GA combined with the SVM method can obtain a better solution than other algorithms.

5. Conclusions and Future work

In this study, automatic musical genre classification was conducted by combining GA optimization with three machine learning methods. This approach entails using low-level time- and frequency-domain features. The features are extracted using short- and mid-term processes. The optimal classification accuracy levels achieved in the study were determined to be comparable to those achieved by other stateof-the-art musical genre classification algorithms. However, the feature selection strategy will consume a massive amount of computation time. As part of our future research, we aim to investigate three aspects: 1) applying other meta-heuristic methods such as particle swarm optimization (PSO) to select low-level features; 2) combining deep-learning techniques such as CNN with a meta-heuristic algorithm to improve the accuracy of classification results; and 3) decreasing the computation time by using feature reduction mechanisms to make the algorithm perform more effectively.

Table 8: Comparison of f-measure values Measure         KNN-GA                     NBA-GA                   SVM-GA ∆FM ∆ tavg ∆FM ∆ tavg ∆FM ∆ tavg Fbest 7.08 598 12.18 552 3.87 743 Fworst 7.49 461 14.46 546 4.68 898 Fmean 7.15 444 13.17 588 4.15 971 Average 7.24 501 13.27 562 4.23 871 Table 9: Comparison with previous studies Algorithm Feature Selection Accuracy Tzanetakis et al. [4] none 61.0% Li et al. [14] none 78.5% Holzapfel et al. [13] none 74.0% Panagakis et al. [45] none 78.2% Li et al. [47] none 69.3% Karkavitsas et al. [39] Hybrid GA 67.6% Ariyaratne et al. [48] none 71.3% Martins de Sousa et al. [49] none 79.7% KNN-GA GA 72.0% NBA-GA GA 67.3% SVM-GA GA 80.1%

6. Acknowledgement

This work was supported in part by the Ministry of Science and Technology, Taiwan, R.O.C., under grants MOST 107-2218-E-992-303-.

1.  Markus Schedl. The lfm-1b dataset for music retrieval and recommendation. In Proceedings of the 2016 ACM on International Conference on Multimedia Retrieval, pages 103–110. ACM, 2016.
2.  Xiao Hu, Kahyun Choi, and J Stephen Downie. A framework for evaluating multimodal music mood classification. Journal of the Association for Information Science and Technology, 68(2):273–285, 2017.
3.  DG Bhalke, CB Rama Rao, and Dattatraya S Bormane. Automatic musical instrument classification using fractional fourier transform based-mfcc features and counter propagation neural network. Journal of Intelligent Information Systems, 46(3):425–446, 2016.
4.  G. Tzanetakis and P. Cook. Musical genre classification of audio signals. IEEE Transactions on Speech and Audio Processing, 10(5):293– 302, 2002.
5.  R Hillewaere. Computational models for folk music classification. Vrije Universiteit Brussel, 2013.
6.  D´ebora C Corrˆea and Francisco Ap Rodrigues. A survey on symbolic data-based music genre classification. Expert Systems with Applications, 60:190–210, 2016.
7.  Izaro Goienetxea, Jos´e Mar´ia Mart´inez-Otzeta, Basilio Sierra, and I˜nigo Mendialdua. Towards the use of similarity distances to music genre classification: A comparative study. PloS one, 13(2):e0191417, 2018.
8.  Z. Fu, G. Lu, K. M. Ting, and D. Zhang. A survey of audio-based music classification and annotation. IEEE Transactions on Multimedia, 13(2):303–319, 2011.
9.  Marius Kaminskas and Francesco Ricci. Contextual music information retrieval and recommendation: State of the art and challenges. Computer Science Review, 6(2):89–119, 2012.
10.  N. Scaringella, G. Zoia, and D. Mlynek. Automatic genre classification of music content: a survey. IEEE Signal Processing Magazine, 23(2):133–141, 2006.
11.  Dalibor Mitrovi, Matthias Zeppelzauer, and Christian Breiteneder. Features for content-based audio retrieval. volume 78, pages 71–150. Elsevier, 2010.
12.  A. Meng, P. Ahrendt, and J. Larsen. Improving music genre classification by short time feature integration. In Proceedings. (ICASSP ’05). IEEE International Conference on Acoustics, Speech, and Signal Processing, 2005., volume 5, pages v/497–v/500 Vol. 5, 2005.
13.  A. Holzapfel and Y. Stylianou. Musical genre classification using nonnegative matrix factorization-based features. IEEE Transactions on Audio, Speech, and Language Processing, 16(2):424–434, 2008.
14.  Tao Li, Mitsunori Ogihara, and Qi Li. A comparative study on contentbased music genre classification. In Proceedings of the 26th Annual International ACM SIGIR Conference on Research and Development in Informaion Retrieval, pages 282–289, 2003.
15.  Girish Chandrashekar and Ferat Sahin. A survey on feature selection methods. Computers & Electrical Engineering, 40(1):16 – 28, 2014.
16.  I. Vatolkin, W. Theimer, and G. Rudolph. Design and comparison of different evolution strategies for feature selection and consolidation in music classification. In 2009 IEEE Congress on Evolutionary Computation, pages 174–181, 2009.
17. Babu Kaji Baniya, Joonwhoan Lee, and Ze-Nian Li. Audio feature reduction and analysis for automatic music genre classification. In 2014 IEEE International Conference on Systems, Man, and Cybernetics (SMC), pages 457–462. IEEE, 2014.
18. Mangesh M Panchwagh and Vijay D Katkar. Music genre classification using data mining algorithm. In 2016 Conference on Advances in Signal Processing (CASP), pages 49–53. IEEE, 2016.
19.  Nimesh Ramesh Prabhu, James Andro-Vasko, Doina Bein, and Wolfgang Bein. Music genre classification using data mining and machine learning. In Information Technology-New Generations, pages 397– 403. Springer, 2018.
20.  Arjun Raj Rajanna, Kamelia Aryafar, Ali Shokoufandeh, and Raymond Ptucha. Deep neural networks: A case study for music genre classification. In 2015 IEEE 14th International Conference on Machine Learning and Applications (ICMLA), pages 655–660. IEEE, 2015.
21.  Il-Young Jeong and Kyogu Lee. Learning temporal features using a deep neural network and its application to music genre classification. In Ismir, pages 434–440, 2016.
22.  Sergio Oramas, Oriol Nieto, Francesco Barbieri, and Xavier Serra. Multi-label music genre classification from audio, text, and images using deep features. arXiv preprint arXiv:1707.04916, 2017.
23.  Yandre MG Costa, Luiz S Oliveira, and Carlos N Silla Jr. An evaluation of convolutional neural networks for music classification using spectrograms. Applied soft computing, 52:28–38, 2017.
24.  L Rafael Aguiar, MG Yandre Costa, and N Carlos Silla. Exploring data augmentation to improve music genre classification with convnets. In 2018 International Joint Conference on Neural Networks (IJCNN), pages 1–8. IEEE, 2018.
25.  Thorsten Joachims. Text categorization with support vector machines: Learning with many relevant features. In European conference on machine learning, pages 137–142. Springer, 1998.
26.  Wei Chai and Barry Vercoe. Folk music classification using hidden markov models. In Proceedings of international conference on artificial intelligence, volume 6. sn, 2001.
27.  Guodong Guo and Stan Z Li. Content-based audio classification and retrieval by support vector machines. IEEE transactions on Neural Networks, 14(1):209–215, 2003.
28. Changsheng Xu, Namunu Chinthaka Maddage, and Xi Shao. Automatic music classification and summarization. IEEE transactions on speech and audio processing, 13(3):441–450, 2005.
29.  Alexios Kotsifakos, Evangelos E Kotsifakos, Panagiotis Papapetrou, and Vassilis Athitsos. Genre classification of symbolic music with smbgt. In Proceedings of the 6th international conference on Pervasive technologies related to assistive environments, page 44. ACM, 2013.
30.  Kamelia Aryafar, Sina Jafarpour, and Ali Shokoufandeh. Automatic musical genre classification using sparsity-eager support vector machines. In Proceedings of the 21st International Conference on Pattern Recognition (ICPR2012), pages 1526–1529. IEEE, 2012.
31.  Loris Nanni, Yandre MG Costa, Alessandra Lumini, Moo Young Kim, and Seung Ryul Baek. Combining visual and acoustic features for music genre classification. Expert Systems with Applications, 45:108–117, 2016.
32.  AB Mutiara, R Refianti, and NRA Mukarromah. Musical genre classification using support vector machines and audio features. TELKOMNIKA TELKOMNIKA (Telecommunication, Computing, Electronics and Control), 14:1024–1034, 2016.
33.  Hareesh Bahuleyan. Music genre classification using machine learning techniques. arXiv preprint arXiv:1804.01149, 2018.
34.  Aldona Rosner and Bozena Kostek. Automatic music genre classification based on musical instrument track separation. Journal of Intelligent Information Systems, 50(2):363–384, 2018.
35.  B. Xue, M. Zhang, W. N. Browne, and X. Yao. A survey on evolutionary computation approaches to feature selection. IEEE Transactions on Evolutionary Computation, 20(4):606–626, 2016.
36.  Il-Seok Oh, Jin-Seon Lee, and Byung-Ro Moon. Hybrid genetic algorithms for feature selection. IEEE Transactions on Pattern Analysis and Machine Intelligence, 26(11):1424–1437, 2004.
37.  C. N. Silla Jr., A. L. Koerich, and C. A. A. Kaestner. Feature selection in automatic music genre classification. In 2008 Tenth IEEE International Symposium on Multimedia, pages 39–44, 2008.
38.  Dragan Matic. A genetic algorithm for composing music. volume 20, pages 157–177, 2010.
39.  George V. Karkavitsas and George A. Tsihrintzis. Automatic music genre classification using hybrid genetic algorithms. In Intelligent Interactive Multimedia Systems and Services, pages 323–335, 2011.
40.  Chih-Fong Tsai, William Eberle, and Chi-Yuan Chu. Genetic algorithms in feature and instance selection. Knowledge-Based Systems, 39:240 – 247, 2013.
41.  Bob L. Sturm. Classification accuracy is not enough. Journal of Intelligent Information Systems, 41(3):371–406, 2013.
42.  Muhammad Atif Tahir, Ahmed Bouridane, and Fatih Kurugollu. Simultaneous feature selection and feature weighting using hybrid tabu search/k-nearest neighbor classifier. Pattern Recognition Letters, 28(4):438–446, 2007.
43.  Jingnian Chen, Houkuan Huang, Shengfeng Tian, and Youli Qu. Feature selection for text classification with na¨ive bayes. Expert Systems with Applications, 36(3):5432–5435, 2009.
44.  Theodoros Giannakopoulos and Aggelos Pikrakis. Introduction to Audio Analysis: A MATLAB Approach. Academic Press, 1st edition, 2014.
45.  I. Panagakis, E. Benetos, and C. Kotropoulos. Music genre classification: a multilinear approach. In JP Bello, E Chew, and D Turnbull, editors, International Symposium Music Information Retrieval, pages 583 – 588, 2008.
46.  M. Lopes, F. Gouyon, A. L. Koerich, and L. E. S. Oliveira. Selection of training instances for music genre classification. In 2010 20th International Conference on Pattern Recognition, pages 4569–4572, 2010.
47.  Tom L. H. Li and Antoni B. Chan. Genre classification and the invariance of mfcc features to key and tempo. In Advances in Multimedia Modeling, pages 317–327, 2011.
48.  H. B. Ariyaratne and D. Zhang. A novel automatic hierachical approach to music genre classification. In 2012 IEEE International Conference on Multimedia and Expo Workshops, pages 564–569, 2012.
49.  J. Martins de Sousa, E. Torres Pereira, and L. Ribeiro Veloso. A robust music genre classification approach for global and regional music datasets evaluation. In 2016 IEEE International Conference on Digital Signal Processing (DSP), pages 109–113, 2016.

(Click Here)

(Click Here)