1. Introduction

Primary diagnosis of brain tumors is extremely significant, because it can save lives. Accurate segmentation of brain tumors is also important, as it can help medical personnel in the planning of treatment and intervention. Manual segmentation of tumors requires a long period of time, even for a qualified specialist. Fully automated segmentation and quantitative analysis of tumors, therefore, are highly beneficial maintenance. However, it is also very difficult due to the large variety of anatomical structures and low contrast of current imaging techniques that create the distinction between normal and tumor regions. The main objective of our research is to create a trustworthy procedure detection of tumors of a multimodal MRI record based on a controlled machine study the methods using a data set containing MICCAI Brats images with ground truth, provided by human experts.

In this article we propose fusion-based results binding (result fusion) method for image enhancement and combination of adaptive k-means clustering and morphological operation for tumor segmentation and reliable detection system are proposed. In MRI image enhancement, the definition of results fusion                      method is fusion the filtered results of median filter and wiener filter. We emphasized on the results of median filter and wiener filter. Median filter made the original image to be more sharpening and wiener filter made the image to be more smoothness. Segmentation of brain tumors is extremely significant, because it can save lives. Accurate segmentation of brain tumors is also important.

By fusion of these results, we got more sharpening and more smoothness image in this research. This is one of contribution for our article. Second is adaptive K-mean clustering is used like as segmentation method in this article. And then, we proposed the usage of opening and closing in morphological operation in this research. Second contribution of our article is the combination of clustering method and modified morphological operation to segment the MRI images. The experimental results will be discussed in the next chapters. This article is implemented with 6 chapters. Chapter 1 is Introduction, chapter 2 is state of the art, chapter 3 is theory background, chapter 4 is material and method, chapter 5 is experiments and chapter 6 is conclusion of the paper. This article is extended version of our paper in PDCAT’17 conference with the title of “MRI images Enhancement and Brain Tumor Segmentation” [1]. In this article, more datasets were tested and presented about the kernel of filters, discussed about the proposed system details.

2. State of The Art

2016. Jeevakala and B. Therese described the paper title with “Non Local Means Filter Based Rician Noise Removal of MR Images” in 2016. In this paper, the authors proposed a combination of NLM and stationary wavelet transform (SWT) with adaptive thresholding to remove Rician noise and preserve structural information of edges. The proposed noise elimination algorithm will be useful for the subtle analysis of tissue / organ images [2]. M. N. Nobi and M. A. Yousuf proposed the paper title with “A New Method to Remove Noise in Magnetic Resonance and Ultrasound Images”. The proposed method is compared with a smoothing, medium and midpoint filter using quantitative parameters such as PSNR, SNR, and RMSE. The smoothing filter shows better results, but it is painful because of the blurring effect. In the medium filtering technique, it is considered that each pixel calculates the average and all the pixels are replaced by the calculated average. Therefore, the affected pixels are taken into account to calculate the average, and the unaffected pixels are replaced by this calculated average [3]. B. Shinde and AR Dani have announced a “Noise Detection and Removal Filtering Techniques in Medical Images” in 2012. In this experiment, various medical images, such as MRI, cancer, X-ray, brain, etc. All these medical images, after detection of Gaussian noise, use median filtering techniques to remove noise. The results they have achieved are more useful and found useful for general practitioners to easily analyze the patient’s symptoms [4].
2017. Mihailova et al. (2016) proposed the paper “Comparative Analysis Various Filters for Noise Reduction in MRI Abdominal Images. Gaussian noise is random noise, and has a normal distribution of the probability density function (also known as a Gaussian distribution). Rician noise is not additive noise, but it depends on the data. The median filter performs better than the Gaussian filter. Wiener filter works best, but the most significant results they get from the seismic pulse and especially the wavelet of the homomorphic filter [5]. The next paper is “Propagated Image filtering” and it was presented by J.H.R. Chang et al (2015). In this document, authors proposed a propagation filter as a local filtering operator with the objective of smoothing images while maintaining the context information of the image. Authors also propose technologies when propagation filtering is related to the propagation of beliefs and a greater acceleration of the filtering process is required. In the experiments, the propagation filter was applied to various applications, such as image noise reduction, smoothing, melting, high dynamic range (HDR) compression. Finally, several applications Computer vision and graphics have verified the effectiveness of propagation filters that have proven to be superior to existing image filters in both quantitative and qualitative assessments [6].

The another paper of image fusion is “Image Fusion using NSCT Theory and Wavelet Transform for Medical Diagnosis”, authors are P. J. Anju et.al. There are different methods for medical image fusion. NSCT based fusion is further enhanced for better quality by integrating with wavelet fusion. The experimental results are tested and compared with other fusion methods by using the Peak Signal to Noise Raito (PSNR) and Structured Similarity Index Measure (SSIM) [7]. Md. Sujan et. al. (2016) proposed ” A Segmentation-based automated system for the detection of brain tumors”. In this work, we proposed threshold processing and a morphological method for detecting a tumor. Authors compared the results of the proposed method with the color segmentation method. They recognized the tumor area by comparing the true positive rate of segmented results. All results are tested with 72 flair sequences of the BRATS dataset [8]. Jyothsna et. al. (2015) proposed “Adaptive K-means clustering for Medical Image Segmentation”. A number of the group’s researchers focused on improving the clustering process. The proposed method of promoting the adaptive method is that clusters grow without first selecting the elements that constitute the cluster. It was discovered that it is capable of segmenting the region of different distribution intensity smoothly.

The method was used to achieve a significant process of accelerated research. In this paper, an adaptive clustering algorithm for K-tools is presented and does not depend on seed selection to initialize cluster K. The algorithm is tested for various images and works smoothly, resulting in good data separation and research resulting in the data structure being accelerated remarkably. One can conclude that adaptive to means that it works better, and the speed of K means [9].

Bobotov´ et al. (2016) proposed the title with “Segmentation of Brain Tumors from Magnetic Resonance Images using Adaptive Thresholding and Graph Cut Algorithm”. They got the result of comparison Graph cut result and result without Graph cut [10]. The following article is described by Edily et al. entitled with “Detection and localization of brain tumors in magnetic resonance”. The present inventors propose an automatic frame for the detection and localization of brain tumors capable of detecting and locating brain tumors in magnetic resonance images. The framework for detection and location of brain tumors proposed involves five steps: image acquisition, preprocessing, detection of edges, grouping of modified histograms and morphological manipulation. After morphological manipulation, the tumor appears as a pure white color on a pure black background. This system reached an error rate of 8%. Preliminary results demonstrate how a simple automatic learning classifier with a simple set of image-based features provides high classification accuracy. The preliminary results also demonstrate the effectiveness and efficiency of our 5-step approach to brain tumor detection and detection and extend this framework to detect other types of tumors in other types of medical images and motivate them to be localized [11].

Cabria et al. (2015) proposed “Automated Localization of Brain Tumors in MRI Using Potential-K-means Clustering Algorithm”. In this paper, they viewed the intensity of a pixel as equal to its “workload” and employed an unsupervised learning algorithm called potential-K-means that generates a balanced distribution of the pixels into clusters of approximately equal total intensity. A set of 22 images of the FLAIR MRI (axial plane) modality from the BRATS dataset was used [12]. S. Priyanka, Dr. AS Naven kumar proposed the name of the noise elimination document “Noise Removal in Remote Sensing Image Using Kalman Filter Algorithm ” in 2016. Remote sensing, in general, using sensors installed on airplanes and space platforms, the authors discussed Gaussian noise and speckle noise (salt and pepper). In this proposed study, authors reduced image noise using the Kalman filter and the Wiener filter. The Kalman filter is suitable for reducing noise while maintaining the basic structure of the image compared to other filters. The Kalman filter shows more filters with improved noise efficiency [13]. The next document is “An interactive graph cut method for brain tumor segmentation “, which is described by N. Birkbeck et al. We have developed a interactive semiautomatic brain tumor segmentation system that incorporates interactive 2D tools and automated 3D Propose Control. The method provided is based on the energy that incorporates the available MRI modalities and the regional statistics calculated in the normal normalization period. The improvement of the new parameters includes the adjustment of the continuous balance of the adhesion parameters of the operator control and the user interaction in 2D line using Rasso and the brush tool (not including the point and plot click used in the segmentation previous interactive) There is. This improves segmentation control by drastically changing the statistics of the region and limiting the segmentation. Experiments have shown that the proposed tool accelerates segmentation compared to traditional manual segmentation and reduces reproducibility between users and users [14].S. Priyanka, Dr. AS Naven kumar proposed the name of the noise elimination document “Noise Removal in Remote Sensing Image Using Kalman Filter Algorithm” in 2016. Remote sensing, in general, using sensors installed on airplanes and space platforms, the authors discussed Gaussian noise and speckle noise (salt and pepper). In this proposed study, authors reduced image noise using the Kalman filter and the Wiener filter. The Kalman filter is suitable for reducing noise while maintaining the basic structure of the image compared to other filters. The Kalman filter shows more filters with improved noise efficiency [13]. The next document is “An interactive graph cut method for brain tumor segmentation “, which is described by N. Birkbeck et al. We have developed an interactive semiautomatic brain tumor segmentation system that incorporates interactive 2D tools and automated 3D Propose Control. The method provided is based on the energy that incorporates the available MRI modalities and the regional statistics calculated in the normal normalization period. The improvement of the new parameters includes the adjustment of the continuous balance of the adhesion parameters of the operator control and the user interaction in 2D line using Rasso and the brush tool (not including the point and plot click used in the segmentation previous interactive) There is. This improves segmentation control by drastically changing the statistics of the region and limiting the segmentation. Experiments have shown that the proposed tool accelerates segmentation compared to traditional manual segmentation and reduces reproducibility between users and users [14].

3. Theory Background

3.1.  Median Filter

The median filter is a non-linear method used to eliminate noise from the MRI brain images. And it is especially effective for eradicate salt and pepper noise. The median filter works by scrolling the pixel of the image with a pixel, replacing each value with the median value of the neighboring pixels. Pixels are calculated from the first sorting of all pixel values of adjacent patterns in the order, and then replace the pixel when viewed with a half pixel value. The median filter is capable of eliminating noise without degrading the sharpness of the image [5].

        y[m,n]=median{x[i,j],(i,j)ɛω}                              (1)

Where ω is a neighborhood defined by the user, centered around location [m,n] in the image. An example of median filter of 3*3 kernel or window size is shown below. We take the original values and order the values to 0, 2, 3, 3, 4, 6, 10, 15 and 97. We find the medium value and fill this value to the center point. So, centered value 97 is replaced by the medium of all nine values 4.

Unfiltered value	Filtered value

3.2.  Wiener Filter

Anti-aliasing is the Wiener (non-linear) filter. This filter simultaneously eliminates noise and blurry integrals. There are two parts of the work: the inverse filter and the noise leveling. The Wiener filters are a class of optimal linear filters, with noisy data because the inputs are the calculation of the difference between the output sequences required of the actual output. Performance supervision can be considered the error of least squares. There is also a Wiener2 filter is an adaptive 2-D noise removal filter. This function works as a filter application. Wiener is a type of image for a linear adaptive filter that adapts to the local variance of the image. Wiener2 has done little to smooth out the great variance. At the small wiener2, more sanding is lit. Therefore, it is often better than linear filtration. In comparison, an adaptive filter is more intuitive than a comparable linear filter, parts of the profiles and high-frequency images. There is no design work, the wiener2 function processes all preliminary calculations, preliminary calculations and filter equipment and the implementation of the general input filter. The Wiener2 filter is more suitable for repairing Gaussian noise.

3.3.  Image Fusion

Image fusion is a method of integrating all images of applicable information and balanced similar sources or multiple sources in one merged image without any degradation. The main goal of merging medical imaging is the reliable integration of the observation from different input images into one image, not including any degradation and loss of visual information. There were three main ways of fusion of images – pixel level, feature level and decision level. The pixel level is a low fusion of images, the address of the pixels obtained at the output of the image sensor. Fusion of images at pixel level refers to a mixture of information and synergistic data collected from various image sources to provide an improved type of view. When the merging of images is combined at the pixel level directly into the information layer, the amount of information is greater. Almost all the image algorithms of the merged ones are designed to fall at the pixel level [6].

3.4.  Adaptive K-Mean Clustering

  Clustering is a major problem in a wide range of fields, such as pattern recognition and artificial vision. The general grouping method is based on the average K. However, it has four main drawbacks. First, it is a late and incorrect time scale. Second, it is often not desirable to wait for the user to identify the number of clusters. Third, it can exacerbate excellent areas. Finally, its performance depends to a large extent on the initial center of the cluster. To overcome the above drawbacks, the grouping algorithm 4 in this document means that K (AKM) is effectively adapted. The AKM to estimate the correct number of clusters and obtain the initial segmentation of the histogram in the center of the linear norm with the linear norm is composed of a set of data and then a local heuristic improvement to group the K means to avoid the optimal values. Execute the algorithm In addition; the kd tree is used to store data sets to accelerate. AKM has been tested on synthetic and real image data sets.

3.5.  Morphological Operation

In morphological operations, binary images and structural elements are often used as input and in combination with use of switches (intersections, conjunctions, inclusions, complements). The processed image object is based on the characteristics of the shape encoded by the input structure element. Mathematical details are described in mathematical morphology. Each pixel of the image, as well as each pixel of the whole image, is compared to a set of elementary pixels. If the group of two elements corresponds to a condition defined by a group operator (for example, when a plurality of pixels of the structural element is a subset of the pixels of the basic image), the pixels below the origin of the structural element are determined Values ​​(for binary images, prerequisites 0 or 1).

Opening. Opening eliminates small objects in the foreground (usually taken as a bright pixel) of images by placing in the background, while closing is eliminating small holes in the foreground and changing the background of small islets in the foreground. These methods can also be used to find specific paths in the image.

    AᵒB= (A ΘB) ÅB                                                      (2)

Where Θ and Å indicate erosion and dilation, respectively.

Closing. When processing images, closing together with the opening, the basic workhorse of morphological is to eliminate the noise. Opening is eliminating small items, while closing eliminates small holes.

   AᵒB= (AÅB) Θ B                                                       (3)

Where Θ and Å indicate erosion and dilation, respectively.

4. Materials and Methods

4.1.  Proposed Method

MRI images are posh by noise such as rice (Rician), Gaussian, salt and pepper. In order to confiscate noise, many noise filtering methods have been proposed. In this system, we propose a fusion method of results for improving MRI image. The way to fuse the results is built by fusion the results of the median filter with the results of the Wiener filter. Direct fusion method is used when merging results. The performance of the medium filter and the winning filter depends on the size of the core or the size of the window. We evaluate and select the best kernel in our study. We examined the choice of kernel size by testing three sets of MRI image data. They are the data set BRATS, DICOM, TCIA. The values ​​of the kernel (3, 5, 7 and 9) or the size of the window are tested and analyzed. Figure (1) shows a part of the sample image of the data set tested for kernel analysis. In MRI images, noise elimination and kernel value [3 * 3] are very effective in processing time and reconstructed image quality.

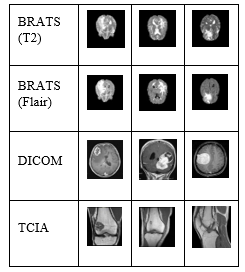Figure 1: Sample images of datasets

Table 1: Average result of kernel analysis on T2

Kernels	Median Filter		Wiener Filter
	RMSE	PSNR	RMSE	PSNR
3*3	5.506	33.499	2.677	39.646
5*5	8.946	29.221	3.91	36.35
7*7	11.368	27.107	4.966	34.265
9*9	13.175	25.810	5.905	32.757

Table 2: Average result of kernel analysis on flair

Kernels	Median Filter		Wiener Filter
	RMSE	PSNR	RMSE	PSNR
3*3	5.567	33.645	2.782	39.557
5*5	8.971	29.483	3.918	36.511
7*7	11.044	27.608	4.648	34.974
9*9	12.623	26.406	5.294	33.822

Table (1), (2), (3) and (4) present the average values of all kernels on T2, Flair, DICOM and TCIA datasets respectively. Allowing to the results of the analysis, the kernel [3 * 3] is ideal for the elimination of noise and the emphasis processing of the MRI images. Therefore, in this article, we select the median filter and the kernel value [3 * 3] of the Wiener filter.

Table 3: Average result of kernel analysis on DICOM

Kernels	Median Filter		Wiener Filter
	RMSE	PSNR	RMSE	PSNR
3*3	4.516	35.306	3.888	36.607
5*5	9.965	28.352	6.996	31.428
7*7	15.301	24.580	9.410	28.827
9*9	20.171	22.150	11.324	27.213

Table 4: Average result of kernel analysis on TCIA

Kernels	Median Filter		Wiener Filter
	RMSE	PSNR	RMSE	PSNR
3*3	8.096	31.086	5.269	34.248
5*5	5.077	34.052	4.637	34.841
7*7	6.672	31.680	5.771	32.940
9*9	7.898	30.214	6.483	31.929

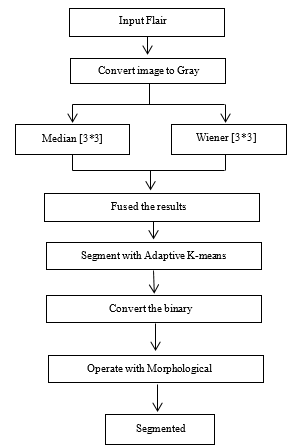Figure 2: Overview of Proposed System.

Second proposed method is the combination of Adaptive K-means clustering and Morphological operation for MRI images segmentation. The system receives the RGB image and converts the RGB image into a grayscale image. Then, the grayscale image is filtered simultaneously by the medium filter and the Wiener filter. Medium and winning filters use the kernel value [3 * 3] or the size of the window to reduce noise. [3 * 3] The value of the kernel is more powerful and adequate to eliminate noise from MRI images [15]. Therefore, this kernel is used in this research document. Both filtered results are combined with image fusion. The merged image is segmented using adaptive k-means clustering, after which the segmented image is transformed into a binary image with a threshold of 0.7. The morphological operation re-segments the binary image. In this way, the operation closing and opening are used in order. Closing is [1; 1; 1; 1; 1; 1; 1] value of the kernel and the value of the kernel value Opening is [1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]. After applying the morphological manipulation, the system generates images of the tumor segment.

5. Experiments

5.1.  Image Enhancement Results

The proposed system is constructed by fusion the result of the Medan filter and the result of the Wiener filter. The results of the proposed method are compared with the Medium filter and the Wiener filter. The results of these methods are evaluated using the values ​​of MSE (mean square error) and PSNR (peak signal noise ratio). The table (5) shows the average results of 40 images of Flair and T2. In figure (3), the design of results fusion method is described.

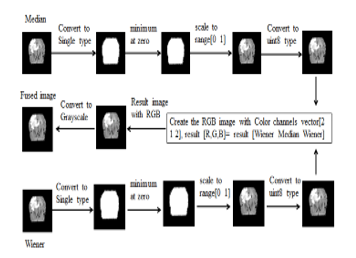Figure  3: Design of the fusion-base results binding method

Table 5: Average result of MSE and PSNR on 40 flair and 40 T2

Method	MSE		PSNR
	T2	Flair	T2	Flair
Median filter	28.6604	35.5557	34.1986	33.3925
Wiener filter	31.6925	32.9356	33.4274	33.2784
Proposed Method	21.9649	25.8498	35.1073	34.5308

Table 6: Average result of 72 flair images

Methods	TPR (%)	TNR (%)	PVP (%)	A (%)
AKM	58.47	99.34	87.21	96.16
AKMM (proposed)	85.41	98.90	78.30	98.30
Otsu	55.998	99.39	88.55	95.08
Region growing (RG)	73.64	99.28	86.50	97.42
Particle Swarm Optimization (PSO)	56.10	99.39	88.58	95.13
Interactive Graph Cut (IGC)	42.00	92.64	85.49	86.20

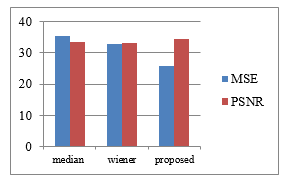Figure 4: Overview of the Results of MSE and PSNR on T2

5.2.  Image Segmentation Results

In this system, the combination of adaptive K-means clustering and morphological approach (AKMM) is proposed for tumor segmentation. Tumor segmentation was tested by two ways to detect advantages and disadvantages of proposed algorithm. First, it was tested with the algorithm which consists only of proposed results fusion method and adaptive K-means clustering (AKM) algorithm. Second, it was tested also with the morphological operation. There are two evaluation methods to use testing accuracy of tumor segmentation. First method includes True positive rate, True negative rate, Predictive value positive and Accuracy. Second method includes Jaccard Similarity index.   Resulting tumor segmentation was divided into true positive (TP), true negative (TN), false positive (FP) and false negative (FN) regions. TP represents pixels where tumor was detected and it should be tumor. TN means that tumor was not detected and should not be. FP is when tumor was detected and should not be. Finally if tumor was not detected, but should be, it is FN. Statistical methods were used to evaluate results:

True positive rate – sensitivity (TPR):

            TPR=TP/TP+FN                                                             (4)

True negative rate- specific (TNR):

            TNR=TN/TP+FN                                          (5)

Predictive value positive – precision (PVP):

            PVP=TP/TP+FP                                       (6)

Accuracy (A):

           A=TP+TN/TP+FP+TN+FN                                     (7)

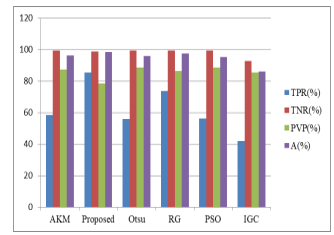Figure 5: The Results of Compartment Method.

Table 7: Average result of Jaccard similarity index in 72 flair images

Methods	Jaccard	Rfn	Rfp
AKM	0.527(min= 0.174, max=0.7996)	0.9953	1.44
AKMM (proposed)	0.6851(min= 0.3672, max=0.8427)	0.9958	1.011
Otsu	0.51(min= 0.0699, max=0.834)	0.9953	2.12
Region growing (RG)	0.647(min= 0.1124, max=0.87)	0.9954	1.594
Particle Swarm Optimization (PSO)	0.513(min= 0.0672, max=0.834)	0.9953	2.13
Interactive Graph Cut (IGC)	0.393(min= 0, max=0.840)	0.9954	2.437

Table 8: Run time duration of compartment methods

Methods	TPR (%)	TNR (%)	PVP (%)	A (%)
akmm	78.66	99.03	79.81	97.9
psom	66.16	99.29	85.99	96.47
OtsuM	66.44	99.29	85.99	96.47

Jaccard similarity coefficient is a statistic used for comparing the similarity and diversity of sample sets. rfn is ratio of false negative and rfp is ration of false positive.

Jaccard(A,B) =  êA Ç B ê/ êA È B ê              (8)

rfn = B – êA Ç B ê/ B                                        (9)

rfp = A –  êA Ç B ê/ B                                    (10)

Table 9: Performance and comparison analysis of proposed method in BRATs dataset

Performance and comparison analysis of proposed method BRATS brain tumor dataset
Algorithm	MRI modalities	Approach	True positive rate
Md. Sujan, Nashid Alam(2016)	72-Flair	Thresholding and morphological processing	84.72%
Proposed	72-Flair	Adaptive k-mean clustering and morphological processing	85.41%

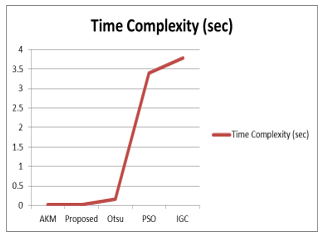Figure 6: Time Complexity of Comparement Method

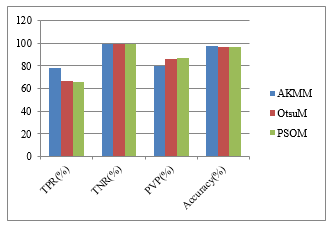Figure 7: The Averages Results of 110 Flair Images

Table 10: Average results of 110 flair images

Method	Run-time (sec)
AKM	0.0106524
AKMM (proposed)	0.0192652
Otsu	0.15238
PSO	3.39533
IGC	3.77659

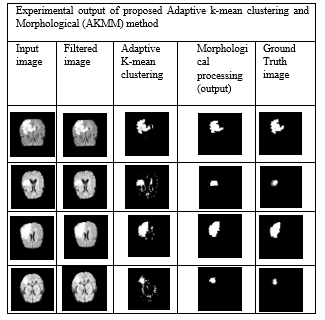Figure 8: Experimental output of proposed Adaptive k-mean clustering and Morphological (AKMM) method

      Table 10 describe about the average experimental results of 110 flair images. In this table, Our proposed method (AKMM) is compared with combination of Otsu and morphological operation and the combination of particle swarm optimization (PSO) and morphological operation. According to the results, our proposed method is more exceeding in Accuracy.

5.3.  Research Discussion

In this article, we proposed tow contributions. First is fusion –based results binding to get better result of MRI images enhancement. In this method, we fused the results of Median filter and Wiener filter. At that time, we used more Wiener effect. Thus, our enhancement method image is more smoothness than original and we also save image sharpening from Median filter properties. Among the segmentation methods, almost the segmentation based segment methods are more suitable with median filter and almost the clustering base segment methods are more suitable with wiener filter. Our filtering and enhancement method can be used in both of segmentation.  According to experimental results, our enhancement method got better results than Median filter and Wiener filter in MSE and PSNR values. So, we proposed first contribution is better results. And then, we proposed the second contribution.

Second contribution is combination of Adaptive K-means clustering and morphological operation (AKMM). We used proposed filter method in the preprocessing stage.  First paper described the results based on 72 flair images. In this article, 110 flair images are tested and described. We also used the Jaccard similarity index in experimental results evaluations. Our proposed method (AKMM) got better results than other comparative base-line methods in accuracy and run time duration. All of the base-line methods are downloaded from matlab file exchange site and re-implemented by our self.

6. Conclusion

In this work, 40 flair and T2 sequences are tested for enhancement of MRI images and 110 flair sequences are tested for tumor segmentation. The fusion based results binding method was proposed for MRI images enhancement and combination of morphological operation and adaptive K-means (AKMM) for tumor segmentation. According to our experimental results, the proposed improvement is superior to Median filter and Wiener filter. Then we test and compare base-line methods such as Otsu’s threshold, region growth, particle swarm optimization, and interactive graph cut segmentation with the proposed method (AKMM). The proposed method and all base-line methods are tested on 72 flair images and 110 flair images. The proposed method (AKMM) gained higher accuracy than the basic method compared, and it gets less complex over time.

1.  Aye Min and Zin Mar Kyu, “MRI images Enhancement and Tumor Segmentation for Brain”, 18th International Conference on Parallel and Distributed Computing, Applications and Technologies, 0-7695-6330-9/17/31.00©2017IEEE DOI 10.1109/PDCAT.2017.00051
2.  S. Jeevakala, B. Therese, “Non Local Means Filter Based Rician Noise Removal of MR Images”, International Journal of Pure and Applied Mathematics, Volume 109 No. 5 2016.
3.  M. N. Nobi and M. A. Yousuf, “A New Method to Remove Noise in Magnetic Resonance and Ultrasound Images”, Journal of Scientific Research (JSR) Publication, 2011.
4.  B. Shinde and A.R. Dani, “Noise Detection and Removal Filtering Techniques in Medical Images”, International Journal of Engineering Research and Applications (IJERA), Vol. 2, Issue 4, pp.311-316, July-August 2012.
5.  A. Mihailova, V. Georgieva, “Comparative Analysis Various Filters for Noise Reduction in MRI Abdominal Images”, International Journal “Information Technologies & Knowledge” Volume 10, Number 1, © 2016.
6.  Rick Chang, J. H., & Frank Wang, Y. C., “Propagated image filtering” In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 10-18) 2015.
7.  P. J. Anju, Dr.D.Loganathan,” Image Fusion using NSCT Theory and Wavelet Transform for Medical Diagnosis”, International Journal of Computer Science and Information Technologies (IJCSIT), Vol. 7 (3) , 2016.
8.  Md. Sujan, S.A. Noman, N. Alam, M. J. Islam,“A Segmentation based Automated System for Brain Tumor Detection”, International Journal of Computer Applications (0975 – 8887) Volume 153 – No 10, November 2016.
9.  C. Jyothsna , Dr.G.R.Udupi, “Adaptive K-means Clustering for Medical Image Segmentation”,International Journal of Technical Research and Applications e-ISSN: 2320-8163, www.ijtra.com Special Issue 31(September, 2015), PP. 15-21
10.  Z. Bobotov´, and W.S. Bene, “Segmentation of Brain Tumors from Magnetic Resonance Images using Adaptive Thresholding and Graph Cut Algorithm”, The 20th Central European Seminar on Computer Graphics, Slovakia, Proceedings of CESCG 2016.
11.  Azhari, E. E. M., Hatta, M. M., Htike, Z. Z., & Win, S. L. “Brain tumor detection and localization in magnetic resonance imaging” International Journal of Information Technology Convergence and services (IJITCS), 4(1), 2231-1939 2014.
12.  I. Cabria, I. Gondra,“Automated Localization of Brain Tumors in MRI Using Potential-K-means Clustering Algorithm”, IEEE, 12th Conference on Computer and Robot Vision 2015.
13.  S. Priyanka, Dr.A.S.N. kumar, “ Noise Removal in Remote Sensing Image Using Kalman Filter Algorithm”, International Journal of Advanced Research in Computer and Communication Engineering Vol. 5, Issue 3, March 2016.
14.  Birkbeck, N., Cobzas, D., Jagersand, M., Murtha, A., & Kesztyues, T. “An interactive graph cut method for brain tumor segmentation”. In Applications of Computer Vision (WACV), 2009 Workshop on (pp. 1-7). IEEE.
15.  Aye Min and Zin Mar Kyu, “Kernels analysis in MRI images Noise Removal Methods”, 16th International Conference on Computer Application,ICCA(2018).

(Click Here)

(Click Here)