Metaheuristics for Solving Facility Location Optimization Problem in Lagos, Nigeria

Facility location problem is a problem that many organizations still face today because of its increasing constraints and objectives. Decision makers want this problem solved in order to maximize profit and as such, it became a field of interest to many computer scientists over the years. The solution tool used by these scientists; a function of technological advancement, has evolved from the use of classical mathematical approaches to the use of metaheuristics. Some of the metaheuristics used include particle swarm optimization metaheuristics, genetic algorithm metaheuristics and tabu search. The problem considered in this research evolves the study of waste management in Lagos state. How the location of waste evacuation centers could be allocated in order to minimize resources such as transportation cost, facility cost, distance and the capacity of each centers. A mathematical model was developed that serves as a template for the algorithm used to solve the problem. Then particle swarm optimization metaheuristics was used to find the optimal solution in terms of capacity to the problem. Particle swarm optimization minimizes the use of memory and still gives a satisfactory solution. With the result obtained, respective agencies could make good decision as to the best location to build a new facility.

Full Text

1. Introduction

The study of facility location problem, also known as location analysis, is a branch of operations research and computational geometry concerned with the optimal placement of facilities to minimize resources such as cost, time, distance, etc. In most cases, the cost minimized is transportation cost. There are different areas facility location problem could be considered. These areas may include logistics facilities, warehouses, farm facilities, police stations etc. For this project, we considered a waste management facility known as evacuation centers. Waste generated from the residents at the state are dumped at the evacuation centres where it is recycled. We chose the waste management facility problem because of the way it affect our environment especially the Lagos state government. The state is very keen to the management of waste generated because of her thriving effort to becoming a green state. In this effort, the government has employed private own company known as Visionscape for the management of her waste. We have approximately 21 million people living in Lagos state and quite a large amount of waste are generated in the state daily. When the waste are not well managed based on poor allocation of the evacuation centres this could lead to air pollution of the environment. However, selecting locations out of the blues are not best measures to obtain a reasonable result. Hence, after the study of major works done on facility location, we embark on finding scientific ways of solving the problem that will give a satisfactory result. This led to the use of metaheuristics.

Metaheuristics is a higher-level procedure or heuristic designed to find, generate, or select a heuristic (partial search algorithm) that may provide a sufficiently good solution to an optimization problem, especially with incomplete or imperfect information or limited computation capacity. Examples of metaheuristics are particle swarm optimization (PSO), hill climbing, simulated annealing, tabu search, genetic algorithm, etc. Figure 1 shows the classification of metaheuristics. Different analysis have been used over the years for these classes to be obtained and presented as a clear cut direction [1].

2. Related Literature

Over the past decades, the study of facility location problem has grown even more popular, not only in the academic literature but also in practice. Facility location problems are often strategic in nature and entail long-term decisions, exposing firms to many uncertainties during the operational lifetime of a facility. When solving such problems, a firm may have to determine the number of facilities to open, their locations, and their capacities. Because

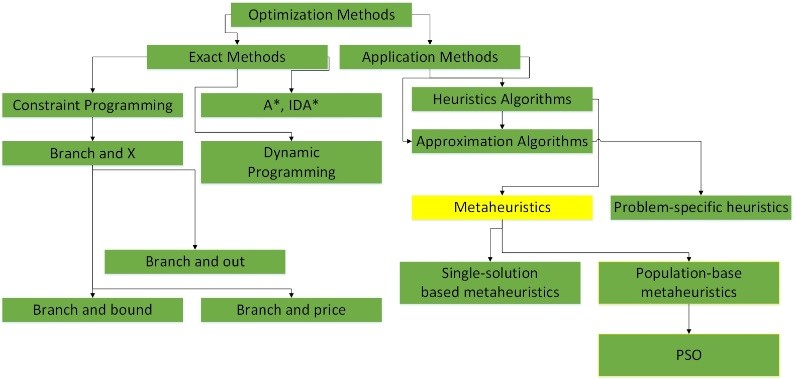Figure 1: Classification of metaheuristics.

of the high fixed costs incurred in changing a network of facilities, a firm may be limited in the frequency in which it re-examines these strategic decisions. After determining its facility network, the firm is often relegated to making operational decisions such as determining production quantities, service levels, and allocation of supply to demand. Thus, facility location problems often have a two-stage approach to solving them, location followed by evaluation. Facility location problem belongs to the class of a combinatorial optimization problem [2].

The 17th Century marks the beginning of the facility location problem which was considered as a classical mathematical problem [3]. As time went on, it became an interest to many scientists and researchers because of how it relate to real life issues. Also, various aspect of facility location problem have been considered by earlier scientist ranging from customer facility management to logistics management. [4]. However, the problems are majored on customer and warehouse facility. Also, facility location problem is further considered as capacitated [5, 6, 7] and uncapacitated [8]. Capacitated in terms of considering the size of the facility involved or the ability of the facility to manage other entities involved like customer adequately. While uncapacitated doesn’t consider the size of the facility, it assumes the facility could always manage the entities involved. Both capacitated and uncapacitated were considered by Bumb and March [9].

Mauricio and Renato presented a multistart heuristic for the uncapacitated facility location problem [10]. The method used combines elements of several other metaheuristics, such as scatter and tabu search (which make heavy use of path-relinking) and genetic algorithms (that deals with the notion of generations) to proffer solutions.

In order to have a good understanding of the various state of facility location problems, Andreas et al. [11] studied continuous location models, network location models, mixed-integer programming models, and applications of facility location problem. In [12], the author proposed particle swarm optimization, simulated annealing and iterated local search metaheuristics for solving facility location problem that has to do with the health sector. The problem was modelled and the experimental results show that the proposed algorithms reach acceptable performances in a reasonable computation time. In [13], the auhtors considered forty hospitals and three candidate municipalities in the sub-northeast region of Thailand, and considered multiple factors such as infrastructure, geological and social & environmental factors, and calculating global priority weights using the fuzzy analytical hierarchy process (FAHP). Also, a new multi-objective facility

location problem model which combines FAHP and goal programming (GP), namely the FAHP-GP model, was tested. Their proposed model led to selecting new suitable locations for infectious waste disposal by considering both total cost and final priority weight objectives. The novelty of the proposed model is the simultaneous combination of relevant factors that are difficult to interpret and cost factors which require the allocation of resources.

From the above literature, facility location problems cut across different horizon of research, and few research have provided an overview of the models and algorithms that are applied to the optimization in solving facility location problem that has to do with waste management.

3. Methodology

In this paper, we studied the problem of allocation of new evacuation centres at different potential locations such that it could manage the local government areas assigned to it in relation to the existing potential locations. The major entities are evacuation centres, potential location and local government areas. Evacuation centres are spaces where wastes are dumped and recycled. Whereas, potential locations are the positions where a facility can be allocated. Finally, the waste are generated from the local government areas in a particular city. The problem was well formulated following the principles that governs optimization model. The objective of the optimization model is to minimize the total cost of evacuation sites to be located, chosen among a set of candidate locations. Such objective ensures not only the reduction of the visual impact due to the presence of collection sites, but also the reduction of the overall cost related to the collection phase. Following below are the indices, parameters and decision variables for the model.

3.1. Definition of model components

INDICES:

= is the index of each potential location(Town) in the state, = 1,2,…m (m=3)
= is the index of each Evacuation Center, = 1,2,…n (n=2)
= is the index of each Local Government Area (LGA), = 1,2,…t (t=21)

PARAMETERS:

= is the facility cost (Naira)
= is the weight of the factor affecting a location
= is the transportation cost between the potential location and LGA(Naira)
= is the distance between the potential location and LGA(km)
= is the size of each evacuation center
= is the quantity of refuse generated by a LGA

DECISION VARIABLES:

= is a binary variable where it is 1 if the LGA is served by Potential Location and 0 if not served
= is a positive integer value where it is 1 if the Potential Location is selected and 0 if not selected
= is a binary variable where it is 1 if the Potential Location is opened by selecting Evacuation Center and 0 if otherwise

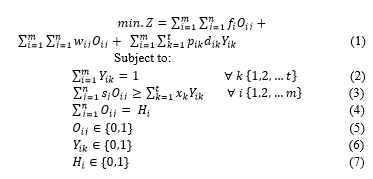Equation (1) is the objective function which is defined to minimize the total cost based on the facility cost, factors affecting the potential location and the transportation cost. Equation (2) ensures that the demand of each LGA is met. Equation (3) ensures that the sum of service by the LGA does not exceed the capacity of the Evacuation Center. Equation (4) ensures that the selected LGAs must use k-size Evacuation Centers. Constraints (5), (6) and (7) are binary decision variables. From this model, we applied particle swarm optimization technique to proffer an optimized solution on the capacity for each evacuation centers. For the PSO algorithm the following parameters below were used in relation to what was used by Jordanski:

Initial weight w = 0.9
Number of particles = 40
Cognitive constant c1 = 2
Social constant c2 = 2
Maximum velocity vmax = capacity_range[0]
Minimum velocity vmin = capacity_range[1]

Pseudocode 1: To find the optimal location for the evacuation centers

Initialize Parameters, Decision Variables and Indices
For (All number of Locations) {

For (All number of LGA) {

ObjCost FacilityCost + WeightCost + TransportationCost

}

ObjCostRow [ ] ObjCost

}
MinObjCost sort(ObjCostRow)
MinCapacity Pso(Capacity)
Return MinObjCost, MinCapacity

Pseudocode 1 shows the steps involved to solve the facility location problem for the evacuation center. All the parameters, decision variables and indices where initialized. An iteration was done to get the mapping for the potential location to their respective local government area (LGA). This will enable us generate the network analysis for the problem and find the minimum mapping that will guarantee a minimum cost based on all the criteria considered. The single cost for each mapping are placed in an array called ObjCostRow as shown above. It is sorted in an ascending order and pass to MinObjCost. The capacity generated for each evacuation center is passed to the PSO function which returns the minimal capacity for evacuation centers. Lastly, the result are displayed.

4. Application of the proposed methodology

The method was implemented with the PHP programming language and designed with web technologies such as HTML and CSS to make it easy for users to interact with. All the user needs to do is to supply the required parameters needed in the right form and the system validates the parameters provided and process it. Finally, the result is displayed to the user.

Figure 2: User interface for the parameters.

Potential Location: This field requires the user to enter the number of potential location in consideration. The potential location is the location where the user desire to locate the facility. The value must be an integer.
Evacuation Centre: This field requires the user to enter the number of evacuation center required to be allocated at the potential location. The value must be an integer.
LGA: This field requires the user to enter the Local Government Area in the state where the refuse are coming that are to be managed by the evacuation center. The value must be an integer.
Facility Cost: This field requires the user to enter the cost of building as the case may be at a particular potential location. The values are separated by a comma. The values must be a set of numbers and must correspond to the number of potential location set.
Weight Cost: This field requires the user to enter the cost of the weight generated for each potential location. The weight is generated by considering the factors affecting each potential location. This factors may include geographical factor, closeness to raw materials, electricity, good roads, etc. The values are separated by a comma. Also, the values must correspond to the number of potential location set.
Capacity Range: This field requires the user to enter the capacity search space for the problem. The capacity that is required to be managed for each evacuation center. This allows the user to know the required capacity to be considered for building a particular facility.
Quantity: This field requires the user to enter the amount of waste in kilograms (Kg) generated by a particular LGA per day/month/year. The values could be a set of real numbers and separated by commas.
Distance: This field requires the user to enter the distance from a particular LGA to a potential location in miles. The distance of the set of LGA is separated by commas and separated by a forward slash with respect to a particular potential location.
Transportation Cost: This field requires the user to enter the transportation cost for each LGA to a particular potential location. The set of transportation cost are separated by commas and separated by a forward slash with respect to a particular potential.

We carried out 3 different experiment base on the number of potential locations, evacuation centers and local government areas. We shall be considering the operation of experiment one and give a summary of the three experiment.

Table 1: Parameters for Experiment 1

m	n	t
3	2	21	10,20,30	50,70,40	20,0
	4,3,4,5,2,3,3,4,6,5,6,3,4,5,2,3,3,4,6,5,6
	2,1,2,3,4,5,6,6,8,8,9,9,1,2,1,2,3,3,3,3,2/ 3,2,3,4,5,1,2,2,9,2,2,3,4,5,2,3,3,4,6,5,6/ 4,3,4,5,2,3,3,4,6,5,6,3,4,5,2,3,3,4,6,5,6
	2,1,2,3,4,5,6,6,8,8,9,9,1,2,1,2,3,3,3,3,2/ 3,2,3,4,5,1,2,2,9,2,2,3,4,5,2,3,3,4,6,5,6/ 4,3,4,5,2,3,3,4,6,5,6,3,4,5,2,3,3,4,6,5,6

Table 1 shows that we have 3 potential locations but we want to build only 2 evacuation centers that will minimize general cost (facility cost, transportation cost, and weight cost). Using the arbitrary parameters from Table 1, the objective function was generated following the operations described in Pseudocode 1 is shown in Figure 3.

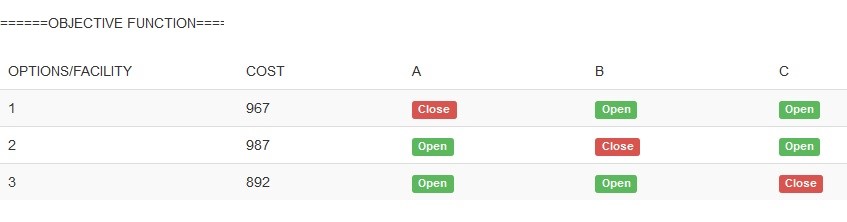Figure 3: Objective function result for experiment one.

From the objective function shown in Figure 3, we would see that the minimum cost is given by option 3. This option means the best selection would be facility A and B. The network analysis that gives this cost is shown in Figure 4. Hence, facility A would serve LGA (1,2,3,4,5,9, 13,14,15,16,17,18,19,20,21) while facility B serve LGA (6,7,8,10, 11,12).

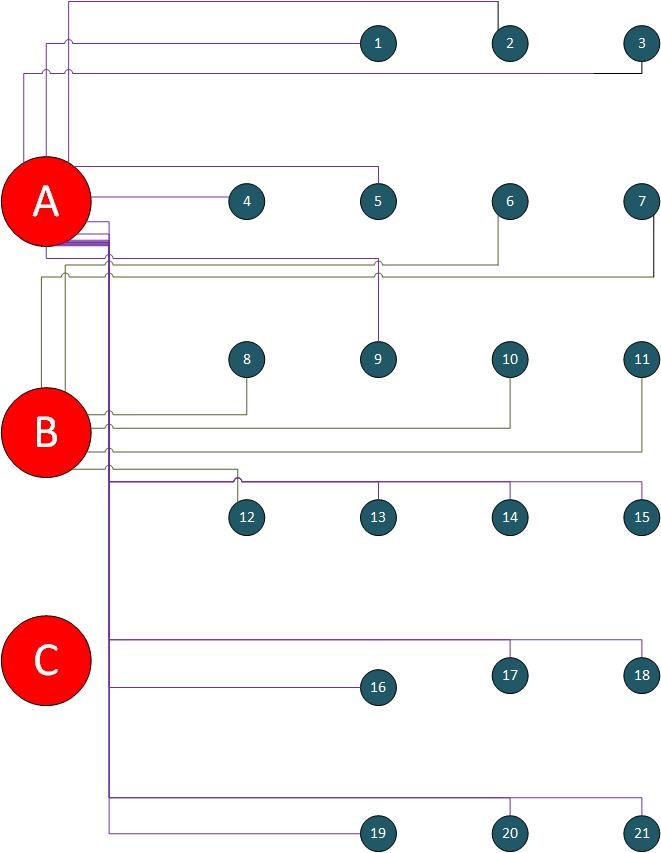Figure 4: Network analysis for experiment one.

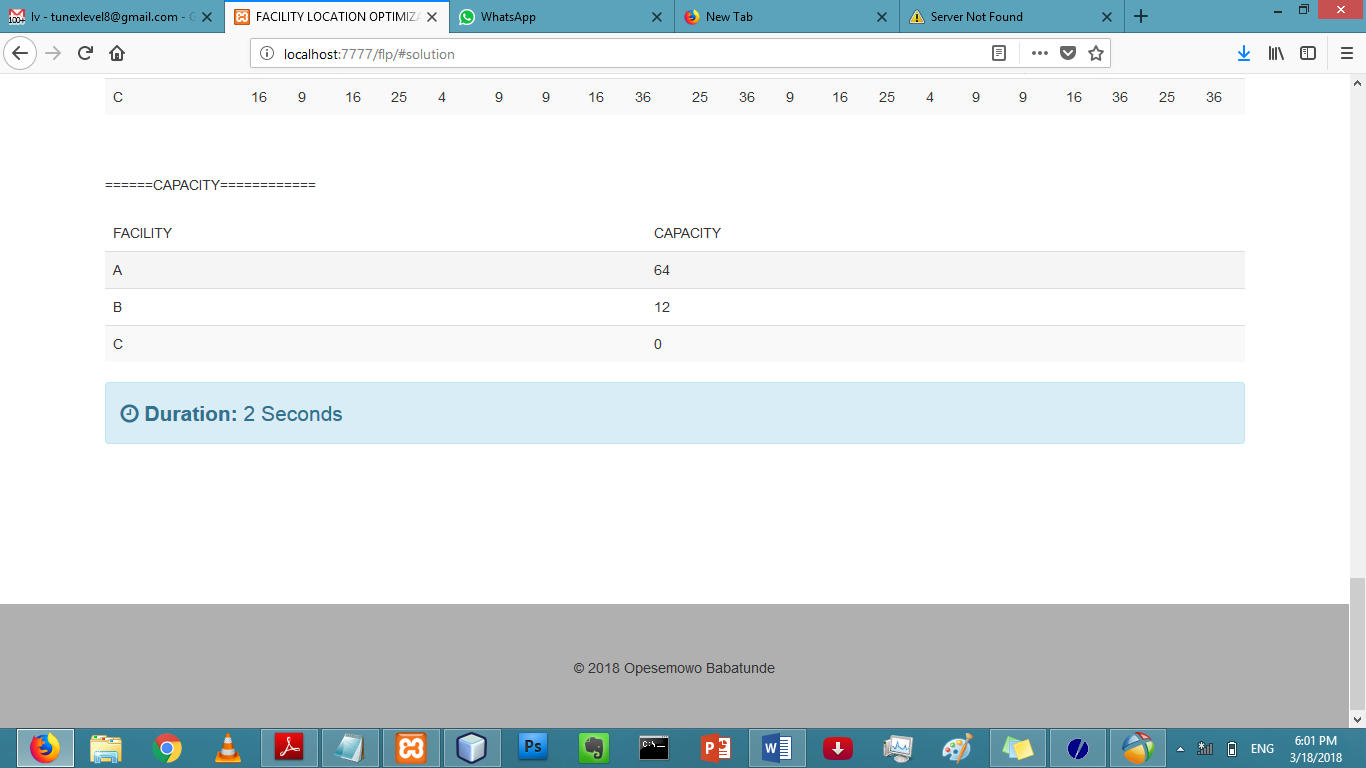Figure 5: Capacity for experiment one.

Figure 5 shows the capacity for the facilities. That is, the minimum quantity a facility should manage. The same process as explained in Section 4 was carried out for two different scenarios with respect to the potential location, evacuation center and LGA. The time duration was recorded to evaluate the scalabity of the solution in relation with time as shown in Figure 6 and 7.

Figure 6: Summary of the experiments.

From Figure 7, we could discover that the time duration compare to the other parameters is significantly small.

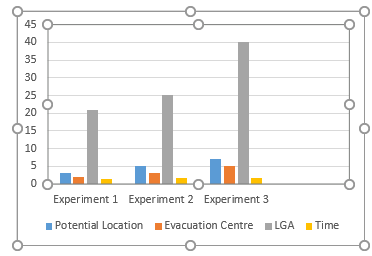Figure 7: Graphical representation of the experiments.

5. Conclusion

In this project, facility location problem was considered in regards to optimization. The waste management facility serve as the underlying problem dealt with among several problems related to the facility location problem. This problem was chosen because of it adverse effect in the economy of Nigeria especially Lagos state. A redefined PSO was proposed in solving the problem which involves finding the best location to build a set of evacuations canters that would manage the waste gotten from several local government. As most common with facility location problem, the mathematical model to the problem was given which includes the objective functions and the set of constrains involved. Then a set of instances was used to test the model. The experimental result was gotten that shows the optimal solution to the problem. Hence, we have been able to develop a model that can be used to solve the facility location problem and proffer an optimized solution to the waste management facility location problem. The application developed can also accept other values which requires solution relating to the model worked on making it a flexible solution. Further research should be carried out in other problem areas like the police station facility location, farm facility allocation and any of those that could help in building the nation. Metaheuristics are very good tool in regards to problems that tends to be complex and are unable to be solve within a limited amount of time. However, they might not guarantee optimal solution in some cases. Hence, they must be applied carefully to solve a particular problem.

References (13)

E. G. Talbi, Metaheuristics – From Design to Implementation (John Wiley & Sons, New Jersey, 2009)
S. Arifin. Location allocation problem using genetic algorithm and simulated annealing. A case study based on school in Enschede (Doctoral dissertation, Master’s thesis, the University of Twente, Enschede, the Netherlands, 92p) (2011)
R. Guner and S. Mehmet. A Discrete Particle Swarm Optimization Algorithm for Uncapacitated Facility Location Problem. Journal of Artificial Evolution and Applications, (2008).
R.H Ballau, Facility Location Decisions. In Business Logistics: Supply Chain Management (2004) 550-617
Ling-YunWua, Xiang-Sun Zhang, Ju-Liang Zhang. Capacitated facility location problem with general setup cost. Computers & Operations Research, (2006).
H. Pirkul and V. Jayaraman. A Multi-Commodity, Multii-Plant, Capacitated Facility Location Problem: Formulation and Efficient Heuristic Solution. Elsevier Science Ltd, (1997).
Y. Ren. Metaheuristics for multiobjective capacitated location allocation on logistics networks (Doctoral dissertation, Concordia University, 2011).
R. L. Francis, L. F. McGinnis and J. A. White, Facility Layout and location: an analytical approach (Pearson College Division, 1992).
A. Bumb and W. K. March. A simple dual ascent algorithm for the multilevel facility location problem: Approximation, Randomization, and Combinatorial Optimization. University of Twente (2001) 55-63
G. R. Mauricio and F. W. Renato. A hybrid multistart heuristic for the uncapacitated facility location problem. European Journal of Operational Research, (2005).
A. Klose and A. Drexl. Facility location models for distribution system design. European Journal of Operational Research, 162 (2005) 4-29.
M. Jordanski. Metaheuristic Approaches for Solving Facility Location and Scale Decision Problem with Customer Preference. IPSI Bgd Internet Research Society, 13 (2017).
N. Wichapa, P. Khokhajaikiat. Solving multi-objective facility location problem using the fuzzy analytical hierarchy process and goal programming: a case study on infectious waste disposal centers. Elsevier Science Ltd, (2017).

Metaheuristics for Solving Facility Location Optimization Problem in Lagos, Nigeria