1. Introduction

Combinatorial optimization is a topic that consists of finding an optimal solution from a finite set of solutions. Combinatorial optimization problems are often NP hard. It is often time consuming and very complex for Central Processing Unit (CPU) to solve combinatorial optimization problems, especially when the problem is very large. Metaheuristic methods can help finding optimal solution within a reasonable time.

Nowadays efficient parallel metaheuristic methods have become an interesting and considerable topic. Local search metaheuristics (LSMs) are single solution-based approaches, as well as one of the most widely researched metaheuristics with various types such as simulated annealing (SA), hill climbing, iterated local search, tabu search, and genetic algorithm etc. A common feature that local search metaheuristics can share is, a neighborhood solution is selected iteratively as a candidate solution. We can use local search metaheuristics to solve combinatorial optimization problems such as graph bisection problem, Travelling Salesman Problem (TSP) etc. Many works have been done by using parallel computing technology to improve its performance from iteration level, algorithmic level and solution level. Therefore, parallelism is a good technique for improving the solution quality as well as reducing the time complexity.

Recently, Graphics Processing Units (GPUs) have been developed gradually to parallel/programmable processors from fixed function rendering devices. GPUs motivated by high definition 3D graphics from real time market demand have become many core processors, multithreaded, highly parallel with high bandwidth memory and tremendous computational power. So, more transistors are devoted to design GPU architecture in order to do more data processing than data caching/flow control. With the fast development of general purpose Graphics Processing Unit (GPGPU), some companies have promoted GPU programming frameworks such as OpenCL (Open Computing Language), CUDA (Compute Unified Device Architecture), and direct Compute. GPU based metaheuristics have become much more computational efficient compared to CPU based metaheuristics. Furthermore, making local search algorithms optimized on GPU is an important problem for the maximum efficiency.

In the recent years, GPU computing has emerged as a very  important challenge in the research areas for parallel computing. GPU computing is believed as an extremely useful technology for speeding up so many complex algorithms in order to improve solution quality. However, rethinking of existing parallel models as well as programming paradigms for allowing their deployment on GPU accelerators is one of the major challenges for metaheuristics. In fact the issue is, revisiting the parallel models as well as programming paradigms for efficiently considering the GPUs characteristics. However, some issues related to memory hierarchical management of GPU architecture need to be considered.

The contribution of this research is, to design a GPU framework which can efficiently deal with the following important challenges while parallelizing metaheuristics methods to solve large optimization problems:

1. Distribution of data processing between GPU and CPU with efficient CPU-GPU cooperation.
2. Thread synchronization and efficient parallelism control.
3. Data transfer optimization among various memories and memory capacity constraints with efficient memory management.

Our proposed parallel models on GPU architecture can be very useful and efficient in finding better optimized solution for large scale combinatorial optimization problems. We have made a series of experiments with our proposed GPU framework to parallelize some heuristic methods such as simulated annealing, hill climbing, genetic algorithm etc. for solving combinatorial optimization problems like Graph Bisection problem and Travelling Salesman Problem (TSP). All of our experimental evaluation shows that parallelizing heuristics methods with our GPU framework provides higher quality solutions in a reasonable computational time.

2. Background

As we contribute to the parallelization of heuristics methods for combinatorial optimization problems with GPU, below we discuss about combinatorial optimization problems, some optimization heuristics methods (hill climbing and simulated annealing), graph bisection problem/ travelling salesman problem as example optimization problems and GPU architecture/ computing.

2.1    Significance of Combinatorial Optimization

Combinatorial optimization can be defined as a mathematical discipline with the interplay between computer science and mathematics [1]. Very roughly, it deals with the problem of making optimal choices in huge discrete sets of alternatives. Combinatorial optimization is a way to search through a large number of possible solutions for finding the best solution from them. When the number of possible solutions is really too large and it is impractical to search through them, we can apply different techniques to narrow down the set and speed up the search.

Many combinatorial optimization problems are known as NP hard. That means, the time needed for solving a problem instance to optimality grows exponentially with the size of the problem in the worst case. Hence, these problems are easy to understand and describe, but very hard to solve. Even it is practically impossible  to determine all possibilities for problems of moderate size in order to identify the optimum. Therefore, heuristic approaches are considered as the reasonable way to solve hard combinatorial optimization problems. Hence, the abilities of researchers to construct and parameterize heuristic algorithms strongly impact algorithmic performance in terms of computation times and solution quality.

2.2    Combinatorial Optimization Heuristics

To deal with combinatorial optimization problems, the goal is to finding such an optimal/optimized solution, which can minimize the given cost function. The cost of the algorithms can exponentially increase while the complexity of the search space is growing up,  and this can make the search of a solution not feasible.

Finding a suboptimal solution within a reasonable time is another way to address these problems. In some cases, We might even find the optimal solution in some cases. These techniques can be divided into two main groups: heuristics and metaheuristics.

A heuristic is an algorithm that tries to find optimized solutions to complex combinatorial problems, but there is no guarantee for its success. Most of the heuristics are based on human perceptions, understanding the problem characteristics and experiments, but they are not based on fixed mathematical analysis. The heuristic value should be based on comparisons  of performance among the competing heuristics. The most important metrics  for performance are quality of a solution, as well as the running time. The implementation of heuristic algorithms is easy and they can find better solutions with relatively small computational effort. However, a heuristic algorithm can rarely find the best solution for large problems.

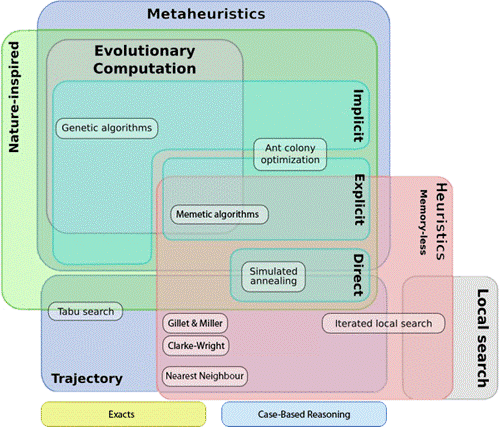Figure 1: Different classifications of metaheuristics

Over the last couple of  decades many researchers have been studying optimization heuristics for solving many real life NP hard problems, and some of the common problem solving techniques/methods underlying these heuristics came up as meta heuristics. A meta heuristic can be defined as a pattern or the major idea for a class of heuristics. Reusable knowledge in heuristic design can be represented by Meta-heuristics, which can provide us with important starting points in designing effective new heuristics for solving new NP hard problems.

Meta heuristics are not algorithms, nor based on theory. To effectively solve a meta heuristic based problem, we must have better understanding of the problem characteristics, and creatively designing as well as implementing the major meta heuristic components. So, it has become an action of research to use a meta heuristic for proposing an effective heuristic to solve an NP hard problem.

Another classification dimension is population based searches (P-Metaheuristics) vs single solution (S-Metaheuristics). P-Metaheuristics approaches maintain/ improve multiple candidate solutions, often using population characteristics to guide the search. P-Metaheuristics include genetic algorithms, evolutionary computation, and particle swarm optimization. S-Metaheuristics approaches  focus on modifying/improving a single candidate solution. S-Metaheuristics include iterated local search, simulated annealing, hill climbing, variable neighborhood search etc. Below are some of the heuristics methods to solve combinatorial optimization problems:

2.2.1 Hill Climbing

Hill climbing is a mathematical optimization technique that belongs to the local search family and can be used for solving combinatorial optimization problems. The best use of this technique is in problems with “the property that the state description itself contains all the information needed for a solution”. Hill climbing algorithm is memory efficient, since it does not maintain any search tree. This algorithm mainly looks into the present state and the immediate future states only. By using an evaluation function, it tries to improve the current state iteratively.

Hill climbing can encounter a problem called “local maxima”. When the algorithm stops making progress towards an optimal solution, local maxima problem can occur because of the lack of immediate improvement in adjacent states. There are variety of methods to avoid Local maxima. Repeated explorations of the problem space could be one of the methods for solving this problem.

Hill Climbing Algorithm:

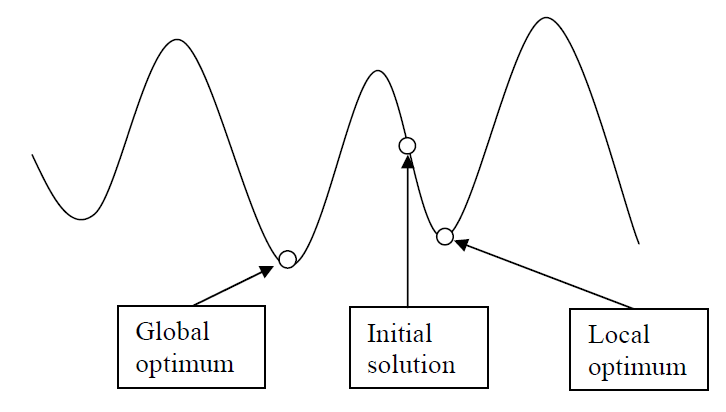Figure 2: global solutions vs local solutions.

This algorithm starts from a random initial solution and then it keeps looking in the solution space in order to migrate to better neighbor solution. We might need to compare the current partition with all the neighbor’s solutions before the algorithm is terminated. The algorithm terminates when all the neighbors’ solutions are worse compared with the current partition. This technique can only find the local optimum solutions which are better solutions than all the neighbors, but the found solutions might not be global optimum solutions. The figure 2 shows difference between global and local solutions.

It is a time consuming process to maintain the visited neighbors of the current partition. That is why, it is necessary to parallelize the hill climbing algorithm for finding the best optimized solution.

2.2.2  Simulated Annealing

For graph bisection, simulated annealing heuristic starts with a high temperature t and a randomly selected initial partition as its current partition. After that, this heuristic starts the iterations with the same temperature and at each iteration, a neighbor partition is randomly generated. If the cost of the neighbor partition is better than the current cost, then the neighbor partition becomes the new current partition for the next iteration. If the neighbor partition does worsen the current cost, it can still be accepted with a probability as the new current partition. In case of high temperature, the probability is not sensitive to bad neighbor partition. But in case of low temperature, the probability for accepting a worsening neighbor will diminish with the extent of the worsening. The temperature is reduced by a very small amount after certain iterations are completed with the same temperature, and then, the iterations continue with the reduced temperature. The iteration process terminates once the termination criteria is met.

Many combinatorial optimization problems can be solved by applying simulated annealing heuristic. Unlike other meta heuristics, it has been mathematically proven that simulated annealing converges to the global optimum with sufficiently slow reduction of the temperature. As very few real world problems can afford such excessive execution time, this theoretical result does not interest much the practitioners. Below is the pseudocode for simulated annealing heuristic.

The simulated annealing and local optimization differ with the characteristics whether worsening neighbors will be accepted. Simulated annealing heuristic starts with random walk in the solution space. If a random neighbor is better than the current solution, simulated annealing always accepts it. But, when the random neighbor is worse, the chance of accepting the worsen neighbor is slowly reduced. Simulated annealing can be reduced to local optimization with a very low temperature.

Figure 3: Simulated Annealing Algorithm

2.3    Optimization Problems

• Graph Bisection Problem

The graph bisection  problem can be defined as a data representation of a graph G = (V,E) with  a number of vertices=V  and a number of edges=E, such that the graph G can be partitioned into smaller sections with some particular properties. For example, a k-way partition can divide the vertices into k smaller sections. When the number of edges between the separated components is relatively very small, it can be defined as a good partition. We can call a graph partitioning as uniform graph partition which divides the graph into smaller components in such a way that all the components are almost the same size as well as there are only small number of connections between the components. The important applications for graph partitioning include, but not limited to  partitioning different stages for VLSI circuit design, scientific computing, clustering, task scheduling for multi-processing systems, and cliques detection in social networking etc.

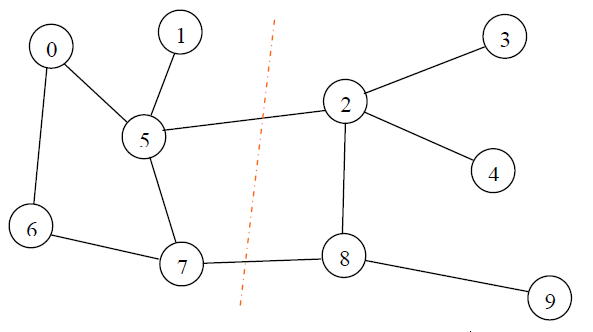Figure 4: An optimal graph bisection

• Travelling Salesman Problem

The Travelling Salesman Problem (TSP) is a combinatorial optimization problems which can be described easily, but it is very difficult to solve. A salesman starts with one city and will be visiting a number of cities with the condition that the salesman must visit each and every city only once and finally returns to first city. Selecting the sequence of the cities to be visited is the problem, because the salesman has to take the shortest path from a set of possible paths to minimize the path length. Exhaustive search can be used to find an optimal solution for a small instances (a few cities only) of TSP. But the problem is really critical for large number of cities, since with the increase in the number of cities, the number of possible paths increases exponentially. The number of possible paths for visiting n number of cities is the permutation of n which is n!. If the number of cities is increased by 1 only, the number of possible paths will become (n+1)!. Therefore, it will take too much time to compute the cost for all possible paths and find out the shortest path from them. TSP in known as a typical NP-hard problem.

TSP has a lot of applications in real world in different areas, like electronic maps, computer networking, Mailman’s job, VLSI layout, traffic induction, electrical wiring, etc.

TSP Algorithms:

2.4. GPU Architecture/Computing

Just a while ago, the conventional single core or multicore CPU processor was the only viable choice for parallel programming. Usually some of them were either loosely arranged as multicomputer in which the communication among them were done indirectly because of the isolated memory spaces, or tightly arranged as multiprocessors that shares a single memory space. CPU has a large cache as well as an important control unit, but it doesn’t have many arithmetic logic units. CPU can manage different tasks in parallel which requires a lot of data, but data are stored in a cache for accelerating its accesses. Nowadays most of the personal computers have GPUs which offer a multithreaded, highly parallel and many core environments, and can potentially reduce the computational time. The performance of the modern GPU architecture is wonderful in regards to cost, power consumption, and occupied space.

Figure 5: GPU architecture.

Figure 6: GPU thread blocks

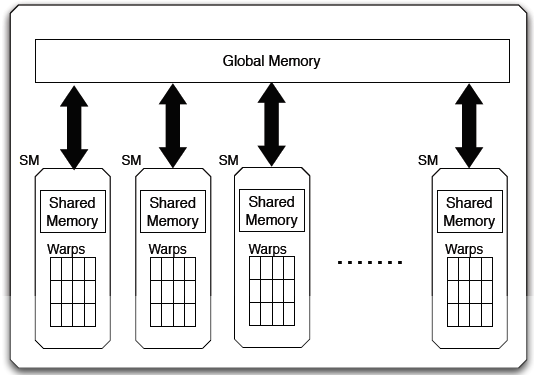
A GPU includes a number of Streaming Multiprocessors (SMs). Each streaming multiprocessor contains a number of processing units which can execute thousands of operations concurrently. The warps inside a SM consist of a group of threads. A warp can execute 32 threads in a Single Instruction Multiple Data (SIMD) manner, which means all the threads in a warp can execute same operation on different data points. GPUs have at least two kinds of memory: global memory and shared memory. Global memory allows to store a large amount of data (such as 8GB), whereas shared memory can usually store only few Kilobytes per SM.

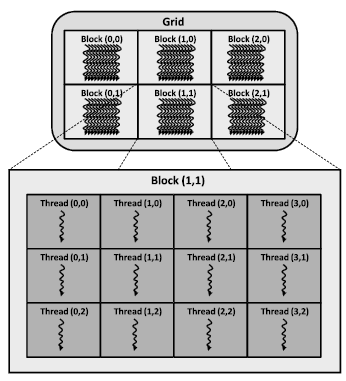
A GPU thread can be considered as a data element to be processed. GPU threads are very lightweight in comparison with CPU threads. So, it is not a costly operation when two threads change the context among each other. GPU threads are organized in blocks. Equally threaded multiple blocks execute a kernel. Each thread is assigned a unique id. The advantage for grouping of threaded blocks is that simultaneously processed blocks are linked closely to hardware resources. The threads within the same block are assigned to a single multiprocessor as a group. So, different multiprocessors are assigned to different threaded blocks. Therefore, controlling the threads parallelism can be a big issue for meeting memory constraints. As multiprocessors are mainly organized based on the Single Program Multiple Data (SPMD) model, the threads can access to different memory areas as well as can share the same code.

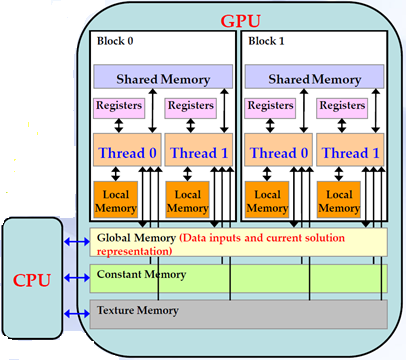Figure 7: CPU – GPU communications.

GPU is used as a device coprocessor and CPU is used as a host. Each GPU has its own processing elements and memory which are separate from the host computer. Data is transferred between the host memory and the GPU memory during the execution of programs. Each device processor on GPU supports SPMD model, which means same program can simultaneously be executed on different data by multiple autonomous processors. To achieve this, we can define kernel concept. The kernel is basically a method or function which is executed by several processors simultaneously on the specified device in parallel and callable from the host as well. The Communications between CPU host and the device coprocessors are accomplished via the global memory.

3. Literature Review

In [2, 3, 4], the author proposed GPU based works with genetic algorithms. They proposed that the population evaluation as well as a specific mutation operator are to be performed in GPU. They implemented the selection and replacement operators in CPU. So, huge data transfers are performed between GPU and CPU. This kind of techniques can limit the performance of the solution.

In [5], the author proposed evolution strategy algorithm for solving continuous problems. According to his suggestions, multiple kernels can be designed for some of the evolutionary operators like selection, evaluation, crossover, mutation etc. and CPU can handle the rest of the search process.  Later on, in [6], the author presented similar implementation with genetic algorithms. The additional contribution of their work was investigating the effect of problem size/ thread size /population size on GPU implementation comparing with sequential genetic algorithm.

In [7], the author proposed a memory management concept for an optimization problem. They implemented the concept for quadratic assignment problem where the global memory accesses were coalesced, the shared memory was used for storing as many individuals as possible, and the constant memory associated with matrices. For dealing with data transfers, their approach was a full parallelization based search process. In this regards, they divided the global genetic algorithm into multiple individual genetic algorithms, such that a thread block is represented by each sub population. Because of the poor management of data structures, the speed-ups obtained in their solution for combinatorial problems are not convincing.

In [8], the author proposed a framework of the automatic parallelization with GPU for the evaluation function. Only the evaluation function code need to be specified in their approach and the users don’t need to know CUDA keywords. This approach allows evaluating the population on GPU in a transparent way. But, this strategy has some problems, such as it lacks flexibility because of transferring the data and nonoptimized memory accesses. In addition, the solution is limited to the problems where no data structure is required.

In [9], the author proposed an implementation of an evolutionary algorithm which is a GPU based full parallelization of the search process. Without any problem structures they implemented this approach to make an application for continuous and discrete problems. Later on, the authors also submitted an implementation of their algorithm with multi GPUs [10]. However, since there are some challenging issues of the context management such as global memories of two separate GPU, their implementation with multiple GPUs does not really provide with any significant performance advantages.

In [11], the author implemented a model for continuous optimization problems in which is very similar to the previous model. In this model, shared memory is used to store each sub population and organized based on ring topology. Although the speed-ups for the obtained solution are better compared with a sequential algorithm, the implementation of this model was dedicated to few continuous optimization problems only. As by considering the two previous models no general methods were outlined, in [12], the author made some investigation on the parallel island model on GPU. By involving different memory managements, they designed three parallelization strategies and were able to address some issues.

In [13], the author proposed a multi start tabu search algorithm and implemented to the TSP as well as the flow shop scheduling problem. The parallelization is performed on GPU by using shared libraries, and one tabu search associated with each thread process. However, this approach requires so many local search algorithms for covering the memory access latency and so, this type of parallelization is not much effective. In [14], the author proposed similar approach with CUDA. In this approach, the memory management for optimization structure is done in the global memory and they implemented this to the quadratic assignment problem. However, as one local search associated with each thread, the solution performance is limited to the size of instance.

For designing of multi-start algorithms, in [15], the author provided general methodology which are applicable to local search methods like simulated annealing, hill climbing, or tabu search. They also have contribution regarding the relationship between available memories and data mostly used for the algorithms. But, the application of the GPU accelerated multistate model is very limited, because it requires so many local search algorithms at run time to become effective. In [16], the author proposed a GPU based hybrid genetic algorithm. In their approach, they implemented an island model where a cellular genetic algorithm is represented by each population. Also, the mutation step in their hybrid genetic algorithm is followed by hill climbing algorithm. They performed their implementation for the maximum satisfiability problem.

According to the previous work, the hill climbing need to be integrated with the island model as per the investigation of the full parallelization. In this regard, in [17] the author proposed the redesign of GPU based hybrid evolutionary algorithms which performs a hybridization with a local search. Their focus was on different neighborhoods generation on GPU, correlating to each individual to be mutated in the evolutionary process. This kind of mechanism may guarantee more flexibility.

In [18], the author introduced a GPU accelerated multi objective evolutionary algorithm. In his approach, he implemented some of the multi objective algorithms on GPU, but not with the selection of non-dominated solutions. There are more works on P-metaheuristics for GPU parallelization are proposed. The parallelization strategies used for these implementations are similar to the prior techniques mentioned above. These works include particle swarm optimization [19, 20, 21], genetic programming [22, 23, 24, 25] and other evolutionary computation techniques [26, 27, 28].

3.1. Research issues and contributions

Most of the approaches in the literature are mainly based on either iteration level or algorithmic level. In other words, the approaches are based on basically either the simultaneous execution of cooperative/independent algorithms, or GPU accelerated parallel evaluation of solutions. Regarding the cooperation between CPU and GPU, there are some implementations which also consider the GPU parallelization of other treatments such as selection/variation operators for evolutionary algorithms. We may argue on the validity of these choices, since an execution profiling may show that such treatments are negligible compared to the evaluation of solutions. As mentioned above, for reducing the data transfer between GPU and CPU, a full GPU parallelization of metaheuristics may also be performed. The original semantics of the metaheuristic are altered in this case to fit the GPU execution model.

Regarding the control of parallelism, a single thread with one solution are associated in most of the implementations. Besides, some of the cooperative algorithms associate one threads block with one sub population and may take advantage of the threads model. However, so far we’ve not found any work that has been investigated for managing parallelism of the threads efficiently to meet the memory constraints. The previous implementations may not be robust while dealing with large problem instances or a large set of solutions. In Chapter 4, we will show how an efficient control of thread may allow introducing fault tolerance mechanism for GPU applications.

For the memory management, so far there is no explicit efforts made in most of the implementations for memory access optimizations. For example, one of the most important elements for speeding up is memory coalescing, and additionally, could consider local memories for reducing non coalesced accesses. However, some of the authors proposed the simple way of using the shared memory to cache, but there is no performance improvement guarantee in those approaches. Some other authors also put some explicit efforts for handling optimization structures with the different memories, but still there is no general guideline/outline from those works. In fact, a lot of time, the associations of memory strictly depend on the target optimization problem such as small problem instances and/or no data inputs.

The contribution of this research is: to design a GPU framework with a set of efficient algorithms which can efficiently address the above mentioned challenges by parallelizing major metaheuristics for combinatorial optimization problems on the CPU-GPU architecture and also, to validate the solution quality with graph bisection problem as well as Travelling Salesman Problem (TSP).

4. Proposed Method and Contribution

Below are the research methodologies that we followed for proposing our methods and adding contributions to our GPU framework.

• Studying data processing distribution between CPU and GPU, and finding the challenges for efficient CPU-GPU cooperation.
• Studying thread synchronization, parallelism control on GPU threads, and finding the challenges for efficient parallelism control.
• Designing algorithms to optimizing data transfer between various memories and memory capacity constraints with efficient memory management.
• Developing parallel combinatorial optimization algorithms/frameworks for the CPU-GPU architecture to efficiently deal with the above mentioned GPU challenges.
• Validating the solution quality and efficiency of the proposed frameworks/algorithms relative to those of the best sequential meta-heuristics with extensive experimental design for graph bisection problem and TSP.

4.1. Difficulties in parallelizing optimization heuristics on GPU

Most of the time the performance of a parallel algorithm may depend on how well the communication structure of the target parallel system is matched with the communication structure of the algorithm. Nowadays one class of parallel processing systems consists of a number of processors, each with its own private memory. In addition, each of these processor memory pairs are connected to a small number of other pairs in a fixed topology. In these systems, if two processor-memory pairs must share data, a message is constructed and sent through the interconnection network. Such a message must be forwarded through one or more intermediate processors in the network. This forwarding introduces delay and hence reduces the amount of speedup achieved.

In science and industry, local search methods are heuristic methods for solving very large optimization problems. Even though these iterative methods can reduce the computational time significantly, the iterative process can still be costly when dealing with very large problem instances. Although local search algorithms can also reduce the computational complexity for the search process, still it is very time consuming for CPU in case of objective function calculations, especially when the search space size is too large. Therefore, instead of traditional CPUs the GPUs can be used to find efficient alternative solutions for calculations.

It is not straightforward to parallelize combinatorial optimization heuristics on GPU. It requires a lot of efforts at both design level and implementation level. We need to achieve few scientific challenges which are mostly related to the hierarchical memory management. The major challenges are: the CPU-GPU data processing with efficient distribution, synchronization of different threads, the data transfer optimization between different memories and their capacity constraints. Such challenges must be considered in redesigning of parallel metaheuristic models on GPU-CPU architectures for solving large optimization problems.

The following major challenges are identified for designing parallel combinatorial optimization algorithms efficiently on CPU-GPU architecture:

1. CPU-GPU Cooperation: It is important to optimize the data transfer between GPU and CPU to achieve the best performance. For efficient CPU-GPU cooperation, reparation of task must be defined in metaheuristics.
2. Parallelism control on GPU threads: In order to satisfy the memory constraints, it is important to apply the control of threads efficiently, since the order of the threads’ execution is unknown for parallel multithreading in GPU computing. Also, it is important to define the mapping efficiently between each of the candidate solutions and a single GPU thread which is designated with a unique thread ID assigned at runtime.
3. Management of different memories: The performance optimization of GPU accelerated applications sometimes depend on data access optimization that includes the proper use of different GPU memory spaces. In this regard, it is important to consider the sizes and access latencies of different GPU memories for efficient placement of different optimization structures on different memories.

Below are the contributions of this research that address the challenges mentioned in section 4.1:

4.2   Efficient cooperation between GPU and CPU

An efficient GPU-CPU cooperation requires sharing the work as well as optimizing data transfer between two components.

 4.2.1 Task repartition on GPU

The iteration level parallel model focuses on the parallelization of each iteration of metaheuristics. Indeed, the most time consuming task in a metaheuristic is the evaluation of the generated solutions. The concerns for the parallelization is the search techniques/mechanisms which are problem independent operations (For example, the evaluation of successive populations for P-metaheuristics and the generation/evaluation of the neighborhood for S-metaheuristics). As the iteration level model does not change heuristic’s behavior, it can be defined as a low level Master Worker model. The following Figure 8 illustrates this Master Worker model. A set of solutions generated by the master at each iteration need to be evaluated. Each worker receives a partition of the solutions set from the master. The solutions are then evaluated by the worker and sent back to the master. In case of S-metaheuristics, the workers can generate the neighbors. Each worker receives the current solution from the master, generates neighbors for evaluation and then return this to master. This model is generic and reusable, since it is problem independent.

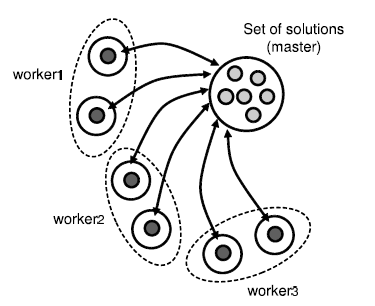Figure 8: The parallel evaluation of iteration-level model.

As mentioned above, the most time consuming task of metaheuristics is often the evaluation of solution candidates. So, in regards with the iteration level parallel model the evaluation of solution candidates should be performed in parallel. According to the Master Worker model, the solutions can be evaluated in parallel with GPU. We can design the iteration level parallel model based on the data parallel SPMD (single program multiple data) model to achieve this. As showed in Figure 9, the main concept for GPU-CPU task partitioning is that CPU is responsible to host as well as execute the whole sequential part of the handled metaheuristic. On the other hand, the GPU is responsible for the solutions’ evaluation at each iteration. The function code in this model called “kernel” to be executed on a number of GPU threads is sent to GPU. The number of threads per block determines the granularity of each partition.

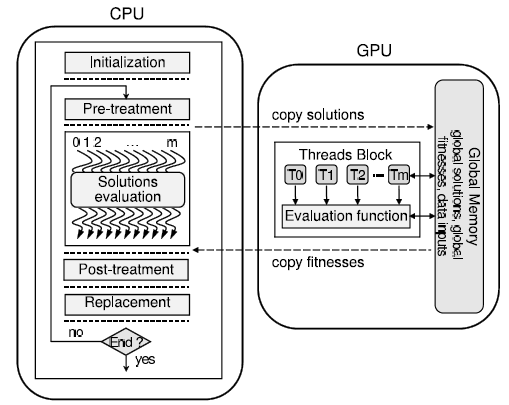Figure 9: The parallel evaluation of solutions on GPU

• Optimization of data transfer

Both GPU and the host computer have their own separate memories and processing elements. So, data transfer between GPU and CPU via PCI bus can be performance bottleneck for GPU applications. A higher volume of data to be copied while repeating the process thousands of times, definitely has a big impact on the execution time. For metaheuristics, the data to be copied are basically the solutions to be evaluated as well as their resulting fitnesses. For most of the P-metaheuristics, the solutions at hand are usually uncorrelated, but for S-metaheuristics each neighboring solution varies slightly compared to the initial candidate solution. So, for parallelization, the data transfers optimization is more prominent in case of S-metaheuristics.

In deterministic S-metaheuristics (such as hill climbing, variable neighborhood search, tabu search), the generation as well as evaluation of the neighborhood can be performed in parallel, which is indeed the most computation intensive. One challenge for data transfer optimization between GPU and CPU is to define where in S-metaheuristics the neighborhood should be generated. Below are two fundamental approaches for this challenge:

• Neighborhood generation on CPU, but evaluation on GPU: The neighborhood is generated on the CPU at each iteration of the search process, and the structure associated with this to store the solutions is then copied to GPU. It is pretty straightforward, as a neighbor representation of a thread is associated automatically with it. Usually this is something that can be done to parallelize P-metaheuristics with GPU. So, in this approach the data transfers are basically: 1) Copying neighbor solutions from CPU to GPU 2) Copying finesses structures from GPU to CPU.
• Both neighborhood generation and evaluation on GPU: The generation of neighborhood happens dynamically on GPU and thereby, there is no need to allocate any explicit structures. A little variation with the candidate solution that generates the neighborhood can be considered as a neighbor. So in this case, only the candidate solution is copied from CPU into GPU. The main advantage is that the data transfers is reduced drastically because only the resulting fitnesses structure need to be copied back from GPU to CPU, but the entire neighborhood does not need to be copied. However, this approach has a problem of determining the mapping between a thread and a neighbor which might be challenging in some cases.

Although the first approach is straightforward, implementing this in S-metaheuristics with GPU will require a large volume of data transfers in case of large neighborhood. This approach can be implemented in P-metaheuristics because the whole population is generally copied from the CPU to the GPU. The first approach might affect the performance because of the external bandwidth limitation. That is why, we consider the second approach i.e. both generation of neighborhood and evaluation on GPU.

The Proposed GPU accelerated Algorithm:

It is not a simple task to adapt traditional S-metaheuristics to GPU. We propose an algorithm 4.2.2 in a generic way to rethink S-metaheuristics on GPU. Memory allocations are made on GPU at the initial stage and also, data inputs as well as candidate solution are allocated initially.

As previously said, heavy computations are required by GPUs with predictable accesses of memory. Hence, we need to allocate a structure to store the results for evaluating each neighborhood fitness’s structure at different addresses. To facilitate the computation of neighbor evaluation, we can also allocate additional solution structures that are problem dependent. The data inputs of the problem, initial candidate solution and additional solution structures need to be copied onto GPU (line#4). The data inputs of the problem are read only structure which doesn’t change at the time of all executions of the S-metaheuristic. So, during all the execution their associated memories are copied for only once. In the parallel iteration level, the neighboring solutions are evaluated and resulting fitnesses are then copied to the neighborhood fitnesses structure (line #6 to #9). The neighborhood fitnesses structure need to be copied into CPU host memory, since it is not defined in which order the candidate neighboring solutions are evaluated (line #10). Then, a particular strategy for the selection of the solution is implemented on the neighborhood fitness’s structure (line #11): CPU explores the neighborhood fitnesses structure in a sequential way. Finally, the chosen solution and additional structures of solution are copied into GPU device memory (#13). This process repeats until some stop criteria is met.

• Additional optimization of data transfer

In some S-metaheuristics, the selection criteria to find the best solution are based on maximal or minimal fitness. So, only one value (maximal fitness or minimal fitness) can merely be copied from GPU to CPU. However, it is not straightforward to find the appropriate maximal/minimal fitness’s, as the read/write memory operations are performed asynchronously. The traditional parallel techniques that strongly suggests the global synchronization of hundreds of threads can decrease the performance drastically.  Therefore, the techniques for the parallel reduction of each thread block should be adapted to address this issue. The following algorithm describes the techniques for the parallel reduction of each thread block.

Algorithm: parallel reduction techniques

Input Parameter: InputFitnesses on Global memory;   1: SharedMem[ThreadId] := InputFitnesses[id] 2: Synchronize locally   3: for n := NumOfThreadsPerBlock/2 ; n > 0; n := n / 2 4:             if ThreadId < n 5:                             SharedMem[ThreadId] := Compare(SharedMem[ThreadId], SharedMem[ThreadId + n]) 6:                             Synchronize locally 7:             end if 8: end for 9: if ThreadId = 0 10:           OutputFitnesses[blockId]:= SharedMem[0] 11: end if Output: OutputFitnesses

One element of input fitnesses from global memory is basically loaded into shared memory by each thread (line #1 and line #2). The array elements are compared by pairs at each iteration of the loop (line #3 to #7). As threads operate on different memory addresses, the maximum/minimum of a given array can be found via the shared memory by applying local threads synchronizations in a given block. We can find the maximum or minimum fitness for all neighbors after a number of iterations are operated on GPU reduction kernel.

In some S-metaheuristics (such as simulated annealing), indeed the best neighbor is selected by the selection of maximal fitness or minimal fitness at each iteration. Therefore, the entire fitness’s structure doesn’t need to be transferred for these algorithms, and also, further optimizations might be possible.

4.3   Efficient control of parallelism

The efficient parallelism control on GPU for the iteration level is mainly focused here. For parallel multithreading in GPU computing, the order for the execution of threads is unknown, since it is indeed hyper threading based. First, it is important to apply the control of threads efficiently in order to satisfy the memory constraints. This allows to improve the overall performance by adding some robustness in the developed metaheuristics on GPU. Second, it is important for S-metaheuristics to define the mapping efficiently between GPU thread and each neighboring candidate solution. Therefore, at runtime each GPU thread is assigned with a unique thread ID for this purpose.

The key components for the parallelism control are the heuristic for controlling threads and the efficient mappings of the neighborhood structures. New S metaheuristics can be designed on GPU by considering these key components. The difficulty arises from the sequential characteristics of the metaheuristics that are first improvement based. In case of traditional parallel architectures, the neighborhood is generally divided into separate partitions with equal size. Then the generated partitions are evaluated and when an improved neighbor is found, the exploration stops. The whole neighborhood doesn’t need to be explored, as the parallel model is asynchronous. When the computations become asynchronous, GPU computing is not efficient to execute such algorithms because GPUs’ execution model is basically SIMD. Moreover, as the execution order of GPU threads is not defined, no such inherent mechanism exists for stopping the kernel in its execution.

We can deal with this type of asynchronous parallelization by transforming these algorithms into a data parallel regular application. So, we can consider the previous iteration-level parallelization scheme on GPU, which means that instead of applying to the entire neighborhood, we can apply to a sub set of solutions which need to be generated and evaluated on GPU. A specific post treatment on this partial set of solutions is performed on CPU after this parallel evaluation. This approach is considered as a parallel technic for simulating the first improvement based S-metaheuristic. Regarding implementation, this is similar to the Algorithm 4.2.2 that is proposed in the previous section. The sub set that has to be handled is the only difference concerns, in which the neighbors are randomly selected. The heuristic of thread control can adjust the remaining parameters automatically once the number of neighbors are set.

Although it may be normal to deal with such an asynchronous algorithm, but compared to an S-metaheuristic this approach may not be efficient, because a full neighborhood exploration is performed on GPU in case of S-metaheuristic. Indeed, memory accesses need to constitute an adjacent range of addresses to get coalesced in order to get a better global memory performance. But this cannot be achieved for exploring a partial neighborhood, because neighbors are chosen randomly.

Figure 10: Illustration of a memory access pattern for both full exploration and partial exploration.

Figure 10 shows a memory access pattern for both full exploration and partial exploration of the neighborhood. In case of full exploration (left side of the Figure), all the neighbors are generated and many thread accesses get coalesced. In case of partial exploration of the neighborhood it does not happen (right side of the Figure), because no connection is available between the elements to get accessed.

4.4   Efficient memory management

For efficient implementation of parallel metaheuristics on GPU, it’s important to understand the hierarchical organization of different memories. However, global memory coalescing can be done for some of the optimization structures which are specific to given GPU thread. This is usually the case for the large local structures that are used in P-metaheuristics for the evaluation function, or organization of data for a population.

Data accesses optimization that includes proper utilization of different memory spaces in GPU is important for optimizing the performance of GPU accelerated applications. The texture memory can certainly provide an amazing aggregation capabilities such as caching global memory. Each unit in texture memory gets some internal memory which buffers data from global memory. We can consider texture memory like a relaxed technique/mechanism of global memory access for the GPU threads, since coalescing is not required to accesses to this memory. For metaheuristics, the utilization of texture memory can be well adapted due to the following reasons:

• As no write operations are possible to perform on Texture memory, it is considered as a read only memory. This memory can be adapted in metaheuristics, because the inputs of the problem are read only values as well.
• In computation of evaluation methods, data accesses are frequent. The texture memory can make some high performance improvement by reducing the number of memory transactions
• In order to provide the best performance for 2D/1D access patterns, cached texture data is laid out. From a spatial locality perspective when the threads of a warp read locations are close together, then the best performance can be achieved. As the inputs of the optimization problems are generally 1D solution vectors or 2D matrices, we can bind the optimization structures to texture memory. Using of texture memories in place of global memory accesses is totally a mechanical transformation.

For parallelizing a metaheuristic, reducing the search time is one of the main goals and also, a fundamental aspect when there are some hard requirements on search time in some types of problems. In this regard, the parallel evaluation of solutions can be a concern for the iteration-level model. It can be considered as an acceleration model for the evaluation of independent as well as parallel computations. This is usually the case of S-metaheuristics that improve a single solution iteratively. There is no direct interaction between different neighborhood moves in these algorithms.

In case of P-metaheuristics, things are little different. During the search process, the solutions that represents a population can cooperate. For example, the solutions that compose the population are selected/reproduced by using variation operators in evolution based P-metaheuristics. A new solution can be constructed with different attributions of solutions which belong to the current population. Participating in constructing a common or shared structure (for example, ant colonies) is another example that concerns P-metaheuristics. The main input for generating the new population of solutions will be this shared structure, and the solutions that are generated previously participate in updating this type of common structure. Unlike S-metaheuristics, P-metaheuristics can provide additional cooperative aspects which is much more important while running multiple metaheuristics in parallel. The challenging issue here is the exploitation of these cooperative properties on GPU architectures.

To the best of our knowledge, these cooperative algorithms are never investigated much for CPU-GPU architecture. For P-metaheuristic, it is indeed the costliest operation to evaluate the fitness for each solution. Therefore, it is important to clearly define the task distribution in this scheme: for each cooperative algorithm the CPU is responsible for managing the whole sequential search process, whereas the GPU is responsible for evaluating the populations in parallel. The CPU sends a set of solutions through the global memory to be evaluated by GPU, and then, these solutions are processed on GPU. The same evaluation function kernel is executed on each GPU thread associated with one solution. Finally, the results of the evaluation function are sent to CPU through global memory.

Algorithm: GPU accelerated Cooperative algorithm for the parallel evaluation of populations

1: Select initial populations 2: Initialize specific variables if needed 3: Allocate problem data inputs, the different populations, fitness’s structures, additional structures of solution on GPU 4: Copy the problem data inputs to GPU 5: repeat 6:            for each P-metaheuristic 7:                            particular pre-treatment 8:                            Copy different populations as well as additional structures of solution on GPU device memory 9:                            for each solution on GPU in parallel 10:                                          Evaluating Solution 11:                                          Adding resulting fitnesses to corresponding fitness’s structure 12:                          end for 13:                          Copy fitness’s structures on CPU (hosts memory) 14:                          particular post-treatment 15:                          Population replacement 16:          end for 17:          Possible transfers between different P-metaheuristics 18: until some stop criteria is met

According to the above algorithm, memory allocations on GPU are made first i.e. problem data inputs, different populations and corresponding fitness’s structures are allocated first (line #3). Additional structures of solution that are problem dependent can be allocated as well in order to make the computation of solution evaluation easier (line #3). Secondly, the data inputs of the problem need to be copied onto GPU device memory (line #4). The structure of these problem data inputs are read only, and also, for all the execution their associated memory need to be copied for one time only. Thirdly, the algorithm mainly describes that at each iteration different populations as well as the associated/ additional structures need to be copied (line #8). Then, the solutions are evaluated on GPU in parallel (lines #9 to #12). Fourthly, the structures of the finesses need to be copied into CPU (#13) and then a particular post treatment as well as population replacement are performed (line #14 and #15). Lastly, a possible migration can be performed on CPU at the end of each generation for information exchange between different P-metaheuristics (line #17). This process repeats until some stop criteria is met.

In this algorithm, GPU is utilized synchronously as a device coprocessor. However, as previously mentioned, copying operations (like population and finesses structures) from CPU to GPU can be a serious performance bottleneck. Accelerating the search process is the main goal of this scheme which does not alter the meaning of the algorithm. Hence, compared to the classic design on CPU, the policy of migration between the P-metaheuristics remains unchanged. This scheme is essentially devoted to cooperative algorithms (synchronous), as the GPU is utilized as a device coprocessor for parallel evaluation of all individuals.

5. Experimental Validation

For our experimental validation, we have considered the following optimization problems to parallelize some heuristic methods with our proposed GPU framework in order to find higher quality solutions.

• Graph Bisection Problem
• Travelling Salesman Problem

5.1    Graph Bisection Problem

For Graph Bisection Problem, we have made experiments to parallelize hill climbing algorithm as well as simulated annealing algorithm with our GPU framework as follows:

5.1.1 Experimental Environment

OpenCL programming environment was setup on a NVIDIA CUDA GPU using C++ as follows:

• NVIDIA CUDA GPU (GeForce GTX 1050 Ti)
• OpenCL Driver for NVIDIA CUDA GPU
• VISUAL STUDIO 2017
• Windows 10 (64-bit Ultimate edition)

Created Visual Studio OpenCL projects (for both Hill Climbing and Simulated Annealing) using Visual C++.

5.1.2 Experimental Data

We’ve considered the following problem for the experiments:

Problem:

Also for experimental validations, various problem instances (such as 20 vertices, 50 vertices, 100 vertices etc.) for graph bisections were used. An example of graph bisections problem for 20 vertices is given below:

0

1 1

0 0 1

0 1 0 0

0 0 0 1 0

0 1 0 1 0 0

1 0 0 0 0 1 0

0 1 0 1 0 0 0 1

1 0 0 0 0 0 1 1 0

0 1 0 0 0 0 1 0 1 0

0 0 0 0 0 0 0 1 0 0 0

0 0 0 0 0 1 1 1 0 0 0 1

0 0 0 0 1 0 1 1 0 0 0 0 0

0 0 0 0 0 0 0 0 0 1 0 0 1 0

1 1 0 0 1 1 0 0 0 1 0 1 1 1 0

1 0 1 0 0 1 0 1 0 1 0 0 0 1 0 1

0 1 0 0 1 0 1 1 0 0 0 0 0 0 0 0 1

0 1 0 0 0 0 0 0 1 0 1 0 0 0 0 1 0 0

0 0 0 0 1 1 1 0 0 0 0 1 0 0 0 1 0 0 0

5.1.3 Experimental Data Presentation and Analysis

Below are the experimental presentation and analysis for both parallel Hill Climbing and simulated annealing algorithm with our GPU framework for Graph Bisection Problem. It is noted that we’ve used the following formula for calculating cut size as explained in section 2 (background).

Data Presentation and Analysis for parallel Hill Climbing

As we ran both CPU based sequential hill climbing and our GPU based parallel hill climbing solution for multiple problem instances (For example: 20 vertices, 50 vertices, 100 vertices etc.) with the above mentioned scenarios and data, we’ve found the following results:

Table 1: Experiment Results for hill climbing algorithm on GPUs

Problem Instance	Best Cost for Sequential Solution	Best Cost for Parallel Solution	Improvement
Graph10.txt	4	3	25%
Graph15.txt	18	13	27.77%
Graph20.txt	25	18	28.00%
Graph30.txt	21	17	23.52%
Graph50.txt	18	15	16.66%
Graph100.txt	30	20	33.33%

We can see from the above results in Table 1 that for each problem instance the GPU based parallel solution got some good improvement on cut size (cost) compared to CPU based sequential solution and thus, the average improvement on cut size (cost) for multiple problem instances is 25.71%. Therefore, much better optimized solution is found for Graph Bisection problem by parallelizing hill climbing algorithm on GPUs.

Data Presentation and Analysis for parallel Simulated Annealing

As we ran both CPU based sequential Simulated Annealing and GPU accelerated parallel Simulated Annealing solution for multiple problem instances ((For example: 30 vertices, 100 vertices etc.)) with the above mentioned scenarios and data, we’ve found the following results:

Table 2: Experiment Results for simulated annealing algorithm on GPUs.

Problem Instance	Best Cost for Sequential Solution	Best Cost for Parallel Solution	Improvement
Graph10.txt	5	5	0%
Graph15.txt	14	13	7.14%
Graph20.txt	19	15	21.05%
Graph30.txt	44	32	27.27%
Graph50.txt	133	60	54.88%
Graph100.txt	663	140	78.88%

We can see from the above results in Table 2 that for each problem instance the GPU based parallel solution got some good improvement on cut size (cost) compared to CPU based sequential solution. Thus, the average improvement for multiple problem instances on cut size (cost) is 31.53%. This improvement looks better when comparatively large problem instances are considered (such as: for 100X100 adjacent matrix, the improvement is 78.88%). Therefore, we can say that we’ve found a better optimal solution as we parallelize Simulated Annealing algorithm with GPUs.

5.2    Travelling Salesman Problem

5.2.1 Experiment Design

We built an experiment environment with the followings:

• CUDA programming model
• C++
• Visual Studio 2017
• NVIDIA GPU (GeForce GTX 1050 Ti)
• CPU (Core i7 9300 quad-core processor)
• Windows 10 (64-bit Ultimate edition)

For experimental validation of Travelling Salesman Problem (TSP), we’ve considered a CPU based sequential solution [29] that we previously proposed at an IEEE conference in 2017. For parallelization with our GPU framework, we’ve considered the following steps:

It is noted that our Main TSP Greedy-Genetic algorithm that we previously implemented for a sequential solution [29] is illustrated in background section. We’ve parallelized the same proposed heuristics with our GPU framework, used the same data and compared the two results to confirm that we find the better optimized solution with GPU.

We developed our simulator by producing the inputs for Euclidean TSP and simplified the simulator with the following assumptions:

• The cities are located on the plane
• The distance between the cities is the Euclidean distance
• Each city is able to reach all other cities

We generated the inputs in such a way that the cities were uniformly placed on a grid at random with 600 columns and 350 rows. Then, by using the columns and rows as unit of Euclidean distance, the path length was obtained after so many numbers of iterations.

5.2.2 Experimental Data Tabulation and Visualization

We made 10+ repeated runs with the same instance in order to observe the behavior of our GPU accelerated parallel TSP solution. Table 3 shows the path lengths for n = 50 cities with 200 iterations. The input for each of this execution was generated randomly as explained above.

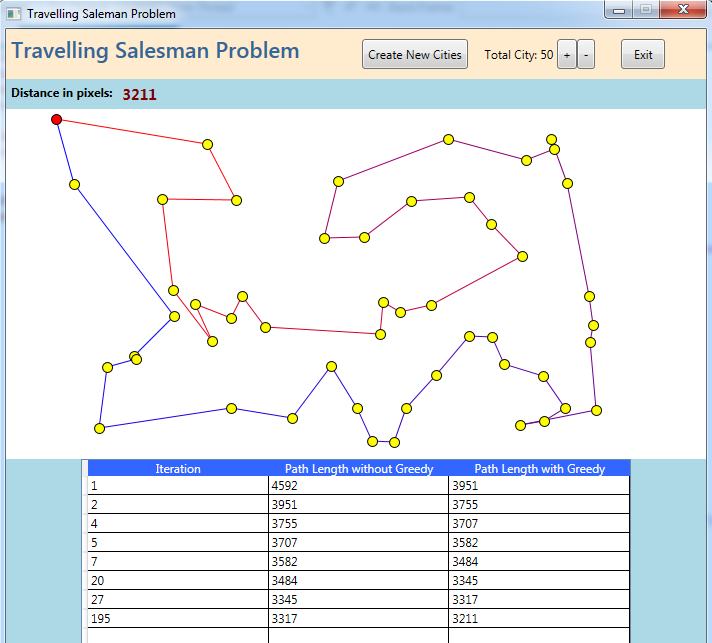
The following visual simulator developed for our previously proposed CPU based solution [29] shows the path length in different iteration levels which finally provide us with one minimum path length after completing all iterations.

We also randomly captured the following GPU thread results from our GPU based parallel solution for one single execution.

Table 3: Path lengths on different GPU threads for TSP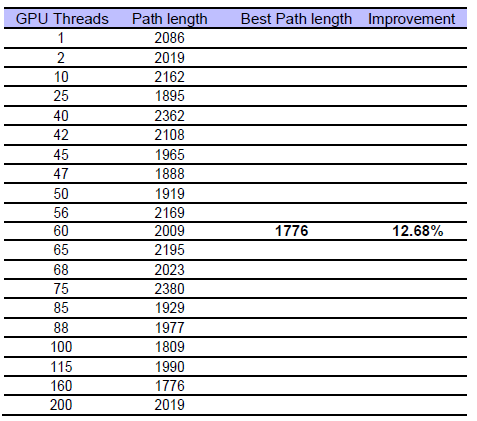

After 10 times repeated run of our TSP heuristics on both GPU and CPU for the same number of cities (n=50), we obtained the following results:

Table 4: Comparison of path lengths between CPU and GPU for TSP

Run#	Path Length (CPU)	Path Length (GPU)	Improvement
1	2034	1776	12.68%
2	1965	1702	13.38%
3	2370	1904	19.66%
4	1881	1607	14.56%
5	2018	1780	11.79%
6	2243	1945	13.28%
7	1980	1756	11.31%
8	1777	1578	11.19%
9	2400	2019	15.87%
10	2018	1745	13.52%

5.2.3 Experiment Result Explanation

In our experimental validation, we involved 200 GPU threads to run the same TSP metaheuristics simultaneously by using our GPU framework. We captured different thread results which is illustrated in Table 4. We can see that the best path length calculated by thread 1 is 2086, thread 2 is 2019, …………, thread 100 is 1809…………, thread 200 is 2019 and so on. As all the thread results are sent to CPU for comparison, CPU finds the best path length (shortest) for TSP is 1776. The average path length obtained from different threads is 2034 and so, the improvement is 12.68% (approximately) because of the parallelization.

As we made 10 times repeated run of our TSP heuristics on both GPU and CPU for the same number of cities (n=50), both results are illustrated in Table 4. We can see that for run#3, CPU based best path length is 2370, whereas GPU best path length is 1904 which is much shorter that CPU based path length and thus the improvement on run#3 is 19.66%. Similarly, if we also observe the results for other repeated runs (#1, #2………#10), we can easily notice that GPU based path length is definitely shorter than CPU based path length and thus there are some improvements in the solution quality for each execution on GPU.

The presented results show that the path lengths are shorter up to 19.66%, with an average of 13.72%. This improvement for finding the shortest path length in TSP is due to GPU parallelization with our framework.

6. Conclusion

In combinatorial optimization, parallel metaheuristic methods can be helpful to improve the effectiveness and robustness of a solution. But, their exploitation might make it possible to solve real world problems by only using important computational power. GPUs are based on high performance computing and it has been revealed that GPUs can provide such computational power. However, we have to consider that GPUs can have many issues related to memory hierarchical management, since parallel models’ exploitation is not trivial. In this paper, a new guideline is established to design parallel meta heuristics and efficiently implement on GPU.

An efficient mapping of the GPU based iteration level parallel model is proposed. In the iteration level, CPU is used to manage the entire search process, whereas GPU is dedicated to work as a device coprocessor for intensive calculations. In our contributions, to achieve the best performance an efficient cooperation between CPU and GPU is very important because it minimizes the data transfer. Also, the goal for the parallelism control is, controlling the neighborhood generation to meet the memory constraints and also, finding the efficient mapping between the GPU threads and neighborhood solutions.

The redesigning of GPU based iteration level parallel model is suitable for most of the deterministic metaheuristics like Tabu search, Hill climbing, Simulated Annealing, or iterative local search. Moreover, we applied an efficient thread control to prove the robustness of our approach. This allows GPU accelerated metaheuristics preventing from crash when a large number of solutions are considered for evaluation. Also, this kind of thread control can provide some improvements with additional acceleration.

Redesigning of the algorithm for an efficient management of the memory on GPU is another contribution. Our contribution is basically the redesigning of GPU accelerated parallel metaheuristics. More specifically, we proposed multiple different general schemes to build efficient GPU based parallel metaheuristics as well as cooperative metaheuristics on GPU. In one scheme, the parallel evaluation of the population is combined with cooperative algorithms on GPU (iteration level). In regards to implementation, this approach is a very generic approach because we only considered the evaluation kernel. However, the performance is little limited in this approach because of data transfer between GPU and CPU. To address this issue, GPU based two other approaches operate on the complete distribution of search process, involving the appropriate use of local memories. Applying such a strategy allows to extremely improve the performance. This approaches might experience some limitations because of the memory limitations with some of the problems which can be possibly more demanding with respect to resources. We have proved effectiveness of the proposed methods with a set of experiments in a general manner.

Furthermore, our experiments show that not only GPU computing exploits the parallelism to improve the solution quality, but also it can speed up the search process. In the future, we’ll try to extend the framework with further features to be validated on a wider range of NP-hard problems in various fields like deep neural network, data science, artificial intelligence, computer vision, machine learning etc. including current industry challenges.

Conflict of Interest

We have no conflicts of interest to disclose.

1.  Dr. Lixin Tao, “Research Incubator: Combinatorial Optimization” Pace University, NY, February 2004
2.  Man Leung Wong, Tien-Tsin Wong, Ka-Ling Fok, “Parallel evolutionary algorithms on graphics processing unit” IEEE Congress on Evolutionary Computation, 2005. https://doi.org/10.1109/CEC.2005. 1554979
3.  Man-Leung Wong,Tien-Tsin Wong, “Parallel hybrid genetic algorithms on consumer-level graphics hardware” IEEE International Conference on Evolutionary Computation, 2006. https://doi.org/10.1109/CEC. 2006.1688683
4.  Ka-Ling Fok, Tien-Tsin Wong, Man-Leung Wong, “Evolutionary computing on consumer graphics hardware” IEEE Intelligent Systems, 22(2), 69–78, 2007. https://doi.org/10.1109/MIS.2007.28
5. Weihang Zhu, “A study of parallel evolution strategy: pattern search on a gpu computing platform” GEC ‘09 Proceedings of the first ACM/SIGEVO Summit on Genetic and Evolutionary Computation, 765–772, 2009. https://doi.org/10.1145/1543834.1543939
6.  Ramnik Arora, Rupesh Tulshyan, Kalyanmoy Deb, “Parallelization of binary and real-coded genetic algorithms on gpu using cuda” IEEE Congress on Evolutionary Computation, 2010. https://doi.org/ 10.1109/CEC.2010.5586260
7.  Shigeyoshi Tsutsui, Noriyuki Fujimoto, “Solving quadratic assignment problems by genetic algorithms with gpu computation: a case study” GECCO ’09 Proceedings of the 11th Annual Conference Companion on Genetic and Evolutionary Computation Conference: Late Breaking Papers, 2523–2530, 2009. https://doi.org/ 10.1145/1570256.1570355
8.  Ogier Maitre, Laurent A. Baumes, Nicolas Lachiche, Avelino Corma, Pierre Collet, “Coarse grain parallelization of evolutionary algorithms on gpgpu cards with easea” GECCO ’09 Proceedings of the 11th An- nual conference on Genetic and evolutionary computation, 1403–1410, 2009. https://doi.org/10.1145/1569901.1570089
9.  Pablo Vidal, Enrique Alba, “Cellular genetic algorithm on graphic processing units” Springer Juan Gonz´alez, David Pelta, Carlos Cruz, Germ´an Terrazas, and Natalio Krasnogor, editors, Nature Inspired Cooperative Strategies for Optimization (NICSO 2010), 2010. https://doi.org/10.1007/978-3-642-12538-6_19
10.  Pablo Vidal, Enrique Alba, “A multi-gpu implementation of a cellular genetic algorithm” IEEE Congress on Evolutionary Computation, 2010. https://doi.org/10.1109/CEC.2010.5586530
11.  Petr Pospichal, Jir ́ı Jaros, Josef Schwarz. “Parallel genetic algorithm on the cuda architecture”, In Cecilia Di Chio, Stefano Cagnoni, Carlos Cotta, Marc Ebner, Anik´o Ek´art, Anna Esparcia-Alc´azar, Chi Keong Goh, Juan J. Merelo Guerv´os, Ferrante Neri, Mike Preuss, Julian Togelius, and Georgios N. Yannakakis, editors, EvoApplications, Springer, 2010. https://doi.org/10.1007/978-3-642-12239-2_46
12. Th´e Van Luong, Nouredine Melab, El-Ghazali Talbi. “GPU-based Island Model for Evolutionary Algorithms. Genetic and Evolutionary Computation Conference” GECCO ’10 Proceedings of the 12th annual conference on Genetic and evolutionary computation, 1089–1096, ACM, 2010. https://doi.org/10.1145/1830483.1830685
13.  Adam Janiak, Wladyslaw A. Janiak, Maciej Lichtenstein. “Tabu search on gpu”, J. UCS, 14(14):2416–2426, 2008.
14.  WZhu, J Curry, A Marquez. Simd, “tabu search with graphics hardware acceleration on the quadratic assignment problem” International Journal of Production Research, 2008.
15.  Th´e Van Luong, Nouredine Melab, El-Ghazali Talbi. “GPU-based Multi-start Local Search Algorithms” Coello C.A.C. (eds) Learning and Intelligent Optimization, Springer, 2011. https://doi.org/10.1007/978-3-642-25566-3_24
16.  Asim Munawar, Mohamed Wahib, Masaharu Munetomo, Kiyoshi Akama, “Hybrid of genetic algorithm and local search to solve maxsat problem using nvidia cuda framework.” Genetic Programming and Evolvable Machines, 10(4), 391–415, 2009. https://doi.org/10.1007/ 978-3-642-25566-3_24
17. Th´e Van Luong, Nouredine Melab, El-Ghazali Talbi, “Parallel Hybrid Evolutionary Algorithms on GPU” IEEE Congress on Evolutionary Computation, 2010. https://doi.org/ 10.1109/CEC.2010.5586403
18.  Man Leung Wong, “Parallel multi-objective evolutionary algorithms on graphics processing units” GECCO ’09 Proceedings of the 11th Annual Conference Companion on Genetic and Evolutionary Computation Conference: Late Breaking Papers, 2515–2522, ACM, 2009. https://doi.org/10.1145/1570256.1570354
19.  Luca Mussi, Stefano Cagnoni, Fabio Daolio. “Gpu-based road sign detection using particle swarm optimization” IEEE Ninth International Conference on Intelligent Systems Design and Applications, 2009. https://doi.org/10.1109/ISDA.2009.88
20.  You Zhou, Ying Tan, “Gpu-based parallel particle swarm optimization” IEEE Congress on Evolutionary Computation, 2009. https://doi.org/ 10.1109/CEC.2009.4983119
21.  Boguslaw Rymut, Bogdan Kwolek, “Gpu-supported object tracking using adaptive appearance models and particle swarm optimization” In Leonard Bolc, Ryszard Tadeusiewicz, Leszek J. Chmielewski, and KonradW.Wojciechowski, editors, ICCVG, Springer, 2010. https://doi.org/10.1007/978-3-642-15907-7_28
22. Simon Harding, Wolfgang Banzhaf, “Fast genetic programming on GPUs” In Proceedings of the 10th European Conference on Genetic Programming, 90–101. Springer, 2007.
23.  Darren M. Chitty, “A data parallel approach to genetic programming using programmable graphics hardware” GECCO ’07 Proceedings of the 9th annual conference on Genetic and evolutionary computation, 1566–1573, ACM , 2007. https://doi.org/ 10.1145/1276958.1277274
24.  William B. Langdon, Wolfgang Banzhaf, “A SIMD interpreter for genetic programming on GPU graphics cards” EuroGP Proceedings of the 11th European Conference on Genetic Programming, 73–85, Springer,2008. https://doi.org/10.1007/978-3-540-78671-9_7
25.  William B. Langdon, “Graphics processing units and genetic programming: an overview. Soft Comput” Springer, 2011. https://doi.org/10.1007/s00500-011-0695-2
26.  Asim Munawar, Mohamed Wahib, Masaharu Munetomo, Kiyoshi Akama, “Theoretical and empirical analysis of a gpu based parallel bayesian optimization algorithm” IEEE International Conference on Parallel and Distributed Computing, Applications and Technologies, 2009. https://doi.org/10.1109/PDCAT.2009.32
27.  Lucas de P. Veronese, Renato “A. Krohling. Differential evolution algorithm on the gpu with c-cuda” IEEE Congress on Evolutionary Computation, 2010. https://doi.org/10.1109/CEC.2010.5586219
28.  Mar´ia A. Franco, Natalio Krasnogor, Jaume Bacardit, “Speeding up the evaluation of evolutionary learning systems using gpgpus” GECCO ’10 Proceedings of the 12th annual conference on Genetic and evolutionary computation,1039–1046, ACM, 2010. https://doi.org/10.1145/ 1830483.1830672
29.  Mohammad Rashid, Dr. Miguel A. Mosteiro, “A Greedy-Genetic Local-Search Heuristic for the Traveling Salesman Problem” IEEE ISPA/IUCC, 2017. https://doi.org/ 10.1109/ISPA/IUCC.2017.00132

(Click Here)

(Click Here)