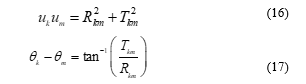1. Introduction

The optimal power flow (FPO) was introduced by J. Carpentier, but it took a long time to become a useful algorithm that could be used as an improvement tool for electrical power systems. For planners and operators, power flow corresponds only to a snapshot of the current state of the network. Planning and operating requirements often require adjustments to the electrical parameters of the system according to a particular criterion [1].

The relaxation techniques allow modeling the problem into a simpler one, facilitating the solution and formulation. In this way, convex relaxation methods have attracted several researches with proposals to simplify and improve the performance of the FPO algorithms in the search for optimal solutions. Relaxation consists on using mathematical transformations to eliminate the power flow terms that introduce the nonconvex characteristic into the optimization problem. The inherent properties of the network are maintained, the output variables of the FPO must also be maintained (however they can be transformed), but the problem becomes more intelligible.

The set of limitations that compound synchronous generator realistic operational bounds is called SGCC. Synchronous machine working as generator base its main features in terminal voltage, field and armature current, power factor and efficiency. Those constraint are rarely take into consideration in OPF formulation, what is extremely dangerous for real operation scenarios leading the machine to operate on overheating conditions and providing inaccurate LMPs information for electric market dealers. Those real limits are extremely useful for network manager, as it will be possible to avoid situations that could offer risks to generator [2].

This work will present a market analysis in locational marginal prices through a non-conventional OPF method using a convex approach from SOCP relaxation, including in it constraints SGCC limits. Text is structured as follows. In the second section will be shown the nonlinear optimal power flow (ACOPF) formulation and it also introduce SOCP relaxation summed up. Section 3 involves the study and equations of SGCC. Simulation and analysis will be found in Section 4. Simulations were held in MATLAB® using its optimization tools for solving both: convex and non-linear OPF.

2. ACOPF Formulation and Relaxation

Optimal power flow is an important tool for planning and operation of system that in its main objective intends to minimize a function of interest referred as objective function and at the same time look for a feasible operation point for power flow equation. It is basically a constrained optimization problem. In its formulation OPF can include also some special devices connected to the grid, using its parameters as control variables, consequently increasing the options for optimization [2].

2.1.  ACOPF Formulation

For original formulation, so called ACOPF, it should be considered a system with the following features:

• A number of lines ;
• A number of buses in wich generators buses,  load buses and normally one slack bus;
• Bus voltage, angle, active and reactive power respectively , , and
• Elements of admittance matrix

Minimizing a generation cost objection objective function  (used for numerical results), as: [2]

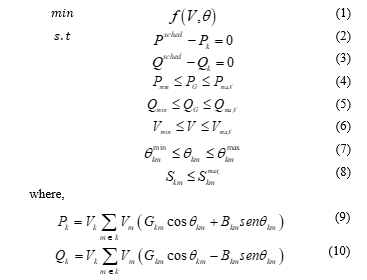For this formulation  bus voltage ( ) and angle ( ) constraints should be concerned. Network constraints are specified in (2) and (3) and its main purpose are find a feasible operation point for power flow. From (4) to (8) are handled systems operational limits, preventing OPF to find a solution that could be not safe for the system. Thus, OPF can minimize a the main function and in parallel return a result for network variables through power flow equations [3].

2.2.   SOCP OPF Relaxation

Non-convexity source in ACOPF model lies on (9) and (10). Therefore, techniques of convexification can be used to relax those equations. References [4,5] show that a simple variable changing in voltage magnitude and phase will make the problem a convex one, as shown in (11)-(13).

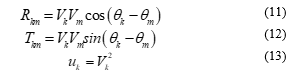Changing  and  in (9) and (10), the follow expressions are reached:

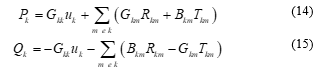Using trigonometric identity and manipulation on (11) and (12), it could be said that:

Constraint (6) becomes:

where,  and .

Taking (11) and (12) it can be noticed that  and  .

Hermitian matrix  can be defined as [6,7]:

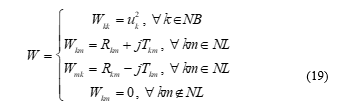Decomposing Hermitian matrix into  submatrix (20) referred as  and making all of them to be semi-definite positive ( ), it could be said that the problem is relaxed as a SOCP problem.

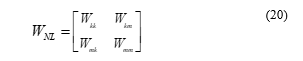3. Synchronous Generator Capability Curve

The capacitance curve (capacity curve or D-curve in other literature) is a selection of important curves for the actual operation of the synchronous generator, with respect to the steady-state analysis. It defines the region of practical operation of the machine, preventing it from operating under overload conditions [8], [9].

The most explored limits in the bibliographies cover only limits of armature current and field. However, other limits are also important for the operation of the synchronous machine, such as mechanical turbine power limits, permanent stability limit and minimum excitation current threshold. [10,11,12]

3.1.  Prime Mover Mechanical Power Limits

Mechanical power limits is verify due the maximum stress that prime-mover can stand without suffer damage in its structure. This constraint will be defined through a constant value on  axis in the diagram. Given a mechanical nominal power for generators turbine the constraints will be:

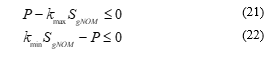where,  and   are constants that weighted mechanical power bounds.

3.2.  Armature Current Limit

This limit can be modeled based on the relation of apparent, active and reactive power. Basically, when machines operate in a constant terminal voltage value, its armature current limits is stablished through its winding thermal limits. So, its noticeable that this constraint is a circumference centered in the origin [2]:

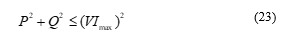3.3.  Field Current Limit

 In the same way when current field is maximum (due its winding thermal limits) and consequently voltage field is maximum, the constraint becomes a circumference centered in :[2]

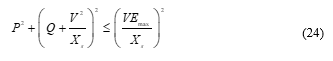3.4.  SOCP-OPF with SGCC Constraints Formulation

Finally including SGCC in SOCP-OPF formulation, concerning that generator is a  bus injecting active and reactive power, but now with its real constraints, formulation becomes:

The number of constraints for ACOPF is ( ) constraints and for SOCP-OPF with SGCC will be ( ). Number of constrains increase in more than two times.

4. Locational Marginal Prices

The new electricity market model adopted around the world had brought a series of advantages regarding services quality, reliability and security for power systems. Indeed, when the market is private and deregulated the competitiveness is much larger enhancing consumer’s electrical energy attendance. Connected systems truly operate more economically and for that reason, sellers and buyers agreed upon a price for a certain number of MWs. Although, each area on the system has its own price, and more specifically each generator has its own one. The concept of LMP allows determining the calculation of nodal price. It can be defined that, LMP for a specific bus is the energy cost needed to supply a  increment of load attending the operational constraints established for the system [9].

In practice LMPs corresponds to Lagrange multipliers on Karush-Kunh-Tucker optimization conditions, for real power equality constraints on OPF.

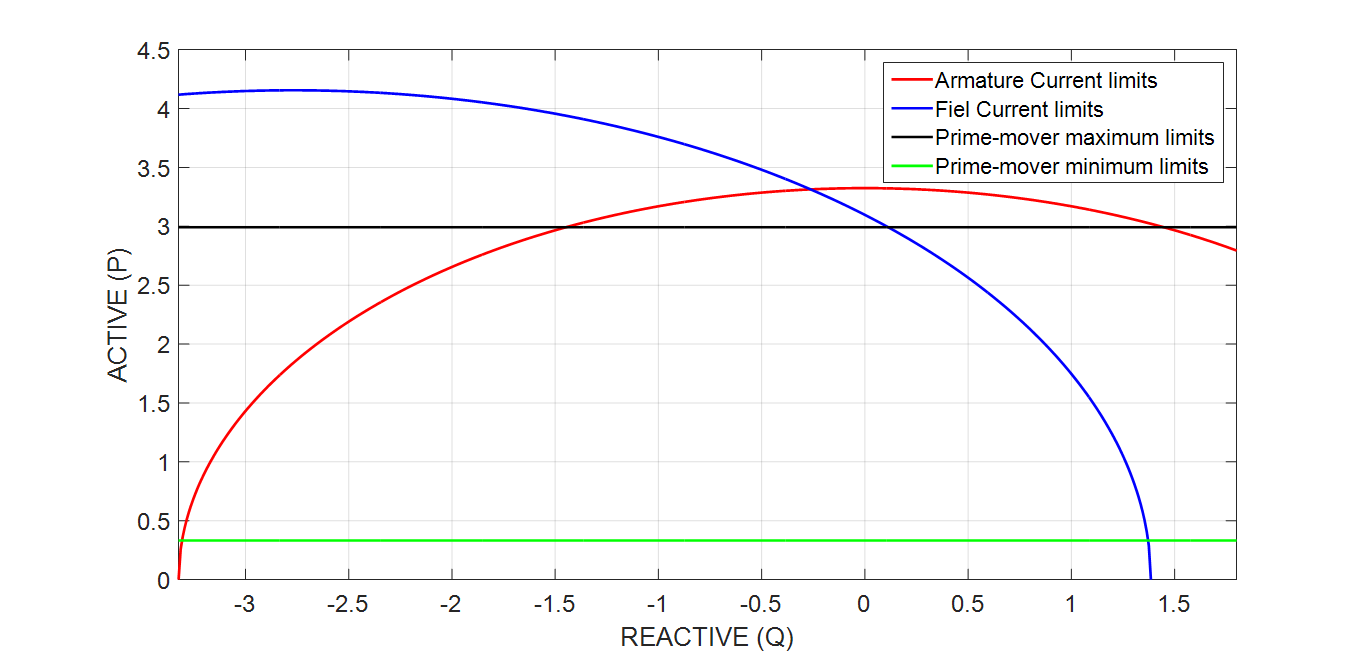Figure 1-Synchrohnous Generator Capability Curve

5. Numerical Results

The proposed method was simulate using IEEE-14 bechmark system [12]. For these four situations were held: ACOPF including or not SGCC, and SOCP-OPF including or not SGCC. For all cases five scenarios of loading were take variating both, active and reactive power. All of them had its main results registered in Table 4. Although just 50%, case base and 150% of loading are specifically analyzed in Table 1-3. Tables register active and reactive powers and locational marginal prices for several situations regarding to a complete analysis.

Table 1- IEEE-14 generators power for Case-base Generator                 N (bus) ACOPF SOCP-OPF Classic SGCC Classic SGCC­ POWER P (MW) Q (Mvar) P (MW) Q (Mvar) P (MW) Q (Mvar) P (MW) Q (Mvar) 1 (1) 194.43 0 – 191.36 -16.11 – 192.99 0 – 190.37 -12.32 – 2 (2) 36.74 11.19 38.3705 36.19 25.25 38.0944 36.63 17.48 38.3132 36.16 28.86 38.0798 3 (3) 28.88 21.58 40.5775 20.6 22.9 40.4121 28.76 23.87 40.5752 21.93 25.1 40.4386 4 (6) 0 14.7 40.1957 10 15.45 39.7982 0 17.49 40.1977 10 16.67 39.871 5 (8) 8.19 19.55 39.6718 10 16.64 39.2565 10.14 13.25 39.6526 10 11.26 39.2879

Simulations were held in an Intel (R) Core (TM) i7-4770S 3.1 GHz, 4-Core and 8GB of memory CPU through a in MATLAB R2015a (8.5.0.197613) using optimization tools for solving the problem

The SGCC for generator connected to systems bus 1 in the 150% scenario is registered in Figure 1. For these constraints, concerned reactive bounds are larger than classical ones.

Optimality gap measures the quality in terms of result for a relaxation process and can be set as [13]:

For classical constrains Optimality gap is around 0.072 and 0.316%. Including SGCC constraint in OPF, values are in a range of 0.16 to 7.5%. In Table 3 computational running time its found to be much greater for SOCP-OPF if compared to ACOPF, when SGCC is included. This implies that solver technology stil needs to be improved for time equality in the process. Comparing just constraints modifications, computational time is not a problem.

Those modifications and adaptations are suggested in [14], [15], and [16].

Possible to make an important note from Table 3:

Table 2- IEEE-14 generators power for 50% case Generator                 N (bus) ACOPF SOCP-OPF Classic SGCC Classic SGCC POWER P (MW) Q (Mvar) P (MW) Q (Mvar) P (MW) Q (Mvar) P (MW) Q (Mvar) 1 (1) 111.89 0 – 85.58 -7.65 – 111.94 0 – 85.61 -3.95 – 2 (2) 20.76 -3.18 30.3807 15.8 1.11 27.8999 20.84 1.4 30.4211 15.86 3.72 27.9276 3 (3) 0 8.49 31.4963 10 7.35 28.6747 0 9.52 31.5674 10 8.32 28.7251 4 (6) 0 -1.1 31.1546 10 -1.78 28.4146 0 -2.42 31.2298 10 -5.6 28.4676 5 (8) 0 -1.23 30.9135 10 -2.08 28.2352 0 5.41 30.9698 10 4.01 28.2692   Table 3- IEEE-14 generators power for 150% case Generator                 N (bus) ACOPF SOCP-OPF Classic SGCC Classic SGCC POWER P (MW) Q (Mvar) P (MW) Q (Mvar) P (MW) Q (Mvar) P (MW) Q (Mvar) 1 (1) 194.43 0 – 191.36 -16.11 – 192.99 0 – 190.37 -12.32 – 2 (2) 36.74 11.19 38.3705 36.19 25.25 38.0944 36.63 17.48 38.3132 36.16 28.86 38.0798 3 (3) 28.88 21.58 40.5775 20.6 22.9 40.4121 28.76 23.87 40.5752 21.93 25.1 40.4386 4 (6) 0 14.7 40.1957 10 15.45 39.7982 0 17.49 40.1977 10 16.67 39.871 5 (8) 8.19 19.55 39.6718 10 16.64 39.2565 10.14 13.25 39.6526 10 11.26 39.2879

• When system load is low, and the system is lightly loaded OPF including SGCC gives a high cost.
• For heavy loading situations classical constraint gives a lower cost.

 This can simply be explained for the fact that reactive limits are larger and minimum mechanical power is greater when taking SGCC approach. In high loading levels the relaxed method has to work hardly to find a feasible solution, and sometimes cannot reach convergence.

LMPs are shown in Tables 1 to 3 for both OPF and for models including or not SGCC constraints. Note that for case-base and 150% loading LMPs practically do not change. Although, for 50% loading case LMPs are lower when OPF includes SGCC.

6. Conclusion

This work exposed a relaxed formulation for Optimal Power Flow including Synchronous Generator Capability Curve constraints, that modeled machines practical bounds. Simulations showed that optimality gap is very short for both formulations. It was shown that for heavy loading levels, relaxed OPF works harder to find a feasible solution. SGCC gives directions for systems operators and planners in respect to availability of active and reactive power plant. Scenarios that SGCC are not concerned could either takes generator to fail in its operations due protection system actuating or damage windings when protection is note involved. Besides, obviously the model that uses SGCC will gives a high LMP, which implies that when it is not considered could offer a fake price for generators power. Results for OPF including SGCC constraint can be analyzed as follow:

• Draw a situation dealing with overprice in light loading scenarios, or;
• Drives the result to a down price in heavily load conditions.

Table 4- ACOPF and SOCPOPF results and computational time Loading Parameters ACOPF SOCOPF Classic SGCC Classic SGCC 50% Cost 3299,60 $/h 3608,20 $/h 3303,50 $/h 3610,50 $/h Time 0,30 s 0,35 s 4,55 s 3,96 s Iterations 20 23 78 125 75% Cost 5522,40 $/h 5646,30 $/h 5533,50 $/h 5653,90 $/h Time 0,30 s 0,26 s 1,85 s 2,07 s Iterations 19 18 71 81 BASE Cost 8079,20 $/h 8084,30 $/h 8095,50 $/h 8100,70 $/h Time 0,29 s 0,36 s 1,80 s 1,94 s Iterations 18 22 73 76 125% Cost 10704,00 $/h 10703,00 $/h 10723,00 $/h 10722,00 $/h Time 0,29 s 0,33 s 3,13 s 1,95 s Iterations 18 21 107 77 150% Cost 13364,00 $/h 13360,00 $/h 13438,00 $/h 13383,00 $/h Time 0,31 s 0,35 s 1,78 s 1,91 s Iterations 20 23 74 77

 Simulation time need to be improved, but this just could be done adjusting the solver technology. That is why it is much larger for the relaxation and still greater when SGCC is included. In these specific cases, LMPs are lower just when loading is 50% of case-base loading, but this situation depends on optimal power flow power limits data.

1.  M. Farivar and S. H. Low, “Branch Flow Model: Relaxations and Convexification—Part I,” IEEE Transactions on Power Systems, vol. 28, no. 3, pp. 2554-2564, Aug. 2013.J. Clerk Maxwell, A Treatise on Electricity and Magnetism, 3rd ed., vol. 2. Oxford: Clarendon, 1892, pp.68-73.
2.  I. G. Fernandes, V. L. Paucar and O. R. Saavedra, “Optimal power flow solution including the syncronous generator capability curve constraints with a convex relaxation method,” 2017 IEEE URUCON, Montevideo, 2017, pp. 1-4. doi: 10.1109/URUCON.2017.8171891
3.  L. S. Vargas, V. H. Quintana and A. Vannelli, “A tutorial description of an interior point method and its applications to security-constrained economic dispatch,” IEEE Transactions on Power Systems, vol. 8, no. 3, pp. 1315-1324, Aug 1993.
4.  R. A. Jabr, “Optimal Power Flow Using an Extended Conic Quadratic Formulation,” IEEE Transactions on Power Systems, vol. 23, no. 3, pp. 1000-1008, Aug. 2008.
5.  R. A. Jabr, “A Conic Quadratic Format for the Load Flow Equations of Meshed Networks,” IEEE Transactions on Power Systems, vol. 22, no. 4, pp. 2285-2286, Nov. 2007.
6. H. Hijazi, C. Coffrin and P. Van Hentenryck, “Polynomial SDP cuts for Optimal Power Flow,” 2016 Power Systems Computation Conference (PSCC), Genoa, 2016, pp. 1-7.
7.  C. Coffrin, H. L. Hijazi and P. Van Hentenryck, “The QC Relaxation: A Theoretical and Computational Study on Optimal Power Flow,” IEEE Transactions on Power Systems, vol. 31, no. 4, pp. 3008-3018, July 2016.
8.  P. Kundur, Power System Stability and Control. New York, NY,USA: McGraw-Hill Professional, 1994.
9.  A. J. Wood and B. F. Wollenberg, Power Generation, Operation, and Control. John Wiley & Sons, 2012
10.  UW-Madison, “Documentation on capability curves,” May 2015, https://neos-guide.org/sites/default/files/capability_curves.pdf
11.  H. Zein and Y. Sabri, “Involving generator capability curves in optimal power flow,” 2015 2nd International Conference on Information Technology, Computer, and Electrical Engineering (ICITACEE), Semarang, 2015, pp. 347-351.
12.  University of Washington, Dept. of Electrical Engineering. Power systems test case archive. Published online at http://www.ee.washington.edu/research/pstca/, 1999. Accessed: 30/04/2012.
13.  C. Coffrin, H. Hijazi, and P. Van Hentenryck, “Network flow and copper plate relaxations for AC transmission systems,” CoRR vol. abs/1506.05202, 2015 [Online]. Available: http://arxiv.org/abs/1506.05202
14. X. Bai, H.Wei, K. Fujisawa, and Y.Wang, “Semidefinite programming for optimal power flow problems,” Int. J. Elect. Power Energy Syst., vol. 30, no. 6, pp. 383.392, 2008.
15.  R. A. Jabr, “Radial distribution load flow using conic programming,” IEEE Transactions on Power Systems, vol. 21, no. 3, pp. 1458-1459, Aug. 2006.
16.  Z. Miao; L. Fan; H. Ghassempour Aghamolki; B. Zeng, “Least Square Estimation-Based SDP Cuts for SOCP Relaxation of AC OPF,” IEEE Transactions on Automatic Control , vol.PP, no.99, pp.1-1

(Click Here)

(Click Here)

No. of Downloads Per Month

No. of Downloads Per Country