1. Introduction

      The paper presents the behavior of slender walls confined masonry buildings, in high seismic areas. The literature points out that slender masonry walls may experience buckling [1] and the axial bearing capacity may be calculated on the deformed shape [2]. Slender walls have less shear force bearing capacity [3]. Confined masonry walls behave well under seismic loading, [4], as the concrete elements increase the energy dissipation, ductility and cracking pattern [5]. Reinforcement bars connecting tie columns to the masonry panels help them work together better [6]. Confining clamps at tie columns tops and bottoms are very important for preventing their shear failure [7]. Masonry walls can behave well in the nonlinear state, as their ductility may be improved by using proper confining reinforced concrete elements [8]. Three dimensional analyses are important as they are able to capture the collapse mechanisms well [9]. Laboratory tests show that confined masonry walls main failing mechanism is diagonal cracking, sliding on the bed joint of brick mortar [10]. It is adequate to analyze a structure’s behavior in the plastic stage, to predict its possible failure mechanism, and the maximum base force it can bear. The moment-curvature diagram may show the ductility or stiffness of the building in study [11]. The structure analyzed here is mostly composed of confined masonry walls, but there are also frames due to the illumination condition. Confined masonry walls are the main bearing elements. The building in study is composed of a ground floor and 2 stories above it. Story height is 4m, and the bays spans are up to 9m, so the masonry walls are very slender. This is a special structure, as nowadays it is most common to use masonry structures with bays up to 5m and story heights up to 3.2m, because masonry is a fragile material and does not behave well under seismic loading. The design codes in force used to design the structure are: [12–18].  The building is a school. It will be built in Bucharest, Romania. This is considered a high seismic area according to the seismic code in force, as the seismic acceleration is 0.30g (g is the gravity acceleration) [18]. The building’s behavior is studied for both elastic and plastic state.

2. Building Description

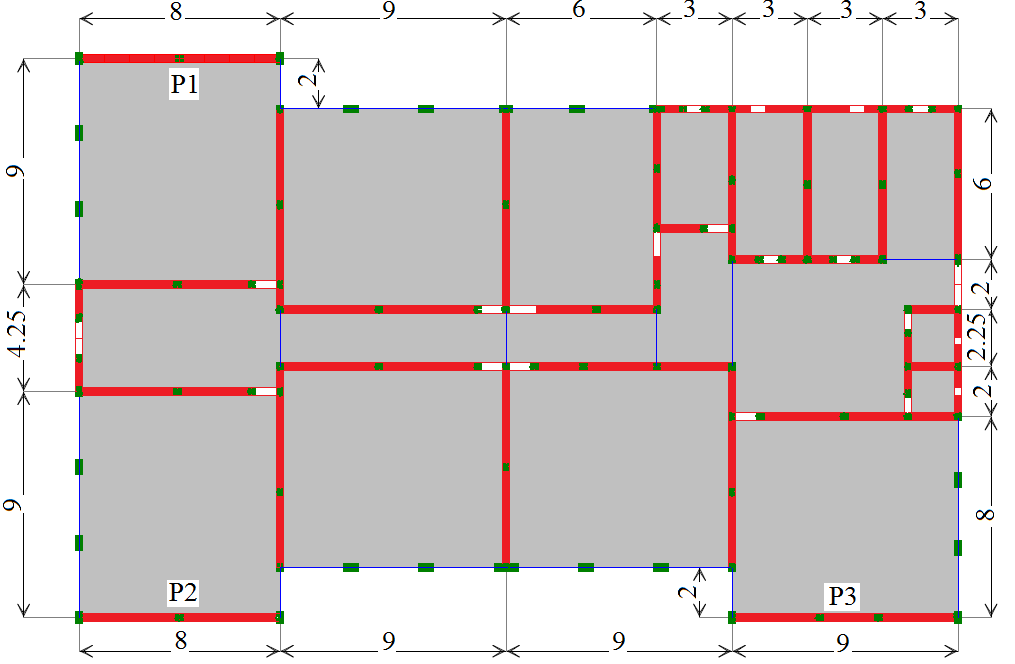
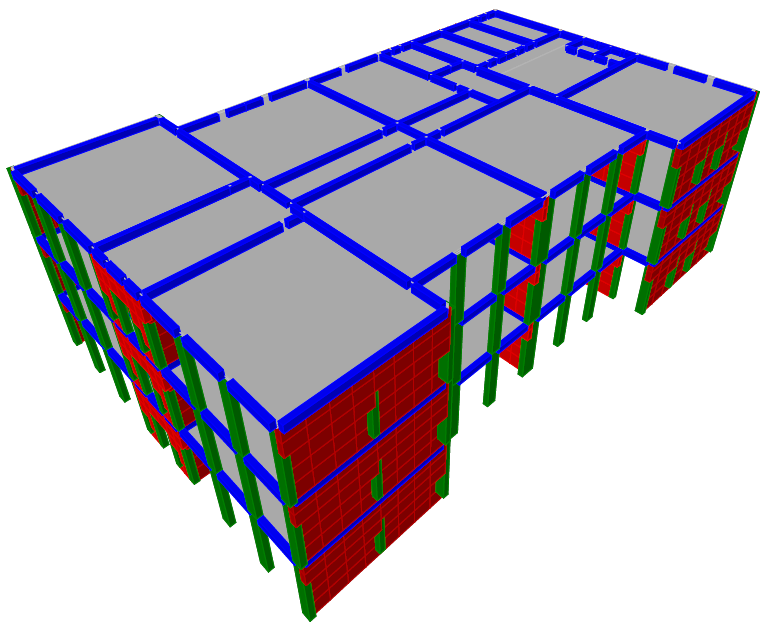
      The structure in study is composed of 3 stories: a ground floor and 2 floors above it. The bays are up to 9m and the story height is 4m. This is regarded as a large bay confined masonry walls building. Confined masonry means that the brick walls are framed by reinforced concrete elements: tie beams (belts) at each story level, placed horizontally and slender columns placed vertically. Those reinforced concrete elements work together with the brick panels. Walls are 30cm thick so the slender columns and the belts need to be 30cm wide. It is allowed to design such buildings in high seismic areas [18]. For confined masonry buildings, in the design code it is recommended to use less strong concrete, class C12/15 or C16/20 [12, 16], because it interacts better with masonry. In Figures 1 and 2 the walls are red, slender columns are green, belts and beams are blue, short beams are white and slabs are grey. This building measures 35m on direction X and 22.25m on Y.  Distances between load bearing elements are given in meters. The software used for analysis is ETABS 2016.

Figure 1 Floor plan

Figure 2 Building in 3D

3. Structure Design Theory

3.1.  Materials Used

Materials used here are: concrete C16/20 with E_C=29000N/mm² (E is elasticity modulus) [16] and vertical perforated bricks 290·140·88 (mm) with E_M=4500N/mm² [12] with standard strength f_b =10N/mm² and mortar M10 [12]. Reinforcement bars are S345 E_S=210000N/mm² [16]. The walls stresses analyzed are: σ_x, σ_z, τ_xz, τ_xy and τ_yz. They are compared to the masonry strengths (1), (2), (3), (4) and (5) [12]. Horizontal design compression strength is f_hd and the vertical one is f_d.

                   f_hd = f_hk/γ_M=0.98/2.2=0.445 N/mm²                    (1)

                            f_d = f_k/γ_M=4.5/2.2=2.04 N/mm²                       (2)

f_hk and f_k are the characteristic masonry compression strengths. γ_M is the insurance factor [12]. Design shear strength for horizontal direction f_vd,l (3) is calculated by using the characteristic strength (f_vk,0) and the unitary vertical stress (σ_d) [12].

       f_vd,l =f_vk,0/γ_M+0.4·σ_d =0.3/2.2+0.4·0.1= 0.18 N/mm²          (3)

Design strength for horizontal and vertical stresses perpendicular to the wall (f_xd1 and f_xd2) are calculated in (4) and (5) using the characteristic strengths (f_xk1 and f_xk2) [12]. Concrete and steel reinforcement bars design strengths are determined in (6) and (7) using the characteristic values (f_ck and f_yk) [16].

                   f_xd1= f_xk1/γ_M=0.24/2.2=0.11 N/mm²                    (4)

                         f_xd2= f_xk2/γ_M=0.48/2.2=0.22 N/mm²                    (5)

                             f_cd=f_ck/γ_M=16/1.5= 10.6N/mm²                        (6)

                           f_yd=f_yk/γ_M=345/1.15=300 N/mm²                      (7)

3.2.  Seismic Action Evaluation

The coefficient c_s is calculated using the base force F_b in (8) according to [18]. γ_I,e = 1.2 is the building’s importance-exposure coefficient, β₀ = 2.5 is the elastic spectrum maximum value, q is the structure’s behavior factor, q=2.25·α_u/α₁= =2.25·1.25 [18], α_u/α₁ = the base shear force value for the failing mechanism/the base shear force value for the first plastic hinge, m = building’s mass, η = 0.88 is the reduction factor according to ξ (damping ratio for masonry) = 8% [16]. λ = 0.85 for 3 stories buildings, a_g = 0.30g [18] and G = building’s weight.

             F_b=γ_I,e · β₀ · a_g· m · λ · η /q =c_s · G =0.24·G [kN]        (8)

3.3.  Walls Bearing Axial Force

The bearing axial force N_Rd for masonry walls is calculated using [12]. N_Rd = wall’s bearing axial force at the bottom story, Φ_i(m)= min (Φ_i ;Φ_m) wall strength reduction factor (buckling factor), Φ_i = wall strength reduction factor at the wall’s top and bottom, Φ_m = wall strength reduction factor at the wall’s center, t = wall thickness, e_i = wall eccentricity at the top and bottom and A= wall section area [12]. The load combination used to determine N_Ed here is: 1.35·permanent loads+1.5·variable loads.

                              N_Rd = Φ_i(m) · A · f_d                                   (9)

                                              Φ_i =1-2·e_i/t                                      (10)

                                  e_i = e_0i + e_hi + e_a ≥ 0.05 · t                          (11)

e_0i= 0, vertical loads eccentricity, e_hm(i)= eccentricity from forces perpendicular to the wall, N₁ = axial load from the upper story wall and N₂ = load from the slabs above the story [12]. M_hm(i) = bending moment from forces perpendicular to the wall, e_a= accidental eccentricity and  h_S = story height [12].

                          e_hm(i) = M_hm(i) /(N₁+ΣN₂)                           (12)

                                 e_a=max(t/30;hs/300;1cm)                          (13)

                                       e_m = 2/3·e_0i+e_hm+e_a                               (14)

Table 1 Walls strength reduction factor at middle story height (Φ_m)

slenderness (hS/t)max	masonry type	relative eccentricity em/t
		0.05	0.10	0.15	0.20	0.25	0.30
15	CM	0.75	0.64	0.53	0.42	0.32	0.22

In Table 1, CM means confined masonry. The maximum walls slenderness allowed is 15 [12]. Φ_m is determined from Table 1, according to h_S/t [12], e_m = wall eccentricity at middle story height and e_hm = eccentricity from forces perpendicular to the wall, at middle story height [12].

3.4.  Walls Bearing Bending Moment

The bearing bending moment M_Rd for masonry walls associated to the design axial force N_Ed [12] is calculated in (15). Walls compressed area is A_C. The bearing bending moment borne by the masonry area is M_Rd(M) (17). y_c is the distance from the wall’s weight center to the compressed masonry area center [12]. The bearing bending moment borne by the slender columns reinforcement at the wall ends is M_Rd(As) (18). The load combination used to determine N_Ed and M_Ed here is: 1.0·permanent loads+0.4·variable loads+1.0·seismic loads.

                      M_Rd = M_Rd(M) + M_Rd(As) [kNm]                      (15)

                                   A_C=N_Ed/(0.85·f_d) [mm²]                           (16)

                                   M_Rd(M) = N_Ed · y_c [kNm]                           (17)

                                  M_Rd(As) =l_s·As·f_yd [kNm]                           (18)

f_yd = 300N/mm² is the reinforcement bars design strength. l_as is the distance between slender columns at the walls ends. As is the slender columns longitudinal reinforcement area. Cc is the compressed area gravity center. C is the wall section gravity center. S is the seismic action [12]. b=n·t and n=f_cd/f_d.

                                              b = t · f_cd/f_d                                      (19)

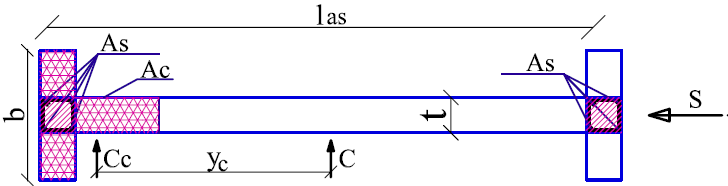Figure 3  Wall horizontal section

4. Building Design Results

The results shown here are story displacements, steel reinforcements in concrete elements and efforts in the walls most vulnerable to seismic action. They are vulnerable because they are slender and not connected to other walls on the other direction, so they are susceptible to fogging.

4.1.  Building Story Displacements

The story displacements will be checked for the elastic state, for both directions X and Y. In the elastic state, the maximum relative story displacements are dr=0.07cm on direction X and dr=0.15cm on direction Y. Maximum displacements are calculated with formulas (20) and (21), considering the building has fragile non-bearing elements, are checked for direction  X (0.098cm< 2cm) in (20) and for direction Y (0.21cm<2cm) in (21). h_S =4m is the story height, ν=0.5 is a reduction factor for class I and II importance buildings and q=2.81 is the structure’s behavior factor [18].  

                        dr ·ν ·q = 0.10cm ≤  0.005 ·h_S=2cm                 (20)

                        dr ·ν ·q = 0.21cm ≤  0.005 ·h_S=2cm                 (21)

4.2.  Reinforcement for Concrete Elements

According to the design results [16], the reinforced concrete elements dimensions and reinforcements are described in Table 2. As is the longitudinal reinforcement in concrete slender columns, belts, columns and beams [16]. The bars are seen in each figure as black circles and the diameter (Φ) of bars is 16mm.

Table 2 Concrete elements reinforcement

Column 30×50 As →8Φ16	Slender column 30×30 As →4Φ16	Column 30×40 As →6Φ16	Column 30×60 As →12Φ16	Beams and belts 30×40 As →8Φ16

4.3.  Confined Masonry Walls Susceptible to Fogging

The most susceptible walls to loss of axial bearing capacity due to buckling are P1, P2 and P3 seen in Figure 1. They are situated on direction X. Those walls are not connected to other walls on the perpendicular direction.

Table 3 Confined masonry walls with high fogging probability

	P1			P2			P3
	NEd [kN]	Φi(m)	NRd [kN]	NEd [kN]	Φi(m)	NRd [kN]	NEd [kN]	Φi(m)	NRd [kN]
story 3	640	0.22	1368	637	0.23	1422	745	0.28	1931
story 2	1289	0.62	3857	1238	0.62	3835	1498	0.64	4413
story 1	1918	0.66	4106	1909	0.86	5319	2231	0.7	4827

5. Building Nonlinear Analysis

Two pushover cases (PX and PY) are used for the building’s nonlinear analysis. Each case determines the building’s stresses and plastic hinges development on an orthogonal direction.

5.1.  Plastic Hinges in Final Stages

Figures 4 and 5 show the final stages of development for plastic hinges on both directions. The color code is the following: B (pink) means the plastic hinge is formed, IO (blue) is for immediate occupancy, LS (light blue) is for life safety, CP (green) is for collapse prevention, C (yellow) means the plastic hinge reaches the limit and the element gives out, D (brown) means the load was redistributed and E (red) means collapse. Those colors are seen in the figures that show the pushover analysis last steps. For both pushover cases, the analysis ends when plastic hinges reach stage D. For PX, there are fewer hinges in stage D. Hinges in stage D are formed at the ends of walls coupling beams. Figures 4 and 5 show the plastic hinges but also the masonry walls as translucent light grey. This is done in order for the figures to be more complete and the masonry walls not to obstruct the plastic hinges visibility.

5.2.  Pushover Diagrams

The pushover diagrams show a stiff behavior on both directions. There are 24 steps for the nonlinear analysis on direction X and 21 steps on direction Y. Some steps are far from each other and some are very close, so they look overlapped. The rigidities remain the same until the structure becomes a mechanism. The structure’s rigidity (base force/top displacement ratio) on direction X is 3806501kN/m, greater than 2269242kN/m for direction Y. The building reaches a higher displacement (143 mm) and a higher base force (545091kN) for direction X.

Figure 4 Plastic hinges for case PX at step 24

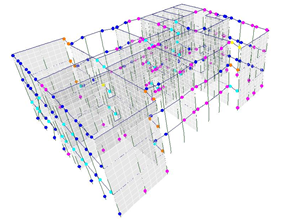Figure 5 Plastic hinges for case PY at step 21

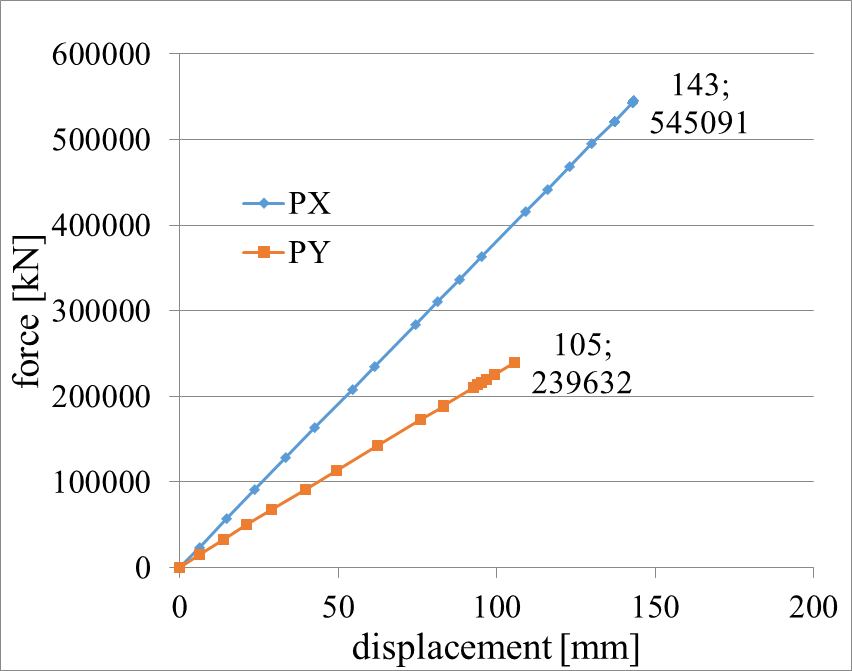Figure 6 Pushover curves for PX and PY

5.3.  Walls Stresses

The maximum value for each stress is written after the analysis step number. The highest values are reached at joints between beams and walls as the stress is transmitted between those elements. There are also increased stress values at the walls corners on the same direction as the pushover case, one corner is crushed and the other is stretched. The maximum value for each stress is written after the analysis step number.

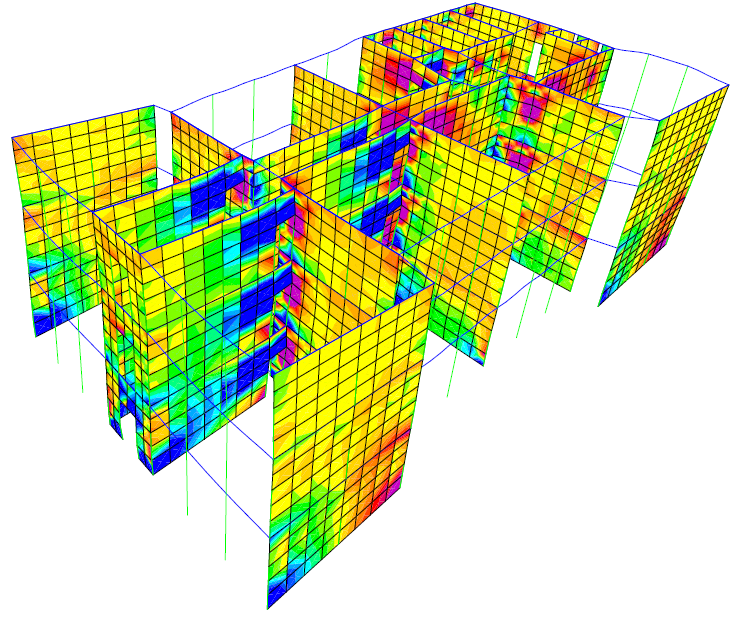Figure 7   PX step 4  σ_x=0.6N/mm²

Figure 8   PY step 6  σ_x=0.6N/mm²

Figure 9   PX step 4 σ_z=2.5N/mm²

Figure 10   PY step 5  σ_z=2.5N/mm²

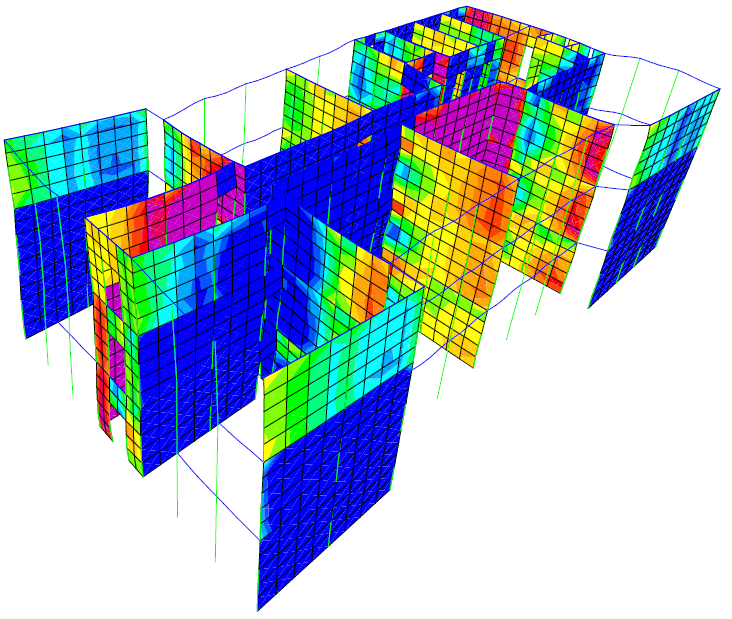Figure 11   PX step 1 τ_xz=0.25N/mm²

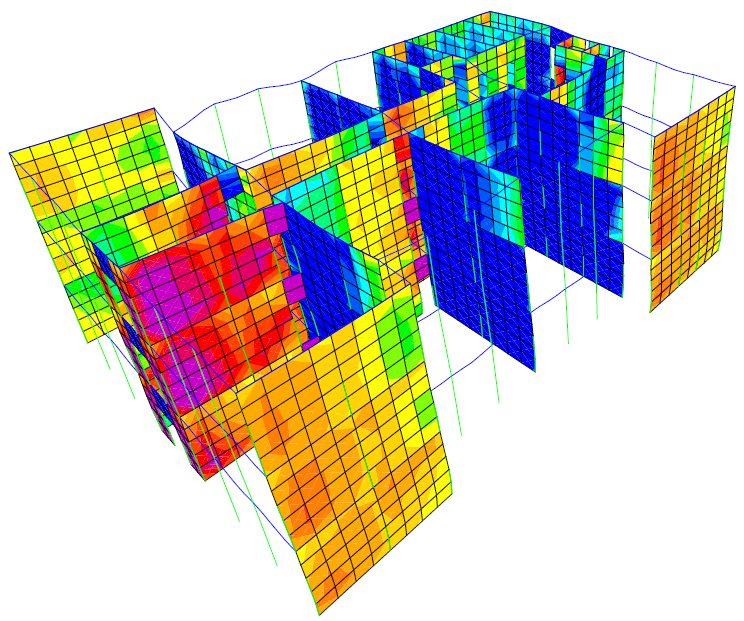Figure 12   PY step 1 τ_xz=0.25N/mm²

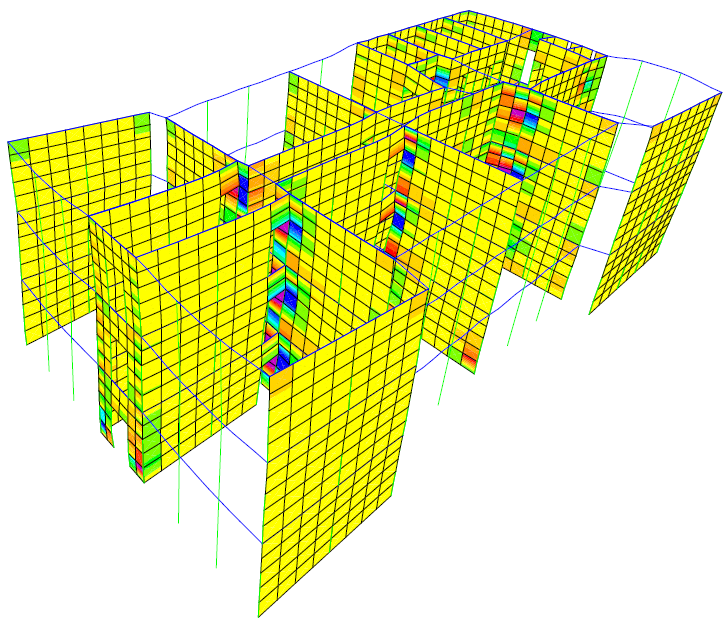Figure 13   PX step 4 τ_xy=0.15N/mm²

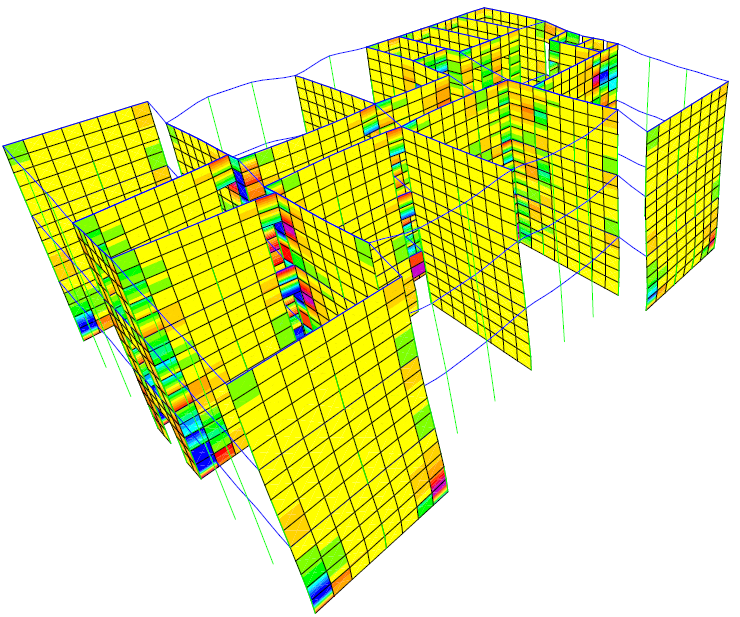Figure 14   PY step 12 τ_xy=0.15N/mm²

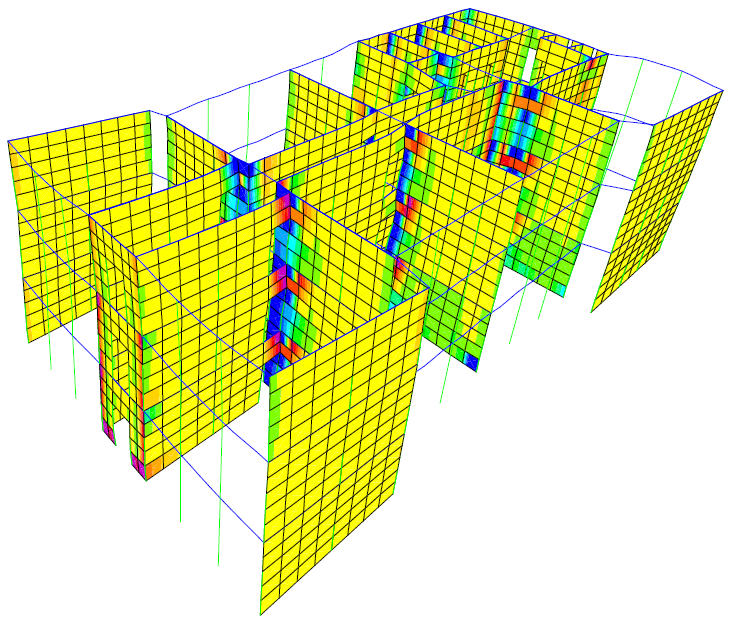Figure 15   PX step 5  τ_yz=0.26N/mm²

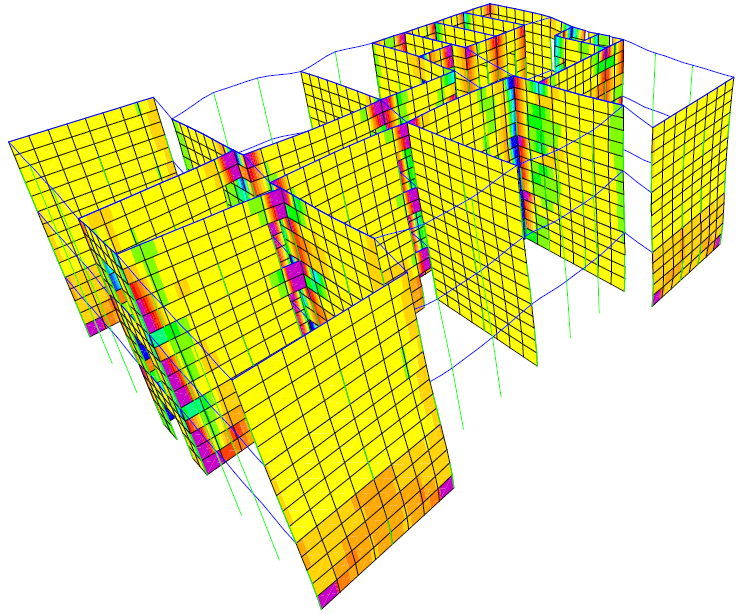Figure 16   PY step 13  τ_yz=0.26N/mm²

6. Discussions

The building has a slender structure and the walls are made of a low strength material. There are 3 walls susceptible to fogging as they are developed on one direction only. The reinforced concrete elements are placed in accordance with the masonry code in force [18]. Additional reinforced concrete bands or lintels and slender columns may be provided in walls. In this latter case, walls would behave less slender. The walls fogging phenomenon would be less visible, as the confined masonry walls would behave more like concrete walls.

The building’s lateral displacements in the elastic stage are lower than the maximum values accepted by [18]. The reinforcement needed for beams, columns, bands and slender columns is within the range demanded by [18]. This means the efforts in concrete elements are within the desired range for the elastic state.

The nonlinear analysis ends when plastic hinges reach stage D for both pushover cases PX and PY. There are more hinges in stage D for PY. Hinges in stage D are seen at the ends of walls coupling beams.  The pushover diagrams show a higher rigidity on direction X. For case PX, the graphic has a higher slope. This slope is calculated as the base force/ top displacement ratio. This ratio is called rigidity. Both diagrams show the same rigidity, as both their slopes remain unchanged until the analysis ends. The analysis ends when the structure is turned into a mechanism by the plastic hinges giving in. The structure gives in at a lower base force and displacement on direction Y. This is explained by the 3 walls susceptible to buckling on that direction. All masonry walls crack before the plastic mechanism is reached. The fogging phenomenon is seen very clearly for stresses σ_x and σ_z.  All masonry walls get local damage from crushing at the bottoms before the structure turns into a mechanism.

7. Conclusions

The building can bear both gravity and seismic loads, although it has a slender structure and the walls are made of a low strength material.

Lateral displacements generated by the seismic combination are allowed by the code in force.

Confined masonry walls developed only on one direction are susceptible of fogging.

In the nonlinear stage the building remains stiff until it turns into a plastic mechanism.

Both pushover diagrams PX and PY are straight lines, so the structure’s rigidity is maintained the same until it collapses.

The structure reaches lower stress values in walls on direction Y.

Conflict of Interest

The author declares no conflict of interest.

1.  C. Cornado, J.R. Rosell, J. Leiva, C. Diaz, “Experimental study of brick masonry walls subjected to eccentric and axial load” RILEM International Conference on Materials, Systems and Structures in Civil Engineering Conference segment on Historical Masonry Technical University of Denmark, Lyngby, Denmark p 33- 40, 2016. www.rilem.net/publications/proceedings-500218
2.  C. Glock, C. A. Graubner, “Design of slender unreinforced masonry walls” 13th International Brick and Block Conference Amsterdam, 2004. No 3 www.hms.civil.uminho.pt/ibmac/2004/
3. J.J. Perez-Gavilan, L.E. Flores, A. Manzano, “A new shear strength design formula for confined masonry walls: proposal to the Mexican code” Tenth U.S. National Conference of Earthquake Engineering Frontieres of Earthquake Engineering Anchorage, Alaska, 2014. July 21-25 https://www.eeri.org/products-page/national-conference-on-earthquake-engineering/10th-u-s-national-conference-on-earthquake-engineering-frontiers-of-earthquake-engineering-proceedings-thumb-drive/
4.  M. Dhanasekar, “Shear in reinforced and unreinforced masonry: response, design and construction” The Twelfth East Asia Pacific Conference on Structural Engineering and Construction , Elsevier Procedia Engineering Vol 14. p 2069- 2076, 2011. doi:10.1016/j.proceng.2011.07.260
5.  A. Marinilli, E. Castilla, “Experimental evaluation of confined masonry walls with several confining columns” 13th World Conference on Earthquake Engineering Vancouver, B.C., Canada paper No. 2129, 2004. https://www.iitk.ac.in/nicee/wcee/thirteenth_ conf_ Canada/
6.  K. Yoshimura, K. Kikuchi, M. Kuroki, H. Nokana, K. Tae Kim, R. Wangdi, A. Oshikata, “Experimental study for developing higher seismic performance of brick masonry walls” 13th World Conference on Earthquake Engineering Vancouver, B.C., Canada; 2004 paper No. 1597, 2004. https://www.iitk.ac.in/nicee/wcee/thirteenth_conf_Canada/
7.  A. Chourasia, S.K. Bhattacharyya, P K. Bhargava, N. M. Bhandari “Influential aspects on seismic performance of confined masonry contruction” Scientific research An academic publisher Natural science Vol. 5. Nr. 8. A1, 2013. http://dx.doi.org/10.4236/ns.2013.58A1007 p56-62.
8.  D. Liu, M. Wang, “Masonry structures confined with concrete beams and columns” 12th World conference on Earthquake Engineering, Auckland, New Zeeland, 2000. http://www.worldcat.org/title/12wcee-2000-12th-world-conference-on-earthquake-engineering-auckland-new-zealand-sunday-30-january-friday-4-february-2000/
9.  A. Alexandris, E. Protopapa, I. Psycharis “Collapse Mechanisms of masonry buildings derived by the distinct element method” 13th World Conference on Earthquake Engineering Vancouver, B.C., Canada paper No. 548, 2004. www.researchgate.net/publication/264850141_Collapse_mechanisms_of_masonry_buildings_derived_by_the_distinct_element_method
10.  W. Wijaya, D. Kusumastuti, M. Suarjana, R. Rildova, K Pribadi “Experimental Study on Wall-Frame Connection of Confined Masonry Wall” The Twelfth East Asia –Pacific Conference on Structural Engineering and Construction Elsevier Procedia Engineering 14 p 2094-2102, 2011 doi:10.1016/j.proceng.2011.07.263
11.  P. Naik, S. Annigeri, “Performance evaluation of 9 story RC building located in North Goa” 11th International Symposium on plasticity and Impact Mechanics, Implast 2016 Elsevier Procedia Engineering 173, p 1841-1846, 2017. doi:10.1016/j.proceng.2016.12.231
12.  CEN EN 1996-1-1-2006 Eurocode 6: Design of masonry structures – Part 1-1: General rules for reinforced and unreinforced masonry structures, 2006.
13.  CEN EN 1991-1-1-2004 Eurocode 1: Actions on structures – Part 1-1: General actions- Densities, self-weight, imposed loads for buildings, 2004.
14.  CEN EN 1990-2004 Eurocode 0: Basics of structural design, 2004
15.  CEN EN 1991-1-3-2005 Eurocode 1: Actions on structures – Part 1-3: General actions- Snow loads, 2005
16.  CEN EN 1992-1-1-2004 Eurocode 2: Design of concrete structures – Part 1-1: General rules and rules for buildings, 2004.
17.  CEN EN 1998-1-2004 Eurocode 8: Design of structures for earthquake resistance. Part 1: General rules, seismic actions and rules for buildings, 2004.
18.  P100-1/2013 Seismic design code – Part 1- General rules for buildings, 2013.

(Click Here)

(Click Here)