1. Introduction

Heat transfer plays a very important role in the living system. This is the complex process, which includes not only some physical factors—conduction, convection, radiation, evaporation but also the physiological factors—blood flow and metabolism. These physical and physiological factors help maintain the constant human body temperature around 37⁰C which is the equilibrium point of the production of heat and loss of heat by the body. The extreme temperatures from the normal body temperature influence the function of biological tissue and the whole system of the body. Death may occur if the body temperature is 27⁰C and below and if 42⁰C and above.  So we should maintain the body temperature around 37⁰C. The heat transfer in the blood vessel also helps to maintain uniform body core temperature regardless of changes in environmental temperature. Metabolism, another important source of heat gain is the chemical process that occurs in the living organism to grow and produce, maintain their structure, and respond to their respective environment [1, 2, 3].

Sweat evaporation is one of the effective parameters in the thermoregulatory process, which is the only way to lose heat when the ambient temperature is higher than the normal body (36.1⁰C – 37.2⁰C) temperature. Due to the sweat evaporation, 22% of heat losses from the body. Evaporative heat exchange also involves the loss of heat through the evaporation of sweat from the skin surface. We generally calculate the rate of sweat evaporation as the weighted mean value of the body core and skin temperature. The reasonable equation for the sweat rate is [4, 5].

      Where  temperature

     and   =    (body core temperature)

It has been proved that the transfer of latent heat from the living being to its environment is often estimated by multiplying the loss in weight attributable to evaporation by the latent heat vaporization of water ‘L’ which decreases from 2501J/g at 0⁰C to 2406 J/g at 40⁰C[6]. Havenith et al.[7] however, have mentioned the values for ‘L’ ranging from 2,398 J/g to 2,595J/ g. and finally suggested the latent heat of evaporation is only dependent on temperature giving a number of 2,430J/g at 30⁰C.

Acharya et al. [5] used variational finite element (FEM) method to prepare one dimensional heat transfer model for the comparative study of temperature profiles of human male and temperature profiles of female luteal and follicular phases of the menstrual cycle.

Havenith et al. [7] studied experimentally by using thermal manikin to determine the effective cooling power of moisture evaporation. They measured both heat loss and mass loss independently by allowing a direct calculation of an effective latent heat of evaporation.

The knowledge of heat transfer is equally important in the field of biomedical research as well as in the treatment of cancer, now a great threat to the existence of humanity. Bioheat transfer models have therapeutic and clinical importance. These models are helpful  for the more effective treatment of cancer than it is now. As per Arkin et al., the effect of hyperthermia treatment depends on the temperature and duration of heating. If a constant temperature could be maintained, the duration of heating would be a reasonable way of expressing thermal dose [8].

Over a hundred years’ time, the effects of the blood flow have been examined on the heat transfer of living tissue. After Bernard came up with an experimental study in 1876, physicians, physiologists, and engineers are interested in the mathematical modeling of the complex thermal interaction between the vascular systems of the body.

In 1948 pennes’ H.H. [9] proposed the simple linear mathematical model based on experimental observation for describing heat flow within the tissue. Many other researchers, one after another, have developed alternative models for describing the perfusion rate and difference between the arterial blood temperature and the local tissue temperature. But Pennes’ model still has an acceptable result to predict the transient temperature due to its simplicity and flexibility [1].

Previous researchers such as Acharya et al. [5], Khandey and Saxena [10], Gurung and Saxena [11], Aijar and Dar [12], Nadel [13] observed the effect of latent heat of sweat evaporation for temperature variation in the human body only by using numerical (Specially FEM) techniques. Numerical methods give the approximation result whereas if the analytic solutions of these equations are attainable, they will give the exact result. Even though the analytical method was used by Yue et al.[2] to solve the model, but this model has not incorporated the effect of Latent heat and sweat evaporation.  The analytical approach for the study of such problems is still lacking. So the present study focuses on a mathematical model of the body temperature based on the Pennes’ bioheat equation due to the sweat evaporation. The temperature at various physical and physiological conditions in the sweating case in comparison with the non-sweating case will be observed in the study

2. Mathematical Model

                The governing differential equation used in the model is given by [9].

Where, ρ = density of tissue (kg/m³), c = specific heat (J/Kg.  ⁰C), K = thermal conductivity (W/m⁰C),  = density of blood (Kg/m³), w_b = blood perfusion rate per unit volume (m³/s.m³), c_b = blood specific heat (J/kg.⁰C), M =  (W/m³.⁰C), S = metabolic heat generation (W/m³), = temperature of arterial blood (⁰C), T = tissue temperature (⁰C).

2.1. Boundary Conditions

Heat loss takes place from the surface of the human body due to convection, radiation, and evaporation because the human body surface is exposed to the environment. So the boundary conditions used in this study is given by

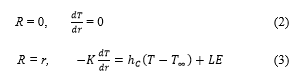Where R is the radius of concerned tissue (m),  is the coefficient of heat transfer on the surface of the tissue (W/m².⁰C), T_∞ is atmospheric temperature (⁰C), L is the latent heat (J/Kg) and E denotes the evaporation rate (Kg /m².sec).

3. Analytic Solution

Being human body cylinder in shape, equation (1) has been converted into the cylindrical form. The one dimensional steady–state equation in the radial direction is expressed as,

To perform the non-dimensionalization of (4) with boundary conditions (2) and (3), we introduce the following characteristic quantities and dimensionless parameters,

Differentiating (5) with respect to ‘r’ then, substituting in (4) we get

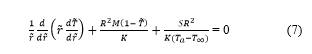 With the use of (6a) and (6b), (7) reduces after calculating to

For computational simplicity, again we put

 = U

= V

 = U – VT

And get the (9) as follows

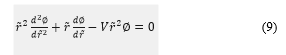This equation is the Modified Bessel’s equation of zero order and comparing it with Modified Bessel equation

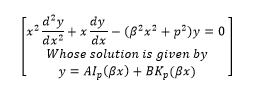  The solution of equation (9) for  can be written as

   Where c₁ and c₂ are arbitrary constants.

After differentiating  with respect to , calculating and substituting the corresponding values with boundary conditions, the solution for and then the solution for T can be written as in (10) and (11).

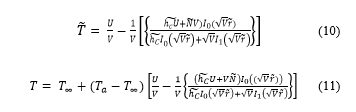Table 1: Thermo-physical parameters [1, 14]

Parameters	Symbols	Values	Unit
Thermal conductivity	K	0.48	W/m0C
Blood specific heat		3850	J/Kg0C
Blood density		1000	Kg/m3
Perfusion rate		3	Kg/s.m3
Metabolism	S	1085	W/m3
Arterial temperature		36.98	0C
Tissue thickness	R	0.03	M
Heat transfer coefficient		10.023	W/m2.0C
Latent heat	L	2400000	J/Kg
Evaporation rate	E	0.00004	Kg/m2.sec
Environmental temperature		30	0C

The effect at various temperature profiles based on the above parameters values are presented graphically and discussed below.

4. Results and Discussions

The analytical solution of the bioheat equation for the cylindrical body and its respective results of physical properties depends on various factors. So the following values of parameters from table 1 have been used in equation (11) to observe the effect of different atmospheric temperature, thermal conductivities, blood perfusion rates, metabolic heat generation, and heat transfer coefficients.

4.1.   Effect of Atmospheric Temperature

              The temperature profiles at a various atmospheric temperature below 37⁰C (normal body temperature) at , , and , and above 37⁰C at , , and , are considered and  shown respectively in Figures 1(a), 1(b) and 1(c), 1(d).

            Although the graphs in both Figures 1(a) and 1(b) show that the body temperature decreases from the core of the body towards the skin surface if the atmospheric temperature is less than the body core temperature, the graphs in Figure 1(b) show that the body temperature decreases more quickly towards the skin surface than in Figure 1(a). This is due to the evaporation effect. On the other hand, if the atmospheric temperature is higher than the body core temperature, the body temperature increases from the core of the body towards the skin surface, which can be seen in Figures 1(c) and 1(d). Moreover, the graphs in Figure 1(d) show that the temperature increases more slowly towards the skin surface than in the graphs in Figure 1(c) due to sweat evaporation, which helps to cool down the body temperature.

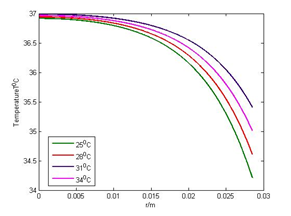Figure 1(a): Effect of  < 37⁰C when E= 0

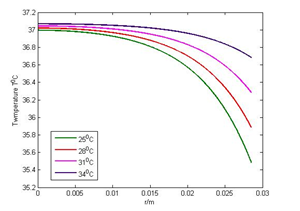Figure 1(b): Effect of  < 37⁰C with LE

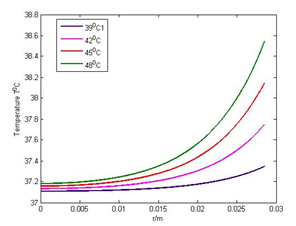Figure 1(c): Effect of  > 37⁰C when E= 0

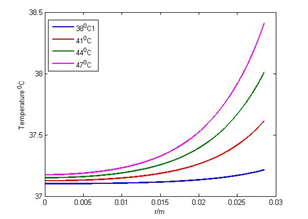Figure 1(d): Effect of  > 37⁰C with LE

4.2.  Effects of Thermal Conductivities

The temperature profiles at various thermal conductivities K = 0.24W/m⁰C, 0.48W/m⁰C, 0.60W/m⁰C and 0.72W/m⁰C are shown graphically in Figures 2(a) and 2(b). With the increase in thermal conductivities, the inner part of body temperature increases but the temperature on the body surface decreases sharply as the thermal conductivities increase. It happens due to the conduction process at the body surface.

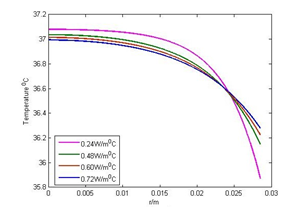Figure 2(a): Effect of thermal Conductivities when E= 0

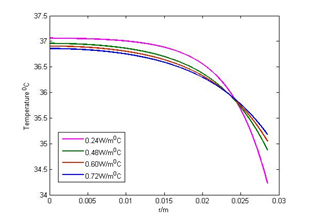Figure 2(b):  Effect of thermal Conductivities with LE

4.3.  Effect of Blood Perfusion

The various values of blood perfusion are taken as  = 1.5 Kg/s.m³, 2 Kg/s.m³, 2.5 Kg/s.m³ and 3 Kg/s.m³ to observe their effect on the temperature of the body. The graphs in Figures 3(a) and 3(b) indicate that the gradient temperature variation in radial direction decreases with the increase of the blood perfusion. Figure 3(b) shows that the temperature falls more sharply towards the surface of the body than in Figure 3(a) because of the evaporation effect together with the blood perfusion.

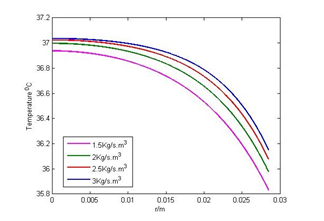Figure 3(a): Effect of blood perfusion when E= 0

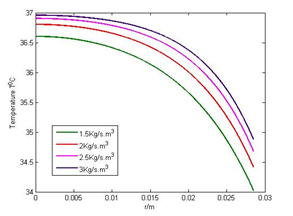Figure 3(b): Effect of blood perfusion with LE

4.4.  Effect of Metabolic Heat Generation

The various values of metabolic heat generation = 141.05 W/m³, 271.25 W/m³, 542W/m³ and 1085 W/m³ are taken. Graphs in Figures 4(a) and 4(b) show that the values of metabolic heat generation have a very small effect on temperature distribution in the human body. The change in metabolic heat from 542W/m³ to 1085 W/m³ make the small change in body temperature almost 0.1⁰C whereas its effect on the skin surface is negligible. This happens due to the negligible concentration of blood vessels towards the skin surface. In the case when sweat evaporation is present (Figure 4(b)), the effect of metabolic heat is almost negligible.

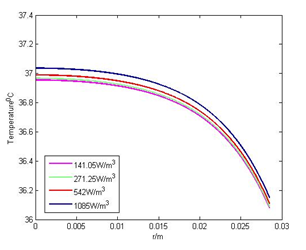Figure 4(a): Effect of metabolism when E = 0

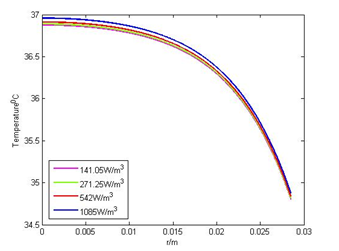Figure 4(b): Effect of metabolism with LE

4.5.  Effect of Heat Transfer Coefficients

The various values of heat transfer coefficients are considered at 5.023 W/m².⁰C, 10.023 W/m².⁰C, 15.023 W/m².⁰C and 20.023 W/m².⁰C. The significant effect of the heat transfer coefficient can be seen in Figures 5(a) and 5(b). The curves in these figures indicate that the gradient temperature in the radial direction decreases with the increase of the heat transfer coefficients.

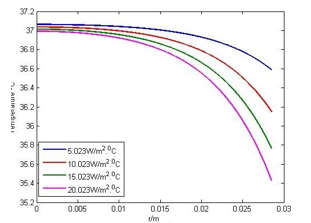Figure 5(a): Effect of   when E= 0

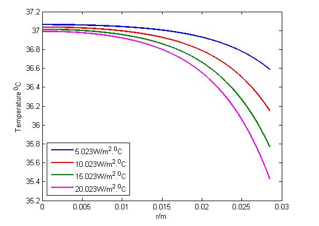Figure 5(b): Effect of with LE

5. Conclusion

In the present study, the analytical solution of the cylindrical form of Pennes’ bioheat equation with boundary conditions including the latent heat of sweat evaporation in the one-dimensional steady-state case is obtained. The effect of the temperature changes in various atmospheric temperature, thermal conductivities, metabolic heat generation rates, blood perfusion rates, and heat exchange coefficients has been observed by using the solution obtained from this model. The study reveals that the atmospheric temperature, blood perfusions, and the heat transfer coefficients have a more significant effect on the temperature variation on the skin surface than in the body core. The gradient temperature in the radial direction decreases with the increase of the ambient temperature, the blood perfusion rates, and the heat transfer coefficients. There is a slight variation in body core temperature even an increase in metabolic heat generation. Its effect on the skin surface is negligible.  The various parameters used in this model have certainly a more remarkable effect on the temperature distribution in the human body than the case suggested in [1, 2]. Such a model may be useful for the researcher as well as thermal diagnosis and hyperthermia treatment of cancer. The analytic solution obtained in this paper can also be extended in the axial and angular direction as well as unsteady state case.

Conflict of Interest

The authors make it sure that there is no conflict of interest.

1.  Kabita Luitel, “Mathematical Model for Temperature Distribution in Cylindrical Human Body” IEEE 2017, 2nd International Conference on Man and Machine Interfacing (MAMI), IEEE 2017.
2.  Yue Kai Zhang, Fan You Xinxin, An Analytic Solution of One – dimensional Steady – state Pennes Bio-heat.Transfer Equation in Cylindrical Coordinates, Journal of Thermal Science, 13(3),52 – 54, 2004.
3. Ahmed Lakhssassi, Kengne, and Emmanuel Semmaoui, Modified Pennes’ equation modeling bio-heat transfer in living tissues: analytical and numerical analysis, Natural Sciences, B, 1375 – 1385, 2010.
4.  Hoppe PR., Heat Balancing modeling, Institute, and Outpatient Clinic for Occupational Medicine, Experientia. 49:741-746, 1993.
5.  Saraswati Acharya, D.B. Gurung, V. P. Saxena, Mathematical Modeling of Sex-Related Differences in the Sensitivity of the Sweating Heat Responses to Change in Body Temperature, British Journal of Mathematics & Computer Science, 12(4), 1 -11, 2016. www.sciencedomain.or.com
6.  Monteith JL., Latent Heat of Vaporization in Thermal Physiology, Nature New Biology 236: 1996, 1972.
7.  George Havenith, Peter Bröde, Emiel den Hartog, Kalev Kuklane, Ingvar Holmer, Rene M. Rossi, Mark Richards, Brian Farnworth, and Xiaoxin Wang, Evaporative cooling: the effective latent heat of evaporation in relation to evaporation distance from the skin, J Appl Physiol, 114, 778 – 785, 2013. doi:10.1152/japplphysiol.01271.2012.
8.  H Arkin., Lx Xu, and K.R Holms, Recent Developments in Modeling, Heat transfer in blood Perfused Tissue, IEEE Transactions on Biomedical Engineering, 41, 97 – 107, 1994.
9.  H.H. Pennes’, Analysis of Tissue and Arterial Blood Temperatures in Resting human forearm, Journal of Applied Physiol, 1, 93 – 1948.
10.  M.A. Khandey and V. P. Saxena, FEM Estimation of One-dimensional Unsteady-State Heat Regulation in Human Head exposed to the Cold Environment, Journal of Biological system, 17, 853 — 863, 2009.
11.  D.B Gurung, V.P Saxena, and P.R Adhikari, Finite Element approach to The one-dimensional Steady-state Temperature Distribution in the Dermal parts with Quadratic Shape Function, J.Appl. Math and information, 27, 301 – 313, 2009.
12.  Mir Aijar and Javid Gani Dar, Mathematical Analysis of Bioheat Equation for the Study of Thermal Stress on Human Brain, Applied Mathematics & Information Sciences and Letters An International Journal, l 5(1), 33 – 39, 2017.
13.  ER Nadel, RW Bullard, JAJ Stolwijk. Importance of skin temperature in the regulation of sweating. J. Appl. Physiol., 46, 430 – 437, 1979.
14.  Lalif M. Jiji, Heat Conduction, 3rd Edition Springer, 52 – 54, 2009.
15.  W.J Minkowycz and E.M, Sparrow Advance in Numerical Heat Transfer Printed in the United States of America, (III), 2009.
16.  Kabita Luitel, D.B. Gurung, Mathematical Model for temperature Distribution in Cylindrical Human Body, The Nepali Mathematical Sciences Report, 3, (1&2), 19 – 28, 2012.
17.  Mir Aijar and M. A. Khanday, Temperature Distribution and Thermal Damage of Peripheral Tissue in Human Limbs During Heat Stress, A Mathematical Model, Journal of Mechanics in Medicine and Biology, 16(2), 16500–16517, 2016.
18.  Ying He, A Numerical coupling model to analyze the blood flow temperature and oxygen transport in Human Breast Tumor and laser irradiation, Japanese Journal of Computers in Biology and Medicine, (2006), 36, P.1336-1350.
19.  D.B Gurung, Saraswoti Acharya, Five Layered Temperature distribution in Human dermal Part. Nepali Mathematical Sciences Report, Central Department of Mathematics, Tribhuvan University, Kirtipur, Nepal, 2011.
20.  D.B Gurung, Kabita Luitel, Development of Bio-Heat Equation and its Application, Proceedings of Nepal Mathematical Society, 85 – 94, 2012.
21.  Mamata Agrawal, Neeru Adlakha, R.K Pardadsani, Modeling and Simulation of the thermal effect of Metastasis Timors in Human Limbs, International Symposium on Devices MEMS, Intelligent system and communication (ISDMISC), 24 – 29, 2011.
22.  Gokul K C, D.B. Gurung, and P. R. Adhikari, Thermal Effect of the eyelid in human eye temperature model, J. App. Math. & informatics 32(5-6), 649 – 663, 2014.
23. Luisiana X. Cundin, William P. Roach, Nancy Millenbaugh, Empirical Comparison of Pennes’ Bio-Heat Equation, Proc. Of SPINE, 7175, 717516-1 — 717516-9.

(Click Here)

(Click Here)