1. Introduction

This work is an extension of previous work [1], which studied the behavior of the scattered field from a conducting cylinder in rotation and translation for the case of TE-mode, i.e. the direction of the incident magnetic field is parallel to the axis of the conducting cylinder. However, the current work concentrates on the scattered field of the moving conducting cylinder in the case of TM- mode, where the direction of the incident electric field is parallel to the axis of the conducting cylinder. Furthermore, a comparison between both modes (TE and TM) is presented herein.

It is known that recent research has focused on the study of different scattering phenomena so as to better evaluate the nature of the scattering body. Historically, the Galilean transformation was used to investigated the effect of the rotation of the conducting cylinder by many researchers [2,3,4]. It was seen from measured results how the behavior of scattered field of the smooth metallic cylinder is affected by rotation. This behavior showed that the incident frequency signal is affected by the rotation of the smooth metallic cylinder. According to the measured results, it is useful to have an analytical expression to explain this phenomenon [5]. The previous work found that the pattern of the scattered field of the rotating cylinder is different in comparison with stationary one especially in the case of TE mode [6,7,8]. In this extensional work, the behavior of the scattered field is investigated, when the polarization of the incident wave is TM polarized form. The expression of the scattered electric field in rotation and translation is found using the Franklin transformation and Lorentz transformation. The new model is used to simulate rotation and translation from stationary static data. Finally, the simulation results of this new model and the previously proposed model [1] are compared.

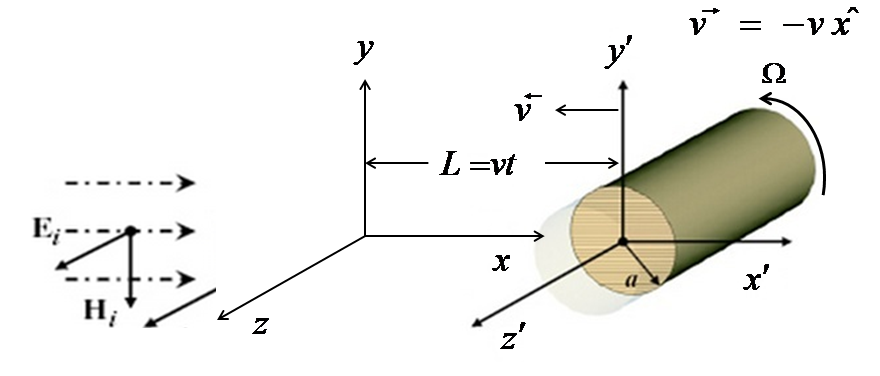Figure 1: TM -mode of the conducting cylinder in rotation and translation

2. Scattering of E-wave (TM-Mode)

Figure 1 shows the description of the problem and the incident electric field is represented by [9]

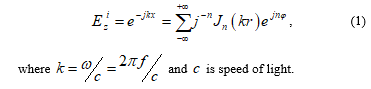In terms of the Franklin transformation, the scattered electrical field from a rotating conducting cylinder is given by [10]

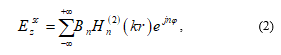where,  is a complex scattering number. This unknown constant number is found using boundary conditions at , where  is the radius of the conducting cylinder [11]

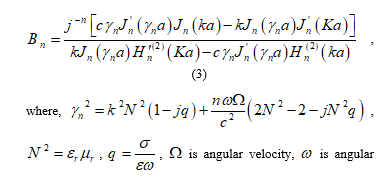where, , , ,  is angular velocity,  is angular frequency, is the conductivity,  is the permittivity, and  is the permeability. In this case, when the conductivity of the cylinder  is very large, goes back to the original expression of the backscattered field of perfect conducting cylinder in the stationary case as [12]

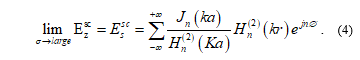      In this step, the approximation to Lorentz transformation is applied to to analyze the phase and magnitude of the backscattered field during translation [13]. The backscattered field of the conducting cylinder in rotation and translation is written as

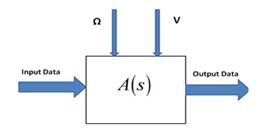
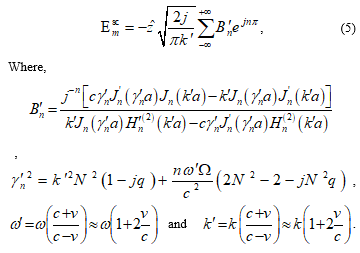The objective of this work is to create a model that simulates translation and rotation of the static data for a complex scatterer as shown in Figure 2. The features of this improved model are written as

Figure 2: Proposed model

where, is the backscattering electric field  of  the perfect conducting cylinder in stationary case [12] and  is a transformation given by

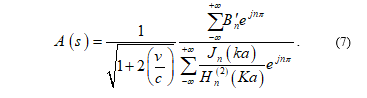The  definition of the model is given by.

3. Comparison of TM and TE modes

It is interesting to compare results of different types of wave polarization (TM and TE). This paper studies the scattered field of the scatterer under rotation and translation when the polarization of incident wave is in TM-polarized form. The result shows that the backscattered field is changed during the translation of the scatterer with the introduction of the term, , as shown in . Moreover, in the case of the TM-mode, the backscattered field is not affected by the rotation of the scatterer as shown in . In the case of TE-mode [1], it was found that the pattern of the phase and magnitude of the backscattered field were affected by the rotation and translation of the scatterer. The effect of rotation shows up with  terms as shown in (4) [1], in addition to the effect of the translation as evidenced by the presence of  terms, similar to the case of the TM-mode. Moreover.  the effect of rotation upon the scatterer is more evident for the TE-mode than the TM-mode. Also, the effect of translation of the scatterer upon the phase and magnitude of the backscattered field is evident in both cases (TM and TE).

4. Numerical Results

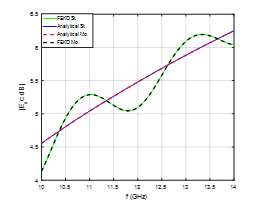
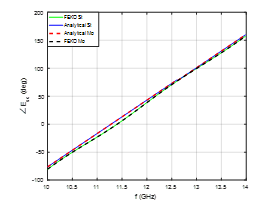
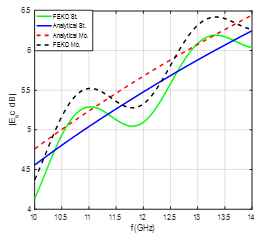
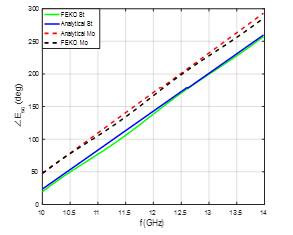
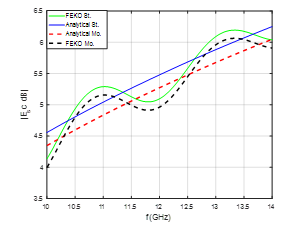
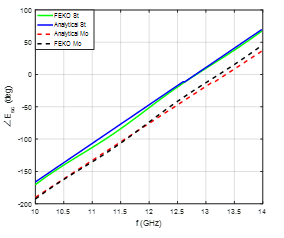
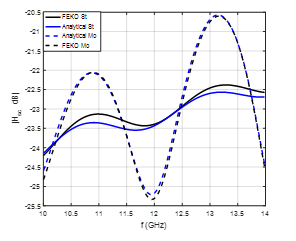
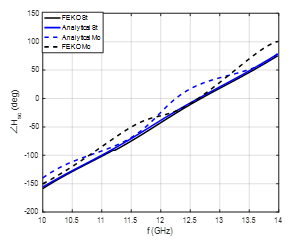
This section includes the simulation results of the new model. The conducting cylinder, which is shown in Figure 1, is modeled using FEKO. It is seen that the incident electric field is z-polarized with the incident plane wave is in the x-direction. It is assumed that the conductivity of the moving cylinder is . The height of the conducting cylinder is  and its radius is . The simulation frequency changed from 10GHz to 14GHz. The static data, generated using FEKO, is inserted into the model as shown in Figure 2 to evaluate the effects of rotation and translation at certain different values of   and , where St and Mo indicate to the stationary and moving cases respectively. Figures 3 and 4 show that the results of both methods are identical and give similar behavior where the slopes of the backscattered magnitudes are equal as shown in Figure 4. Also, the phase and magnitude of the backscattered fields are not affected when the cylinder is rotating with angular velocity and translating with relative velocity . However, after the relative velocity is increased to  and , it is seen that the phase and magnitude of the backscattered field are shifted when the direction of translating cylinder is in the positive x-axis as shown in Figures 5 and 6.  It is important to see the phase and magnitude when the translation of the rotating conducting cylinder is in the opposite direction. It is assumed that the relative velocity of the rotating cylinder is  and  . It is shown the magnitude of the backscattered field is shifted higher in frequency but it has the same slope as shown in Figure 7. The pattern of the phase is shifted lower as shown in Figure 8.

Figure 3: Magnitude of TM at

Figure 4: Phase of TM at

Figure 5: Magnitude of TM at

Figure 6: Phase of TM at

Figure 7: Magnitude of TM at

      The phase of the backscattered fields for TM mode and TE mode is shown in Figures 6 and 10, respectively. It is noted that the effect of rotation of the conducting cylinder is clearly observed by the periodicity in the backscattered phase in the case of TE mode, the period of which increases or decreases when the speed of the rotation decreases or increases respectively as shown in Figure 11 [1]. The effect of the translation is evident in both modes

Figure 8: Phase of TM at

Figure 9: Magnitude of  TE

Figure 10: Phase of TE

(TM and TE) as shown in Figures 5 and 9, and is observed as a shift in the phase and magnitude of the backscattered field. The value of this shift is related to the speed of translation and the direction of the shift is according to the direction of the translation of rotating conducting cylinder. If the translation is along the positive x-axis, the phase is shifted higher as shown in Figures 6 and 10 and the magnitude is shifted lower as shown in Figures 5 and 9.

5. Conclusion

This work studies the effect of the movement of a complex scatterer upon scattering from an incident TM polarized wave. Two types of transformation (Franklin and Lorentz) are used together to analyze the behavior of the phase and magnitude of the backscattered field from the movement of the conducting cylinder.   In the TM-mode case, the backscattered phase increases (shifted higher) and the magnitude of the backscattered field decreases (shifted lower) when the direction of translation is parallel to the direction of the incident wave. When the direction of translation is opposite to the direction of the incident wave, the backscattered phase decreases (shifted lower) and the backscattered magnitude increases (shifted higher). The analytical expression and simulation results show that the effect of rotation of the conducting cylinder on the backscattered field is not evident in the case of TM mode. The result of the comparison between the pattern of the backscattered field for both polarizations (TM and TE) shows that the backscattered phase is affected by the rotation of the conducting cylinder, but this effect is more evident in the TE case. The sinusoidal behavior of the backscattered phase is caused by the rotation of the conducting cylinder, whose periodicity reveals important information about the scatterer. Moreover, the magnitude of the backscattered field is affected by the translation in both polarizations. This effect appears as a shift, according to the direction of the translation of a rotating conducting cylinder. Finally, this study attempts to improve the fidelity of modeling the return of an EM scatterer. An extension of this work is planned that would evaluate the effects of the relative movement of the scatterer upon the scattered field in the case of the oblique incident wave.

1.  E. Abuhdima and R. Penno,“ A New Model for Simulation of Scattered EM fields from a Conducting cylinder in Rotation and Translation using Static Data,” NAECON-OIS, 2017.
2.  D. De Zutter, “Scattering by a rotating circular cylinder with finite conductivity,”IEEE Transactions on Antenna and Propagation, vol. AP-31, No. 1, PP. 166-169, 1983.
3.  P. Hillion, “Scattering by a rotating circular conducting cylinder I, “Mathematical physics, vol. 41, 1998.
4.  P. Hillion, “Scattering by a rotating circular conducting cylinder II, “Mathematical physics, vol. 41, 1998.
5.  John K. Christensen and Michael J. Underhill,“Doppler Measurements of Smooth and Rough Surface High Frequency Scattering from Spinning Steel Cylinders,” IEEE A&E Systems Magazine , 2004.
6. E. Abuhdima and R. Penno,“Simulation of the scattered EM fields from a rotating conducting cylinder,” IEEE International Radar, 2015.
7.  E. Abuhdima and R. Penno,“An Improved Model for the Phase of Backscattered Electromagnetic Fields from a Conducting Rotating Cylinder,” NAECON-OIS, 2015.
8. E. Abuhdima and R. Penno, “Simulation of Scattered EM Field of a Rotating Conducting Number Cylinder using Static Data,” Journal of Energy and Power Engineering, Volume 11, Number 6, June 2017.
9. Harrington, Time Harmonic Elecromagnetic Fields, McGraw-Hill, 1961, pg 234.
10.  Philip Franklin, “The meaning of rotation in the special theory of relativity,” Proc. Nat. Acad. Sci., vol. 8, No. 9, 1922.
11.  E. Abuhdima, “Simulation of the Scattered EM field of Moving Dynamic Object using Static Data,” Ph.D Thesis, University of Dayton, 2017.
12.  C. A. Balanis, Advanced Engineering Electromagnetics, John Wiley &Sons, Inc,( 1989).
13.  E. Abuhdima and R. Penno,“The Effect of Rotation and Translation upon the Scattered EM Fields of a Conducting Cylinder,” NAECON-OIS, 2016.

(Click Here)

(Click Here)