1. Introduction

Successful motivation to learn mathematics cannot be achieved by a simplistic and monolithic approach, since mathematical activity is an innately multidimensional phenomenon. It requires the discriminate attention to a range of motivational factors-namely practical need, creative need, adequate and accurate language facilities, the need for proof, and aesthetic satisfaction.

These can be shown as a triangular hierarchy, mirroring the classic triangle of needs first conceptualized by A. Maslow Figure 1.

At the base of this triangle lies the practical need for solving pressing problems within the realm of day to day human activity. The solution of each of these tasks presupposes the need to generalize the empirical material accumulated in the course of each practical activity, a generalized extraction of certain characteristics common to many objects and phenomena. This is not possible without a definitive leap in the development of human thinking, which marks the emergence of a creative need for the discovery of new facts and patterns that do not belong to the sphere of immediate utility.

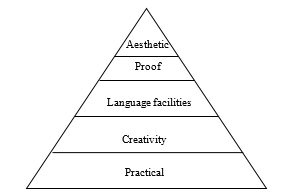Figure 1 Hierarchical model of mathematical activity needs

The historical accumulation of schemes and decision algorithms available for an elementary study of problems necessitated the clarification of terminology and the development of more precise and, at the same time, more symbolic means of presenting these problems than could be achieved using natural language. This encouraged the logical organization of mathematical knowledge in the form of a harmonious deductive theory. At the same time, there was a reassessment of the means for checking the discovered regularities, which, in turn, led to the emergence of the need for their proof using system predetermined postulates and axioms.

Further improvement of mathematical education was achieved through, in particular, attempts to minimize the set of initial assumptions and interpretations of various mathematical theories in such a way that the derivation of new regularities would be seen as elegantly simple, unforced and economical. These attempts were a manifestation of a new aesthetic need to create the perfect expression of the hitherto ad hoc description of motivational factors.

The transition to more advanced levels of the described hierarchy does not invalidate the discrete functioning of the “lower order” needs. On the contrary, these needs are also improved and enriched by entering into productive interaction with the “higher” motivational factors.

These factors are simultaneously present in any mathematical activity. This is especially true for creative needs, which are ideally realized at the initial stage of posing the problem, and then at the subsequent stages of choosing the path of the solution and its justification. The need for proof is clearly expressed at the stage of justifying the decision, and the need for effective language facilities is needed at the stage of formalizing the initial problem. Practical need is especially evident at the stage of problem selection and at the stage of correlating the already obtained result with the limitations provided by the specifics of this problem. Finally, the aesthetic need can potentially be actualized at all these stages, even after solving the initial real situation, by seeking the possibilities of expanding derived and valid mathematical regularity.

The presence of a particular need of the researcher is only a necessary condition for the productive course of mathematical activity. What is also required is the possibility of “objectifying” and internalizing this need into consciously understood motivated activity. This in turn increases practical capacity which in turn can increase conceptual understanding in a virtuous circle.

2. Practice as a source of mathematical creativity

The practical need for the realization of mathematical activity stems from the specific nature of the subject of mathematics as distinct from other scientific disciplines and is embodied in the nature of the interaction of this discipline with reality and public practice. Most scientific disciplines clearly relate to some form of the movement of matter, or to the sphere of individual and social practice, which they study with the help of a variety of methods (including mathematical ones), but, as a rule, remain within their subject area. Mathematics does not set as its immediate goal the analysis of any specific phenomena and processes, but as its raison d’ ere specifically distinguishes the quantitative relations and spatial forms inherent in all subjects and phenomena without exception, and considers them as the purpose and object of its research. Such research is always carried out on the basis of formal approaches “potentially admitting the most diverse material incarnations, and consequently, applications”. In other words, mathematics can be seen as a “universally applicable scientific method”, a kind of generalized “working scheme” for research, description and cognition of nature [1, 2].

This approach has always been associated by specialists in the field of the methodology of science with the general philosophical question of the reasons for the effective value and universality of mathematical theories in solving problems arising in the course of human interaction with the environment. Regular dependencies, expressed by mathematical laws, can be embodied in the intrinsic nature of the objective external world, and we only discover these dependencies through experience and experiment. At the same time, the deductive, speculative nature of mathematical knowledge can reflect its relative isolation from other spheres of human activity. In this latter case the applicability of mathematics to practice can seem bafflingly remote. The first perspective brings to the forefront the external source of the moving forces of mathematics, while the second focuses its attention on the internal needs of the development of this science and its systemic representation.

In actual mathematical activity, both tendencies are almost never presented in isolation. The practice of pure mathematics can subsequently find important practical applications, while results initially assumed to be solely applied do not in fact find any practical applications. So, for example, mathematical logic, which previously mattered only to the persons dealing with the problems of justification, have in recent decades begun to be regarded as an applied science closely connected with computational mathematics. The set-theoretical concept, traditionally perceived as the theoretical foundation of all modern mathematics, is now directly used for the analysis of phenomena of the most diverse sciences – from biology to linguistics [3].

At the same time, it is possible to give examples of so called applied theories, such as the “paint brush theory”, which have no value from either a practical or a theoretical point of view. An interesting example of this nature is suggested by J. Stuart. This author tells about a man who, from general mathematical considerations, derived a very complex formula, filled with constants e, c, h for calculating the radius of the universe. And it was only after many years that scientists decided to obtain by using this formula a specific value of the radius. It turned out that it is equal to 10 centimeters [1].

1. Courant and G. Robbins emphasized that discoveries which simultaneously meet theoretical and practical needs are of particular importance for the further improvement of mathematical knowledge [4]. Thus, for example, the transition from natural to rational numbers served a theoretical need to remove restrictions on the performance of the corresponding arithmetic operations, and also the practical necessity for numbers suitable for the results of measurements of quantities.

In actual mathematical activity, external and internal stimuli, as a rule, are difficult to distinguish. Practice itself often influences mathematics, not only because it immediately requires extensive and profound mathematical knowledge, but also because it can create insights into the unraveling of the mysteries of nature and of the properties and activities of otherwise mysterious configurations. In addition, it is the development of practice certainty, and the need for unambiguous, consistent and correct interpretation of certain natural patterns which has been one of the main motives for developing relatively uniform principles for the systematization and organization of mathematical knowledge, which in turn led to their qualitative transformation and to the formulation of the deductive method.

Let us consider in more detail the manifestation of the stimulating role of practice in relation to mathematical science. The most transparent role is manifested when developing special mathematical methods for solving specific problems that arise in peoples’ real life activities. Among such problems in the early stages of the development of mathematics are the problems of land surveying, the calculation of the volume of vessels, the practical calculation, the calculation of time and the prediction of natural phenomena. Somewhat later, practical changes and developments in, for example, trade, construction and agriculture, combined with new challenges in areas such as astronomy, geography, mechanics, and optics-accelerated the predominant development of computational methods.

A general description of the realization of the relationship between mathematics and practice in similar cases presupposes a sequence of steps, as reflected in Figure 2 below.

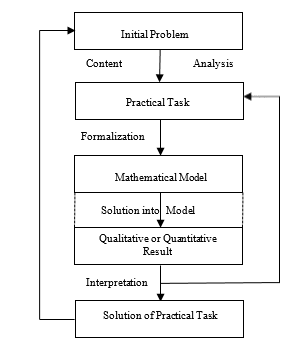Figure 2 The realization of the relationship between mathematics and practice

In accordance with the above Figure 2, a person’s activity in the investigation of one or another side of the real world begins with a meaningful analysis of the initial general problem situation, leading to the formulation of a more specific concrete practical problem. This analysis includes a refinement of the meaning of initially insufficiently defined input parameters; checking the completeness of the initial information and introducing, if necessary, missing data; choosing the range of accuracy and numerical data corresponding to the nature of the problem, and making a preliminary assessment of the value of the problem being solved in relation to the initial problem situation [5].

At the next stage, a mathematical model of the problem is constructed, reproducing the features of the structure and properties of the original in the language of mathematical terms and symbols. Next, the model is transformed, with the aim of obtaining specific numerical values. After correlating these values with the initial situation, a conclusion is made about the plausibility of a given result and the possibility of using the method of obtaining it in solving problems of a similar nature. As an example of this possibility, one can indicate the application in electromagnetism and optics of mathematical methods originally intended for the theory of elasticity [2].

The dominant motivational factor in any considered case is the urgent need to obtain a solution of this particular practical problem irrespective of other possible areas of application of the constructed mathematical model. In such a situation, the effect of this motive essentially ends with the result. A relatively recent example of such a “direct” impact of practice on the development of mathematics is that of linear programming, which arose on the basis of a number of particular problems (optimization of material consumption, organization of transport, etc.) [3, 5, 6, 7].

It should be noted that in the course of the historical development of mathematics, the limiting scope imposed by the way a task was framed has often had a negative effect on the improvement of mathematical knowledge. For example, ancient scientists, in solving the problem of “incommensurable” values, could not overcome the Pythagorean numerical traditions and build mathematics on the basis of pure axiomatic geometry. This resulted, in the words of R. Courant, in one of the “strange wanderings in the history of science”, which for two millennia delayed the “evolution of the idea of number and alphabetic calculus” [1].

A more positive effect of practice on the development of mathematics occurs when mathematical thinking goes far beyond what the posed practical task directly demands, passing successively through a series of steps of abstraction of the concepts and methods from their originally concrete and material prototypes. At the same time, the increasing abstracted purity of mathematical theories simultaneously increases their applicability, so that the range of problems under consideration is broadened and generalized, which, in turn, facilitates the transition of any given theory to a new stage of abstraction. This regularity can be represented schematically in the form of a system of “embedded” plane figures embodying the corresponding levels of abstraction of the practical problems (Figure 3).

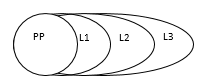Figure 3 The levels of abstraction

We will consider this Figure 3 on the basis of one of the key directions in the development of mathematical science.

In solving the problem of the listing of any objects, each of the individual properties that are available for each of these objects can begin to play the role of a “unit”. A search of these “units” leads to the establishment of a certain sequential order and the emergence of the concept of the ordinal, and then of the quantitative number. The implementation of the simplest operations on numbers convinces us of the need to extend the notion of a number, which has as its final result the creation of a single logical concept of arithmetic.

At the next level of abstraction, it is appropriate to introduce symbols, which imply any quantitative numbers. Thus, we move from arithmetic to algebra and then to mathematical analysis, which unlike algebra studies variables not only in discrete but also in continuous form [8].

The rapid development of theoretical natural science in the late 19th century meant mathematics had also to develop to a new, higher stage of abstraction. In addition to matters of quantitative symbolic content, the mathematical operations themselves are considered to be variables.

The highest level of abstraction of modern mathematics, as already noted above, does not mean its separation from practice. On the contrary, abstract mathematics, operating with such abstract concepts as a group, a set, an abstract space, has managed to explain and express the most complex processes and phenomena of ‘reality’. The application of mathematics to practice is at this level generally realized directly in indirect conjunction with natural science disciplines. As an example, the practice and development of topology produced changes in differential geometry, enriched the theory of relativity and, through the theory of critical points in the calculus of variations stimulated the development of homological algebra, and, through the theory of sheaves and chorology, algebraic geometry. Thus topology has moved from an esoteric category of mathematics to one of its central unifying and basic facets [3].

During the transition through levels of abstraction, mathematics extracts additional information hitherto implicit in its structures, while providing itself with the possibility of continuing applicability to pressing practical demands and also strengthening its internal potential. It should be noted that the initial practical need does not disappear without a trace in the course of its immediate satisfaction. It implicitly participates in the construction of a chain of internal motives for the improvement of mathematical knowledge, reinforced from time to time by direct external impulses. These impulses are due to the classical and ongoing tensions within science between the newly obtained results of experience and observations and the basic laws underlying the corresponding theoretical concept. The solution of these contradictions assumes either the search for new, still unknown methods, or the amendment of the already adopted basic provisions with the aim of increasing the accuracy of their wording through the use of second, third, etc. degrees of approximation. For example, in the early 20th century mathematicians realized that the theory of quadratic forms developed by D. Hilbert was not entirely suitable for solving the problems of rapidly developing quantum mechanics. Awareness of this fact served as a stimulus for J. von Neumann to improve this theory. By refusing the traditional “binding” of a quadratic form to a specific algebraic record, Neumann was able to produce a more general definition which avoided the limitations of the Hilbert approach. This improved theory of quadratic forms was able to provide answers to the very real and specific demands of modern physics [3, 5].

Another possibility of the stimulating effect of practice on mathematics is the transfer of concepts, representations and modes of activity which are characteristic of natural and humanitarian disciplines, to the field of “pure” mathematical science. This possibility stems either from the absence of concepts in mathematics, yet in which language one can describe certain real processes and phenomena, or from the presence of certain discrepancies in the interpretations of “related” objects of study in mathematics and corresponding fields of human knowledge. A change in the viewpoint of mathematical methods makes it possible, in a number of cases, to stimulate the development of a corresponding section of mathematical content. For example, the use of a rigorous definition of the limiting transition in the sense of Augustin-Louis Cauchy in the study of real processes seems at first sight to be impossible, since the consideration of any physical quantities reduced “beyond some reasonable boundaries” is completely meaningless. In connection with this, in physics, the so-called “practical infinitesimal quantities” are considered, and treated as actually infinitesimal. The apparent contradiction is resolved on the basis of a scientifically grounded possibility of using the definition of a limit transition not only for infinite continuous processes, but also for particular cases on bounded sets. Despite this possibility, the practical treatment of infinitesimal quantities has found its application in the concept of nonstandard analysis that goes back to Leibniz, which in a number of cases substantially simplifies the classical exposition of it [4, 6, 9].

Among the existing “channels of influence” of practice on mathematical activity, one more should be mentioned. As we know, practice is the source of plausible reasoning based on intuition, experiment, analogy and constructive induction. These arguments, unlike the proofs, do not provide the reliability of the mathematical theory. However, in them, according to R. Courant and G. Robbins, can be found the real essence of any mathematical discovery, even if it belongs to its most abstract areas [1]. Many examples of how plausible reasoning can lead to the discovery of certain mathematical regularities are given in the well-known work of G. Polya [10]. It is important to note that this author directly relates the application of these arguments to motives that are starting points for the promotion of relevant hypotheses and their proofs.

3. The motivational role of practice for mathematical education in school

The assimilation of a mathematical theory requires consideration of empirical concepts directly related to practical activity. These concepts can also be fully understood, refined and used in practice as meaningful interpretations of abstract theoretical concepts. It is necessary in this respect tо know about the stages in the assimilation of educational material. At the first stage, following observation and experiment, a basis of understanding of a fragment of the mathematical theory is formed. Then, in the course of understanding the whole system of empirical concepts and interrelations between them, knowledge ascends to the theoretical level. Finally, mathematical concepts and methods of activity produce some concrete, meaningful interpretations that make it possible to intensify the students’ desire to apply the acquired theoretical information in practice. This process must of course take into account the overall (and especially age related) context of school based mathematical education.

At the earliest stage, practical activity mainly performs a stimulating function in the study of mathematical content, resulting from the tendency inherent in the child’s initial consciousness to “cling” to specific and directly “tangible” facts and situations [4, 5]. At the same time, the study of mathematics is a process of empirical cognition, in which observation and experiment (calculation, measurement, drawing, construction, etc.) play a major role. The main motivational factor here is the inherent desire of any person to connect the acquired material with their own life and practical experience.

In the following stages of training, the stimulating role of practice, although it ceases to be dominant, nevertheless retains its role as an important means of motivating consideration of a fragment of content and the sparking of initial interest. At the same time, the mathematical fact begins to act not so much as a straightforward step of generalization of empirical material realized by direct teacher guidance, but rather as a result of solving a purely mathematical problem, specially formulated during the consideration of the corresponding practical problem. The possibilities for such work are significantly increased when connecting the material of related subjects, especially physics. Thus, for example, the study of the propagation of light reflected from a specially placed mirror in its path leads to the question of choosing the path by which light travels the shortest distance. An attempt to answer this question leads to the formulation of a purely geometric problem. The solution of this problem is realized, as is well known, on the basis of the symmetry method. Thus, the physical problem appears here as a carrier of motivation for the application of the symmetry method in solving geometric problems.

In another case, observations of sunset followed by plotting the time dependence of the moment of sunset from the date of observation can be used to motivate the introduction of the trigonometric function y=sin x and to reveal some of its features, making it easier for schoolchildren to assimilate such concepts as the domain of function, monotonicity, zeros and the periodicity of the functions [11]. Here, empirical activity does not end with the very introduction of the concept of trigonometric function, but “permeates” the entire content of the topic, periodically providing additional support to the motivational mechanism involved in the initial situation. The main didactic condition for the effective implementation of such situations is the provision during the educational process of the possibility of their detection, awareness and successful resolution.

The participation of schoolchildren in the process of the emergence of new concepts by abstracting and generalizing the phenomena of the real world, significant though it is, by no means exhausts the stimulating potential of practice in the study of mathematical material. In particular, an essential role in the realization of this potential is played by an emerging awareness that knowing a particular fact for solving an important problem, whilst complete in itself, can also lead to the further development of the problem or to proving the theorem. The proposed problem or theorem should always be linked to students’ previous, empirically based experience.

For example, at the primary level students meet challenges to find the sum of certain numbers in a number sequence:

1+2+3+…+99+100

To find the sum students change the order of numbers in the sequence and group them accordingly:

At the senior level, students can apply this fact using geometric material. Here students must find out the number of lines connecting a certain number of points. After some practical actions with two, three, four points, students determine how many lines can be drawn through 100 points. As a result of discussions, students establish that the 100th point can be connected with another point by 99 lines, the 99th point by 98 lines, the 98th point by 97 lines, and so on. This allows a transition from a geometrical problem to an algebraic problem. Further analysis helps to find the number of lines passing through n points. To solve this problem students need to find the sum of the first n natural numbers, i.e. finding the sum of arithmetic progression corresponding to a number sequence.

In the given example, students were stimulated to learn the progression from manipulating geometric objects to formulating a geometrical problems and then converting it into algebraic problem. The use of geometric material gives pupils a subjective feeling of novelty. At the same time it allows them to engage in practical activities.

At the next stage of mathematical preparation, the motivational role of practice is expressed in the realization of its worldview function. Such an implementation is possible through the demonstration of the application of the studied mathematical content in related courses and other school disciplines and consideration of the history of the emergence and evolution of scientific concepts and methods. It also develops familiarity with the elements of mathematical modeling of real states and processes, underlying the mastery of applied mathematical ideology [7, 11, 13]. In addition, an understanding of the role of mathematical knowledge as an important component of human culture becomes one of the leading motivational factors, creating a conscious desire by students to use the acquired material in related subjects and real life practice.

Textual problems are a traditional means of demonstrating the practical importance of mathematics as it is studied in school. In solving them, students become acquainted with the basic l method of cognition of reality via the concept of mathematical modeling of the initial real life situation. They learn to choose which model and how to construct and apply it. They thus also learn how to analyze and interpret the quantitative, graphical or qualitative results they obtain.

Textual problems form part of the very first mathematics lessons, thereby implicitly preparing junior students for a future explicit understanding of the concept of modeling. As a rule, here they act as ‘pseudo-real ‘problems, presupposing exactly as much data as necessary for the solution, and providing for an unambiguous and exact answer. The process of solving such problems is, as it were, “monologist”. It does not require the distinct special definitions and refinements which characterise applied problems of a tangibly external nature [12, 14]. Accordingly, the motivational effect of such tasks is mainly determined by the artificial actualization of problematic situations, often of an entertaining nature, the plot of which to some extent correlates with the real non-mathematical experience of students. The presence of such an effect implies compliance with the following minimum set of requirements.

1. The given tasks must correspond to the real characteristics of the non-mathematical objects described.
2. The task plot should be relatively “close in spirit” to the student, reflecting the significant aspects of his or her experience.
3. The set of mathematical tools mastered by schoolchildren should be sufficient to solve the problem at a level corresponding to this stage of mathematical preparation.

As student mathematical understanding develops, so the possibilities of realizing the worldview function of practice are substantially increased. This is primarily because the set of the subject tools (the types of equations studied, the functional dependencies, algebraic expressions, etc.) are substantially enriched by each of them having the potential to be understood as a mathematical model of some real phenomenon or process. The study of related disciplines (physics, chemistry, geography and others) provides the school mathematics curriculum with a significant number of practical applications and motivations. Mastery of the intrinsic conceptual qualities of mathematical modeling of real processes, studied in related fields of knowledge, provides an understanding of the general possibility of applying mathematical knowledge and skills, and thereby develops enthusiasm for such application. At the same time it becomes the basis for the formation of educationally cognitive motivation both in relation to mathematics itself and in relation to other affected disciplines [15].

It is important to identify a number of conditions for the effective implementation of this ‘worldview‘ function of practice, which apply to all stages of the school based mathematics curriculum.

1. Maximum correlation between the mathematics curriculum and other school disciplines, with close consideration of real life practice. This correlation depends on careful planning and timing, a unity of approach to the formation of concepts common to these courses; consistency of terminology, notation, systems of units of measurement, and also the correspondence of operational structures to the solution of typical problems.
2. Purposeful development of mathematical intuition, implying the introduction of features specific to applied activity in the teaching of mathematics [15, 16]. This includes the basic skills and techniques used in solving practical problems (selection of the necessary data, estimation of the result, methods of approximate calculations, etc.), and the cohesive consistency of the steps characteristic of applied activity (analysis of the real situation, formulation of the problem, choice and construction of its mathematical model, interpretation of the real meaning of the result).
3. Clear demonstration of the origin and development of mathematical concepts and methods because of related knowledge and real life needs and experience.

All this is best achieved within a common ethos and a culture of dialogue within each and across all parts of curriculum. This produces mutually enriching learning within and across disciplines. It is also a matter of positive and sensitive approach. Factors such as emotional tone, confidence in the cognitive abilities of the interlocutor, and mutual support are important examples. Tasks of a practical nature provide great opportunities for developing an iterative dialogue of learning because of their initial empirical uncertainty. The process brings clarity, relevance and priority. Students create a virtuous circle of learning and motivation.

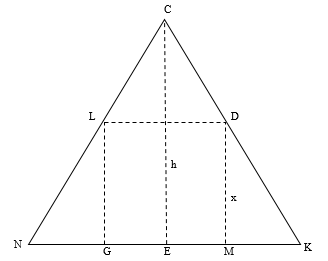
As an example, let us consider a practical problem depicting a real situation associated with the construction of a cottage.

Problem 1.

The cottage has width a = 5 m and length b = 8 m. What is the size of the mansard  if the distance from the attic flooring to the top of the mansard is h = 3 m?

After discussing the meaning of the terms related to the given situation (mansard, attic flooring, top of mansard) students find out that the length of the mansard is the length of the cottage. To find other sizes students analyze the situation and answer the following questions.

1) What geometric shapes correspond to the images of the façade of the cottage and the cross section of the mansard? The answer is a rectangle inscribed in a triangle.

2) When drawing variants of the specified geometrical configuration, when does the mansard becomes the most spacious? Check your answer by calculation. The answer is the rectangle sides are slightly different from each other.

3) How to mathematically characterize the most rational form of the cross section of a mansard? Its area is maximum.

4) What problem can you formulate using this fact? You need to find the maximum cross-section of the mansard.

The problem requirements are not imposed on students by the teacher. They are requirements which develop as an intellectual acquisition as a result of discussion.

Next, some preliminary quantitative estimation of an expected result should be carried out. The estimated value of this result should be determined. Rough approximation shows that the result is equal to the area of the cross section of the mansard which has a triangular shape (15 m²). More precisely, this value is determined through a drawing using students’ visual and intuitive reasoning. This value equals half the cross-sectional area of the mansard approximately (7.5 m²). This process allows students to control the progress of the search.

At the next stage of solving the problem, students’ constructive team work continues. They build a mathematical model. Using the geometrical drawing students formulate a mathematical analog of the practical problem:

Find the sides of a rectangle inscribed in the biggest triangle. The triangle has base a and height h, (Figure 4). Introduce the notation: LD=y; CE= h; DM=LG=x; NK=a

Then students construct an analytical model of this practical problem using similarity of the triangles NCK and LCD:

Where S is the area of the rectangle LDMG.

Figure 4 The mansard

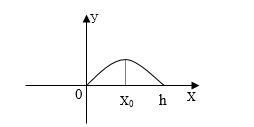
An investigation of the relationship between the area of the rectangle and the second and the third factors (a/h constant) leads to the mathematical question: at what value of x is the product of (h–x)x a maximum (x<h)? This product can be presented in the form  –x² +hx and corresponds to the quadratic function

f(x) = –x² + hx.                                                (1)

Figure 5 Graphical model

In this case only a graphical method is possible. Students construct a new graphical model of this practical problem. This model  is  a  part of   the  parabola   which  opens  downward  (Figure 5). It leads to the next mathematical question. At what argument value is the function f(x) = –x²+hx a maximum?

Clearly the argument value corresponds to the abscissa of the parabola vertex. From the concept of symmetry or the formula this value is

We come to different interpretations of the results.

1. An initial situation.

The maximum cross-section of the mansard is when the height of the mansard is equal to half the distance from the attic flooring to the top, i.e. 1.5 m. The area of the cross-section is

Maximum mansard capacity is

2. A geometrical model.

The side of the rectangle inscribed in the biggest triangle is the middle line of this triangle.

3. An analytical model.

The product of two positive factors has maximum value if they are equal (the sum of these factors is constant).

4. A consequence.

Among all rectangles with the same perimeter, a square has the maximum area.

5. A graphical model.

The relationship between an area of a rectangle inscribed in a triangle and its side is a part of a parabola. The abscissa at the top of the parabola corresponds to the side when an area is maximum. The abscissa of the points of intersection of the parabolas and the coordinate axes corresponds to the side when an area is minimal, etc.

As a result of this work a teachers inform the students that the practical problem considered is one from a wide range of problems where one needs to find maximum and minimum. These problems are of great practical importance. It is useful to give students homework: choose similar problems from their life experience.

This example illustrates all the major stages of solving practical problems.

Among these stages the key element is the choice of the basic model of the studied situation. Practice shows that students have challenges in choosing this model without prompted training activity organized by the teacher. For this to be effective, the teacher must help students develop particular skills. For example, students must establish the similarity between various explanations, to estimate the outcome of each of them in a specific situation, whilst evaluating different approaches. This kind of work can be organized through specially chosen sets of practical problems.

Problem 2

What kind of measuring instruments do you need to determine the area of the steel plate in the form of an equilateral triangle measuring a cm?

Most students propose to use the formula:  for the area of the triangle. It is sufficient to measure the side of a triangle with a ruler. The content of the school physics course allows them to determine the area through the volume and density of the material of the steel plate:   .

Students should weigh this steel plate and find the appropriate value of density in a table. After this activity students get identical results using different formulas and different measuring instruments. The relationship between mathematical and physical reasoning then becomes clear to them.

Students can see that those two approaches produce an approximate measurement. Then they have to explain the equality: . The obtained “motivational impulse” can be used by the teacher to clarify the range of possibilities of the methods used. A teacher gives students steel plates of different forms (a circle, a rectangle, ellipse etc.) and discusses the benefit of different approaches to solve practical problems. The practical approach is optimal for any given activity. Students may see plates of various shapes. Also, they can use the weighing method to determine the characteristics of geometric shapes. This method was successfully applied by Archimedes for the volume of a sphere. During this activity students recognize how a practical method relates to a mathematical method. This method allows students to consider from a given problem how to find areas and volumes of geometrical shapes in general. As a result of this activity students will have long-term motivation in learning future mathematical analysis. It is important to note that in the above (and indeed other) practical problems mathematical activity is not a closed and separated structure; it is a natural component of the universal system of knowledge about the world [9].

4. Students’ orientation in the modern world through solving practical problems

At the last stage of teaching, the role of practice in providing mathematical orientation becomes dominant. Practice gives students a new motivation and understanding of how mathematical skills are needed to fully participate in the modern world and for the successful implementation of future professional activity. However, this is not always easy. One challenge is that many modern scientific fields operate in such a way that their types of models do not smoothly integrate with the traditional mathematics curriculum. More subtle approaches might be then needed to impart an understanding of the practical application of mathematical knowledge to future professional development and in relation to environmental and other extracurricular activities.

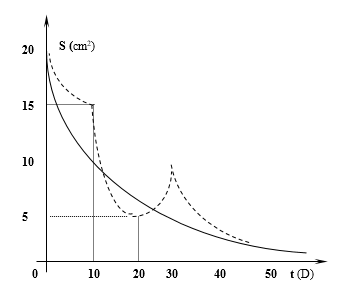
Let us consider an example from the field of medicine. In studying the exponential function in the school, students’ attention is drawn to the traditional formula expressing the laws of growth (y=e^kx) and decay (y=e^–kx). At the beginning of the 20th century American scientists revealed the law related to the latter formula. It reflects the approximate dependence of the area of protracting wounds from the time when the wound becomes sterile. This dependence can be traced with a special device, a planimeter. A planimeter is used for approximate measurement of the surface area bounded by lines. The perfect curve of wound healing is described by the formula: S=S1e–kt, where S1 is the wound area at the initial time. The perfect curve is also called the prediction curve. A prediction curve is compared with an actual curve (Figure 6). The wound is infected if the observed wound area is larger than the area defined by the perfect curve. If a wound heals faster than the perfect curve shows, this indicates the appearance of secondary ulcers. A wound is healing well if the prediction curve is the same as the actual curve.

Such examples, as shown in our monitoring of the teaching-learning process, significantly enhance the general attractiveness of mathematics for students and across disciplines.

Figure 6 Graph of curves

Based on the previous discussion, the motivational characteristics of practical problems can be presented in a systematic form in Table I.

Table 1: Systematic form of practical problems

Stage	Role of practical problem	Motivating factor	Objective	Instructional techniques	Students’ activity
1	Stimulate students’ interest	Intention to link learning material with their own life experiences	Deriving of mathematical relations; understanding concepts, theorems, algorithms and their application	Organization of empirical support for students’ activity	Using students’ life experience, applying it to solve non-standard word problems
2	Develop students’ world outlook	Intention to apply mathematical material which was studied in other related school disciplines and real-life practice	Demonstration of practical application of mathematics in various branches of human knowledge	Forming of modeling method	Using plausible reasoning to solve practical problems related to other school disciplines
3	Students’ orientation in the modern world	Intention to apply mathematical tools for association to their environment	Awareness of importance of mathematical knowledge and skills for further education and profession	Understanding of the features of mathematical models and their use for practical activity	The development of research with the involvement of the appropriate mathematical tools

This table demonstrates the implementation of the motivational role of practice and instructional techniques related to students’ activity. The majority of the characteristics reflected in Table I are not tied to a particular stage of the teaching process. Mathematical knowledge and skills are enriched when students move to the next stage, which reinforces the stability and depth of their motivation.

5. Conclusion

The study of the nature of mathematical activity identifies a number of key factors which help to creatively regulate and stimulate motivational processes. These include capacious and precise ‘linguistic’ means of expressing mathematical regularities, the need for their justification and the development of a mathematical apparatus that enables a solution to any given problem of an applied nature. These factors can be described in hierarchical sequence [17, 18].

The initial link in this sequence is the practical need for solving specific pressing problems from the field of real human activity by the application of tailor made mathematical activity. In particular, it is expressed in the fact that any given practical task can stimulate the development of certain mathematical methods which in turn facilitate useful generalizations that would later extend those methods to a whole range of practical problems. This can itself become the starting point for relatively long-term mathematical research and open up the possibility of applying the developed mathematical theories to as yet unsolved practical problems. It can also help specify the prerequisites for the application of the developed mathematical tools to future stages of the development of science.

All these aspects should be taken into account when studying the school based mathematics curriculum. They offer a rich set of motivational opportunities. The particular motivational mechanisms which are applied will always initially be mindful of age range. In the initial stage of teaching mathematics, practical activity is basically a directly stimulating function in which the main role belongs to observation and experiment (real tasks for computing, measuring, plotting, constructing, etc.).

Motivational potential is then enhanced by demonstrating how a specific method for solving a specific problem can be used as the launching pad for the further development of the problem and for proving a theorem. The intention in so doing is to correlate this activity with the students’ previous real life experience. Later, the motivational role of practice is realized through the recognition of the role of the studied mathematical content in the deployment of related courses and also through consideration of the history of the emergence and evolution of scientific concepts and methods. Further it develops understanding of the various elements of mathematical modeling of real states and processes which underpin the mastery of applied mathematical ideology. Textual tasks are at the core of the mechanism for such an implementation. All this continues at the most senior levels, but this is now combined with a growing awareness of ecological orientation – of the importance of the mathematic repertoire for general involvement in the world and in particular for the successful implementation of future professional activity. This function can be performed using real-world applications using a sufficiently serious mathematical tools.

The implementation of these mechanisms, reflecting the specifics of the implementation of the motivational role of practice in relation to mathematics, requires careful and precise correlation with each student’s educational activity. The relevant material is presented in detail in our textbooks and articles.

1.  R. Courant, H. Robbins, What is Mathematics? An elementary approach to ideas and methods: London, Oxford University Press Incorporated, 1996.
2.  M. Kline, Mathematics. The Loss of Certainty: New York, Oxford University Press, 1980.
3.  M. Rodionov, The Formation and development of students motivation: Saransk, MGPI, 2012.
4.  M. Rodionov, Z Dedovets, “ Practical Problems as Tools for the Development of Secondary School Students’ Motivation to Learn Mathematics” in 19th International Conference on Computer Supported Education and Information Technology, New-Your, USA, 2017 https://waset.org/publications/10008026/
5.  G. Polya, Mathematics and Plausible Reasoning: Induction and analogy in mathematics: Princeton, New Jersey: Princeton University Press, 1954.
6.  L.C. Karpinsky, H. Y. Benedict, J. W. Calhoun, Unified Mathematics: Boston-New York-Chicago, D. C. HEATH & CO., 1918.
7.  T. Larkin, D. Budny, “Learning styles in the classroom: approaches to enhance student motivation and learning” in 6th International Conference on Information Technology Based Higher Education and Training, Santo Domingo, Venezuela, 2005. https://ieeexplore.ieee.org/document/1560310/
8.  M. B. Balk, V.A. Petrov, “About the mathematization of problems arising in practice” Mathematics at school, 3, 55-57, 1986.
9.  N. A. Tereshin, Applied orientation of school mathematics: M. Education, 1990.
10.  A. Ovezov, “Applying mathematical reasoning” Mathematics at school, 4, 45–52, 1998.
11.  A. D. Myshkis, M. M. Shamsutdinov, “Methods of applied mathematics” Mathematics at school, 2, 12-14.
12.  I. I. Blekhman, Mechanics and Applied Mathematics. Logic and applications of mathematics: M. Science, 1983.
13.  P. T. Apanasov, N. P. Apanasov, Collection of math problems with practical content: M. Education, 1987.
14.  H. Freudenthal, Mathematics as an Educational Task: Dordrecht-Holland, D. Reidel Publishing Company, 1973.
15.  W. Sawyer, Prelude to Mathematics: M. Education, 1972.
16.  I. Stewart, Concepts of Modern Mathematics: New York, Dover Publications, 1995.
17.  A. N. Tikhonov, D. P. Kostomarov, Stories about applied mathematics: M. Science, 1991.
18.  G. M. Wozniak, “The motivation problem in education” Mathematics at school, (2), 9-11, 1990.

(Click Here)

(Click Here)