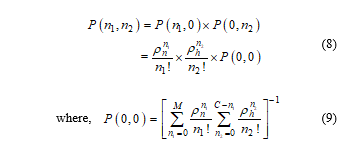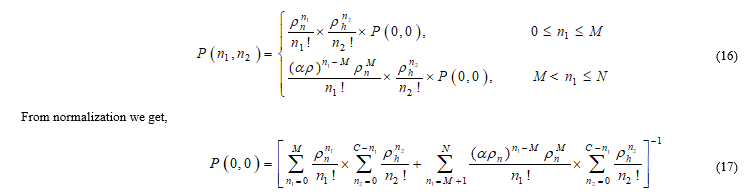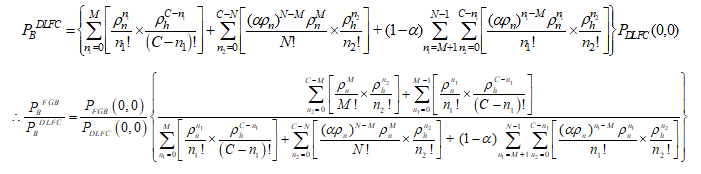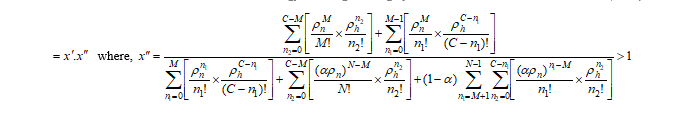1. Introduction

With the blessing of the communication system, the modern civilization has achieved an unbelievable pace. Because of the revolution of communication system, the whole world is becoming closer day by day. In this modern era, there is a lot of communicating ways like telephone, fax, television, radio, email, mobile phone, video conferencing, etc. those can be broadly classified into two categories – Wired and Wireless. Nowadays, the cellular communication technique becomes the most preferred compared to the other communicating ways of the wireless communication systems because of its vigorous number of facilities like mobility, intelligent network system, and various services in single network, convergent capability of different network system etc. That is why the demand of cellular network is increasing tremendously which leads to notable curiosity and improvement in the arena of wireless infrastructures [1].

The area covered by the cellular network is allocated into different precise sections which are termed as cells. When a mobile user exceeds the boundary of the cell or the wireless link quality becomes unacceptable, usually, the procedures of the handover call are originated [2]. Therefore, there are two categories of calls those can be commenced in a cell. One is a new call and another is a handover call which comes from the neighboring cell. Recently, a significant propensity in scheming the wireless cellular network is reducing the area of cell size and increasing the mobility of the users. This designing proposition results in frequent call handovers in wireless communication systems [3]. The probability of blocking a new call request by the network due to the lack of resources is called new call blocking probability (NCBP). On the other hand, an accepted enduring call is being terminated due to the lack of recourses is often termed as a handover call dropping probability (HCDP). In addition to that, NCBP and HCDP are two important qualities of service (QoS) parameters in single service cellular networks. According to the survey [4], the HCDP of a cellular network must be less than 2%. That’s why for giving the priority to the handover call, an intelligent network should be designed. A call admission control (CAC) is such an intelligent call management scheme that purposes to uphold the delivered QoS to the different calls of the network at the target level by off-putting the number of continuing calls in the system [5-6].

A number of CAC schemes have been proposed by considering different aspects. Among them, providing the priority to the handover calls several CAC schemes have been suggested in [1], [7]-[20]. Most of these propositions [1], [7-13] considered identical channel holding time regarding both the new and handover calls those specify one-dimensional Markov queue process.  On the other hand, the research works proposed in [14-20] have been claimed that this one-dimensional queue method is not accurate and therefore they proposed different channel holding time approaches which are more suitable to evaluate the QoS of a CAC scheme. It is obligatory to reserve a few channels devoted for the exceptional type of calls like handover call for providing the priority. Since the bandwidth of the cellular network is inadequate, the proper utilization of the channels (or bandwidth) become challenging due to the channel reservation. On the other hand, the non-priority scheme offers maximum utilization of the radio resources but this scheme is completely unable to guarantee the gratified level of QoS. Therefore, there is always a tradeoff relationship between QoS and channel reservation.

Based on several original CAC schemes, some researchers suggested QoS optimization methods in several approaches as thinning scheme I [13], thinning schemes II and new call bounding (NCB) schemes [21], new thinning scheme [21], [22], cutoff priority scheme [20], [23], etc. The NCB and thinning II schemes use the method of restriction over the acceptance of the new calls. The thinning scheme I is designed based on the defined the edge value of occupied channels as well as thinning scheme II works based on the probability of the new call acceptance at different numbers of new calls existed in the cell of the network. The new thinning scheme is another CAC policy that offers to fractionise the acceptance of the new call on only one channel which is basically designed considering the idea of limited fractional channel scheme (LFC) [13] in two dimensional Markov environments. The authors of the LFC scheme claimed that this CAC scheme is optimum with respect to thinning scheme I. On this contrary, the new thinning scheme is optimum with respect to NCB and thinning scheme II. The authors of the research works proposed in [13], [21-22] did not explicate the effects of fractionizing more than one channel. Although for the first time the concerning effect is interpreted in the method named uniform fractional band (UFB) scheme [24], the performance measurement is performed by considering one dimensional Markov process. It is already clarified that among the aforementioned CAC schemes, the LFC and new thinning schemes are optimum CAC schemes in one dimensional and two dimensional Markov process, respectively. Nevertheless, both research works also did not state the effect on QoS parameters in case of fractionizing more than one channel. Therefore, the consequential demand is to determine the effects of fractionizing more than one channel under two dimensional Markov process. Elsewhere, the mathematical model of fractionizing more than one channel under two dimensional Markov process is quite complex because of its curse of dimensionality [25].

Considering the previous scopes, this research work proposes a new CAC policy considering two dimensional Markov process based statistical model entitled by defined limited fractional channel (DLFC) scheme. It is also mentionable that this DLFC scheme was primarily proposed by our conference paper in [26] but the detail performance and mathematical details have been presented in this work.

This paper contributes in some specific points those can be mentioned as: (i) In UFB scheme NCBP was reduced where HCDP remained constant. But in DLFC scheme the HCDP has been reduced where NCBP is often constant. In this case, it is analyzed that the QoS in the DLFC scheme is better than that of the UFB scheme. (ii) For the different number of fractional channel, both the HCDP and NCBP have been analyzed and graphical and tabular presentations have been presented in the DLFC scheme which wasn’t analyzed in the UFB scheme. (iii) HCDP and NCBP have been examined and presentations regarding graphical and tabular have been presented in DLFC scheme for different values of acceptance factor. (iv) HCDP and NCBP have been also studied for LFC and new thinning schemes and compared with the DLFC scheme. From the analysis, it is shown that the QoS of the proposed DLFC scheme is better than the conventional schemes.

2. Parameters Portrayal

2.1.  Call Admission Control

Call admission control or CAC is basically an algorithm that regulates the traffic volume in cellular networks. CAC can also be used to maintain QoS by providing priority to a specific class of traffic. Generally, there are two kinds of CAC schemes, in broader senses and those are static CAC and dynamic CAC [7]. In this paper, we are concerned about the Static CAC scheme for the augmentation of the QoS. Static CAC schemes use the avowed traffic profile with no effort to estimate the authentic traffic. A proper CAC scheme depends on some parameters. Most significant parameters are: call holding time, cell dwell time, average call holding time, call arrival rate, call termination rate, and handover probability

• Call Holding Time: The call holding time means the call length in second from the initiation to termination of the call. The call may either stays in the cell or be handed over to another cell during this time. Generally, the parameter 1/μ is used to define the call holding time, T_n in units of seconds to designate the average call length of time. Here, μ denotes the average channel departure rate. It is often assumed that the average call length time is a random quantity with exponential distribution.
• Cell Dwell Time: In a modern high-speed communication system, it is always considered that the mobile users randomly move from one cell to another. Therefore, call handover is a very common case in the mobile cellular network. The time T_h what actually spent in a specific cell only before handed over the call is known as the cell dwell time. It means the average duration the calls dwell in the cell. The average dwell time is presented as 1/η, where η denotes the call termination rate in that cell only.
• Average Call Holding Time: The average holding time is the average time occupied for an operating network to response a call or the time a mobile user waits in the queue for the response. If the average dwell time is 1/η and the average call length is 1/μ, then the average call holding time, 1/μ_c is found as,

• Call Arrival Rate: At which rate, the new calls and the handed over calls from the neighbor cell arrive in a cell are called the call arrival rate and often denoted by the symbol . In a mobile cellular network, two kinds of calls are generated- new calls and handover calls. The new call arrival rate is denoted by  and handover call arrival rate is denoted by .
• Call Termination Rate: The amount of terminating calls in a cell in unit time is called the call termination rate, . The new call termination rate is denoted by and for the handover call, it is denoted by . In practice, these parameters are not equal. If these parameters are considered as equal the system can be modeled by one dimensional Markov process. Whereas, on the consideration of requires two dimensional Markov process.
• Handover Probability: The call handover probability, P_h is the probability of a call being handed over from one cell to another. Generally, in the case of a handover call, the call holding time T_n is greater than the call dwell time, T_h. Since both T_n(1/μ) and T_h(1/η) are considered as exponentially distributed according to the call arrival characteristics. The handover probability, P_h of a call in a particular time can be calculated as,

2.2.  The significance of CAC and Resource Reservation

CAC and resource reservation (RR) for mobile communication are of the most important issues that guarantee system efficiency and QoS required for different services in a very scarce resource as the radio spectrum. As forced call termination due to the handover call dropping are generally less desirable than blocking a new one, handover calls should have a higher priority than new calls [26].

2.3.  Mathematical Modeling of CAC schemes

Mathematical model subjected to a CAC scheme can help to indicate the performance of the network. This modeling is based on some probability theory due to its random nature. Therefore, a basic discussion over CAC scheme modeling with possible terminology have been explored and explained, gradually.

• Queuing Theory: The queuing theory is a mathematical approach of waiting in lines or queues. In queuing theory a model is constructed so that queue lengths and waiting time can be predicted. Networks of queues are systems in which a number of queues are connected by customer routing. When a customer is serviced at one node it can join another node and queue for service, or leave the network. For a network of m, the state of the system can be described by an m–dimensional vector where x_i represents the number of customers at each node. Queuing theory maintains the birth and death process.
• Markov Process: Markov process is a statistical method which is used to predict the forthcoming behavior of a variable or system whose existing behavior does not depend on its behavior at any time in the past. In other words, this procedure works with random variables. Basically, a Markov process works with a sequence of random variables suppose with the Markov property, such as the current, future, and past states are independent. Formally,

If these two conditional probabilities are properly defined, i.e. if,

The probable values of X_i construct a countable set, S which is known as the state space of the chain. This Markov chain may be either single dimensional or multidimensional.

• Multidimensional Markov Model: Suppose that, we have s categorical sequences and each sequence has m possible states in M. In addition, let x_n^(k) be the state probability distribution vector of the j^th sequence at time n. Therefore, if the probability of founding the j^th sequence in state j is one at time n, the following relation can be considered.

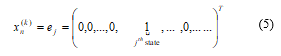Furthermore, it can also be assumed that the following relationship exists among the sequences.

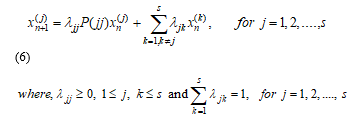This mathematical relationship basically represents that the state probability distribution of the j^th chain at the time (n +1) and it totally depends on the weighted average of P(jj)x_n^(j) and the probability distribution of the state at the other chains at time n. Here P(jj) denotes the one-step transition probability matrix of the j^th Sequence. We can write the system in matrix form as,

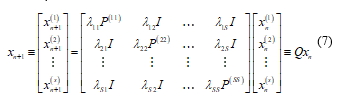For the relation (7), the following proposition can be considered as a generalized version of the Perron Frobenius theorem [27].

From the above theoretical view of multidimensional Markov chain model, we get the concept of using two dimensional Markov chain model for the purpose of call admission control in a wireless network. It provides desired QoS for handover calls and guarantees that the QoS of new calls still meets the requirements. When congestion occurs, we may lose both of these purposes. The average service rate of the new call and handover call  and  are not the same. Different CAC schemes are designed under 2D Markov process. Among them cut off priority and limited fractional channel CAC schemes are most common those have been discussed here. These methods have also been widely examined to compare with our proposed scheme.

• Cut off Priority CAC Scheme: The transition rate diagram of two dimensional Markov chain model for the cutoff priority CAC scheme [20], [23] is given in Figure 1. In this figure, denotes the number of new calls, denotes the number of handover calls and M is the defined threshold for new call acceptance. New traffic load and handover traffic load are defined as and  where  and  are the new call and handover call arrival rate respectively and     are the average termination rate for new and handover calls, respectively. If  denotes the steady state probability, then from the balance equation we have [21],

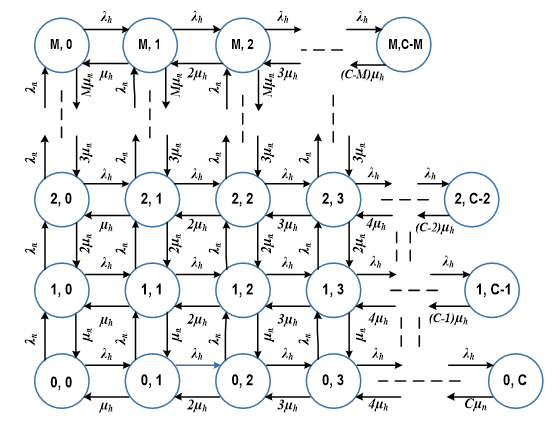Figure 1: Transition rate diagram based on two-dimensional Markov model obeying the Cut off Priority scheme of CAC

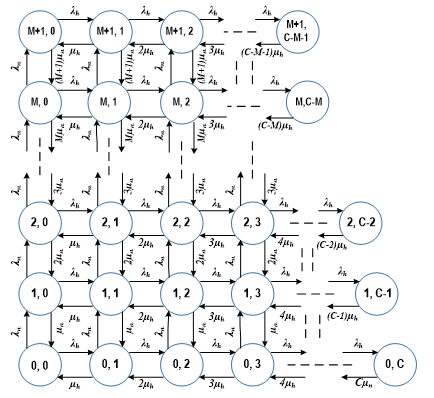Figure 2: Transition rate diagram of LFC scheme under two dimensional Markov chain model

The new NCBP, P_B and HCDP, P_D can be derived from the above equation as the relation given below:

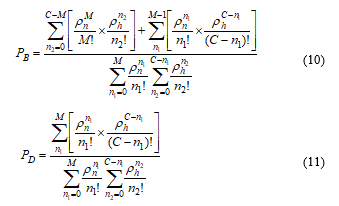• Limited Fractional Channel (LFC) Scheme: This scheme was first introduced by R. Ramjee in [13] as optimal CAC. But he assumed and  equal as it was designed under the one-dimensional Markov process. In practical case   [26-28]. Then LFC scheme has been discussed under two dimensional Markov process in [22] which was named as new thinning scheme. In this paper, one channel was fractionally used for accepting new calls with an acceptance factor, . But the authors did not discuss the situation while more than one fractional channel are considered. The transition diagram of the LFC scheme under two dimensional Markov process has been given in Figure 2.

From the Figure 2, the mathematical expressions can be derived. If  denotes the steady state probability when there are new calls and  handover calls in the cell, then from balance equation we have,

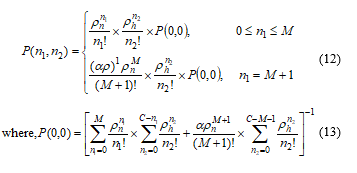The NCBP and HCDP of the new thinning scheme are estimated by the mathematical relation given by (14) and (15), respectively.

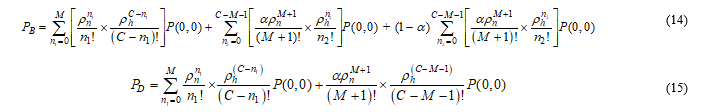
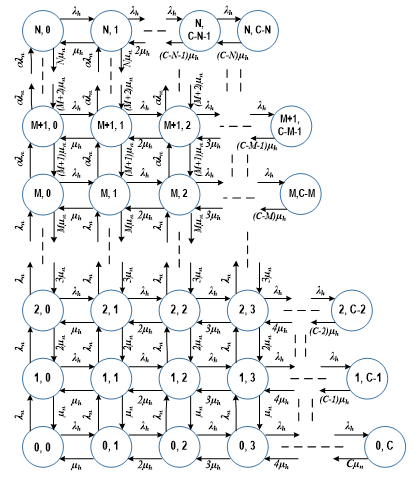Figure 3: Transition rate diagram of proposed DLFC scheme of CAC under two dimensional Markov chain model

3. Proposed DLFC

3.1.  Mathematical Modeling of the Proposed DLFC Method

This CAC scheme is proposed under two-dimensional Markov process where, . For increasing channel utilization fractional channel scheme is used and the number of fractional channels is considered more than one. That’s why this scheme is named Defined Limited Fractional Channel scheme (DLFC). After occupying the M channels, the additional new calls will be admitted with a certain probability “α”. Therefore, the new calls will be opposed with probability 1-α in those states. Finally, only handover calls will be acceptable from M+N to C. If all channels are busy, handover calls will be dropped. The proposed scheme with its transition properties is illustrated in Figure 3. In this scheme, we have assumed a different channel holding time for each type of calls. Thus, the different channel holding time ( ) offers the state transition rate diagram to be two dimensional. In Figure 3, and  denotes states new calls and handover calls, respectively. The and  indicates the new call traffic load and handover call traffic load, respectively. For call admission controlling of DLFC scheme, a flowchart is given below in Figure 4. From this figure, it can be explained that at first, the system will analyze the call type either handover or a new call. If the call is a handover call then the availability of the channel less than C will be checked. If yes then the call will be accepted if not then it will be blocked. If the call is a new call then the availability of channel less than M will be checked. If yes then the call will be accepted and if not then the availability of channel M to N-1 will be checked for their availability. For being available the call will be accepted with predefined acceptance factor α. If not then it will be blocked.

From the Figures 3 and 4, mathematical terminologies of the DLFC scheme have been derived. If  denotes the steady state probability considering that there present  new calls and   handover calls in the cell. From the balance equation we have,

where, M and N denote the threshold channel and priority to the channel, respectively.

The NCBP and HCDP of the DLFC scheme can be found as (18) and (19), respectively.

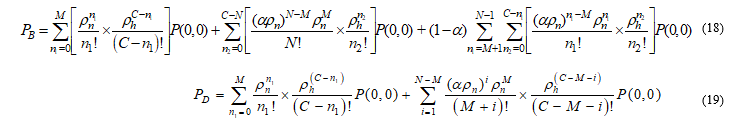when                        ® (Simple guard channel (GC))

                                  ®  (LFC) [13], [21]

                                  ®  (Defined limited fractional channel) again    GC;

                                ; These channels show the non-priority characteristics.

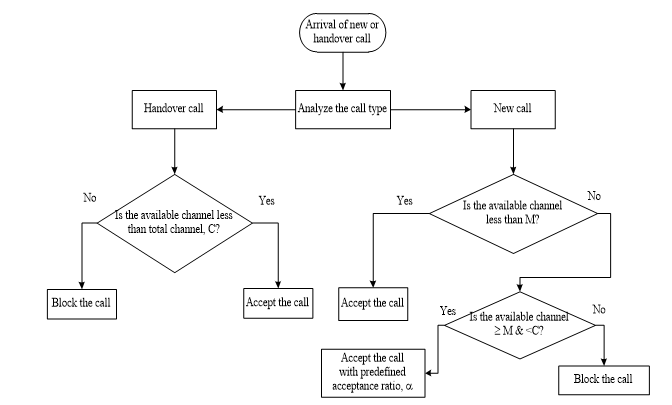Figure 4: The conditional steps of call admission according to the DLFC scheme

3.2.  Numerical Evidence of Optimality for DLFC scheme

For designing a CAC scheme it is important to ensure QoS. In [13] it is stated that cut off priority scheme is the optimal CAC scheme. But DLFC is more optimal than cut off priority scheme because the HCDP is less than cut off priority scheme in DLFC where NCBP is almost constant. As  and are not linearly related [1] it is too complicated to prove the optimality for DLFC. Here, numerically we have proven the optimality of the NCBP and HCDP based estimation by the proposed DLFC scheme individually.

Numerical Evidence of Optimality for NCBP (P_B): Let us consider, total channel=C and guard channel= M, for Fixed Guard Band (FGB) or cut off priority scheme. From the relation (9) we get,

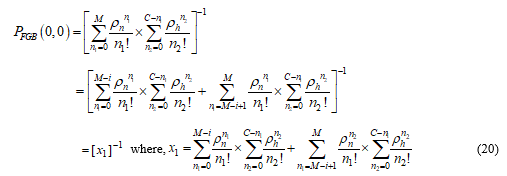Again acceptance factor, 0<α<1; Fractional priority to N=M and number of fractional channel = N-M= i; for proposed DLFC scheme. From the relation (17) we get,

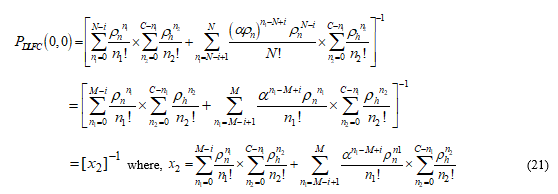Now for blocking probabilities from equations (10) and (20), we can estimate NCBP for FGB scheme as,

Handover dropping probability for DLFC scheme,

                        where,

because, and , therefore it can be said that . From this relation, it is proved that NCBP is almost same in FGB and DLFC. A truth table for this evidence is given in Table 1 where M=80; C=100; i=1 and α=0.5.

Table 1: Truth table of optimality test for DLFC regarding NCBP

Serial No	Erlang	x′	x″	X=x′*x″	PBDLFC-PBFGB
1	72	0.95396	1.125123788	1.07	0.002533046
2	108	0.814726	1.242736145	1.01	0.003510861
3	144	0.739994	1.358456043	1.01	0.002376509
4	180	0.693542	1.446178112	1.00	0.00167154
5	216	0.662022	1.51347319	1.00	0.001234904
6	252	0.639281	1.566425511	1.00	0.000948721
7	288	0.622116	1.609086009	1.00	0.000751506
8	324	0.608707	1.644154299	1.00	0.00060996
9	360	0.597946	1.673476122	1.00	0.000504963

 Numerical Evidence of Optimality for DLFC by HCDP (P_D): Similarly for HCDP of FGB scheme from equation (11) we get,

HCDP of DLFC from equation (19) we get,

 Finally, it is also proved that HCDP of DLFC scheme is less than that of FGB. A truth table for this evidence is given in Table 2 where M=80; C=100; i=1 and α=0.5. From the table, it is found that the previously claimed condition has been successfully achieved. The value of X corresponding to every value of the Erlang* is greater than 1. This condition is hypothesized by the proved relation given in (23).

[*An Erlang is a unit to measure the traffic load or total traffic volume of one hour in telecommunication systems.  Therefore, Erlang = number of calls × duration]

Table 2: Truth table of optimality for DLFC by HCDP

Serial No	Erlang	x′	x‴	X
1	36	1	1.256047896	1.26
2	72	0.95396	1.343211738	1.28
3	108	0.814726	1.524809854	1.24
4	144	0.739994	1.614197079	1.19
5	180	0.693542	1.675859871	1.16
6	216	0.662022	1.720978322	1.14
7	252	0.639281	1.755288598	1.12
8	288	0.622116	1.782196438	1.11
9	324	0.608707	1.803834919	1.10
10	360	0.597946	1.821599044	1.09

4. Results and Discussions

In this section, the simulation results have been presented for the assessment of the proposed DLFC scheme with the other conventional schemes under 2D Markov process based on statistical modeling. These results show how much deviation may take place for applying the proposed scheme with respect to the other traditional CAC schemes. On the other hand, the various features of the proposed scheme have been also described gradually. First of all, investigations of all the CAC schemes were carried out considering some basic assumptions. For simulating the proposed methodology regarding CAC scheme designing in 2D Markov process, we assumed some parameters as the numerical values represented in Table 3. These parameters were always considered in a similar manner for all the performance analysis of the conventional schemes as well as the proposed DLFC scheme.

Table 3: Basic assumptions of some parameters

Parameters	Nomenclature	Values
Total Channel	C	100
Guard Channel	M	80
Fractional Guard Channel	M	75~79
Fractional Priority Channel	N	80
Traffic Load (New Call)		0~360
New Call Termination Rate		1/120
Handover Call Termination Rate		1/60
Acceptance Factor	α	0~1

In numerical results, the new NCBP’s and handover HCDP’s of the DLFC cut off a priority, and LFC schemes were examined in two dimensional Markov process. The performances of all the schemes were analyzed with different conditions like fractional channel numbers and different values of acceptance factor. According to the basic assumption of the system parameters, all the mathematical calculation has been performed in MATLAB 2012b. The two dimensional Markov model was prepared by MATLAB code and based on this model all the traffic load was analyzed to estimate the performances of the different schemes.

The HCDP of the wireless network under the conditions of given parameters of Table 3 regarding different traffic load were analyzed and compared the performances. Figure 5 presents such a comparison among the various popular CAC schemes as well as the proposed scheme regarding their HCDP performances. This figure shows that the proposed scheme confirms the lowest HCDP than the others and the highest HCDP occurs in case of the cut off priority scheme. DLFC scheme has a lower HCDP than LFC and cut off priority schemes.

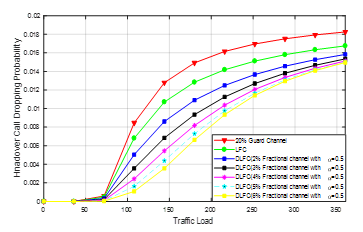Figure 5: Handover call dropping probabilities for the different number of fractional channel for DLFC with Cut off Priority and LFC scheme

It is also observed that by increasing the number of the fractional channels the HCDP can be reduced. But there is a limit to increasing the number of fractional channels. After increasing the value to the limit the HCDP remain almost the same. In Figure 5, it was found that the values of HCDP for 5% and 6% fractional channels of the assumption are almost the same for the high traffic load.

The NCBP of the cutoff priority scheme, LFC, and proposed DLFC schemes have been calculated and presented to show the comparison among their performances and presented in Figure 6. Here it is observed that the NCBP are almost same for cut off priority, LFC, and proposed DLFC scheme at higher traffic load which is our real concern. DLFC scheme has a marginally higher NCBP than LFC and cut off priority schemes at the lower new call arrival rate but same performance in the higher new call arrival rate. In this analysis, the basic assumptions were the same as in Figure 5.

We assumed that all the parameters became same except acceptance factor and for different acceptance factors the HCDP have been calculated. The results concerning this consideration have been presented in Figure 7. The value of α must be . In this analysis acceptance factor is assumed as α=0.2, 0.3, 0.5, 0.75 & 0.9. It is observed that with the increment of acceptance factor the HCDP increased. The less the acceptance factor is presented in the system, we found the less HCDP. Figure 7 presents the HCDP’s of DLFC scheme for the different values of α. Here, one thing can be approached that if we choose the acceptance factor to be 0.5 the dropping probability remains at a satisfactory level. For the value of acceptance factor 0.75 and 0.9, the HCDP increases drastically, which is a threat for the QoS.

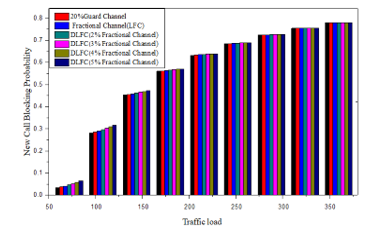Figure 6: New Call Blocking Probabilities for different no of the fractional channel for DLFC with cut off priority and LFC scheme

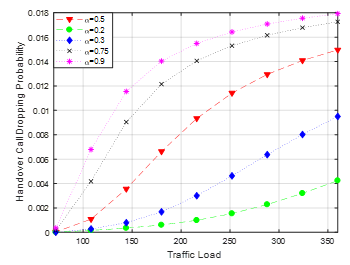Figure 7: Handover Call Dropping Probabilities for different values of acceptance factor for DLFC

In addition to that, with the similar conditioning, the performances regarding NCBP of the proposed DLFC scheme have been also assessed. The results we found have been presented in Figure 8. From this figure, we can perceive that there are some effects of the acceptance factor at the lower traffic load. On the other hand, at the higher traffic load, this effect does not carry any significance which is very concerning the issue of the proposed scheme.

This scheme offers a system where the HCDP will be decreased without affecting the NCPB which has been achieved by the results given in Figure 8. Therefore, the proposed scheme improves the QoS of the wireless network where we are concerned about the HCDP at the very high traffic load. So, the results clarify that the DLFC scheme reduces HCDP without hampering the performance of the system’s NCPB. The additional benefit of the proposed scheme is the regulating properties of the acceptance factor. To achieve a certain level of QoS, we can select our acceptance factor to maintain the HCDP and NCBP at our satisfactory level with respect to the load. In addition, it can be chosen according to traffic load arrived in the cellular network.

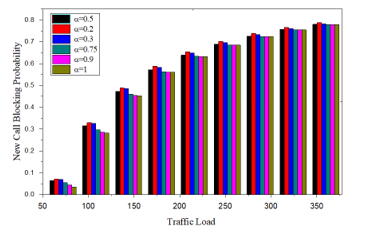Figure 8: New Call Blocking Probabilities for different values of acceptance factor for DLFC

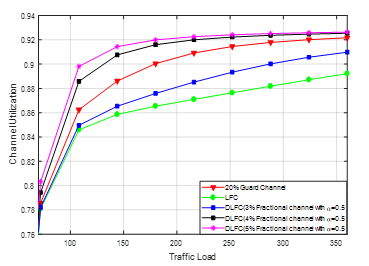Figure 9: The performance of channel utilization by the DLFC, cut off priority, and LFC scheme regarding different traffic load

Extra concerning issue for the QoS associated with the CAC policy is channel utilization. In Figure 9, the channel utilization performance of the proposed DLFC scheme has been presented comparing with the conventional cut off priority scheme and LFC scheme. Channel utilization of all the schemes discussed here remains the same for almost all the cases. Although the cut-off priority scheme shows the highest performance of channel utilization, the proposed DLFC scheme has also almost similar channel utilization performance by tuning the acceptance factor.

In Figure 10, channel utilization of DLFC scheme has been shown under various values of acceptance factor α. This acceptance factor has a nice tuning effect on the performance of the channel utilization. Therefore, it is easier to attain the required system’s channel utilization performance by the proper selection of the call acceptance factor. It should be mentioned here that, with the help of reducing the NCBP we can increase the channel utilization but in this case, it will be difficult to maintain the QoS. To maintain the importance of handover call we should take into account not only the blocking probability but also the channel utilization as well. To optimize the system performance, we can regulate the acceptance factor through the DLFC scheme.

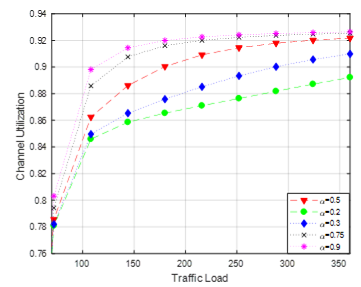Figure 10: The performance of channel utilization by the DLFC, cut off priority, and LFC schemes regarding different acceptance factors

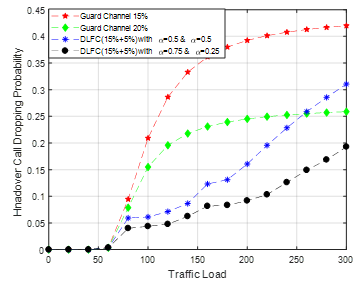Figure 11: The performance of the DLFC scheme while it is used as a hybrid approach with compared to the guard channel scheme.

This DLFC scheme has another beautiful feature which is its utility of hybrid approach of call acceptance rate. If we consider 15% guard channel and 20% guard channel in cutoff priority scheme, there we find a major difference in handover call dropping probability. On the other hand, we can solve this problem with the proposed DLFC scheme. We can reduce the handover call dropping probability to a satisfactory level by using the utility of the regulation of the acceptance factor. Such a result has been given in Figure 11. Here, we can observe that if we divide the 20% guard channel as 15%+5% and choose different acceptance factors for two different divided channel groups, the HCDP reduces significantly. Here, acceptance factor 0.75 has been chosen for the 1^st 15% guard channel and for the rest 5%, the acceptance factor has been chosen 0.25. For both (15% and 5%) guard channel the acceptance factor 0.5 has been used in Figure 11 to show the reference performance of the proposed DLCF scheme.

5. Conclusions

The radio resource is limited to a system. For this reason, providing a priority to one class in its call admission is a cause to increase the call blocking probabilities of other classes. Since handover call dropping is practically much more annoying than the new call blocking, in this research paper, a new call admission control scheme has been proposed which is termed as a defined limited fractional channel or DLFC scheme. The NCBP and HCDP of the proposed scheme have been estimated from the model designed MATLAB 2012b and also compared to the existing methods under two dimensional Markov process based statistical modeling. In this case, it has been observed that the HCDP is decreased where NCBP is almost the same with respect to the cut off priority scheme and LFC schemes. It has been perceived from the simulation results that the performance of the DLFC depends upon the number of fractional channels and the values of the acceptance factor.  So, it becomes a major concern to choose the number of fractional channels and the value of the acceptance factor.

This DLFC scheme has been investigated in a two-dimensional Markov process. There is scope to analyze this idea under multidimensional Markov process for multi-service wireless network and to find out the effect on performances of this scheme and its curse of dimensionality.

Conflict of Interest

The authors of this paper declare that there is no conflict of interest and commercial engagement with other parties regarding this research work.

Acknowledgment

All authors of this paper would like to thank Prof. Dr. Mostafa Zaman Chowdhury, Dept. of EEE, Khulna University of Engineering & Technology (KUET), for his valuable guidance from the beginning of this research work.

1.  M. A. Rahman, M. A. Hossain, S. Ahmed, and M. Z. Chowdhury, “A New guard-band call admission control policy based on acceptance factor for wireless cellular networks,” International Conference on Informatics, Electronics & Vision (ICIEV), pp. 1-5, May 2014. DOI: 10.1109/ICIEV.2014.6850803.
2.  A. Sgora, Vergados, and D. Dimitrios, “Handover prioritization and decision schemes in wireless cellular networks: A survey,” IEEE Communications Surveys and Tutorials, vol. 11, no. 4, pp. 57-77, December 2009. DOI: 10.1109/SURV.2009.090405.
3.  M. Z. Chowdhury, Y. Min Jang, and Z. J. Haas, “Call admission control based on adaptive bandwidth allocation for wireless networks,” Journal of Communications and Networks, vol. 15, no. 1, pp. 15-24, February 2013. DOI: 10.1109/JCN.2013.000005.
4.  Y. Fang, “Modelling and performance analysis for wireless mobile networks: A new analytical approach,” IEEE/ACM Transaction on Networking, vol. 13, no. 5, pp. 989-1002, October 2005. DOI: 10.1109/TNET.2005.857119.
5.  M. Z. Chowdhury, M. S. Uddin, and Y. M. Jang, “Dynamic channel allocation for class-based QoS provisioning and call admission in visible light communication,” Arabian Journal for Science and Engineering, vol. 39, no. 2, pp. 1007-1016, February 2014. DOI: 10.1007/s13369-013-0680-4.
6.  M. Mamman, Z. M. Hanapi, A. Abdullah and A. Muhammed, “An adaptive call admission control with bandwidth reservation for downlink LTE networks,” IEEE Access, vol. 5, pp. 10986-10994, 2017.
   DOI: 10.1109/ACCESS.2017.2713451
7.  M. Schneps-Schneppe and V. B. Iversen, “Call Admission Control in Cellular Networks,” Mobile Networks, Chap. 6, pp. 111-136, InTech Publisher, 2012. DOI: 10.5772/35866.
8.  M. Ghaderi and R. Boutaba, “Call admission control in mobile cellular networks: A comprehensive survey,” Wireless Communication and Mobile Computing, vol. 6, no.1, pp. 69-93, February 2006. DOI: 10.1002/wcm.246
9.  K. Bhoite and S. Gengaje, “Handoff Prioritize Call Admission Control Policy for Integrated Macrocell-Femtocell Network,” International Journal of Computer Applications, vol. 164, no. 2, pp. 21-26, April 2017. DOI: 10.5120/ijca2017913593.
10.  M. Jain and R. Mittal, “Adaptive call admission control and resource allocation in multiserver wireless/cellular network,” Journal of Industrial Engineering International, vol. 12, no. 80, pp. 71-80, November 2015. DOI: 10.1007/s40092-015-0129-3.
11.  H. Beigy and M.R. Meybody, “A new fractional channel policy,” Journal on High-Speed Networks, vol. 13, no. 1, pp. 22-36, 2004.
12.  J. L. V. Avila, A. Flipe, C. Perez, and L.O. Guerrero, “Performance analysis of fractional guard channel policies in mobile cellular networks,” IEEE Transactions on Wireless Communications, vol. 5, no. 2, pp. 301-305, February 2006. DOI: 10.1109/TWC.2006.1611053.
13.  R. Ramajee, R. Nagarajan, and D. Towsley, “On optimal call admission control in cellular networks,” Wireless Networks, vol. 3, pp. 29-41, 1997. DOI: 10.1109/INFCOM.1996.497876.
14.  M. B. A. Sadi and A. Nadia, “Call admission scheme for multidimensional traffic assuming finite handoff user,” Journal of Computer Networks and Communications, vol. 2017, Article ID 6101568, 5 pages, 2017. DOI:10.1155/2017/6101568.
15.  J. Hou and Y. Fang, “Mobility-based call admission control schemes for wireless mobile networks,” Wireless Communication and Mobile Computing, vol. 1, pp. 269-282, 2002. DOI: 10.1002/wcm.18.
16.  Y. Fang, “Thinning scheme for call admission control in wireless networks,” IEEE Transactions on Computers, vol. 52, no. 5, pp. 685-687, May 2003. DOI: 10.1109/TC.2003.1197135.
17.  J. L. V. Avila, A. Flipe, C. Perez, and L.O. Guerrero, “Performance analysis of fractional guard channel policies in mobile cellular networks,” IEEE Transactions on Wireless Communications, vol. 5, no. 2, pp. 301-305, February 2006. DOI: 10.1109/TWC.2006.1611053.
18.  X. Wang, P. Fan, and Y. Pan, “A more realistic thinning scheme for call admission control in multimedia wireless networks,” IEEE Transactions on Computers, vol. 57, no. 8, pp. 1143-1148, 2008. DOI: 10.1109/TC.2008.29.
19.  Y. Zhang and D. Liu, “An adaptive algorithm for call admission control in wireless networks,” IEEE Telecommunications Conference, vol. 10, no. 4, pp. 3628-3632, 2001. DOI: 10.1109/GLOCOM.2001.966358.
20.  Y. Fang and Y. Zhang, “Call admission control schemes and performance analysis in wireless mobile networks,” IEEE Transactions on Vehicular Technology, vol. 51, pp. 371-382, 2002. DOI: 10.1109/25.994812.
21.  Z. Firouzi and H. Beigy, “A new call admission control scheme based on new call bounding and thinning II schemes in cellular mobile networks,” IEEE Conference on Electro/Information Technology, vol. 09, pp. 40-45, June 2009. DOI: 10.1109/EIT.2009.5189581.
22.  Z. Firouzi and L. M. Far, “Defining interval for threshold in new thinning scheme,” Computer Science and Information Technology (ICCSIT), 2010 3rd IEEE International Conference, vol. 09, pp. 108 – 112, July 2010. DOI:
23.  D. Hong and S. S. Rappaport, “Traffic model and performance analysis for cellular mobile radio telephone systems with prioritized and no prioritized handover procedures,” IEEE Transaction on Vehicular Technology, vol. 35, no. 3, pp. 77-92, 1986. DOI: 10.1109/T-VT.1986.24076.
24.  M. A. Rahman, “QoS Provisioning Using Optimal Call Admission Control for Wireless Cellular Network,” M. Sc. Thesis Paper, KUET, 18 December 2014.
25.  E. Keogh and A. Mueen, “Encyclopedia of Machine Learning,” pp. 257-258, Springer 2010.
26.  M. A. Rahman, M. S. I. Sohag, and M. Z. Chowdhury, “A new fractional channel call admission control for handover priority,” International Conference on Informatics, Electronics and Vision (ICIEV), June 2016. DOI: 10.1109/ICIEV.2016.7759997.
27.  M. A. Rahman, A. S. M. Z. Shifat, and M. S. I. Sohag, “The effect of average channel holding time to estimate the QoS parameters of cellular network through guard channel scheme,” International Conference on Electrical Engineering and Information Communication Technology, May 2015. DOI: 10.1109/ICEEICT.2015.7307484.
28.  Y. Fang and I. Chlamtac, “Teletraffic analysis and mobility modeling for PCS networks,” IEEE Transaction on Communication, vol. 47, pp. 1062–1072, July 1999. DOI: 10.1109/26.774856.

(Click Here)

(Click Here)