1. Introduction

This paper is an extension of work originally presented in 2017 at the 5^th International Conference on Electrical Engineering-Boumerdes (ICEE-B) [1]. In the order to well detail, explain and develop the previous work presented in this latter conference. In nature, many processes can be modelled by a system of mathematical expressions [2]. Models usually contain some unknown parameters. In the object to find the values of these unknown parameters, some real measurements from the system are required, to be compared with the output of the models proposed through minimizing of some errors [3].  This problem is known as the parameters’ identification problem. In these systems, there is the process of modeling and after that, there is an identification process of the unknown parameters for the selected model [4]. In this order, we have used this discipline in a solar photovoltaic (PV) system, in order to identify the electrical parameters of the PV generators. These parameters are very necessary for simulating solar PV production’s behavior and therefore control it. As the high non-linearity found in PV cell’s models, we present in this work, the combination of two optimization algorithms for identifying the electrical PV generator’s unknown parameters from real experimental data. The PV parameters identification process for PV generators is shown in the Figure 1 below.

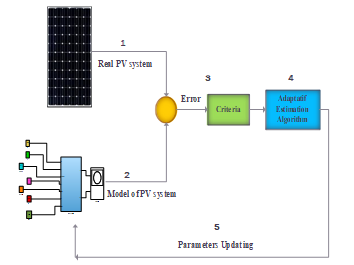Figure 1. Parameters Identification for PV generators.

The process of PV parameters identification is based on a prediction of the error between the real system and the theoretical model. This error is used with an appropriate algorithm that has to be modified at each iteration. In this order, the PV parameters are found through the main steps cited below, as illustrated in the above Figure 1:

1-      Obtain experimental data from a real PV installed system.

2-      Obtain data from a selected model representing a PV system.

3-      Minimize the error between the real data and the data of the selected model, using some criteria.

4-      Application of an appropriate identification adaptation algorithm.

5-      Update the PV parameters values that validate the final selected model representing the real system.

The organization of this paper is as follows: after having introduced the subject in this first section. The second section, gives a state of the art about the PV parameters identification existed methods. Then, the third section focuses on the major steps of PV parameters identification, with more details about each step. Herein, the use of the suggested combined optimization approaches. In the fourth section, a discussion is given concerning the obtained results, before some conclusions in the fifth section.

2. State of the art

In literature, many different methods exist to allow determining the electrical parameters values for the PV generators [5], [6]. Primary, scientific researchers have focuses on the parasitic resistances (series and shunt) determination [7], [8] by the cause of their major influences on the PV performances. Then, it was also observed some influences of all PV electrical parameters on the performances [9], which leads for doing a large number of studies for obtaining their accurate values. The elaborated studies are classified into several categories [5]. Certain methods are classified as theoretical methods such as analytic [10], numeric [11], [12]. Certain other methods are based on an experimental process and are known as identification methods [13], [14], [15]. All methods have their own advantage and inconvenient, to be chosen for using in such application, based on some criteria (complexity, convergence speed, precision …). In this work, we are going to well develop our identification approach.

3. Steps of Photovoltaic Parameters Identification

Parameters identification is an automatic technic, which consists to get a mathematical model, for certain system using some experimental measures. Therefore, the identification process is based on the development of a mathematical representation for a physical system by the use of experimental data [16] [17], through details explained in the main steps cited in the points below of Figure 2.

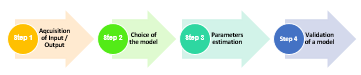Figure 2. Major steps of parameters identification in systems.

The above major steps of the identification process for PV generators, are well developed in the following points.

2.1.  First Step- “Acquiring of Real Data”

A description of our experimental work is giving in this subsection, for obtaining the real PV measured data information [18]. The data acquired issued from a PV system located at our laboratory, (Laboratoire de Dispositifs de Communication et de Conversion Photovoltaique, LDCCP). This acquisition work is schematized in Figure 3. The PV system contains a photovoltaic generator, which is composed of four PV panels associated in series, where each panel generate about 55 Watts of power. The measured parameters are the temperature, the solar irradiation, as well as the voltages and currents.  In order to collect data, the different components of the proposed PV measurement system are:

• A sensor of temperature ‘T’, the LM35.
• A sensor of solar irradiation ‘G’, the pyranometer.
• PV generator associated with the electronic load.

In order to draw the real current-voltage (I-V) curve of PV generators under real conditions, these generators are associated with an electronic load.  The process of information reception is made using a computer, which consists of the unit of treatment and control. In this context, we set up an experimental manipulation based on an Arduino-Uno card [19] that allows us the acquisition of data issued from a PV system installed in our laboratory. The transmission of these acquired data to a personal computer is ensured by a USB connection port (serial communication).

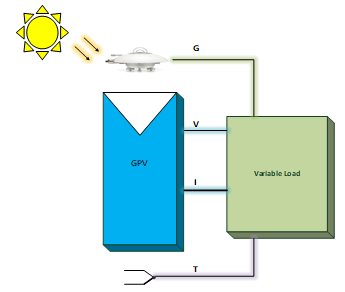Figure 3. Sensors and PV generator related to a variable load.

The proposed system consists of a set of sensors for measuring both meteorological (e.g. temperature, irradiation) and electrical parameters (photovoltaics voltage and current). The collected data are first conditioned using precision electronic circuits and then interfaced to a PC using a data-acquisition card (Arduino-Uno) [16]. The LABVIEW program is used to further process, display and store the collected data in the PC disk. We have conceived an electronic load based on a MOSFET transistor of power [20]. The variable load allows the measures of a couple of the current-voltage (I–V) along the curve. The obtained current–voltage characteristic (I–V) curve of our photovoltaic generator is illustrated in Figure 4, which was operated under the real environmental conditions (794.46W/m2, 30.85°C).

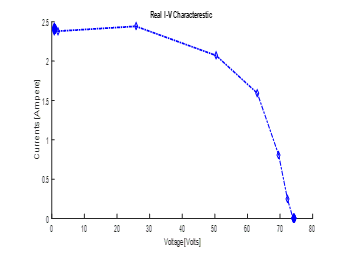Figure 4. The obtained Current–Voltage experimental curve at (794.46W/m2, 30.85°C) for the four series PV panels of type SM55.

The following Table I shows the PV manufacturer’s datasheet information of the SM55 PV panel used in this work [21].

Table 1. Specification of Siemens SM55 solar PV panel used, from datasheets under Standard-Test-Conditions : STC (T = 25 °C & G= 1 000 W/m²).

Parameters		Mono Crystalline Silicon
		Panel 21.7 3.45 17.4 3.15 55 36
Open Circuit Voltage (Volts) Short Circuit Current (Ampere) Maximum Power Voltage (Volts) Maximum Power Current (Ampere) Maximum Power Point (Watts) Number of cells in series	Voc Isc Vmpp Impp Pmpp Ns

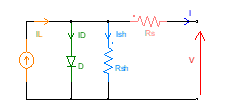Figure 5. Solar photovoltaic cell’s electrical equivalent circuit (The one diode model).

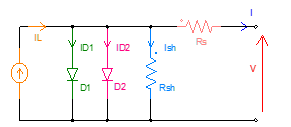Figure 6. Solar photovoltaic cell’s electrical equivalent circuit (The double diode model).

2.2.  Second Step- “Selection of the appropriate model”

An accurate mathematical model is an important tool for researchers. The one and double diode PV models, with 5 and 7 unknown parameters respectively, are represented as follow in Figure 5 and Figure 6 [22], [23], [24].

The mathematical equations related the Current-Voltage, (I-V) relationship of the electrical models are given below.

• The one diode model

 

The PV panel contains cells associated in series manners through the mathematical expression below.

Where:

(a)The one diode model

• I_L: Light current.
• I_ds: Diode saturation current.
• n: Diode ideality factor.
• R_s: Series resistance.
• R_sh: Shunt resistance.

 (b) The double diode model

• I_L: Light current.
• I_ds1: Diode saturation current.
• I_ds2: Reverse diode saturation current.
• n₁: Diode ideality factor.
• n₂: Second diode ideality factor.
• R_s: Series resistance.
• R_sh: Shunt resistance.

The PV Generator contains N_ms series branches and N_mp parallel branches.

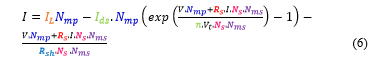N_s: Number of series cells. N_ms: Number of modules in series branches. N_mp: Number of modules in parallel branches.

The next Figure 7 shows the PV generator located at our laboratory.

Figure 7. Photovoltaic system mounted at our laboratory.

In our work (Figure 8), the PV generator has N_s of about 36, N_ms of about 4 and N_mp is 1.

2.3.  Third Step- “Parameters estimation”

In this step, the application of the chosen optimization algorithm to identify and obtain the optimal values of PV parameters. The idea is based on a prediction error between the output of the real PV process and the output predicted by the PV model [3], as explained before. This prediction error is used by a Parametric Adaptation Algorithm (A.A.P), which at each iteration will modify the parameters of the model in order to minimize the error, which will be detailed through the next subsections, as schematized in Figure 8.

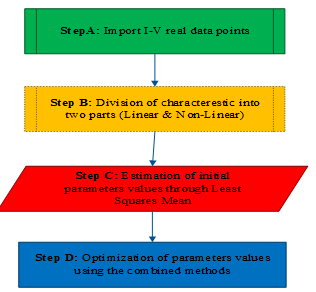Figure 8. Major steps to estimate, determine and optimize the PV parameters values.

These points will be well explained in the next subsections.

• The Least Squares Mean (LSM)

Different approaches allow the initial estimate of parameters values such as Least Squares (LS), Least Squares Mean (LSM), Recursive Least Squares (RLS), Recursive Extended Least Squares (RELS) and Newton stochastic (NS) [25]. In an optimization algorithm, the step of initialization of the unknown PV parameters is very necessary for converging to solution. In this regard, we have chosen for obtaining the initial values of our PV parameters the Least Squares Mean (LSM). The benefit of this developed LSM approach is in her non-iterative process. Then, the obtained initial values will be optimized through our developed hybrid approach (Levenberg-Marquardt with PSO). The curve characteristic of the PV generator has two distinct regions as shown in Figure 9, Linear and Non-linear parts. For the linear part, the LSM method is applied merely, while in the non-linear part, it is done through a suitable approximation by a linearization in a logarithmic way [26].

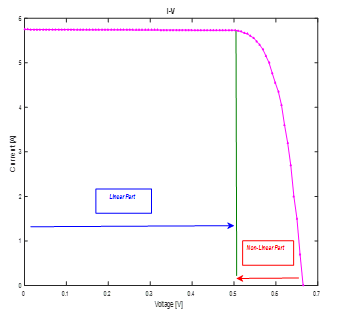Figure 9. Linear and Non-Linear parts of the I-V characteristic.

The Least Squares Mean approach is based on the minimization of a quadratic function defined as below [14].

Where  is defined as the prediction error between the PV model and the real PV system [14].

In order to identify the PV parameters from the real I-V characteristics, we fitted to the best the model to the real (I-V) data, through the minimization of squared errors between the theoretical and experimental curves [27]. In this regard, the cost function used in the optimization process is the Sum of Squared Error (SSE) [28]. Where I_Model is the output vector of the PV model, I_Real is the PV measured process output and N is the total number of the measured points.

Where: X is a vector that contains the PV parameters, for example, {I_L, I_ds1, I_ds2, n_1, n₂, R_s, R_sh}, in the two-diode model. The minimum of Sum Squared Errors “SSE” leads to optimal values of the PV parameters [28]. The minimization of the objective function cannot be done in analytically way due to the strong nonlinearity of the I-V curve characteristics. Therefore, the numerical methods for the nonlinear regression based on the least squares principle are more appropriate to minimize such function.

• The Levenberg-Marquardt (LM)

The traditional technic of Levenberg-Marquardt contains inside its process two technics declined from Gradient orders such as the steepest descent and the Gauss-Newton with their complementary features [29]. Generally, the LM approach starts through the steepest descent technic because of her low sensitivity for initial parameters values. Then, after calculating the parameters values and near approaching to the final solution, the Gauss-Newton technic take over and lead to end of the LM process, with a fast convergence. The control parameter  called damping factor is the responsible parameter in the LM approach that allows switching from steepest descent to Gauss-Newton. The PV parameters to be determined as in [30], are updated at each iteration using the following expression [29].

Where

• J: Jacobian matrix [  which contains a derivative for the function f(I,V,X) regarding each parameter.
• I: Identity matrix.

The damping factor, which his value must be found at each iteration of Levenberg-Marquardt approach, is considered as a crucial factor in the convergence process of the algorithm, for this reason we optimize their value by using PSO approach.

• The Particle Swarm Optimization approach (PSO)

This subsection focuses on the evolution study of the function , indicated by  for  fixed at X_k, regarding many diverse values of the damping factor, at each iteration of the Levenberg-Marquardt algorithm. Herein, it is observed that at each iteration, a presence of various local minimums of . For this reason, and in order to achieve the global minimum of  corresponding to the best minimizing of the objective function , we suggest using the PSO approach.  The basic idea of this latter approach was inspired from social behaviour of certain animals such as birds, fishes, and ants and so on. The PSO process is like the natural process existing in groups when they are communicating together, such as a group of birds when they search for migration way or such as ants when they search for food. Herein, it is observed that those animals or insects do not know their best position. Consequently, if a certain member can find the best way to go and achieve the objective, the rest of members, will follow [31]. For mathematical modelling of PSO approach, the population is called a swarm, the individuals are termed as particles and the objective function to be optimized is called fitness. Each particle possesses:

• 

The following Flowchart, Figure 10, shows the major steps of the PSO’s algorithm.

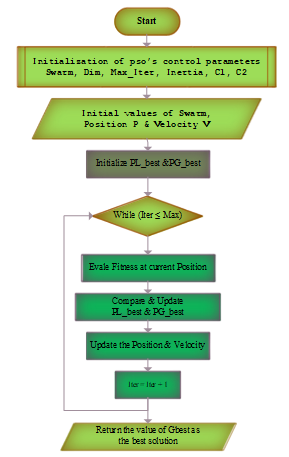Figure 10. Flowchart of the general steps of PSO algorithm.

This algorithm requires a number of parameters to be set, namely, Inertia W, velocity V, position P, local and global components C₁ & C₂, Number of search agents (the swarm of N visited sites), Maximum number of iteration and the stopping criterion.

• The hybridization of LM with PSO

The PV identification process, including initialization of PV parameters values through LSM and then optimize their values through the combined Levenberg-Marquardt with Particle-Swarm-Optimization (LM-PSO) developed approach is presented step by step, in what follows Figure 11.

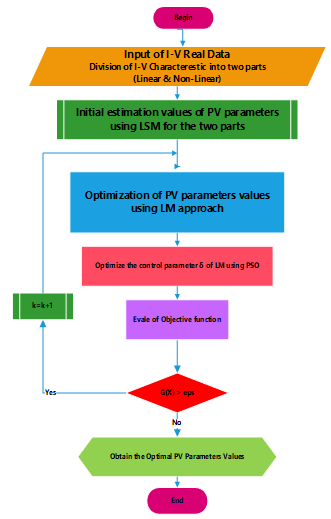Figure 11. PV parameters identification steps using the hybrid LM approach with PSO approach.

The organigramme of Figure 11 resume the PV parameters identification steps done in this work. After obtaining real data through the acquisition work we used them in a process of algorithms, such as the LSM and the hybrid optimization approach. The advantage of hybridization of two optimization technics is observed in the optimization process of the damping factor of the LM technic, at each iteration, using the PSO technic.

2.4.  Fourth Step “Validation of the model”

      After the estimation process, the obvious query is whether the derived model is adequate for its intended use or not. This is the subjective and overall hard problem of model validation [32]. The sound way to attack the matter is to confront the model with all available type of information, including a priori knowledge, experimental data, and experience of the used model. The selected PV model from the steps before will be validated in this final identification step, after attaining the final obtained results and once fitting all of the entire curve characteristics. The developed approach was tested for other real data of PV cells such as (A-300 of SunPower) as shown in the Figure 12 below, for the one diode model, at STC: Standard-Test-Conditions (T=25°c & G=1000W/m²).

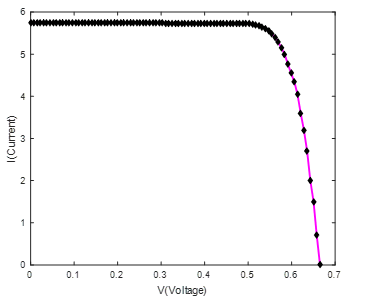Figure 12. The fitted I-V curve characteristic for the (A-300 SunPower) solar PV cell at STC.

From the above Figure 12, it is clear that once obtaining a good confrontation between the two curves, the model is well chosen to represent the real system.

4. Results & Discussions

This section presents the results obtained for identifying PV parameters values, using the developed combined approach. The following Table II illustrates the results obtained for the electrical PV parameters values of the generator installed in our Laboratory (LDCCP).

Table 2. The obtained parameters values from our developed approach for PV generator.

(a) The one diode model

Parameters	Obtained values
IL Ids n Rs Rsh	2.45 3.166611e-07 1.279182 0.036461 53.271523

 (b) The double diode model

Parameters	Obtained values
IL Ids1 Ids2 n1 n2 Rs Rsh	2.45 3.166611e-07 3.266611e-07 1.279182 1.379182 0.036461 53.271523

The two above tables show that the obtained values for PV parameters models have good values as compared to the values mentioned in literature [33]. The final curves results that validate the model selected for representing our PV generator’s behavior, are shown in the fitting I-V curves below, Figure 13.

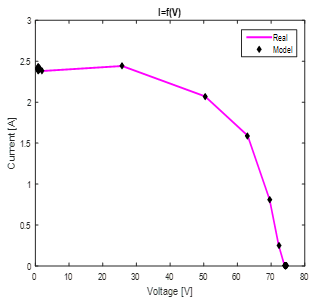Figure 13. The fitted final I-V curve characteristic for our PV generator (4 associated modules in series of SM55).

It is clear from Figure 13 that the two curves (from the model and the real systems) are well fitted and adjusted. Therefore, the selected model is approximately near of the real behavior of PV generator.

5. Conclusion

In this paper, a detailed study is provided for determining, estimating, identifying and obtaining of the electrical PV parameters values in real time, through combining two algorithms (Levenberg-Marquardt with Particle-Swarm-Optimization). The novelty of this method is that it uses least-squares regressions to initialize the PV parameters values before optimizing their values. The process of identification was elaborated with details, containing all of the four basic steps of identification, as data acquisition, selection of model, PV parameters estimation values and model validation. The obtained results show that the developed approach has the capability to achieve higher PV parameters values with a best precision. The effectiveness is proved by the best approximation obtained between the real data and the data predicted from the curve fitted. This work allows as studying the PV generator’s behavior under real conditions, through the detailed steps of the identification process.

Conflict of Interest

The authors declare no conflict of interest.

Acknowledgment

The experimental part presented by this paper was done at the LDCCP Laboratory of the Electronic Departement at Ecole Nationale Polytechnique, Algiers, Algeria.

1.  S. Tchoketch Kebir, M. S. AIT CHEIKH, M. Haddadi, B. Boumaaraf, “Step by step Parameters Identification for Photovoltaic Generator” in the 5th International Conference on Electrical Engineering – Boumerdes (ICEE-B), Boumerdes, Algeria, 2017.
2.  Karel J. Keesman, System Identification: an introduction, Springer-Verlag London, 2011.
3.  I.D. Landau. System identification in closed loop. Marie Curie Action TOK 3092, 2004.
4.  Gonzalo Cabodevila, Identification des systèmes, École Nationale Supérieure de Mécanique et des Microtechniques, France, 2010.
5. Ali M. Humada, Mojgan Hojabri, Saad Mekhilef, Hussein M. Hamada, “Solar cell parameters extraction based on single and double-diode models: A review”. Renewable and Sustainable Energy Reviews, Volume 56, April 2016, Pages 494-509.
6.  M.A. Hasan S.K. Parida, “An overview of solar photovoltaic panel modeling based on analytical and experimental viewpoint”. Renewable and Sustainable Energy Reviews Volume 60, July 2016, Pages 75-83.
7.  J. Thongpron, K. Kirtikara, C. Jivacate. “A method for the determination of dynamic resistance of photovoltaic modules under illumination”. Solar Energy Materials & Solar Cells 90 (2006).
8.  Vincenzo d’Alessandro, Pierluigi Guerriero, Santolo Daliento, Matteo Gargiulo. “A straightforward method to extract the shunt resistance of photovoltaic cells from current–voltage characteristics of mounted arrays“. Solid-State Electronics 63 (2011) 130–136.
9.  Kenneth, L. Kennerud. “Analysis of Performance Degradation in CdS Solar Cells“. IEEE Transactions on aerospace and electronic systems. NOVEMBER 1969.
10.  Valerio Lo Brano, Giuseppina Ciulla, “An efficient analytical approach for obtaining a five parameters model of photovoltaic modules using only reference data”. Applied Energy Volume 111, November 2013, Pages 894-903
11.  T.R. Ayodele, A.S.O. Ogunjuyigbe, E.E. Ekoh, “Evaluation of numerical algorithms used in extracting the parameters of a single-diode photovoltaic model”. Sustainable Energy Technologies and Assessments Volume 13, February 2016, Pages 51-59.
12.  F.Ghani G.Rosengarten M.Duke J.K.Carson, “The numerical calculation of single-diode solar-cell modelling parameters”. Renewable Energy Volume 72, December 2014, Pages 105-112.
13.  Alireza Askarzadeh, Alireza Rezazadeh, “Parameter identification for solar cell models using harmony search-based algorithms”. Solar Energy Volume 86, Issue 11, November 2012, Pages 3241-3249.
14.  M.F. AlHajri, K.M. El-Naggar, M.R. AlRashidi, A.K. Al-Othman, “Optimal extraction of solar cell parameters using pattern search”. Renewable Energy Volume 44, August 2012, Pages 238-245.
15.  M.Zagrouba, A.Sellami, M.Bouaïcha, M.Ksouri, “Identification of PV solar cells and modules parameters using the genetic algorithms: Application to maximum power extraction”. Solar Energy, Volume 84, Issue 5, May 2010, Pages 860-866.
16.  D. Ucinski, Optimal Measurement Methods for Distributed Parameter System Identification: CRC Press; 1 edition (August 27, 2004), 2004.
17.  O. Nelles, Nonlinear System Identification: from classical approaches to neural networks and fuzzy models, 1 ed.: Springer-Verlag Berlin Heidelberg, 2001.
18.  M. Benghanem, “Low cost management for photovoltaic systems in isolated site with new IV characterization model proposed,” Energy Conversion and Management, vol. 50, pp. 748-755, 2009.
19.  https://store.arduino.cc/arduino-uno-rev3
20.  H. Belmili, M. S. Ait Cheikh, M. Haddadi, and C. Larbes, “Design and development of a data acquisition system for photovoltaic modules characterization,” Renewable Energy, vol. 35, pp. 1484-1492, 2010.
21.  http://www.siemen.co.uk/sm55_sm50.html
22.  Hongmei Tian, Fernando Mancilla-David, Kevin Ellis, Eduard Muljadi, Peter Jenkins, “A cell-to-module-to-array detailed model for photovoltaic panels”. Solar Energy, Volume 86, Issue 9, September 2012, Pages 2695-2706.
23.  K. Ishaque, Z. Salam, and H. Taheri, “Simple, fast and accurate two-diode model for photovoltaic modules,” Solar Energy Materials and Solar Cells, vol. 95, pp. 586-594, 2011.
24.  Mohsen Taherbaneh ,A. H. Rezaie,H. Ghafoorifard,K. Rahimi Iranian, Iran,M. B. Menhaj &J. M. Milimonfared, “Evaluation of two-diode-model of a solar panel in a wide range of environmental conditions”. International Journal of Electronics, Volume 98, Issue 3, 2011.
25.  K. Madsen, H.B. Nielsen, O. Tingleff, Methods for Non-Linear Least Squares Problems, 2nd Edition, April 2004.
26.  K. Bouzidi, M. Chegaar, A. Bouhemadou. “Solar cells parameters evaluation considering the series and shunt resistance”. Solar Energy Materials & Solar Cells 91 (2007) 1647–1651.
27.  K.F. Alvina, A.N. Robertson, G.W. Reichc, K.C. Parkd, “Structural system identification: from reality to models”. Computers & Structures Volume 81, Issue 12, May 2003, Pages 1149-1176.
28.  Valerio Lo Brano, Giuseppina Ciulla, and Mariavittoria Di Falco. “Artificial Neural Networks to Predict the Power Output of a PV Panel”. Volume 2014.
29.  Henri P. Gavin. “The Levenberg-Marquardt method for nonlinear least squares curve-fitting problems”. Department of Civil and Environmental Engineering. May 4, 2016.
30.  A. Malaoui, A. Elmansouri, “Deux nouvelles methodes complementaire pour l’extraction optimale des parametres electriques des jonctions”. Revue des Energies Renouvelables Vol. 13 N°2 (2010) 199-212.
31.  Satyobroto Talukder. “Mathematical Modelling and Application of Particle Swarm Optimization”. Blekinge Institute of Technology, Master of Science, February 2011.
32.  Peter Lindskog. “Algorithms and Tools for System Identification Using Prior Knowledge”. Linköping University, September 1994.
33.  Kashif Ishaque, Zainal Salam, Hamed Taheri, Amir Shamsudin. “A critical evaluation of EA computational methods for Photovoltaic cell parameter extraction based on two diode model”. Solar Energy 85(9):1768-1779 · April 2011.

(Click Here)

(Click Here)