1. Introduction

Stream cipher by Reed-Solomon (RS) code this work intends to implement encryption by encoding if necessary [1]. As the encoding-encryption paradigm has been used in the standard for mobile telephony GSM [2, 3], it has received much attention so far. RS code has been widely used in communications and storage systems to correct errors, which can also be used together with BCH code to ensure data integrity [4]. The idea of using RS code as a carriage for stream cipher comes from the observation of RS code for code-based cryptography, where it is found that the errors are intentionally inserted and recovered with much computation and energy [5, 6]. In fact, the code-based peudo RS code is used to reduces the density of a transform matrix and improves weakly secure data exchange.

Stream cipher belongs to symmetric cryptography and can be built by many devices, such as linear and nonlinear feedback shift registers. For example, the Rakaposhi stream cipher consists of a 128-bit nonlinear feedback shift register, a 192-bit dynamic linear feedback shift register, and a nonlinear filter function [9]. Ubiquitous environments demands security, speed and power consciousness in processing huge amount of multimedia data [10], in which stream cipher can be used. Stream cipher is an engine that generates bit streams to mix the message. At the sending part, the plain text is confused with one bit stream, while at the receiving part, the cipher text is processed with the same bit stream again to recover the message. The stream cipher is like a determined peudo-random discrete function, of which the security can be analyzed by the generating mechanism of the cipher. A stream cipher can be marked by a key stream (K) and the initialization vector (IV ), while the adversary may recover all the secret bits of K after observing many related (K,IV ) pairs [9].

Usually, an one-way function and multiple steps are devised to safeguard the key generations or initialization processes, let bit XOR as the only operation to encrypt the message. By contrast, people also seek approaches to implement more secure code by public key cryptography. Code based cryptography [11] with Goppa codes [12] or MDPC codes [13], for example, can be applied to realize McEliece system . Meanwhile, generalized RS code can also be used to implement asymmetric cryptography [6], which brings out short keys compared with that obtained by Goppa code.

In this work, a stream cipher with RS code is proposed, in which the messages are encoded as RS codewords. This idea comes from its similarity to the configured logic with a DSP unit in FPGA. At the receiving part, the plaintexts and cipher are recovered from RS codes. The contributions of this paper include:

• a mechanism to include stream cipher in RS encoding and decoding, which is able to cover the message in a simple way.
• a review of related work about stream cipher of different schemes.
• a hardware implementation of stream cipher along by RS code.

The remaining parts of this paper is organized as follows: Sect. 2 is a review of RS encoding and decoding; Sect. 3 briefly introduces the related work with stream cipher and code-based cryptography; Sect. 4 discusses the stream cipher along with RS code; then the hardware implementation and comparison of the stream cipher are given in Sect. 5; the last section concludes this paper.

2. RS Code

RS code is widely used for error corrections. The encoding can be either implemented by polynomial division with shift registers, or it can be performed by multiplying the generating matrix [14]. Suppose the RS code is defined over GF(2^m) with n code bits and k information bits. Message sequence (u_k−₁,…,u₁,u₀) is equivalent to

 Let the parity check code be (v₀,v₁,…,v_n−_k−₁), with v(X) = X^n−ku(X) mod g(X), then the code polynomial yields c(X) = Xn−ku(X)+v0 ·Xn−k−1 +v1 ·Xn−k−2 +···+vn−k−1,

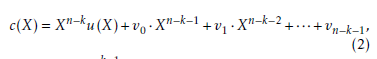imum number of error corrections. Then the encoded symbols will read (v_n−k−₁,…,v₀,u_k−₁,…,u₀), with v_i and u_i being symbols in GF(2^m).

Suppose the code generator is expressed as g(X) =

2t

Q (X −αi) = g0 + g1X + ··· + g2t−1X2t−1 + X2t. Then i=1

           2t                                     2t 16j62t

g₀ = ^Q αⁱ, g₁ = ^{− P Q} α^j. For 2 6 i 6 2t ⁻ 1, the i=1                     i=1 j,i

generator polynomial can be computed in Galois field recursively. In Matlab, the generator polynomial can be computed directly by function rsgenpoly.

Once the generator is calculated, the generator matrix can be obtained. Take n = 255, k = 223, t = 16, and m = 8, then the generating matrix can be computed in Matlab as follows:

n= 255; k= 223; t= 16; m= 8; tvc= zeros(1, 33); tvc= [ 45 216 239 24 253 104 27 … 40 107 50 163 210 227 134 …

224 158 119 13 158 1 238 …

164 82 43 15 232 246 142 …

50 189 29 232 1];

gvc= gf(tvc, m); dv= gf(zeros(k, n- k)); qv= gf(0, m); gpc= fliplr(gvc); for i= 0: 1: k-1

tmpv= gf([1, zeros(1, n- k+ i)], m); [Q, R]= deconv(tmpv, gpc); length1= length(R ); indx= find(R˜=gf(0, m), 1, ’first’); dv(i+1, n- k- length1+ indx: n- k)

= R(indx: length1); end

gtx= gf(zeros(k, n), m); % gtx is the generating matrix gtx(:, 1: n-k)= fliplr(dv); gtx(:, n- k+ 1: n)= gf(eye(k, k), m);

The encoding of RS code can be computed as modular division in the polynomial field [14]. Let b(X) = X^n−ku(X) mod g(X), then b(X)+X^n−ku(X) can be divided by g(X) and become a RS code polynomial. The symbol u₀ with the lowest index is usually processed as the symbol with the highest weight for convenience.

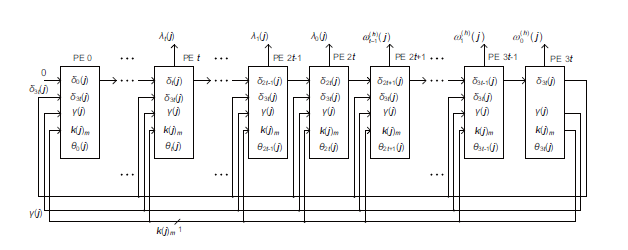Figure 1: System architecture to solve error location polynomial [16, 1].

The RS decoding is divided into four steps, i.e., syndrome computation, solution of error location polynomial, Chien search, and determination of the error values by Forney’s algorithm. RS code is defined in the extension field GF(2^m·s), and syndromes can be computed according to [15]:

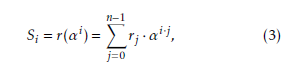The error polynomial can be obtained by the improved inversion-less Berlekamp-Massey algorithm [16]. The resulting error polynomial reads

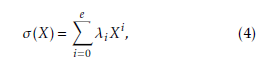where ν 6 t. λ_i is used to calculate the error locations. The error values are

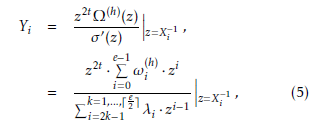where Ω^(h)(z) = e^P−1ω_i^(h)(z)·zⁱ, the symbol h denotes the

i=0

higher partial products from z^2t to z^2t+e−1, and e is the number of error locations.

The system architecture of RS decoding [16, 1] is shown in Fig. 2. First, the original passages through processing elements are replaced by direct connections of signals. Second, the control logics are totaly integrated into the last processing element for simplicity. The signal k(j)_m is the sign bit of the integer k(j), where m denotes the m-th bit. The coefficients from λ_t to λ₀ come out of from PE t to PE 2t, while the coefficients

from ω_t−₁ to ω₀                    are produced from PE 2t +1 to PE 3t.

Among the processing elements, there exists matrix products. Typically, the matrix multiplication [α^m,α^m+1,…,α^2m−2]^T = Q ^· [1,α,…,α^m−1]^T , the GF(2^m) can be computed according to C = A · B = (L + Q^T · U) · B proposed in [17]. In Matlab, the matrix Q in GF(2⁸) can be obtained in the following:

Tx= zeros(m-1, m);

Ty1= zeros(m, m); vf0= [1, 0, 1, 1, 1, 0, 0, 0];

Ty(:, 1: m-1)= [zeros(1, m-1); eye(m-1)];

Ty(:, m)= vf0.’;

Ty1= Tyˆm;

Ty1= mod(Ty1, 2);

Tx= Ty1(:, 1: m-1).’; Q= Tx;

The Chien search circuit is composed of t multipliers in GF(2^m) and a few adders. It is used to find out the error locations by a full search if λ_i , 0.

3. Related Work

The popular stream cipher consists of two key stream generators, as is shown in Fig. 2 [18, 19]. The plaintexts are masked by the keys on the left, and then decrypted by the same stream on the right. The symbol ‘IV’ denotes initialization vector.

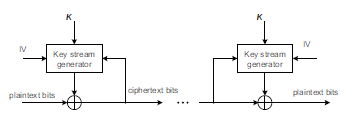Figure 2: Traditional stream cipher by two key generators.

A random number generator (RNG) can be implemented by the linear feedback shift register (LFSR)[20] that generates peudo-random numbers for stream cipher, as is shown in Fig. 3. In practise the RNG can also be constructed by other digital or analog circuits.

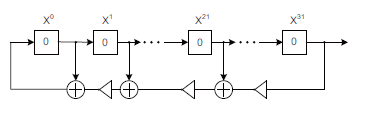Figure 3: Linear feedback shift registers by XNOR gates[21].

A light-weight and energy-friendly stream cipher is proposed for wireless sensor network (WSN) in [18]. The paper suggests use the linear combination of pervious packets to generate the peudo-random key bits in a stream cipher, where a mixed protocol is advanced and public key is used to achieve data privacy [18].

Joint encoding and encryption by LDPC codes and RS codes for public key cryptography is a tradeoff between security and reliable communication [5, 22, 6]. New scrambling and permutating matrices for McEliece system with RS codes are proposed in [6] to enhance security. In [2] the wire-tap encoding and the error correction encoding are concatenated to enhance security. And in [3], a generator matrix, an invertible matrix, and gamma generator are used to produce the ciphertexts.

A provable secure stream cipher based syndrome decoding problem is presented in [7], which uses regular words to speed the system up and quasi-cyclic codes to reduce memory requirements. The results seem to be based on quasi-cyclic BCH codes.

4. Proposed Approach

Now suppose the message piece is r and the random numbers s are combined or XORed, then one can encode (r⊕α·s), where α is the multiple of s or a u×v matrix with u = s/w, v = r/w and w is the width of a symbol. Next, one piece of the symbols s is inserted by addition modulo 2^m, and the new message reads r⁰ = M +s. At the other terminal, by RS decoding one can recover s as well as (r + αs). Finally, the r = (r + αs) − αs can be restored. The whole process is shown in Fig. 4. Especially, the insertion of errors avoids zero bytes by changing them as nonzero bytes within random numbers.

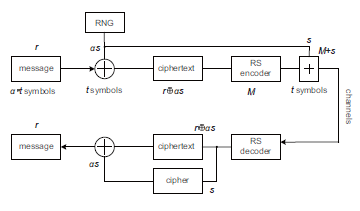Figure 4: Stream cipher by RS code.

First, the security of a code-based system can be seemed as a public-key security problem, while the usual stream cipher is a symmetric cryptosystem. The proposed mechanism embeds the stream cipher along Reed-Solomon codes looking like a public-key cryptography: considering the key streams as private keys for encoding, and looking at the RS code parameters as the public key to decrypt the ciphertexts.

The security of the proposed scheme may also be improved by the application of shortened codes. In this way, the n-symbol codewords are replaced by a (n−δ)-symbol codewords. Take the wireless communication for example, the sender and receiver share the same hardware units, i.e., stream engines, encoders and decoders. Then, the stream cipher with the sender can be seen as private keys to encrypt the messages. The choices of (1) whether a subfield subcode is chosen

(2) whether a shortened code is chosen (3) whether the same decoder exists can be used as the public keys. If the decoder exists and the other two parameters are rightly chosen, then the stream cipher can be separated from the message bits by RS decoding.

In detail, one can use subcode or shortened code to decrease the error rate or improve the security of the system, as is shown in Fig. 5. The subfield subcode over GF(p^s) have the same length n but is smaller than its parent code [23] with the word width, which is compressed from dsmlog₂pe to dslog₂pe. In fact, the length n of a subfield subcode may be larger than the size of a subfield, but is constrained its parent field size. Notice that the parity check symbols keep about double word size of other code symbols in Fig. 5.

6XEFRGH

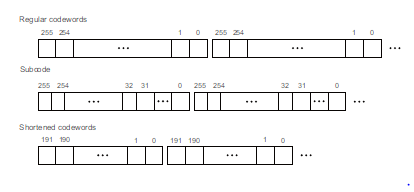Figure 5: Stream cipher by subcode or shortened RS codes.

Secondly, the proposed scheme reduce the hardware cost and complexity by reusing the encoder for encryption and recovering the key streams by the decoder. Therefore, the task of aligning the stream engines to time sequence becomes unnecessary. As the number of stream cipher engines decreases from 2 to 1, it reduces the continuous power consumption much. On the one hand, it reduces the hardware units by a half; on the other hand, the renewal frequency of the stream cipher engine can be lowered down. Also, it is not easy to align the messages to real time, but it is feasible to align the messages at code sequence. The oscillator frequency may vary from time to time, while the stream cipher engines requires accurate alignments. The existence of time delay in mobile phones proves the validity of code alignment.

Furthermore, if the function of RS decoding and encoding is occasionally used, then the encryption can be used as an auxiliary function. Otherwise, if the error correction through the transmission path is requirable, then the first few code symbols can be designated as masks of key streams while the next words can be corrected by the remained error correction capability. Since error correction logic and stream cipher are basic units in wireless communications, this scheme

VHFUHWGDWDDVVWUHDPFLSKHU 00000000h: 31 30 38 3D 33 5E 33 2A 32 5E 32 0D 0A 0D 0A ; 108=3^3*2^2… PHVVDJH 00000000h: 54 48 65 20 57 61 74 65 72 20 4D 61 72 67 69 6E ; THe Water Margin 00000010h: 20 74 65 6C 6C 73 20 74 68 65 20 73 74 6F 72 79 ;  tells the story 00000020h: 20 6F 66 20 72 65 62 65 6C 6C 69 6F 6E 20 61 6E ;  of rebellion an 00000030h: 64 20 73 74 72 75 67 67 6C 65 20 6F 66 20 73 6B ; d struggle of sk 00000040h: 69 6C 6C 65 64 2C 20 62 72 75 74 65 2C 20 6F 72 ; illed, brute, or 00000050h: 20 62 72 61 76 65 20 6D 65 6E 20 69 6E 20 61 63 ;  brave men in ac 00000060h: 69 65 6E 74 20 43 68 69 6E 61 2E 20 54 68 65 79 ; ient China. They 00000070h: 20 61 72 65 20 6E 61 6D 65 64 20 4A 69 61 6E 67 ;  are named Jiang 00000080h: 20 53 6F 6E 67 2C 20 4A 75 6E 79 69 20 4C 75 2C ;  Song, Junyi Lu, 00000090h: 20 53 68 65 6E 67 20 47 6F 6E 67 73 75 6E 2E 2E ;  Sheng Gongsun.. 000000a0h: 2E 0D 0A 0D 0A 0D 0A                            ; ……. PHVVDJHHQFU\SWHGE\VWUHDPFLSKHU 00000000h: 65 78 5d 1d 64 3f 47 4f 40 7e 7f 6c 78 6a 63 6e ; ex]d?GO@~lxjcn 00000010h: 11 44 5d 51 5f 2d 13 5e 5a 3b 12 7e 7e 62 78 79 ; !D]Q_-!^Z;!~~bxy ĂĂ Figure 6: Hiding information as stream cipher in RS codes. Table 1: Advantages of Proposed Stream Cipher Compared to Other Schemes Reference Function Implement Topology ENC/DEC Symmetry Reuse ECC for No. of RNG Randomness Code This work Stream data Hardware 1-to-N Not full Yes 1 Not strictly RS [10] Stream data Hardware 1-to-1 Symmetric No 2 Required No [7] Stream data Software 1-to-1 Symmetric No 2 Required Quasicyclic [8] Exchange data Software N-to-N Not No 0 – GRS

combines their functions.

Thirdly, it may be applicable to transmit extra data through the key streams and therefore increase the throughput of inserted codewords. For example, the (255,223,16) RS code has 223 information symbols. If the encoder are used for stream cipher, then 16 symbols of information can be added to the codeword secretly. The information rate is increased from 223/255 = 0.87 to 239/255 = 0.94. As is shown in Fig. 6, it is able to mix information with secret data in the proposed codes.

5. Comparison

The comparisons of this work compared with peer works are shown in Tab. 1. It should be noticed that the proposed scheme is not full symmetric, for which the cipher is decoded through the public-key. The architecture is implemented in a topology of 1-to-N, with N being any natural numbers including 1. If N = 1, then there are two parties to communicate with each other; or else it can be used in a network. By contrast, the stream cipher is usually supposed to follow 1-to-1 topology. While the encoding and decoding architectures in our work are non-symmetric, the whole stream cipher engine can be made nearly symmetric by integrating an encoder and decoder together. Moreover, this work needs only 1 random number generator while other stream ciphers requires 2 to N random number generators, since the key stream is embedded in the data stream in this work.

The weakly secure data exchange problem with generalized Reed-Solomon code is discussed in [8], in which data exchange between multiple parts rather than two parts are considered.

Also, in the proposal the random number generator is not that strictly required and pseudo random numbers can be used, while other works pay much attention to the random number generator itself, owing to different mechanism for stream ciphers. While traditional stream cipher uses continuous random bits, this work applies data structures of codewords to separate data. The references [8, 7] also uses GRS codes and quasi-cyclic codes to encode data and bring out randomness.

The architecture and hardware implementation results with [10] is demonstrated in Tab. 1 and Tab. 2. It uses a hardware common key cryptography named RAC for stream cipher, where the random numbers are used as addresses to relocate the data bits. The random numbers are generated by the recipient as addresses to resort the received ciphertext. Assuming the stream cipher engine in [10] works in a pipeline, then it is able to encrypt and decrypt 1 byte every clock cycle with throughput up to 3.2 Gps. Nevertheless, considering that the data from the sender or to the recipient should be stored in a RAM for reorganization, so the real decryption throughput may be only a half, let alone the time for fetching instructions.

Finally, the power consciousness of this design is demonstrated by the application of RS code, whereas McEliece systems usually use nonsystematic encoding with an increase of computational efforts by n/(n−k) times. In addition, if there are demands of error corrections for channels, the hardware units may be reconfigured and reused at different times.

Table 2: Hardware Implementation of Stream Cipher Engine by Reed-Solomon Code.

Design            Platform                  LUTs               fmax          Throughput

Dec                 XC5VLX85-2            5253               270      0.289

Enc/Dec           XC5VLX85-2            5905               270         1.82/0.289

[10]                 0.18 µm CMOS         1.38 mm²            400      1.6∼ 3.2

The stream cipher with encoding and decoding by RS codes is described by Matlab for test at first, then it is described by Verilog HDL for hardware implementation. As is shown in Tab. 2, the stream cipher engine is simulated by Modelsim 6.2, synthesized by Synopsys Synplify Pro 2014, and placed and rooted in Xilinx ISE 14.7. The code parameters are chosen as usual in [24],

i.e.,

m = 8: number of bits per symbol, n = 255: number of symbols per codeword, k = 223: number of message symbols in a codeword, t = 16: number of corrected errors by symbols.

According to the theory and results in [7], the security level of the cipher in the above table is about 80 bits of keys with symmetric cryptography.

In Tab. 2, the RS code supports correcting 16 symbols of errors along with 223 symbols of messages. It takes about 3.78 µs to correct 2 errors of symbols, and 7.06 µs to correct 16 errors of symbols. Its information throughput without parity check bits are 1.59/0.253 Gbit/s respectively for encoding and decoding.

6. Conclusion

Stream cipher is often used for mobile communications between two parties. In general, this paper proposes an easy scheme to implement stream cipher along with the popular RS code, which relies on RS encoding and decoding to cover and uncover the key streams. It is beneficial to easily evaluate the complexity and enhance the security of communication systems. The proposed cipher is based on the NP-complete problem of decoding a random linear code, which simply conforms to many solved code-based security issues. The cipher also decreases one key generator and reduces unnecessary power consumption for the synchronization between parties.

Acknowledgment

The author would like to appreciate the editor and reviewers for their kind help. This work is supported by Shenzhen postdoctoral base for innovation and practice and partly by Shenzhen basic research program

1.  T. Wu and R. Wang, “Stream cipher by Reed-Solomon code,” in International Conference on Information and Communication Technology Convergence (ICTC), 2017, pp. 422–427.
2.  F. E. Oggier and M. J. Mihaljevic, “An information-theoretic analysis of the security of communication systems employing the encoding-encryption paradigm,” arXiv, 2018. [Online]. Available: http://arxiv.org/abs/1008.0968
3.  A. N. Alekseychuk and S. V. Gryshakov, “Secure and practical randomized stream ciphers based on ReedSolomon codes,” Cybernetics and Systems Analysis, vol. 53, no. 2, pp. 262–268, 2017.
4.  S. Lin and J. Daniel J. Costello, Error Control Coding. Upper Saddle River, New Jersey: Pearson Education, Inc., 2004.
5. M. Baldi, QC-LDPC Code-Based Cryptography, ser. Briefs in Electrical and Computer Engineering. Springer, 2014.
6.  M. Baldi, F. Chiaraluce, M. Bianchi, and J. R. D. Schipani, “Enhanced public key security for the McEliece cryptosystem,” Journal of Cryptology, vol. 29, no. 1, p. 127, January 2016.
7.  P. Gaborit, C. Lauradoux, and N. Sendrier, “SYND: a fast codebased stream cipher with a security reduction,” in IEEE International Symposium on Information Theory, 2007, pp. 186–190.
8.  M. Yan, A. Sprintson, and I. Zelenkoy, “Weakly secure data exchange with generalized reed solomon codes,” in IEEE International Symposium on Information Theory, 2014, pp. 1366–1370.
9.  M. Orumiehchiha, J. Pieprzyk, E. Shakour, and R. Steinfeld, “Security evaluation of Rakaposhi stream cipher,” in International Conference on Information Security Practice and Experience (ISPEC 2013), ser. Lecture Notes in Computer Science, R. Deng and T. Feng, Eds., vol. 7863. Berlin, Heidelberg: Springer, 2013, pp. 361–371.
10.  M. Fukase, H. Takeda, R. Tenma, K. Noda, Y. Sato, R. Sato, and T. Satot, “Development of a multimedia stream cipher engine,” in International Symposium on Intelligent Signal Processing and Communication Systems (ISPACS2006), Tottori, Japan, 2006, pp. 562–565.
11.  H. C. van Tilborg, Fundamentals of cryptology: A Professional Reference and Interactive Tutorial. Boston/Dordrecht/London: Kluwer Academic Publishers, 1999.
12.  T. Eisenbarth, T. Guneysu, S. Heyse, and C. Paar, “Microeliece: Mceliece for embedded devices,” in CHES, ser. LNCS, vol. 5747, 2009, p. 4964.
13.  S. Heyse, I. von Maurich, and T. G¨uneysu, “Smaller keys for code-based cryptography: QC-MDPC McEliece implementations on embedded devices,” in CHES, ser. LNCS, vol. 8086, 2013, pp. 273–292.
14.  S. Lin and J. Daniel J. Costello, Error Control Coding- Fundamentals and Applications. New Jersey: Prentice Hall, 1983.
15.  B. Sklar, “Reed-solomon codes,” 2001. [Online]. Available: http://ptgmedia.pearsoncmg.com/images/art sklar7 reed-solomon/elementLinks/art sklar7 reed-solomon.pdf
16.  D. V. Sarwate and N. R. Shanbhag, “High-speed architectures for reedsolomon decoders,” IEEE Transactions on VLSI Systems, vol. 9, no. 5, pp. 641–655, October 2001.
17.  A. Reyhani-Masoleh and M. A. Hasan, “Low complexity bit parallel architectures for polynomial basis multiplication over GF(2m),” IEEE Transactions on Computers, pp. 945–959, 2004.
18.  H. Lin, A. J. A., D. Bai, and Y. Liu, “A light-weight stream cipher for wireless sensor networks,” in Future Wireless Networks and Information Systems, ser. Lecture Notes in Electrical Engineering, Y. Zhang, Ed., vol. 143. Berlin, Heidelberg: Springer, 2012, pp. 627–638.
19.  B. Sklar, Digital Communications Fundamentals and Applications. Beijing: Publishing House of Electronics Industry, 2015, in Chinese.
20.  A. Canteaut, “Linear feedback shift register,” pp. 726–729, 2011, reference Work Entry.
21.  “Linear feedback shift registers in virtex devices,” 1996. [Online]. Available: http://www.xilinx.com/support/ documentation/application notes/xapp052.pdf
22.  M. Esmaeili and T. A. Gulliver, “Joint channel codingcryptography based on random insertions and deletions in quasi-cyclic-low-density parity check codes,” IET Communications, vol. 9, no. 12, pp. 1555–1560, 2015.
23.  J. I. Hall, http://users.math.msu.edu/users/jhall/classes/ codenotes/Subfields.pdf, Michigan State University, pp. 89– 99, 2012, codes over Subfields.
24.  Z. Liang andW. Zhang, “Efficient Berlekamp-Massey algorithm and architecture for Reed-Solomon decoder,” Journal of Signal Processing Systems, vol. 86, p. 5165, 2017.

(Click Here)

(Click Here)