1. Introduction

Space exploration and aging induce physical deconditioning. Space exploration has been limited so far to a low Earth orbit and short visits to the Moon, but deconditioning will become more serious after lengthy exposure to microgravity and hypogravity in manned spaceflights to Mars and bases there and on the Moon. Effective and efficient countermeasures within limited spaces such as those in spaceships are indispensable for maintaining human health. This report extends the work that was originally presented at IEEE EMBC 2017 [1].

A method of creating countermeasures against microgravity and hypogravity must be established to safely generate effective outcomes. Ergometer exercise reduces the load imposed by gravitational force on leg joints and the metabolic cost is comparable to that of walking on a level surface [2]. This type of exercise is beneficial for persons with knee osteoarthritis and elderly individuals seeking to engage in cardiovascular training. However, such exercise is ineffective for maintaining musculoskeletal function during spaceflight because the mechanical load provided by aerobic exercise is too low to prevent muscle atrophy at 0 g [3]. Preventing bone loss requires a compressive load along the bone axis similar to the repetitive forces at work during routine activities on the Earth. Astronauts are instructed to execute resistance and endurance exercises for about two hours and day for six days a week in a combination of countermeasures against the effects of microgravity. The conflicting requirements of safe aerobic training with less intensive loads on leg joints must be satisfied under lengthy exposure to microgravity. Creating appropriate experimental approaches on the Earth and under microgravity and hypogravity is very challenging.

Although the effects of exercise on the human body have been investigated using mostly experimental approaches, advanced modeling and simulation techniques could be powerful tools for gaining insight into issues such as human physical limitations, forces at joints and forces generated by contracting muscles and the optimal conditions for training or exercise. Such techniques will help to quantitatively and qualitatively predict the effects of exercise under conditions of altered gravity. The present study used ergometer exercise models with the AnyBody Modeling System (AMS) ver. 6.0.6 (AnyBody Technology A/S, Aalborg, Denmark).

Oxygen uptake and loading on leg joints during ergometer exercise have only been examined experimentally. The present study aimed to validate an ergometer exercise model over a wide range of conditions to estimate oxygen uptake and reaction forces at leg joints and vertebral bodies by comparing the outcomes with experimental results, to develop a strategy for electrically stimulating antagonist muscles of joint motion to modulate oxygen uptake and joint loading under altered gravity, and to determine optimal conditions to satisfy conflicting requirements. A hybrid training system (HTS) that combines the electrical stimulation and volitional contraction of antagonist and agonist muscles, respectively, is an effective type of training [4] even for upper limbs under microgravity [5]. Co-contractile motions in the HTS can counteract the reduced effect of the gravitational force on leg joints during ergometer exercise.

2. Simulation Models for Ergometer Exercise

The musculoskeletal model in the AMS replicates a 50th percentile European male with a mass of 75 kg and a height of 1.76 m, respectively [6]. We modified the muscle activity function and muscle strength of “BikeModel” [7] in the AnyBody Managed Model Repository (AMMR ver.1.6.3) to construct a conventional ergometer (CER) exercise model with the HTS and reduced muscle strength. A seated model was constructed from the “StandingModel” based on the “BikeModel” and “LegPressMachine” in the AMMR ver.1.6.3 for recumbent ergometer (RER) exercise. Figure 1 shows both models that can simulate cycling with electrical stimulation of muscles around the leg joints based on the HTS concept and reduced muscle strength to represent weakened muscles. External forces and moments were applied to the thorax to maintain upper body posture while cycling on the CER model, even though the model lacks arms. In the RER model, a constant force of 56 N was applied to both anterior superior iliac spines to fix the pelvis on the seat of the ergometer. Friction forces (static friction coefficient of 0.6) between the surfaces of the backrest and the thoracic region, and between the gluteus region and the seat were also assumed instead of external forces and moments at the thorax. Thus, a person using the RER could exercise even at a gravitational acceleration < 1 g (9.81 m/s²) on the Earth. The relative positions of the hip joint and crank axis of the RER were determined to mimic that of the CER. The ankle plantar angle on the RER was obtained experimentally from our recumbent ergometer cycling with a position mimicking that of CER exercise at a pedal rate of 60 rpm and a mechanical load of 60 W. The leg joint angles of both models became similar (Figure 2). A crank torque on the pedal of the RER has a phase shift of quarter cycle of a crank torque on that of the CER.

The amount of oxygen uptake during exercise on the models can be derived from the caloric equivalent of oxygen [8] required for muscle power. The simulation results included oxygen uptake of 3.5 ml/kg/min at rest only when compared with the experimental results that were plotted with reference to regression equations derived from the literature.

Recruitment patterns in a redundant muscle system such as the human body are produced based on optimal methods to minimize an objective function and they consist of the ratio of muscle force to maximal muscle force; that is, muscle activity. The AnyBody system offers min/max criteria for muscle recruitment [9]: the largest endurance for a task or identical activation of all muscles contributes positively to balancing external force, thus minimizing maximal muscle activity as much as possible when muscles work together. This would be a

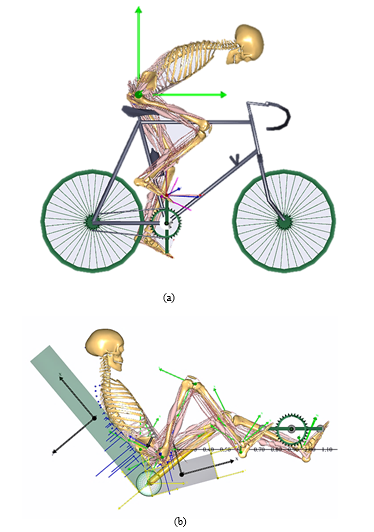Figure 1. Simulation models for ergometer cycling with hybrid training system (HTS) and reduced muscle strength. (a) Conventional ergometer (CER) from “BikeModel” in the AnyBody Managed Model Repository (AMMR ver.1.6.3). (b) Recumbent ergometer (RER) constructed from CER with backrest angle of 130° and seat tilt of 15°.

physiological criterion for minimal fatigue [10]. We combined the quadratic term of muscle activity with the objective function. A Hill-type muscle model [11] was adopted for the leg of the exercise model.

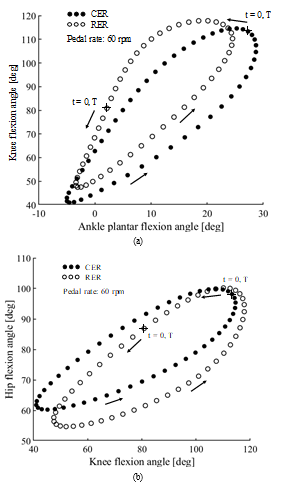Figure 2. Comparisons of leg joint angles between conventional ergometer (CER) and recumbent ergometer (RER) exercise at pedal rate of 60 rpm. (a) Ankle plantar flexion vs. knee flexion. (b) Knee flexion vs. hip flexion. T, pedaling duration. At time 0, the right foot is located at highest point.

3. Validation of Ergometer Exercise Models

Volitional CER (VCER) and volitional RER (VRER) exercise models were validated based on comparisons with experimental results on the Earth. The saddle height and position were set to 0.78 m superior and 0.17 m posterior from the crank axis on the VCER. The center of the hip joint was positioned 0.77 m posterior and 0.15 m inferior from the crank axis on the VRER. The length of both cranks was 0.17 m. The effect of the HTS combined with the CER (HCER) was also investigated.

3.1.  VCER Exercise at 1 g

The pedal rate and mechanical load of the VCER exercise model were varied with expanded experimental ranges. Figure 3 and 4 show oxygen uptake (ml/kg/min) at a pedal rate of 60 rpm under variable mechanical loads, and at defined mechanical loads of 81.7 and 0 W under different pedal rates, respectively. The simulation results shown in Figure 3 closely agreed with the experimental results [12] and increased linearly as mechanical load increased. The simulation results shown in Figure 4 were also similar to the experimental results [13,14] and increased

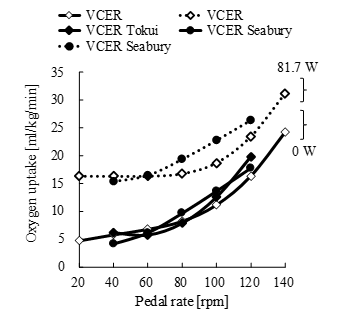Figure 4. Oxygen uptake during volitional conventional ergometer (VCER) exercise under various mechanical loads (0 and 81.7 W) and pedal rates. Unfilled and filled symbols indicate simulated and experimental results, respectively. Tokui and Seabury, oxygen uptake data from [13] and [14].

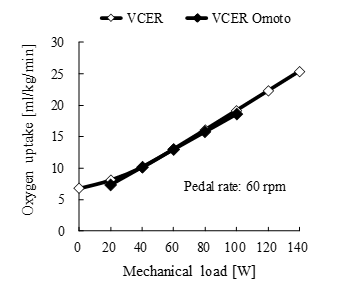Figure 3. Oxygen uptake during volitional conventional ergometer (VCER) exercise at a pedal rate of 60 rpm under various mechanical loads. Unfilled and filled symbols indicate simulated and experimental results, respectively. Omoto, oxygen uptake data from [12].

nonlinearly, showing quadratic curves as the pedal rate increased. Oxygen uptake will consistently increase beyond the upper limit of the experimental range.

The maximum magnitude of resultant forces at the knee joint during cycling has been measured using instrumented knee implants in elderly individuals who were free of pain and physically active after total knee replacement (TKR) [2]. We assumed 25% less muscle strength in the leg of the VCER exercise model with the muscle recruitment criterion of combined min/max and quadratic forms of muscle activity for comparisons with measured results. The simulated magnitude of the reaction force was reduced by approximately 10% of that using 100% muscle strength in the model. Moreover, the saddle height was set to 0.815 m, which mimicked the experimental conditions [2]. The simulated knee joint force closely agreed with the experimental findings of elderly individuals who engaged in ergometer exercise with an increasing mechanical load (Figure 5). The slow pedal rate resulted in a larger knee joint force. The increase in knee joint reaction force might be consistent with that above the experimental range.

The similar findings of these comparisons supported the validity and reliability of the ergometer exercise model except when values were beyond the lower limit of the experimental range. Little is known about ergometer exercise experiments at lower mechanical loads and pedal rates.

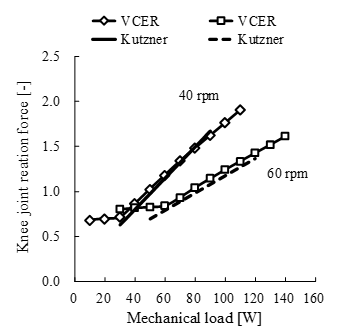Figure 5. Comparison of experimental and simulated results of knee joint reaction force during volitional conventional ergometer (VCER) exercise under various mechanical loads and pedal rates of 40 and 60 rpm. Reaction force is maximum magnitude of force normalized by body weight. Saddle height in simulation was set to 0.815 m to mimic experimental condition. Kutzner, joint reaction force data from [2].

3.2.  VRER Exercise at 1 g

Although both models had similar angles of leg joints, the upper body in the CER was dropped forwards and the body in the RER was inclined backwards (recumbent). Mean oxygen uptake at a pedal rate of 75 rpm in both positions was essentially identical at the same mechanical load [15]. Consumption tended to increase at higher loads in the recumbent position [15]. Simulated oxygen uptake in the VCER and VRER models was compared from the perspective of different mechanical loads and pedal rates (Figure 6.)

The difference in oxygen uptake between the two types of exercise rapidly increased as pedal rates increased, with oxygen uptake being higher for VRER, than VCER exercise. Further investigation is needed to validate the effect of RER exercise on the body.

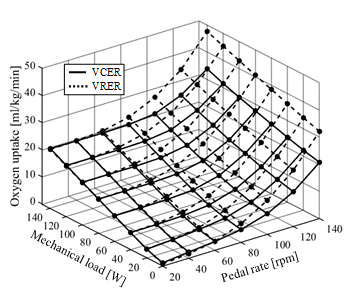Figure 6. Comparison of simulated oxygen uptake during volitional conventional (VCER) and recumbent (VRER) ergometer exercise under different mechanical loads and pedal rates. Solid and dotted lines indicate VCER and VRER exercise, respectively. More oxygen was consumed during VRER than VCER exercise. Both results increased linearly according to increasing mechanical load and nonlinearly according to increasing pedal rate.

3.3.  HCER Exercise at 1 g

The HTS was applied to the leg joints during ergometer exercise using the same leg motion as that used for volitional cycling. Stimulation intensities on the quadriceps femoris and hamstrings of the simulation model were determined at 1% and 5% of the maximum muscle activity, respectively, using the lower boundary of the muscle activity function in AnyBody. Stimulation that can fully activate assigned antagonist muscles at a specific intensity is ideal, unlike the actual situation during surface electrical stimulation (SES) [16-19]. The results of the simulation with low-intensity HTS closely agreed with the experimental findings of high-intensity SES (Figure 7). Additional effects of stimulation at intensities of 10%, 2% and 10% to the gastrocnemius, soleus, and tibialis anterior, respectively, were simulated to induce more oxygen uptake. At a pedal rate of 60 rpm (1-s cycle time), the antagonist muscles of the right knee during extension and flexion at the knee joint were stimulated for specific durations when knee angular velocities were > 2.0 and < –2.0 rad/s, respectively. These durations corresponded to 34% of the cycle time. The threshold of angular velocity of the plantar flexion angle of the right ankle was set to 1.0 rad/s, the corresponding duration of which was 26% of the cycle duration. The onset of stimulation on the left knee and ankle joints shifted half a cycle. The stimulus durations at all pedal rates were kept constant by adjusting the angular velocity setpoint according to the rate.

The increased oxygen uptake in the HCER was caused mainly by muscle co-contraction at the knee and ankle joints. The HCER linearly increased oxygen uptake, and the additional stimulation of muscles at the ankle joint similarly increased oxygen uptake. The increase in oxygen uptake with the HTS shows that the HCER can achieve the same exercise intensity as the VCER at higher mechanical loads.

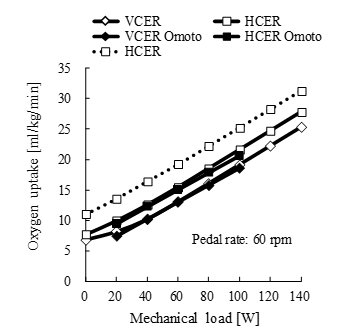Figure 7. Comparison of simulated and experimental results of oxygen uptake during volitional conventional ergometer (VCER) exercise and hybrid training system (HTS) combined with conventional ergometer (HCER) exercise under different mechanical loads at pedal rate of 60 rpm. Solid line, HTS acting on knee joint; dotted line, HTS acting on ankle and knee joints. Unfilled and filled symbols indicate simulated and experimental results, respectively. Omoto, oxygen uptake data from [12].

4. Prediction Under Altered Gravity

The simulation and experimental results at the acceleration of gravity on the Earth closely agreed. The effects of different accelerations of gravity, such as microgravity in spaceships and hypogravity on the surfaces of Mars and the Moon, on the human body must be considered for safe space exploration, maintaining health under altered gravity, and returning smoothly to activities of daily life (ADL) on the Earth. Good agreement will support various predictions under altered gravity.

4.1.  Oxygen Uptake During VCER and VRER Exercise Under Altered Gravity

The amounts of oxygen uptake at 0 g under mechanical loads of 60 and 120 W were essentially identical for each exercise. As gravity increased, oxygen consumption assumed a concave form during VCER exercise and a moderately concave form at both loads during VRER exercise. Although oxygen uptake varied, but the difference remained the same independently of gravity [20]. The lower oxygen uptake for the VCER and VRER ranged from 0.7 to 1.2 g and was dependent to some degree on mechanical load (Figure 8). The range of moderate gravity seemed to play assistive and resistive roles in the opposite leg for efficient oxygen consumption. Oxygen uptake during VCER exercise under varying gravitational acceleration became more concave than that while on the VRER. This might have been due to the different structure between the VCER and VRER; namely, the coordination of muscle activities of both legs is enhanced to maintain the pelvis position and steady cycling on the VCER under hypo- and hypergravity, respectively. In contrast, the backrest of the RER seat supports a reaction against the forward pushing force on the pedal of the VRER and restrained activities of lower limb muscles at hypergravity.

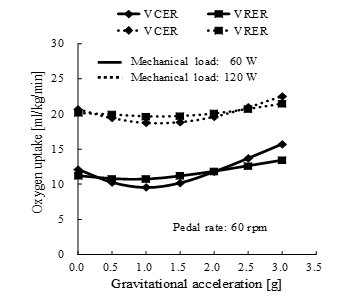Figure 8. Simulated oxygen uptake under mechanical loads of 60 and 120 W and altered gravitational acceleration during volitional conventional ergometer (VCER) exercise and volitional recumbent ergometer (VRER) exercise. g, acceleration of gravity on the Earth; 1 g = 9.81 m/s². Pedal rate, 60 rpm.

4.2.  Oxygen Uptake and Joint Reaction Force During VCER and VRER Exercise at 0 g

Oxygen uptake and the maximum magnitude of leg joint reaction forces that were normalized by body weight in the model, increased linearly with increasing mechanical load during VCER (Figure 9) and VRER exercise (Figure 10). Oxygen uptake and joint reaction forces at the knee and hip joints during VCER exercise were larger overall at 0 g (dotted lines) compared with those at 1 g (solid lines). Knee reaction force during VRER exercise was larger overall at 0 g than at 1 g, and oxygen uptake slightly increased with moderate variations under altered gravity.

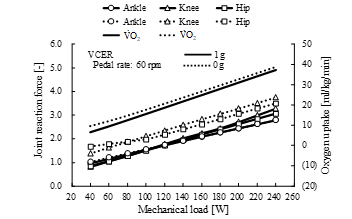Figure 9. Comparison of joint reaction forces and oxygen uptake between 1 g (solid line) and 0 g (dotted line) during volitional conventional ergometer (VCER) exercise at pedal rate of 60 rpm. Joint reaction force is maximum magnitude of force normalized by body weight. V̇O₂, oxygen uptake.

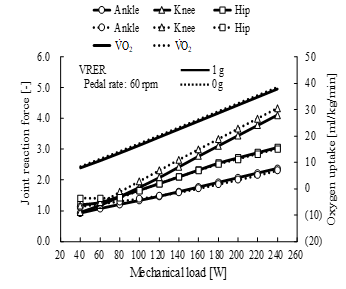Figure 10. Comparison of joint reaction forces and oxygen uptake between 1 g (solid line) and 0 g (dotted line) during volitional recumbent ergometer (VRER) exercise at pedal rate of 60 rpm. Joint reaction force is maximum magnitude of force normalized by body weight. V̇O₂, oxygen uptake.

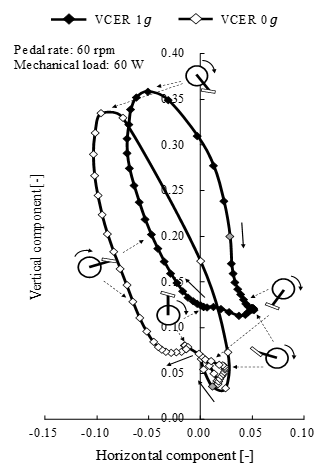Figure 11. Comparison of pedal reaction forces between 1 g (filled symbols) and 0 g (unfilled symbols) during volitional conventional ergometer (VCER) exercise at a pedal rate of 60 rpm and mechanical load of 60 W. Pedal reaction force is shown in horizontal and vertical components, normalized by body weight. Gray symbol, lowest point of pedal.

4.3.  Compensatory Actions During VCER Exercise at 0 g

The vertical component of the pedal reaction force became reduced and the horizontal component increased at 0 g (Figure 11), and the resultant pedal reaction force was lower than that at 1 g. The simulated force perpendicular to the crank (effective force) in the sagittal plane during VCER exercise was lower at 0 g with a pedal rate of 60 rpm and a mechanical load of 60 W than that at 1 g (Figure 12).

Muscles in the leg are activated to compensate for gravitational loss (Figure 13). Muscle force and joint reaction forces increase at 0 g and the increase in oxygen uptake was enhanced. The compensatory actions were smaller in the VRER than in the VCER, but the trends were similar.

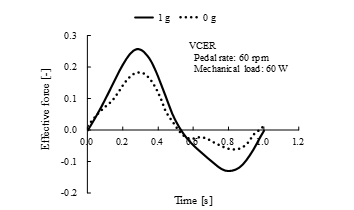Figure 12. Comparison of effective force between 1 g (solid line) and 0 g (dotted line) during volitional recumbent ergometer (VCER) exercise at pedal rate of 60 rpm and mechanical load of 60 W. Effective force perpendicular to crank, normalized by body weight.

4.4.  Effect of HTS on Ergometer Exercise at 0 g

Figure 14 shows the simulation results of oxygen uptake and knee joint reaction force during HCER exercise at 0 g with a mechanical load and two pedal rates corresponding to the experiment shown in Figure 5 at 1 g. The stimulation intensity was 10% and 20% of the maximum muscle activity of the quadriceps femoris and hamstrings, respectively. The oxygen uptake during VCER at 0 g varied linearly and increased at a pedal rate of 60 rpm.

Oxygen uptake under HTS will varylinearly with the same increment at mechanical loads that exceed the upper limit of the experimental range (similar to what is shown in Figure 9 for the VCER). The maximum magnitude of knee joint reaction forces during HCER exercise was over 3-fold body weight, which was much larger than the experimental and simulation results within the range of the mechanical load shown in Figure 15.

We confirmed the effects of the HTS on the reaction forces at leg joints over the mechanical load range of the experiment (Figure 15). The quadriceps femoris and hamstrings were stimulated at the same intensity as that shown in Figure 14. The maximum magnitude of resultant reaction forces induced at the knee and hip joints were ≥ 3-fold body weight and equivalent at least to the maximum at a mechanical load of 200 W during VCER exercise at 0 g (Figure 9). The maximum reaction forces at the leg joints at 40 rpm were essentially larger than those at 60 rpm.

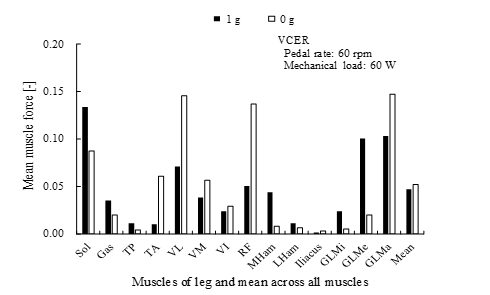Figure 13. Comparison of mean forces of leg muscles between 1 g (filled bars) and 0 g (unfilled bars) during volitional conventional ergometer (VCER) exercise at pedal rate of 60 rpm and mechanical load of 60 W. Force is averaged during one cycle, normalized by body weight. Mean, average of mean muscle force of leg at 0 g and became larger than that at 1 g. Abbreviations: Gas, gastrocnemius; GLMa, gluteus medius; GLMe, gluteus medius; GLMi, gluteus minimus; LHam, lateral hamstrings; MHam, medial hamstrings; RF, rectus femoris; Sol, soleus; TA, tibialis anterior; TP, tibialis posterior; VI, vastus intermedius; VL, vastus lateralis; VM, vastus medialis.

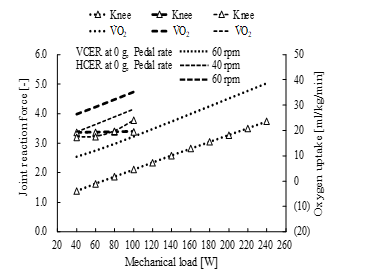Figure 14. Comparison of knee joint reaction force and oxygen uptake at 0 g during volitional conventional ergometer (VCER) exercise and hybrid training system (HTS) combined with conventional ergometer (HCER) exercise under various mechanical loads and pedal rates of 40 and 60 rpm. Joint reaction force is maximum magnitude of force normalized by body weight. V̇O₂, oxygen uptake.

4.5.  Optimal Cycling Conditions for CER exercise at 0 g

The HTS increased the amount of oxygen uptake and knee joint reaction forces. The simulated results of oxygen uptake and knee joint reaction force during VCER and HCER exercise at 0 g were comprehensively compared under various mechanical loads and pedal rates (Figures 16 and 17, respectively). The amount of variation in the incremental pedal rate was contradictory. The quadriceps femoris and hamstrings of the HCER model were stimulated at intensities of 10% and 20% of the maximum muscle activity, respectively.

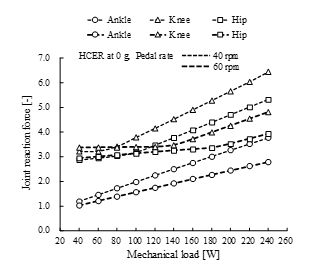Figure 15. Comparison of joint reaction forces at 0 g during hybrid training system (HTS) combined with conventional ergometer (HCER) exercise under different mechanical loads and pedal rates of 40 and 60 rpm. Joint reaction force is maximum magnitude of force normalized by body weight.

Astronauts will be recommended to exercise using an ergometer at selected intensities and knee joint reaction forces to maintain health under microgravity. The ergometer cycling conditions required to satisfy a specific exercise intensity and knee joint force could be determined from the conflicting features shown in Figures 16 and 17.

The optimal cycling conditions of mechanical load and pedal rate required to achieve a specific intensity and knee joint reaction force can be determined by minimizing the objective function, f (1). Table 1 shows the calculated optimal values for VCER and HCER exercise at 0 g. The reaction force was normalized by the body weight of the model.

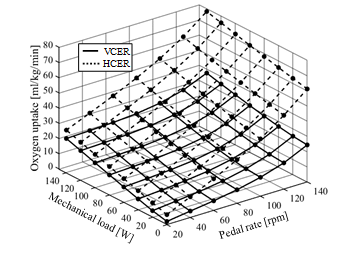Figure 16. Simulated results of oxygen uptake at 0 g during volitional conventional ergometer (VCER) exercise and the hybrid training system (HTS) combined with conventional ergometer (HCER) exercise under various mechanical loads and pedal rates. Solid and dotted lines, VCER and HCER exercise, respectively. More oxygen was consumed during HCER than VCER exercise.

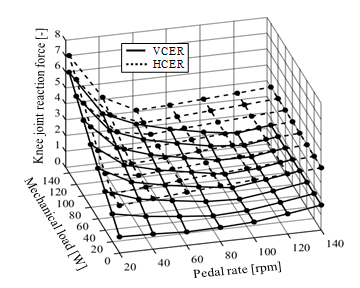Figure 17. Simulated results of knee joint reaction at 0 g during volitional conventional ergometer (VCER) exercise and the hybrid training system (HTS) combined with conventional ergometer (HCER) exercise under various mechanical loads and pedal rates. Solid and dotted lines, VCER and HCER exercise, respectively. Knee joint reaction force is greater at lower pedal rate and greater mechanical load in both exercises. Joint reaction force is maximum magnitude of force normalized by body weight.

The mechanical load for optimal cycling conditions in the HCER was half of that in the VCER, and the pedal rate was reduced by at least 17%. Minimizing the objective function for the VCER gave the desired values. The realized values of knee joint reaction force in the HCER increased by a maximum of 13% because the minimal value was 3-fold body weight at 20 rpm and 0 W.

Table 1.  Optimal cycling conditions for VCER and HCER at 0 g

Model Optimal cycling conditions Desired / realized values Mechanical load [W] Pedal rate [rpm] Oxygen uptake [ml/kg/min] Reaction force at knee joint [-] VCER 120 42.5 20/20 3.0/3.0 HCER 54.9 35.2 20/20 3.0/3.2 VCER 182 61.7 30/30 3.0/3.0 HCER 92.7 48.0 30/30 3.0/3.3 VCER 243 77.7 40/40 3.0/3.0 HCER 133 59.6 40/40 3.0/3.4 HCER, hybrid training system combined with conventional ergometer; VCER, volitional conventional ergometer

Figure 18. Human-ergometer system. System rotates about the Z axis of O-XYZ. O-XYZ, inertial frame; o-xyz, frame of human-ergometer system with origin at pelvis.

4.6.  Short Radius Artificial Gravity During RER Exercise at 0 g

Oxygen uptake and joint reaction forces were simulated by altering the rotational velocity of the RER model at 0 g, a pedal rate of 60 rpm and a mechanical load of 60 W (Figure 18). We assumed that the upper limb in this model reflected the force of artificial gravity at a fixed shoulder joint. The rotational axis Z was set to pass close to both ears. The RER rotated at a constant angular velocity at increments of 90 deg/s from 0 to 450 deg/s. The centrifugal acceleration of the origin of the human ergometer frame at each velocity (o-xyz), was 0, 0.16, 0.65, 1.45, 2.59, and 4.04 g. The HTS was introduced at the knee and ankle joints to increase oxygen uptake and joint reaction forces at the ankle, knee, and hip joints.

Figure 19 shows the maximum magnitude of resultant forces between adjacent vertebral bodies located below the 12th thoracic vertebra. The resultant forces were greater during the HTS combined with the RER (HRER) than VRER exercise at angular velocities of 0 and 90 deg/s. Both results increased quadratically with increases in the angular velocity of the human ergometer system, in which the respective artificial gravity of which was quadratically proportional to the angular velocity. The resultant forces between adjacent vertebral bodies remarkably increased with increasing artificial gravity to > 360 deg/s that generated a centrifugal acceleration of 2.59 g, and were close to the resultant forces that are generated when walking on a level surface [21].

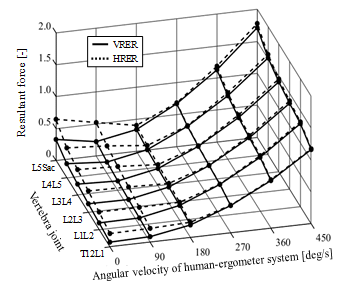Figure 19. Comparison of peak resultant forces between adjacent vertebral bodies during volitional recumbent ergometer (VRER) exercise and the hybrid training system combined with recumbent ergometer (HRER) exercise at 0 g, a pedal rate of 60 rpm and mechanical load of 60 W. Solid and dotted lines, VRER and HRER exercise, respectively. Reaction force is the maximum magnitude of the force, normalized by body weight. Stimulation intensity, 10%, 20%, 20%, 4% and 20% at quadriceps, hamstrings, gastrocnemius, soleus and tibialis anterior, respectively. L5Sac, between 5th lumbar spine and sacrum; LiLi+1, between ith and (i+1)th lumber vertebrae (i = 2,3,4); T12L1, between 12th thoracic and 1st lumbar vertebrae.

Figure 20 shows the effects of the HTS on the oxygen uptake and the maximal reaction force at each leg joint. The forces on the knee and hip joints during VRER exercise were not affected by the varied rotating velocity of the human ergometer system. The force on the ankle joint during VRER exercise was also not affected at rotating velocities < 180 deg/s, which rendered 0.65 g of centrifugal acceleration, while the force quadratically increased by > 180 deg/s. The HTS increased the oxygen uptake of 14 ml/kg/min at least and the joint reaction forces at the ankle, knee, and hip to 1.7-, 3.2-, 2.7-fold body weight, respectively. The soleus was activated to generate larger contraction forces at faster centrifugal acceleration to balance larger pedal reaction forces. These findings indicated that the HTS can enhance exercise intensity and joint reaction forces.

5. Discussion

Human in an environment with microgravity will experience disuse atrophy, resulting in the loss of mass and strength in muscles and bones. Exercise under such extreme circumstances has been examined and moderate exercise intensity has been implemented in spaceflight programs. Conventional ergometer cycling is a safe type of exercise that is easily implemented, because the exercise intensity can be controlled. Advanced modeling and simulation techniques are powerful tools that can provide insight into the physical limitations, optimal conditions, and mechanisms that might lead to muscle and joint damage instead of experimental approaches under extreme environments. Few studies have applied mathematical modeling and experimental approaches to determine joint reaction forces while walking [22] and oxygen uptake during ergometer exercise [20]

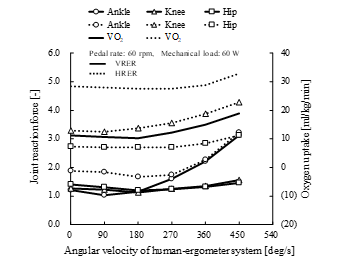Figure 20. Comparison of peak joint reaction forces and oxygen uptake during volitional recumbent ergometer (VRER) exercise and the hybrid training system combined with recumbent ergometer (HRER) exercise at 0 g, pedal rate of 60 rpm and mechanical load of 60 W. Solid and dotted lines, VRER and HRER exercise, respectively. Mean, average of mean leg muscle forces. Stimulation intensity, 10%, 20%, 20%, 4% and 20% at quadriceps, hamstrings, gastrocnemius, soleus and tibialis anterior, respectively. Joint reaction force is maximum magnitude of force, normalized by body weight.

under conditions of microgravity. Simulated reaction forces at hip joint under 100% body weight and a gravity replacement load of 80% imposed by spring-harnesses while walking in microgravity were approximately 3,000 N in the interior-superior direction [22]. Less oxygen uptake is simulated under cycling at 0 g than on the Earth [20]. The present study aimed to validate a cycling exercise model that included an HTS and reduced muscle strength for oxygen uptake and knee joint reaction force, by comparison with experimental results on the Earth, and to determine acceptable training conditions from case studies across a wide range of cycling parameters, including 0 g. Antagonist muscle activity is induced by electrical stimulation during movement in the HTS, and the principle agrees with the claim in [23] about training in space.

The cycling exercise model was constructed by modifying a commercially available bicycle model to simulate oxygen uptake during HTS cycling at 1 g and 0 g. The simulated oxygen uptake during VCER and HCER exercise at 1 g closely agreed with the experimental results described in [12] (Figure 7). Mean oxygen uptake at a pedal rate of 75 rpm in dropped forward and recumbent positions is essentially identical at the same mechanical load, but slightly increased at higher loads in the recumbent position [15]. Since we confirmed the same tendency in the VRER (Figure 6), several features of RER exercise predicted by simulation seemed acceptable. Oxygen uptake in hypergravity was lower during VRER than VCER exercise. This might have been due to the coordination of muscle activities in both legs being enhanced to maintain the steady crank rotation during VCER exercise, whereas reaction force generated from the back rest contributes to adjust the moment at the leg joints in the VRER. Consequently, the mean muscle forces of the legs in the VRER at hypergravity of 3 g became moderate and averaged far less than those in the VCER (Figure 21). Large muscle forces of the soleus (one-joint muscle across the ankle) were generated to balance the large pedal reaction forces at high gravitational and centrifugal acceleration.

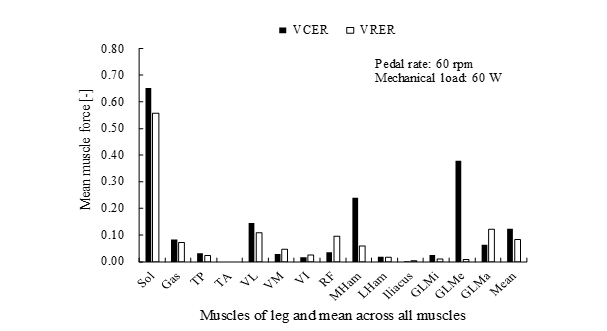Figure 21. Comparison of mean leg muscle forces during volitional conventional (VCER, filled bars) and volitional recumbent (VRER, unfilled bars) ergometer exercise at 3 g, a pedal rate of 60 rpm and mechanical load of 60 W. Force was averaged during one cycle, normalized by body weight. Abbreviations: Gas, gastrocnemius; GLMa, gluteus medius; GLMe, gluteus medius; GLMi, gluteus minimus; LHam, lateral hamstrings; MHam, medial hamstrings; RF, rectus femoris; Sol, soleus; TA, tibialis anterior; TP, tibialis posterior; VI, vastus intermedius; VL, vastus lateralis; VM, vastus medialis.

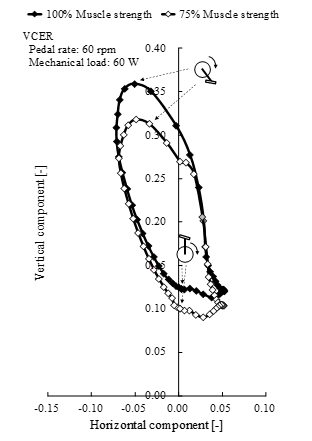Figure 22. Comparison of pedal reaction forces between 100% muscle strength (filled symbols) and 75% muscle strength (unfilled symbols) of volitional conventional ergometer (VCER) exercise at 1 g, a pedal rate of 60 rpm and mechanical load of 60 W. Joint reaction force is shown in horizontal and vertical components, normalized by body weight. Gray symbol, lowest pedal position.

The resultant pedal reaction force at 0 g was lower than that at 1 g (Figure 11). The effective force during VCER exercise with a pedal rate of 60 rpm and a mechanical load of 60 W was less at 0 g than at 1 g (Figure 12). The effective and resultant forces at 0 g will be decreased by compensatory actions of the loss of function due to zero gravity to maintain a specific pedal rate against an external mechanical load. Activated muscles in the leg at 0 g (Figure 13) are associated with such compensation. Effective and resultant forces decreased when elderly persons pedaled on the ground at 1 g compared with younger persons under the same cycling conditions [24]. Knee joint reaction

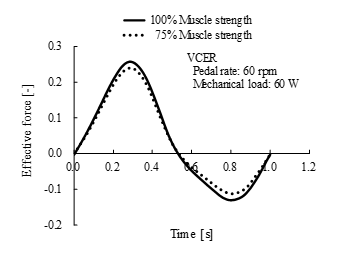Figure 23. Comparison of effective force between 100% muscle strength (solid line) and 75% muscle strength (dotted line) of volitional conventional ergometer (VCER) exercise at 1 g, a pedal rate of 60 rpm and mechanical load of 60 W. Joint reaction force normalized by body weight is shown in horizontal and vertical components.

forces in elderly individuals (n = 9; age, 62–76 years) during ergometer cycling 15 months after TKR were measured [2]. Simulated VCER exercise at 1 g with leg muscles weakened to mimic elderly persons after TKR agreed with their experimental findings (Figure 5). Moreover, we confirmed the same decreasing trend in the kinetics of pedal reaction force in VCER exercise at 1 g with weakened muscles of the leg (Figures 22 and 23). Comparisons between experimental and simulation results can indicate different compensatory actions between VCER with full muscle strength at 0 g and reduced muscle strength at 1 g.

From the perspective of physical adaptation, it is interesting that decreases in the magnitude of effective and resultant forces showed an identical trend during ergometer cycling by elderly persons at 1 g and healthy persons at 0 g. A loss of function in external factors such as a weightless environment should be compensated to realize the same motion on the Earth. The internal factor of weakened muscles will require elderly persons to choose different compensation methods, such as muscle coactivation [25].

A compressive load along the bone axis coupled with some high-force impulsive loading is generally required to maintain bone health. The following effects of repetitions per day for six weeks using an identical load on the ulna of mature turkeys were indicated [26]: a minimal number of repetitions is required to prevent bone loss, a greater number of repetitions is required to gradually increase bone formation, and even with an increase in the number of repetitions, there is a specific number of repetitions that shows no significant difference in bone formation. From a response relationship between peak strain magnitude and changes in ulnar bone mass in mature turkeys, the minimal effective strain to prevent bone loss was identified [27]. The effects of disuse, adaptation, mild overload and pathological overload on the strength of load-bearing bones were associated with the magnitude of strain [28]. The effects of both the number of repetitions and of the magnitude of joint reaction forces caused by muscle contraction force, external force, and virtual gravity on body elements must be considered under microgravity and hypogravity.

Astronauts are at high risk for bone fracture, especially during exposure to the stresses of re-entry into the atmosphere of the Earth after a long period of weightlessness [3]. Ergometer exercise can reduce the load imposed by gravitational force on the leg joints with a metabolic cost comparable to that of walking on the Earth [2]. This type of exercise is beneficial for persons with knee osteoarthritis and elderly individuals planning to engage in cardiovascular training but not for persons who are exposed to long periods of weightlessness. Fortunately, the HTS is compact, and should become a useful countermeasure to induce coactivated muscle activity during ergometer exercise. It allows repeated high loading on bones during long-term weightlessness (Figures 15, 17 and 20), which will elicit adaptive bone remodeling.

The great trochanter becomes highly deconditioned during long space flights [29]. Young males have undergone unilateral lower leg suspension (ULLS) for four weeks in a model of a weightless environment [30,31]. We conducted a ULLS experiment that included a healthy man with one foot completely weight-free, and a ULLS+HTS experiment involving four healthy men. The HTS electrical stimulation was applied to the quadriceps and hamstrings for 16 min three times a week while seated. Deconditioning of the hip at the femoral neck and greater trochanter was prevented. We confirmed the activities of the abductor, gluteus medius and minimus muscles attached to the greater trochanter using electromyography. Muscle activities of the gluteus medius and minimus muscles were simulated at 0 g and 1 g during VCER exercise (Figure 13), which elicited more activity of the vastus lateralis and rectus femoris of the knee extensor at 0 g than at 1 g, whereas the activity of the hip abductor at 0 g considerably decreased. Applying HTS stimulation to the quadriceps and the hamstring at intensities of 10% and 20%, respectively, recovered mean muscle forces induced by the gluteus minimus and medius 4.5- and 2.5-fold, respectively, compared with the absence of HTS stimulation at 0 g. Much larger loading will improve the reduced mineral density of the greater trochanter at 0 g.

Centrifugal acceleration is a physical phenomenon that might serve as an alternative to gravitational acceleration, and it is referred to as artificial gravity. Because the primary factor affecting physical deconditioning during spaceflight is the loss of gravitational loading and stimulation, the most effective physical countermeasure would be to introduce gravity [3]. Thus, artificial gravity generated by centrifugal acceleration has been studied. However, joint reaction forces in a rotating human-ergometer have not been analyzed from the viewpoint of preventing bone loss and reduced muscle strength. We examined oxygen uptake and joint reaction forces with altered rotational motion of the RER model while cycling at a pedal rate of 60 rpm and a mechanical load of 60 W (Figure 18). The resultant force on each vertebral body (Figure 19) at a rotating velocity > 360 deg/s was close to the results of walking on a level surface at 1 g [21], independently of the effects of HTS stimulation of the leg muscle. The eccentric force of the soleus at higher artificial gravity far exceeded the lower boundary force of the soleus induced by the HTS. The HTS affected the level of reaction forces at all leg joints whereas artificial gravity did not affect those at the knee and hip joints (Figure 20). Stimulation of the ankle joint increased oxygen uptake during HCER exercise at 1 g (Figure 7) as well as reaction force on the ankle joint (Figure 20). Intensive contractions of the gastrocnemius and the soleus muscles induced by the HTS will prevent the loss of bone density in the calcaneus.

An optimal method enabled the determination from conflicting characteristics, of the pedal rate and mechanical load during ergometer cycling that generates exercise intensity and loads on leg joints equivalent to those extant during daily physical activities on the Earth. Optimal cycling conditions were simulated to generate specific values for oxygen uptake and knee joint reaction force at 0 g under the constraints of using specific values for oxygen uptake as an index of aerobic and resistive exercise intensity, and of the knee-joint reaction force required to maintain bone mass and strength. The validity of the cycling exercise model with the HTS for oxygen uptake at 1 g was shown by comparisons between simulated and experimental results (Figure 7). The simulated optimal cycling conditions showed that muscle co-contraction during the HTS cycling under microgravity, which decreases both the pedal rate and mechanical load on the ergometer pedal (Table 1), can offer a strategy to decide the most effective training conditions derived from various combinations. This is an advantage for the operational demands of space vehicles or isolated bases located far from the Earth to maintain human health with time constraints and minimal environmental disruption.

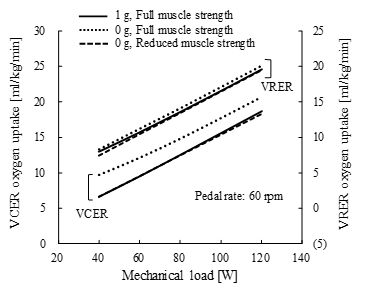Figure 24. Comparison of oxygen uptake at 1 g and 0 g between volitional conventional ergometer (VCER) and volitional recumbent ergometer (VRER) exercise at full and reduced muscle strengths under different mechanical loads. Representative deconditioning in simulation with reduced muscle strength was assumed for muscles opposing gravity effects, and the muscle recruitment criterion was changed for the decrease in oxygen uptake. Pedal rate, 60 rpm.

Less oxygen is uptaken under experimental microgravity than on the Earth [20], which reflects lower metabolic internal power. The experiment was repeated during a 180-day flight aboard the Mir station. Long-term exposure to weightlessness resulted in physiological deconditioning, and crews underwent repeated measurements under deconditioning. The oxygen uptake in Figure 9 was simulated under a healthy physical condition. To compare with the experiment under long-term exposure to microgravity, weakened muscle was assumed in the VCER and VRER models as follows.

The muscle strength of the leg muscles, psoas, erector and multifidi muscles was reduced to 65% of full strength, and the muscle recruitment criterion of the ergometer model was changed to the energy-related cost function proposed in [32]. Based on these assumptions, less oxygen was uptaken during VCER and VRER exercise at 0 g than that at 1 g (Figure 24), in which the mechanical load varied within the range of 40–120 W to beyond the experimental range [20]. This approach can evaluate reduced oxygen uptake by weakened muscles.

An oxygen uptake of 40 ml/kg/min in the simulation is approximately 84% of the mean maximal oxygen uptake in healthy adult males (age, 20-31 years) during ergometer exercise at 1 g [33]. Having 3-fold body weight in the simulated and desired reaction forces at the knee joint and the simulated reaction forces at the hip joint approximates the measured maximum magnitude of resultant forces at the knee joint during level walking in vivo at 1 g [34,35] and at the hip joint [35,36], respectively.

6. Conclusions

The validity of the ergometer exercise models was proven by comparisons with experimental findings. Model analysis provided perspectives even with widely varying parameters and altered exercise conditions. The HTS principle with exercise predicted an effective countermeasure to prevent deconditioning during lengthy exposure to microgravity. This approach will support future travel to Mars and will offer a benefit against hypogravity on the surfaces of the Moon and Mars. An optimal method could provide a better alternative to prevent deconditioning considering exercise intensity and loads on joints induced by daily activities at 1 g and operational demands in isolated equipment and facilities located far from the Earth.

This simulation was limited by the fixed leg angles and oxygen uptake, even under altered conditions of cycling and gravity. Leg angles during closed kinematic exercise such as cycling on an ergometer change according to age [24] and pedal rate [37]. The entire body including the cardiovascular and pulmonary systems undergoes deconditioning in microgravity [3], which alters the muscle fiber component ratio [38]. Open kinematic exercise such as knee and ankle joint flexion and extension does not require an ergometer or coordination between both legs during cycling. This exercise combined with the HTS will be simulated to confirm the amount of oxygen uptake and joint reaction forces. Changes in the ratio of the number of fast- to slow-twitch muscle fibers that are associated with oxygen uptake ability will be confirmed using the AMS, because these ratios increase under microgravity [38].

Conflict of Interest

The authors declare no conflict of interest.

Acknowledgments

This work was supported by JSPS KAKENHI Grant Numbers JP26506014, JP265006025.

1. Y. Tagawa, N. Yamamoto, M. Omoto, H. Matsuse, and N. Shiba, “Simulation of Oxygen Uptake and Leg Joint Reaction Force During Ergometer Exercise Under Altered Gravity,” in 39th Annual International Conference of IEEE EMBC, Jeju Island, Korea, 2017. DOI: 10.1109/EMBC.2017.8037219.
2. I. Kutzner, B. Heinlein, F. Graichen, A. Rohlmann, A.M.Halder, A. Beier, and G. Gergmann, “Loading of the knee joint during ergometer cycling: telemetric in vivo data,” J. Orthop. Sports Phys. Ther., 42(12), 1032-1038, 2012. DOI: 10.2519/jospt.2012.4001
3.  G. Clement and A. Bukley (Editors), Artificial Gravity, Microcosm Press and Springer, 2007.
4.  T. Yanagi, N. Shiba, T. Maeda, K. Iwasa, Y. Umezu, Y. Tagawa, S. Matsuo, T. Yamamoto, K. Nagata, and J.R. Basford, “Agonist contractions against electrically stimulated antagonists,” Arch. Phys. Med. Rehabil., 84(6), 843-848, 2003. DOI: 10.1016/S0003-9993(02)04948-1
5.  N. Shiba, H. Matsuse, Y. Takano, K. Yoshimitsu, M. Omoto, R. Hashida, Y. Tagawa, T. Inada, S. Yamada, and H. Ohshima, “Electrically stimulated antagonist muscle contraction increased muscle mass and bone mineral density of one astronaut – Initial verification on the International Space Station,” PLoS One, 10(8), 14 pages, 2015. DOI: 10.1371/journal.pone.0134736
6. T. Weber, A.A. Al-Munajjed, G.J. Verkerke, S. Dendorfer, and T. Renkawitz, “Influence of minimally invasive total hip replacement on hip reaction forces and their orientations,” J. Orthop. Res., 32(12), 1680-1687, 2014. DOI: 10.1002/jor.22710
7. Under Interface Features, Lesson 2-4, The AnyBody Modeling System version 6.0.6, AnyBody Tutorials, 2016.
8. E.T. Howley and B.D. Franks, Health Fitness Instructor’s Handbook, Human Kinetics, 1997.
9. J. Rasmussen, M. Damsgaard, and M. Voight, “Muscle recruitment by the min/max criterion –a comparative numerical study,” J. Biomech., 34(3), 409-415, 2001. DOI: 10.1016/S0021-9290(00)00191-3
10.  M. Damsgaard, J. Rasmussen, S. T. Christensen, E. Surma, and M. de Zee, “Analysis of musculosketetal systems in the AnyBody Modeling System,” Simul. Model Pract. Th., 14(8), 1100-1111, 2006. DOI: 10.1016/j.simpat.2006.09.001
11.  M.L. Ohlsson and M. Gulliksson, “Least squares approach to inverse problems in musculoskeletal biomechanics,” Technical report, Mid Sweden University, 10 pages, 2009.
12.  M. Omoto, H. Matsuse, Y. Takano, S. Yamada, H. Ohshima, Y. Tagawa, and N. Shiba, “Oxygen uptake during aerobic cycling exercise simultaneously combined with neuromuscular electrical stimulation of antagonist,” J. Nov. Physiother., 3(6), 185-191, 2013. DOI: 10.4172/2165-7025.1000185
13.  M. Tokui, “Analysis of the muscular mechanical efficiency focused on internal and external power,” Ph.D Thesis, Kyushu Institute of Technology, 2008, (in Japanese).
14. J.J. Seabury, A.C. Adams, and M.R. Ramey, “Influence of pedaling rate and power output on energy expenditure during bicycle ergometry,” Ergonomics, 20(5), 491-498, 1977. DOI: 10.1080/00140137708931658
15. H.I. Griffiths, “Comparison of energy expenditure among three different cycling positions,” Graduate Student These, Dissertations, & Professional Papers, University of Montana, 1989.
16.  Y. Tagawa and N. Yamamoto, “For improvement of motor function by surface electrical stimulation,” Special Issue, J. Inst. Elect. Engnr. Jpn., 136 (19), 666-669, 2016, (in Japanese).
17.  T. Watanabe, Y. Tagawa, E. Nagasue, and N. Shiba, “Surface electrical stimulation to realize task oriented hand motion,” in 31st Annual International Conference of the IEEE EMBS, Minneapolis, Minnesota, USA, 2009. DOI: 10.1109/IEMBS.2009.5333812
18.  T. Watanabe, Y. Tagawa, and N. Shiba, “Mapping method using a super multi-electrical stimulation device,” in 15th IFESS Annual Conference, Vienna, Austria, 2010.
19.  M. Gobbo, N.A. Maffiuletti, C. Orizio, and M.A. Minetto, “Muscle motor point identification is essential for optimizing neuromuscular electrical stimulation use,” J. NeuroEng. Rehabili., 11(6), 6 pages, 2014. DOI: 10.1186/1743-0003-11-17
20.  M. Girardis, D. Linnarsson, C. Moia, D.R. Pendergast, and G. Ferretti, “Oxygen cost of dynamic leg exercise on a cycle ergometer: effects of gravity acceleration,” Acta Physiol. Scand., 166(3), 239-246, 1999. DOI: 10.1046/j.1365-201x.1999.00564.x
21.  A. Rohlmann, M. Dreischarf, T. Zandr, F. Graichen, and G. Bergmann, “Loads on a vertebral body replacement during locomotion measured in vivo,” Gait & Posture, 39(2), 750-755, 2014. DOI: 10.1016/j.gaitpost.2013.10.010
22.  S. Dendorfer and S. Torholm, “Harness – walking in microgravity,” Final Report on Feasibility Study, Report no: 21385/08/NL/PA, AnyBody Technology A/S, 20-24, 2008.
23.  G.A. Dudley, P.A. Tesch, B.J. Miller, and P. Buchanan, “Importance of eccentric actions in performance adaptations to resistance training,” Aviat. Space Environ. Med., 62(6), 543-550, 1991.
24.  J.W. Seo, D.H. Kim, S.T. Yang, D.W. Kang, J.S. Choh, and G.R. Tack, “Comparison of joint kinematics and pedaling force in the young and the elderly,” J. Phys. Ther. Sci., 28(8), 2245-2248, 2016. DOI: 10.1589/jpts.28.2245
25.  Y. Tagawa, Y. Ogata, and N. Yamamoto, “Simulation of muscle activity during cycling with full and reduced muscle strengths of the leg,” in 39th Annual International Conference of IEEE EMBC, Poster, Jeju Island, Korea, 2017.
26.  C.T. Rubin and L.E. Lanyon, “Regulation of bone formation by applied dynamic loads,” J. Bone Joint Surg., 66-A(3), 397-402, 1984.
27.  C.T. Rubin and L.E. Lanyon, “Regulation of bone mass by mechanical strain magnitude,” Calcif. Tissue Int., 37(4), 411-417, 1985.
28.  H.M. Frost, “A 2003 update of bone physiology and wolff’s law for clinicians,” Angle Orthod., 74(1), pp.3-15, 2004. DOI: 10.1043/0003-3219(2004)074<0003:AUOBPA>2.0.CO;2
29.  M.R. Barratt and S.L. Pool (Editors), Principle of Clinical Medicine for Space Flight, Springer, 2008.
30.  T. Ito, Y. Tagawa, S. Tanaka, N. Shiba, Y. Umezu, T. Yamamoto, and J.R. Basford, “Development of practical and effective hybrid exercise for use in weightless environment,” in 26th Annual International Conference of the IEEE EMBS, San Francisco, USA, 2004. DOI: 10.1109/IEMBS.2004.1404185
31.  R. Takeuchi, Y. Tagawa, T. Inada, K. Suetsugu, K. Mimura, and N. Shiba, “A countermeasure for preventing atrophy of musculoskeletal system under microgravity,” in SICE-ICCAS 2006 SICE-ICASE International Joint Conference, Busan, Korea, 2006. DOI: 10.1109/SICE.2006.315451
32.  M. Praagman, E.K.J. Chawick, F.C.T. van der Helm, and H.E.J. Veeger, “The relationship between two different mechanical cost functions and muscle oxygen consumption,” J. Biomech., 39(4), 758-765, 2006. DOI: 10.1016/j.jbiomech.2004.11.034
33.  T. Matsuo, K. Ohkawara, S. Seino, N. Shimojo, S. Yamada, H. Ohshima, K. Tanaka, and C. Mukai, “An exercise protocol designed to control energy expenditure for long-term space missions,” Aviat. Space Environ. Med., 83(8), 783-789, 2012. DOI: 10.3357/ASEM.3298.2012
34.  I. Kutzner, B. Heinlein, F. Graichen, A. Bender, A. Rohlmann, A. Halder, A. Beier, and G. Bergmann, “Loading of the knee joint during activities of daily measured in vivo in five subjects,” J. Biomech., 43(11), 2164-2173, 2010. DOI: 10.1016/j.jbiomech.2010.03.046
35. P. Damm, I. Kutzner, G. Bergmann, A. Rohlmann, and H. Schmidt, “Comparison of in vivo measured loads in knee, hip and spinal implants during level walking,” J. Biomech., 51, 128-132, 2017. DOI: 10.1016/j.jbiomech.2016.11.060
36.  G. Bergmann, A. Bender, J. Dymke, G. Duda, and P. Damm, “Standardized loads acting in hip implants,” PloS One, 11(5), 23 pages, 2016. DOI: 10.1371/journal.pone.0155612
37.  R.R. Bini, M. Rossato, F. Diefenthaeler, F.P. Carpes, D.C. dos Reis, and A.R.P. Moro, “Pedaling cadence effects on joint mechanical work during cycling,” Isokinet. Exerc. Sci., 18(1), 7-13, 2010. DOI: 10.3233/IES-2010-0361
38.  V.R. Edgerton, M.Y. Zhou, Y. Ohira, H. Klitgaard, B. Jiang, G. Bell, B. Harris, B. Saltin, P.D. Gollnick, R.R. Roy, M.K. Day, and M. Greenisen, “Human fiber size and enzymatic properties after 5 and 11 days of spaceflight,” J. Appl. Physiol., 78(5), 1733-1739, 1995. DOI: 10.1152/jappl.1995.78.5.1733

(Click Here)

(Click Here)