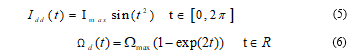1. Introduction

In the electric drives systems, more than 70% of produced electrical energy is converted into mechanical energy. Therefore, a high energy efficiency of electric drives systems is demanded [1-2]. PMSMs (Permanent Magnet Synchronous Motors) gain more attention in variable speed drives due to their good efficiency, fast torque response, high power density, cooling, and lack of maintenance.

 There are two types of PMSM: motors with surface mounted permanent magnets (SPMSM) and motors with internally mounted permanent magnets (IPMSM). The main difference between these two types is the existence of reluctant torque component which exists only in IPMSM due to the rotor salience [2]. The rotor of IPMSM has high mechanical strength and therefore this type of motor can operate in high speed drives [3-4].

Output tracking control has large applications in dynamic processes in industry, biology, and economics [5-6-7-8]. The most important objective of tracking control is to construct the output of the system, via a controller and track the output of a given reference model as close as possible [9].

In a PMSM system, there are wide quantities of the uncertainties and disturbances, unmodeled dynamics, friction force [10-11-12]. It will be very hard to limit these disturbances rapidly if adopting some classical control methods and also it is very difficult to solve the tracking control problem with these methods.

 To circumvent some afore mentioned problems, an NDIC (Nonlinear Dynamic Inversion Control) was introduced, in which limit these disturbances rapidly and this approach solve the tracking control problem [1-2-13]. NDIC has been used for the study of direct current and speed tracking in PMSM, through this method, simulation results were obtained and compared. A performance study of this control technique was proposed and developed and a new validity study namely “Validity Abacus” is proposed in this work.

The present paper falls into five sections. It unfolds with a section about the PMSM control and NDIC approach. Section 2 characterize a (d-q) mathematical model of PMSMs and proposed an implementation of NDIC approach of the direct current and the speed tracking control of PMSM. Section 3 introduces the frequency and amplitude dependent model. Simulation results are discussed and conclusions comments are given respectively in sections 4 and 5.

2. Preliminaries

In this section, some preliminaries are introduced, including PMSM (d-q) model and NDIC method, to propose a new tracking control approach.

2.1.  Proposed Model

The important things are the design of tracking control systems to realize the variation speed and high precision motion. The PMSM electrical equations can be written in the (d-q) rotor flux reference [14-15] as following:

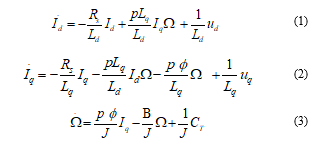I_d and I_q: d and q axis stator currents.

Ω: rotor speed.

U_d and U_q: d and q stator voltages

2.2.  NDIC Proposed Method

In this paper, the NDIC proposed approach will be used as a tracking controller for the direct current and the rotor speed of PMSMs to investigate its utility [1-16-17-18]. Figure 1 present the structure of the inverting law of the nonlinear dynamic inversion control approach.

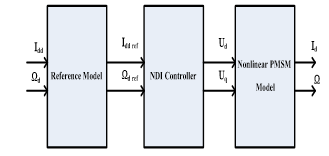Figure.1. Nonlinear Dynamic Inversion Control approach [1]

The control objective is to track a desired direct current (I_dd) and speed (Ω_d) with respectively the actual direct current (Id) and the rotor speed (Ω). The dynamic nonlinear model of the PMSM expressed in equations (1, 2 and 3) is taken in the following form: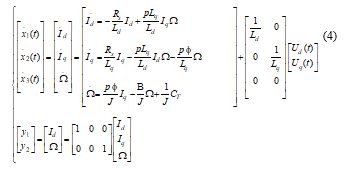

With:

 : is the state vector system

: is the input vector

: is the output vector

Using the nonlinear dynamic inversion proposed approach; the input can be obtained using the successive derived from the output. Then U_d(t) is expressed by equation 7.

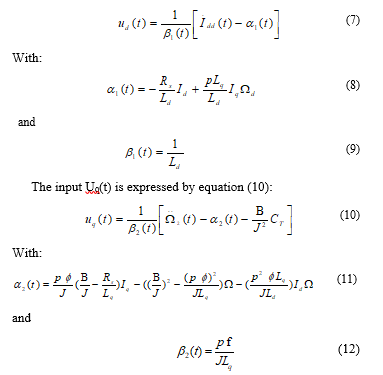3. Validity Abacus Approach

In order to validate the proposed nonlinear dynamic inversion approach, the following methodology is used in figure 2.

#first step: the mathematical nonlinear (d-q) model of PMSM is developed.

#Second step: this step consists in describing the frequency dependence of the speed tracking control model. In the third step, simulation results are compared to the desired model for both the direct current I_dd and the speed Ω_d.

# Third step: the errors between the desired data and the simulation results are computed. Based on these errors, discrepancies between them are depicted in order to finally judge on the correction of the model parameters. Figure 2 summarizes the previously presented steps respectively.

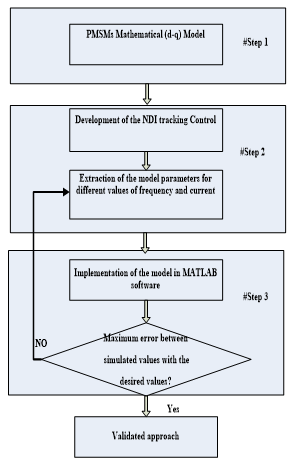Figure 2.Validity Abacus Methodology

Important to note, that the estimated errors between the desired outputs and the obtained ones, are in good agreements. This paper presents.

A novel to easy methodology to easy study performance of control methods by only optimization error between desired and simulated results for rotor speed and direct current at different frequency and amplitude levels. This methodology may be applied for others control approach.

Table 1: PMSM parameters and values [1]

Parameter	Denotation	Value
P	Pole pair number	2
Rs	Stator resistance	1.9 W
Ld	d-axis inductance	42.44 mH
Lq	q-axis inductance,	79.57 mH
f	Frequency	50 Hz
φf	Magnetic flux constant,	0.311 Wb
J	Inertia of the motor	0.003 kg.m2
CT	Motor torque	3.954 Nm
B	Friction coefficient	0.001 Nm/rad/s

4. Simulation Results

The rotor speed and direct current tracking control using NDIC approach and the frequency and amplitude dependent model of PMSM are emulated in MATLAB. Table I present the numerical parameters of the studied model.

Figure 3 and figure 4 shows the speed characteristics at different frequency levels respectively in low and high frequency. The different amplitude of the desired direct current (see figure 5) the change in the saturation speed.

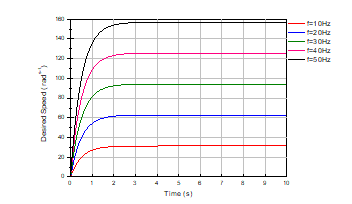Figure.3. Desired speed characteristics at different frequency (low- frequency f= [10 è50Hz]).

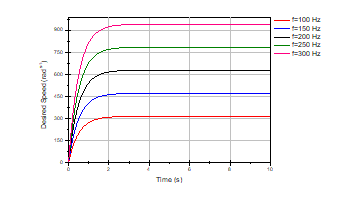Figure.4. Desired speed characteristics at different frequency (high- frequency f= [100 è300Hz]).

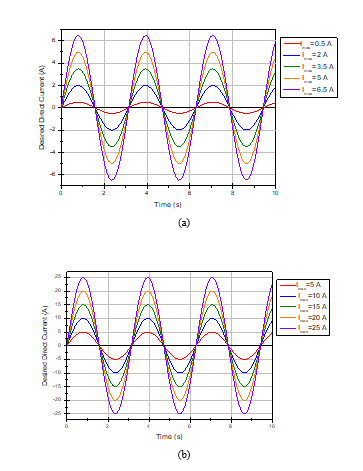Figure 5. Desired current characteristics at different amplitude

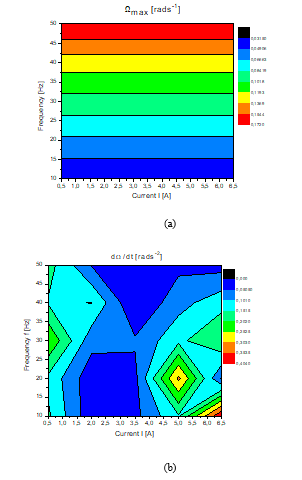Figure.6. Validity abacus of rotor speed tracking control in

 low- frequency: (a) Ω, (b) dΩ/dt

Figures 6 and 7 are an illustration of validity abacus of tracking parameter error (Ω, dΩ/dt). The rotor speed tracking of permanent magnet synchronous motor has been performed for different data both in low and high frequency. These latter, may be effective in the optimization of rotor speed tracking using a nonlinear dynamic inversion control approach. Then, these abacuses evaluate the accuracy of simulation results.

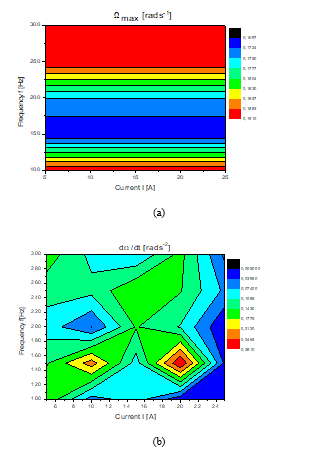Figure.7. Validity abacus of speed tracking control in high-frequency

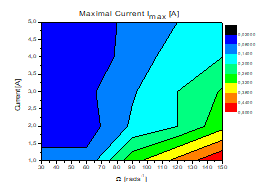Figure 8. Validity abacus of direct current for rotor speed

[30 rad/s à150rad/s]

The Ω abacus (Figure 6.a and 7.a) illustrates that the nonlinear dynamic inversion control approach of the rotor speed tracking PMSM parameters offers a wide range of validity. The error between the estimated maximal speed rotor Ω_d and the obtained simulation is less than 0.2% for different rotor speed level in low and high frequency. The dΩ/dt validity abacus shows an error less than 0.5% at low and high frequency (Figure 6.b and 7.b). The I_d abacus (Figure 8) illustrate that NDIC of the direct current tracking offer a wide range of validity. The error between the estimated maximal direct current I_dd and the obtained simulation get by this approach is less than 1% for different current level for both the proposed PMSM.

The error is mainly due to the nonlinearity of PMSM model equations. Parameters error is less than 0.5% for different conditions. The obtained result proves the effectiveness of the control to ensure a rotor speed and direct current tracking. The abacus also helps the engineer to evaluate the simulation results accuracy of given devices. Various upshots and diverse validity abacus are satisfying so far. For a low and high frequency conditions, the proposed methodology is then adequate. Moreover, this model offers an efficient trade-off between ease and accuracy of speed tracking control study.

However, simulation errors cannot be avoided. They are calculated according to the rotor speed and the direct current at different frequency and amplitude. An error less than 0.5% is found for the permanent magnet synchronous motor model proposed. In addition to its precision, the suggested model has got a good convergence. Furthermore, the ease of use is one more advantage. It consists in both the facility of implementation using MATLAB and the simplicity in extracting PMSM model parameters. Moreover, the proposed algorithm, integrating the developed model, allows a better detection and adjustment of the outputs tracking control (using NDIC approach). In fact, in the case of poor design, the model replies routinely by detecting and tuning it. Nonlinear dynamic problems are, therefore, methodically avoided.

5. Conclusion

In this paper we have demonstrated that the PMSMs have the direct current and the rotor speed proportional to the frequency and amplitude. A mathematical nonlinear model of this motor is also proposed. The novel of this model is that it takes into account the design structure as well as frequency and amplitude parameters. The model validation is performed by comparing desired results with simulation. This model is run for a large range frequency and amplitude, and the simulation investigations show a good agreement with respect to the desired ones. These results are validated and. Future works concern the validation of the NDIC proposed approach associate the “Abacus Validity” approach others nonlinear systems.

1. S. Jebri , K. Nouri and L. Bouslimi,” Study Performance of Speed Tracking Control with Frequency an Amplitude Dependence”IC_ASET, IEEE conferences Tunisia, Janvier 2017.
2.  S. Jebri ; H. Loussifi ; K. Nouri,” Two Mass Modeling and Nonlinear Dynamic Inversion of Motor Drive Systems”. Sciences and Techniques of Automatic Control and Computer Engineering, IEEE conf . July 2016.
3.  J. Hu, D. Dawson, and Y. Qian, “Position tracking control of an inductionmotor via partial state-feedback,” Automatica, vol. 31, pp. 989–1000, 1995.
4.  D. M. Dawson, Z. Qu, and J. J. Carroll, “Tracking control of rigid-link electrically-driven robot manipulators,” Int. J. Control, vol. 56, no. 5, pp. 991–1006, 1992.
5.  Z. Qu and J. Dorsey, “Robust tracking control of robots by a linear feedback law,” IEEE Trans. Autom. Control, vol. 36, no. 9, pp. 1081–1084, Sep. 1991.
6.  L. Benvenuti, M. D. Di Benedetto, and J. W. Grizzle, “Approximate output tracking for nonlinear nonminimum phase systems with an application to flight control,” Int. J. Robust Nonlinear Control, vol. 4, no. 3, pp. 397–414, 1994.
7.  F. Liao, J. L. Wang, and G. H. Yang, “Reliable robust flight tracking control: An LMI approach,” IEEE Trans. Control Syst. Technol., vol. 10, no. 1, pp. 76–89, Jan. 2002.
8.  N. C. Shieh, P. C. Tung, and C. L. Lin, “Robust output tracking control of a linear brushless DC motor with time-varying disturbances,” Inst. Elect. Eng. Proc. Elect. Power Appl., vol. 149, no. 1, pp. 39–45, 2002.
9.  G. Bartolini, A. Ferrara, and E. Usai, “Output tracking control of uncertain nonlinear second-order systems,” Automatica, vol. 33, no. 12, pp. 2203– 2212, 1997.
10.  X. Chen and C.-Y. Su, “Robust output tracking control for the systems with uncertainties,” Int. J. Syst. Sci., vol. 33, no. 4, pp. 247–257, 2002.
11.  P. Seiler and R. Sengupta, “An H∞ approach to networked control,” IEEE Trans. Autom. Control, vol. 50, no. 3, pp. 356–364, Mar. 2005.
12.  N. C. Shieh, K. Liang, and C. Mao, “Robust output tracking control of an uncertain linear system via a modified optimal linear-quadratic method,” J. Optim. Theory Appl., vol. 117, no. 3, pp. 649–659, 2003.
13.  D.Yang and J. Zhao,” H1 output tracking control for a class of switched LPV systems and its application to an aero-engine model” .International Journal of Robust and Nonlinear Control, September 2016.
14.  Y.Xin Li and G.Hong Yang,” Fuzzy Adaptive Output Feedback Fault-Tolerant Tracking Control of a Class of Uncertain Nonlinear Systems With Nonaffine Nonlinear Faults”IEEE Transactions on Fuzzy Systems .Vol.24, no: 1, Feb. 2016.
15.  B.A. Francis and W.M. “Wonham. The internal model principle of control theory”. Automatica, 12(5–E):457–465, 1976.
16.  M. Koç, J. Wang, T. Sun,” An Inverter Nonlinearity Independent Flux Observer for Direct Torque Controlled High Performance Interior Permanent Magnet Brushless AC Drives” IEEE Trans. Power Electron, Volume:PP , Issue: 99, February 2016.
17.  T. D. Do, S. Kwak, H. H. Choi, and J. W. Jung, “Suboptimal control scheme design for interior permanent magnet synchronous motors: An SDRE-based approach,” IEEE Trans. Power Electron., vol. 29, no. 6, pp. 3020–3031, Jun. 2014.
18.  K. Nouri, R. Dhaouadi, and N. B. Braiek, “A dynamic neural network based decoupled extended Kalman filter control applying to motor drive system,” 17ème Congrés Mondial IMACS, Calcul Scientifique, Mathématique Appliquées et Simulation, 2005

(Click Here)

(Click Here)