1. Introduction

Communications among individual or organizations are increasing day by day. Everyone wants to keep their private information secure from any type of threats or being lost. Cryptography achieves this goal to secure private information. Schemes are being developed rapidly and frequently for cryptography and attacks on those schemes are being developed often too. New attacks are being strong, effective and attenuating the security of existing cryptographic schemes.

Rijndael block cipher was proposed as AES by September 03, 1999 [1]. National Institute of Standards and Technology (NIST) announced Rijndael block cipher as AES by Federal Information Processing Standards Publication 197 (FIPS 197) by November 26, 2001. Several attacks were developed after the publication of AES that are threatening for AES but not practically successful on full AES. Until 2006, the best-known attacks were on 7 rounds, 8 rounds, and 9 rounds for 128-bit keys, 192-bit keys, and 256-bit keys respectively [2]. However, in the recent time, many attacks are close to successful on AES. For the reduced 8-round version of AES-128, the first known-key distinguishing attack was released as a preprint in November 2009 [3]. It works with a memory complexity of 2³², and a time complexity of 2⁴⁸. In 2011 [4], the first key-recovery attack on full AES was developed. This biclique attack is four times faster than the brute force attack. It requires 2^126.2, 2^190.2 and 2^254.6 operations to recover an AES-128, AES-192 and AES-256 key respectively. This result has been further improved to 2^126.0, 2^189.9 and 2^254.3 operations for AES-128, AES-192 and AES-256 key respectively [5], which are the current best results in key recovery attack against AES.

As intended to develop AES with extended key sizes for more security against recently developed attacks by keeping the performance almost similar to that of AES. Thus proposed algorithm becomes more complex for Interpolation attack, Basic attack, and Square attack. Differential and Linear cryptanalysis will be inefficient for this algorithm too. Since this algorithm uses two different keys derived from one key, it will be more complex and impossible to crack in spite of having known plaintext-ciphertext pairs available. The throughput of the proposed algorithm is nearly similar to that of AES. It is shown that for a 100KB text file, encryption time taken by AES-128 is 0.100s where for EAES-256 it is the same amount of time.  Performances of other versions of EAES are evaluated and they are effective too.

The rest of the paper is organized as follows: Section 2 briefly explain related research works, Section 3 describes the proposed EAES algorithm, Section 4 shows the performance analysis of EAES, Section 5 describes the strength of EAES against different types of attacks and Finally, Section 6 concludes the paper.

2. Background

After the proposal of AES encryption by Rijndael, a large number of research works has been done on it. An FPGA based architecture for a new version of 512-Bit Advanced Encryption Standard algorithm design and evaluation was proposed in [6]. It (AES-512) uses both input and key block size of 512-bits which makes it more resistant to cryptanalysis against the break of its security. Throughput increased by 230% when compared with the implementation of the original AES-128. But requires more control logic blocks (CLBs) in implementation prospect than existing AES.

An efficient parallel implementation and optimization of the Advanced Encryption Standard (AES) algorithm based on the Sunway TaihuLight was proposed in [7]. The Sunway TaihuLight is a China’s independently developed heterogeneous supercomputer [8] with peak performance over 100 Petaflops. Specifically, they expanded the scale to 1024 nodes and achieved the throughput of about 63.91 GB/s (511.28 Gbits/s). But with the increase of input data the throughput grows from quick to slow pattern.

A new efficient and novel approach to protect AES against differential power analysis was proposed in 2015 [9]. The implementation of this approach provides a significant improvement in strength against differential power analysis with a minimal additional hardware overhead. The efficiency of their proposed technique was verified by practical results obtained from real implementation on a Xilinx Spartan-II FPGA.

In 2016, an implementation of AES algorithm to overt fake keys against counter attacks was proposed [10]. An approach to overt the cryptographic key, when there is any counter attacks so-called side-channel attacks (SCAs) are applied in order to break the security of AES-128. Experimental results make sure the strength of the proposed approach to successfully hide the true cryptographic key. But it is more time consumptive than existing AES.

Constructing key dependent dynamic S-box for AES block cipher system was proposed in 2016 [11]. A new approach to generating dynamic S-box which was constructed centered on round key. Predefined static S-boxes pose a weak point for the attackers to analyze certain ciphertext pairs. The new S-boxes created were additionally dynamic, random and key dependent which attempts to escalate the complexity of the algorithm and furthermore mark the cryptanalysis more challenging. However, the performance in terms of time and power consumption is not examined and showed in this paper.

An implementation of AES-128 and AES-512 on
Apple mobile processor [12] was proposed in 2017 that uses 512 bits of data block size using key sizes of 128, 192, 256, 512 and 1024 bits. However, again the performance degrades with the extension of key lengths.

3. Proposed Extended AES (EAES)

Advanced Encryption Standard (AES) is the most used and most secure algorithm at present among other symmetric cipher algorithms. But recently some sorts of attack such as biclique attack are threatening for AES. AES uses key sizes of 128 bits, 192 bits and 256 bits [13]. The authors have developed an algorithm almost similar to AES with some exceptions and double in key sizes (i.e., key sizes of 256, 384 and 512 bits) and highly secure than AES.

The proposed EAES algorithm has four parts: encryption, decryption, key division and key expansion. It takes plaintext block length of 128 bits as the existing AES. Every encryption and decryption process goes through several numbers of rounds according to their key sizes. This algorithm is named depending on its key lengths as EAES-256, EAES-384, and EAES- 512. Key sizes with corresponding round numbers are given in Table 1.

Table 1. Key sizes with corresponding round numbers of the cipher

Key Size ( bits/bytes/words )	Round Number ( Nr )
256/32/8	10
384/48/12	12
512/64/16	14

3.1.  Key Division

This part of the algorithm takes a cipher key and divides it into two equal sub-keys in a simple way. The resulting two sub-keys are named FirstKey and SecondKey. Size of both sub-keys can be 128, 192 and 256 bits since the cipher key can be 256, 384 and 512 bits. FirstKey has byte values that are in odd positions in the cipher key and SecondKey has byte values that are in even positions in the cipher key. Figure 1 shows an example of this key division process where each letter is identified as a byte and the cipher key is 256 bits or 32 bytes.

Figure 1 Key division example of the cipher key expansion

Two different key expansions are used for two sub-keys. Since sub-key sizes are 128, 192 and 256 bits for cipher key sizes of 256, 384 and 512 bits respectively, the values of  for both sub-keys will be same as defined in AES. Sub-key expansions can be described as follows:

1. At first, the sub-key is copied into the first words of the array of expanded sub-key. In other words, the first  words of the expanded sub-key are filled with the sub-key which is also  words long.
2. Words in positions that are a multiple of go through a more complex function which is denoted by .
3. Every following word w[i] is equal to the XOR of the previous word w[i – 1] and the word position earlier w[i – ]. Note that i starts with 1, not 0.
4. The complex function takes a single word or 4 bytes as input then passes it through the following three subsequent operations:
   1. RotWord: If the sub-key is FirstKey, it performs a one-byte circular left shift on a word. This means an input word [B₁, B₂, B_3, B₄] transformed into [B₂, B₃, B_4, B₁]. If the sub-key is SecondKey, it performs a one-byte circular right shift on a word. This means an input word [B₁, B₂, B_3, B₄] transformed into [B₄, B₁, B_2, B₃].
   2. SubWord: It performs a byte substitution on each byte of its input word using the S-box used for AES.
   3. The result of operation b is XORed with a round constant Rcon[i]. The round constant is a word in which the first byte is different for different round values but the rightmost three bytes always remain constant. Round Constants are different for FirstKey and SecondKey. Rcon[i] values for FirstKey and SecondKey expansions are given in Table 2. For FirstKey expansion, the rightmost three bytes of the Round Constant are always 0. Rcon[i] = (RC[i], 0, 0, 0) with RC[1] = 1, RC[i] = 2 RC[i – 1]. For SecondKey expansion, among the right most three bytes of the Round Constant, the first and third bytes are equal to hexadecimal value  that means all bits of these two bytes are 1. The second byte is equal to {00} that means all bits of the second byte are 0. Rcon[i] = (RC[i], , 0, ) with RC[1] = 1, RC[i] = 3 · RC[i – 1] = [2 Å 1] · RC[i – 1] = (2 · RC[i – 1]) Å RC[i – 1]. The symbol “ · ” denotes multiplication over the field . The values of RC[i] in hexadecimal form are shown below where the value of “i” denotes round number.
5. If and (i – 4) is a multiple of  then SubWord is applied to w[i – 1] prior to the XOR.

Table 2. Rcon[i] values for FirstKey and SecondKey expansion

i	1	2	3	4	5	6	7	8	9	10	11	12	13	14
RC[i] (for FirstKey)	01	02	04	08	10	20	40	80	1B	36	6C	D8	AB	4D
RC[i] (for SecondKey)	01	03	05	0F	11	33	55	FF	1A	2E	72	96	A1	F8

Two different complex functions  used in the expansions of FirstKey and SecondKey are shown in Figure 2.

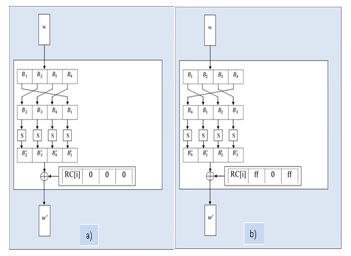Figure 2 Complex function g for a) FirstKey expansion and b) SecondKey expansion

After successful expansion of the FirstKey and SecondKey, each of the expanded FirstKey and SecondKey has a total of   words. From these, every four words were used for each round. The expanded FirstKey and SecondKey of  words are shown in Figure 3.

Figure 3 Expanded a) FirstKey and b) SecondKey

3.2.  Encryption or Cipher

The encryption process takes the plaintext input into the state and passes it through a single stage at the beginning of the cipher named AddFirstRoundKey. Then the state passed through  rounds to get the expected ciphertext as output. Each of first  rounds has five consecutive stages that are: SubBytes, AddSecondRoundKey, ShiftRows, MixColumns, and AddFirstRoundKey. The last round that means ^th round has all four stages except the MixColumns stage. Figure 6 shows full encryption process with all  rounds.

3.2.1 SubBytes, ShiftRows and MixColumns Transformation

These stages do the exact similar transformations as AES.

3.2.2 AddFirstRoundKey Transformation

In this stage, an -word FirstRoundKey is added to the state by simple bitwise XOR operation. A FirstRoundKey is  words length as the state. The FirstRoundKey is provided from the FirstKey expansion function that expands the  words FirstKey into  words expanded FirstKey. This addition could be described as a column-wise addition of the state matrix and the FirstRoundKey. The following figure shows the addition of a column of four bytes of the state and a word of the FirstRoundKey, where i indicates the value . The lowest value of  is zero which indicates the first AddRoundKey stage without round and the highest value is the last round number. Figure 4 shows the AddFirstRoundKey transformation.

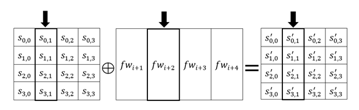Figure 4 Addition between FirstRoundKey and state

3.2.3 AddSecondRoundKey Transformation

In this stage, a -word SecondRoundKey is added to the state by simple bitwise XOR operation as like AddFirstRoundKey stage but the only exception is that first  words of the expanded SecondKey are not added to the state. Figure 5 shows the AddSecondRoundKey transformation.

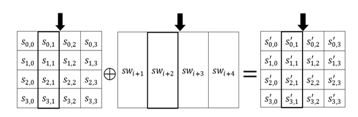Figure 5 Addition between SecondRoundKey and state

Encryption and decryption process of proposed algorithm are shown in Figure 6.

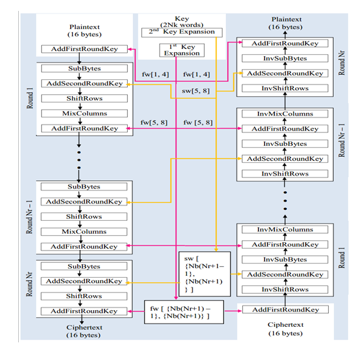Figure 6 Full round encryption and decryption process of proposed EAES algorithm

3.3.  Decryption or Inverse Cipher

Decryption process takes the ciphertext input into the state and passes it through a single stage at the beginning of the inverse cipher named AddFirstRoundKey. Then the state passed through  rounds to get the expected plaintext as output. Each of first  rounds has five consecutive stages that are: InvShiftRows, AddSecondRoundKey, InvSubBytes, AddFirstRoundKey and InvMixColumns. The last round that means ^th round contains all four stages except the InvMixColumns stage. Figure 6 shows the total decryption process.

3.3.1 InvShiftRows, InvSubBytes and InvMixColumns Transformation

These stages do the same transformations as AES.

3.3.2 AddFirstRoundKey and AddSecondRoundKey Transformation

These two stages perform the similar operation as described for encryption process except that they add the expanded round keys to the state from the end of the expanded key.

4. Performance Analysis

Before the performance comparison of the proposed EAES and original AES, AES algorithms were tested with the input-output vector combination provided by National Institute of Standards and Technology (NIST) [14]. Then times taken by AES and the proposed algorithm for encryption and decryption of different fixed plaintext sizes with their different key lengths were measured. The authors used a system of the configurations listed in Table 3 to test both of AES and proposed EAES algorithm.

Table 3. System configuration used for performance measurement

Device Name	Company: Acer, Model: Aspire 4749z (Laptop)
CPU Clock Rate	2.20 GHz, 2200MHz
RAM Size	4.00 GB
Hard Drive Size	1.00 TB
Processor Name	Intel(R) Pentium(R) CPU B960 @ 2 Core(s)
Processor Generation	2nd Generation
Operating System	Microsoft Windows 10 pro, Version: 10.0.10586  Build 10586.
Compiler	Name: Code::Blocks, Type: GNU GCC
Programming Language used	C
Plaintext and Ciphertext File Type	.txt

Two plaintext files (i.e., .txt) were taken for performance measurements. Sizes of chosen files are 100KB and 200KB. The encryption and decryption process was done for three times and then the time averaged. Table 4 shows the time taken for AES and the proposed EAES algorithm with different key size to encrypt and decrypt 100KB text file.

The time comparison between AES-128 and EAES-256; AES-192 and EAES-384; AES-256 and EAES-512 shows that encryption and decryption times are almost same between AES and EAES for 100KB text file. However, EAES versions are nearly some milliseconds slower than existing AES.

Table 4. Time taken to encrypt and decrypt 100KB text file

Alg.	AES-128		AES-192		AES-256		EAES-256		EAES-384		EAES-512
Time(s)	Enc.	Dec.	Enc.	Dec.	Enc.	Dec.	Enc.	Dec.	Enc.	Dec.	Enc.	Dec.
	0.069	0.278	0.069	0.332	0.084	0.393	0.062	0.285	0.062	0.354	0.084	0.401
	0.053	0.285	0.069	0.332	0.069	0.400	0.062	0.285	0.069	0.352	0.069	0.416
	0.053	0.279	0.053	0.332	0.079	0.384	0.052	0.285	0.062	0.354	0.084	0.401
Average Time(s)	0.058	0.280	0.064	0.332	0.077	0.392	0.059	0.285	0.064	0.353	0.079	0.406

Table 5. Time taken to encrypt and decrypt 200KB text file

Alg	AES-128		AES-192		AES-256		EAES-256		EAES-384		EAES-512
Time(s)	Enc.	Dec.	Enc.	Dec.	Enc.	Dec.	Enc.	Dec.	Enc.	Dec.	Enc.	Dec.
	0.100	0.554	0.147	0.670	0.132	0.791	0.100	0.599	0.115	0.707	0.147	0.809
	0.100	0.577	0.100	0.693	0.138	0.793	0.100	0.601	0.122	0.707	0.138	0.817
	0.084	0.583	0.122	0.664	0.131	0.791	0.100	0.602	0.125	0.702	0.131	0.822
Average Time(s)	0.095	0.571	0.123	0.676	0.134	0.792	0.100	0.600	0.120	0.705	0.139	0.816

Table 5 compares the time taken between AES-128 and EAES-256; AES-192 and EAES-384; AES-256 and EAES-512; and again shows that encryption and decryption times are almost same between AES and EAES for 200KB text file while EAES versions are some milliseconds slower than AES. Moreover, for a 200KB text file, the encryption and decryption time is clearly greater than the time taken for 100KB text file for all versions of AES and EAES as expected. Parallel Execution of AES-CTR Algorithm Using Extended Block Size [15] was proposed in 2011 that can be used to increase the performance of real-time uses of proposed EAES.

5. Strength of Proposed EAES Algorithm

The number of alternative keys and times taken by the brute-force attack to get the original cipher key are listed in Table 6. The authors have proposed an approach [16] that uses genetic algorithm and neural network in S-box. This feature can also be used to increase the security of proposed EAES.

Table 6. Average time required for exhaustive key search

Key Size (bits)	Number of Alternative keys	Time Required at 109 Decryption/Sec	Time Required at 1013 Decryption/Sec
256	2256» 1.2 × 1077	2255 ns = 1.8 × 1060 years	1.8 × 1056 years
384	2384» 3.9 × 10115	2383 ns = 6.2 × 1098 years	6.2 × 1094 years
512	2512» 1.34× 1077	2511 ns = 2.1 × 10137 years	2.1 × 10133 years

5.1 Strength Against Different Attacks

     Several cryptanalysis attacks such as linear attack, algebraic attack, SAT-solver and hybrid attack, Side channel attack, distinguishing and related-keys attack revised in [17] and are very important for AES. EAES increases algorithm complexity and security against those attacks.

5.1.1 Biclique Attack

Still now, the best publicly known single-key attack on AES is biclique attack. It uses a computational complexity of 2^126.1, 2^189.7 and 2^254.4 for AES-128, AES-192, and AES-256 respectively. It is the only publicly known single-key attack on AES that attacks the full number of rounds. Previous attacks have attacked round reduced variants (typically variants reduced to 7 or 8 rounds). This attack is only theoretical but not practical because it’s high complexity as mentioned above. But it describes many safety margins of AES such as round numbers and key sizes. The proposed algorithm uses higher key sizes that are two times larger than AES which ensures more security for this type attack.

5.1.2 The Basic Attack

The authors placed a new stage between SubBytes and ShiftRows so that the algorithm becomes obsolete to basic attack. The scheme used for the basic attack will not be applicable for this algorithm. This extra stage of key addition ensures the nonlinearity of this algorithm.

5.1.3 The Square Attack

The “Square” attack utilizes the byte-oriented structure of Square cipher and is a dedicated attack on Square. This attack is also valid for AES, as AES inherits many properties from Square. The attack is independent of the multiplication polynomial of MixColumns, the key schedule and the specific choice of SubBytes and is also known as a chosen plaintext attack. It is faster than an exhaustive key search for AES versions of up to 6 rounds. However, no attacks faster than exhaustive key search have been found for 7 rounds or more. The proposed algorithm uses two different key schedules and two addition of cipher key that ensures high diffusion. So it ensures extra security to this algorithm.

5.1.4 Related-key Attacks

In this type of attacks, using a chosen relation, the cryptanalyst can do cipher operations with different unknown or partly unknown keys. The high diffusion and non-linearity key schedule of AES makes it very inviolable for this attack. The proposed algorithm uses two different key schedules with the same complexity as AES that ensures higher security than AES for this type of attack.

6. Conclusion

Security of this algorithm is higher than any other symmetric ciphers at present. In real life this algorithm can be implemented and used in applications like smart phone apps, real-time multimedia communication, and private network communications, SSL communications, ATMs etc with increased security than existing AES. The proposed algorithm is implemented using C programming language and then tested it with some plaintext blocks. It can also be easily implemented by other high level languages like C++, JAVA, C#, Python etc. The performance results are shown and compared with AES.  Time consumptions were approximately same as AES but the security was higher than AES. This algorithm has just been developed, implemented and tested for performance analysis. The complexity and security of this algorithm have been evaluated theoretically. It is found that this algorithm is more secure than AES. But it is essential to analyze the result of the algorithm for various practical attacks. That defines the future works of the proposed algorithm.

1. J. Daemen and V. Rijmen, “AES Proposal: Rijndael” in: Proc. first AES conference, 1998.
2. N. Ferguson, J. Kelsey, S. Lucks, B. Schneier, M. Stay, D. Wagner, D. Whiting, “Improved Cryptanalysis of Rijndael” Fast Software Encryption Lecture Notes in Computer Science, 213-230, 2001. https://doi.org/doi:10.1007/3-540-44706-7_15
3. H. Gilbert, T. Peyrin, “Super-Sbox Cryptanalysis: Improved Attacks for AES-Like Permutations” Fast Software Encryption Lecture Notes in Computer Science, 365-383, 2010. https://doi.org/doi:10.1007/978-3-642-13858-4_21
4. A. Bogdanov, D. Khovratovich, C. Rechberger, “Biclique Cryptanalysis of the Full AES” Lecture Notes in Computer Science Advances in Cryptology – ASIACRYPT 2011, 344-371, 2011. https://doi.org/doi:10.1007/978-3-642-25385-0_19
5. B. Tao, H. Wu, “Improving the Biclique Cryptanalysis of AES” Information Security and Privacy Lecture Notes in Computer Science, 39-56, 2015. https://doi.org/doi:10.1007/978-3-319-19962-7_3
6. A. Mohd, Y. Jararweh, L. Tawalbeh, “AES-512: 512-bit Advanced Encryption Standard algorithm design and evaluation” 7th International Conference on Information Assurance and Security (IAS), 2011. https://doi.org/doi:10.1109/isias.2011.6122835
7. Y. Chen, K. Li, X. Fei, Z. Quan, K. Li, “Implementation and Optimization of AES Algorithm on the Sunway TaihuLight” 17th International Conference on Parallel and Distributed Computing, Applications and Technologies (PDCAT), 2016. https://doi.org/doi:10.1109/pdcat.2016.062
8. “Sunway TaihuLight” – Wikipedia. (n.d.). Retrieved March 24, 2018, from https://en.wikipedia.org/wiki/Sunway_TaihuLight
9. M.Masoumi, M. H. Rezayati, “Novel Approach to Protect Advanced Encryption Standard Algorithm Implementation Against Differential Electromagnetic and Power Analysis” IEEE Transactions on Information Forensics and Security, 10(2), 256-265, 2015. https://doi.org/doi:10.1109/tifs.2014.2371237
10. S.Savitha, S. Yamuna, “Implementation of AES algorithm to overt fake keys against counter attacks” International Conference on Computer Communication and Informatics (ICCCI), 2016. https://doi.org/doi:10.1109/iccci.2016.7480017
11. G.Manjula, H. S. Mohan, “Constructing key dependent dynamic S-Box for AES block cipher system” 2nd International Conference on Applied and Theoretical Computing and Communication Technology (iCATccT), 2016. https://doi.org/doi:10.1109/icatcct.2016.7912073
12. S.Vatchara, K. Piromsopa, “An Implementation of AES-128 and AES-512 on Apple Mobile Processor” 14th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), 2017. https://doi.org/doi:10.1109/ ecticon.2017.8096255
13. “Advanced encryption standard (AES)” 2001. https://doi.org/doi:10.6028/nist.fips.197
14. M.J. Dworkin, “Recommendation for block cipher modes of operation” 2001. https://doi.org/doi:10.6028/nist.sp.800-38a
15. NTran, M. Lee, S. hong, S. Lee, “Parallel Execution of AES-CTR Algorithm Using Extended Block Size” 14th IEEE International Conference on Computational Science and Engineering, 2011. https://doi.org/doi:10.1109/cse.2011.43
16. K.Kalaiselvi, A. Kumar, “Enhanced AES Cryptosystem by Using Genetic Algorithm and Neural Network in S-Box” IEEE International Conference on Current Trends in Advanced Computing (ICCTAC), 2016, https://doi.org/doi:10.1109/icctac.2016.7567340
17. D.M. Alghazzawi, S. H. Hasan, M. S. Trigui, “Advanced Encryption Standard – Cryptanalysis Research” International Conference on Computing for Sustainable Global Development (INDIACom), 2014, https://doi.org/doi:10.1109/indiacom.2014.6828045

(Click Here)

(Click Here)