1. Introduction

Hydrogen is the lightest of gases and possesses the lowest density. However at ambient temperature and pressure it occupies a large volume, a car, whose weekly need is on average 5 Kg of hydrogen, must have a spherical tank of radius r # 2.44 m. This necessitates compressing it at high pressures up to P # 800 Bars [1]. The immense interest generated by hydrogen comes from the fact that it has the best energy per weight ratio of all fuels and the ecological nature of the combustion product (water vapor). But much of the energy is lost during storage. From the pedagogical point of view, it is also the most taught and involved in research. In particular in quantum mechanics, this deals with the state of particles such as the electron. This aspect is treated in this article in order to solve the problem of storage of the hydrogen by minimizing losses as much as possible. The solutions envisaged are, first, the improvement of the theory to understand the physical phenomena that occur in the physical system, especially the resolution of the transcendental equation, and then the means of perfecting the materials constituting the cavity (tank).

The confinement of atoms or molecules in a finite region of space is an important subject, for example, in the context of quantum dots, encapsulation in fullerenes, or other aspects of nanotechnology. Confinement in a cavity has also been used to simulate the effects of high pressure. A hydrogen atom at the center of a spherical cavity was first studied by Michels & al. in 1937 [2] in order to model hydrogen at high pressure, as well as by Sommerfeld and Welker in 1938 [3], and also in an extended body of subsequent work [4, 5, 6, 7].

Most of these works use the standard Dirichlet boundary condition with a vanishing wave function at the cavity wall, while some use Neumann boundary conditions, i.e. a vanishing gradient of the wave function perpendicular to the wall. A notable exception is where the most general so called Robin boundary condition has been considered [8].

Al-Hashimi in a recent article 2012 [9], has well studied the problem of hydrogen which is confined in a spherical cavity using the conditions at the limits of Robin, he also introduced a transcendental equation for the calculation of the energies.

However to solve theoretically, hydrogen gas transmission phenomenon that is enclosed in a spherical cavity or into a conical cavity and under high pressure, two equations are necessary: the Schrödinger equation, equation (1), which is well known and, the Victor Gustave Robin boundary condition equation (2)

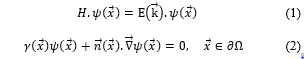The self-adjoint extension parameter      takes   into account   the constituent material of the cavity,  is the wave function, ∂Ω is the limit of a spatial region Ω and  is the unit vector perpendicular to the surface. As usual, the wave function can be factored as the product of a radial function  with a spherical harmonic function  according to the following expression

This equation is difficult to solve because of the size, effectively the radial function is graphically traceable in 2D graph, and the spherical harmonic function in 3D dimension. And thus the product, ie the wave function, is of dimension greater than or equal to four.

2. Theory of spherical harmonics

The spherical harmonic functions are defined either as the eigenfunctions of angular momentum in quantum physics, or as the solutions of the Laplace equation  [10, 11, 12, 13]. Solving this equation in spherical coordinates leads to the following expressions [14]:

where   is the Legendre associated polynomial of degree       and order m

and  is the normalization function:

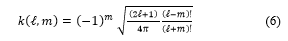2.1.  Expressions of the spherical harmonics

The terms of spherical harmonics which have azimuthally quantum numbers  = 1,  = 2 and  = 3 are defined, in quantum mechanics, as follows:

: Necessarily implies that the magnetic quantum number is zero (m=0).

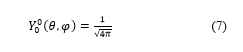 There are three possible values for m: m = 1, m = 0 and m = -1.

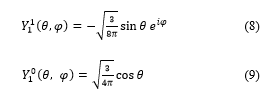
 There are five possible values for m: m = 2, m = 1, m = 0, m = -1 and m = -2.

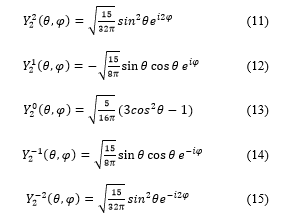 There are seven possible values for the magnetic quantum number m: m = 3, m = 2, m = 1, m = 0, m = -1, m = -2 and m = -3.

3. Theory of the radial functions

As a preparation for the hydrogen problem, in this section we consider a ‘‘free’’ particle in a spherical cavity with general   reflecting   boundary    conditions specified by the self-adjoint extension parameter . And after that, we study the problem of the hydrogen atom in a spherical cavity with general reflecting boundary conditions, again specified by the self-adjoint extension parameter  (real numbers).

3.1.  Particle in a spherical cavity with general reflecting boundaries

Let us consider the Hamiltonian of a free particle of mass M in spherical coordinates:

with angular momentum  in a spherical cavity of radius R. As usual, the wave function can be factorized as:

where the angular dependence is described by the spherical harmonics . For , the radial wave function obeys to:

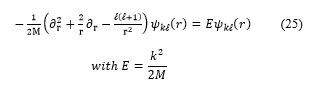For a spherical cavity, the most general perfectly reflecting boundary condition of equation (2) takes the form:

For positive energy the normalizable wave function is given by the spherical Bessel functions:

For general  at γ = −  /R, the ground state has zero energy with the radial wave function given by:

Consider the following cases:

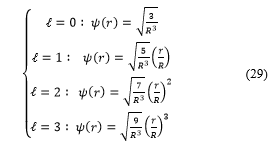3.2.  Hydrogen atom in a spherical cavity with general reflecting boundaries

In this section consider an electron bound to a proton that is localized at the center of a spherical cavity with general reflecting boundary conditions, again specified by the self-adjoint extension parameter    . The Hamiltonian radial equation of the hydrogen atom, in spherical coordinates, takes the expression:

and the normalizable wave function is given by:

where  is an associated Laguerre function [15] and [16], and a is the Bohr radius and A is a constant.

Consider the following cases:

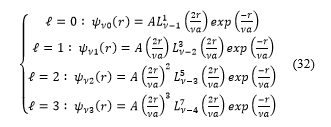And for  , expressions (32) take the form :

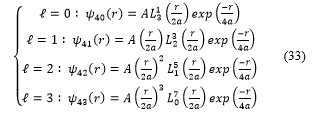4. Implementation and graphs of the spherical harmonics functions [17]

The graphs of spherical harmonic functions, calculated above, were modeled and mapped with “SPharm” program Matlab environment 7.8.0 (R2009a). The essential functions are plotted on figure (1) and figure (2) below:

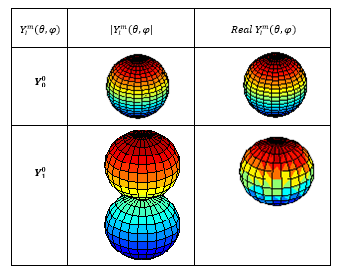Figure (1): The module and the real part of the

spherical harmonic functions:

4.1.  Graphs of the radial functions and the density functions for the hydrogen atom

Knowing the associated Laguerre functions expressions:

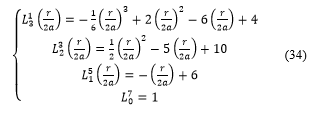
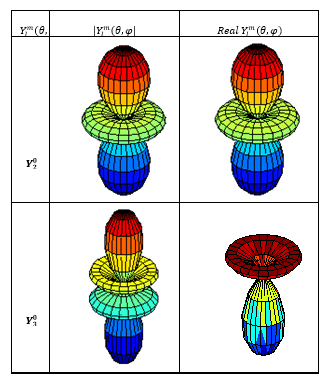Figure (2): The module and the real part of the spherical harmonic functions:

The radial functions take the expressions:

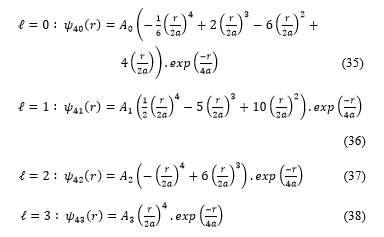 are constants which can be calculated with the normalization condition:

The calculations were made with  , the graphs are shown in figure (3) below:

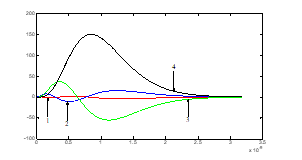Figure (3): The radial functions: , 1-red;  , 2-bleu; , 3-green; , 4-black (the x-axis in 10^-9 meter).

The probability density function gives the maximum probability of finding the electron at a position  on the radius of the sphere; this is reflected by a maximum of this function at the point . The graphs of probability density functions , for the hydrogen atom, are shown in figures (4, 5, 6 and 7):

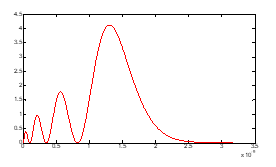Figure (4): density which has four maximums.

Figure (5): density  which has three maximums.

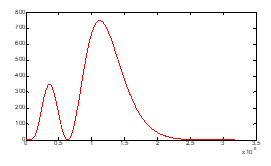Figure (6): density  which has two maximums.

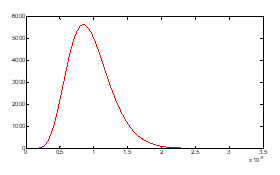Figure (7): density  which has one maximum.

5. The transcendental equation of the energy spectrum

Knowing the most general perfectly reflecting boundary condition by the equation (26), the energy spectrum is thus determined from the transcendental equation

This transcendental equation, which expresses the energy of the physical system, arises from the resolution of the Schrödinger equation and takes into account parameters relating to the quantification of the energy considered to be the real number k, and also of a second parameter ℓ, which is the azimuthally quantum number which generates the degeneration of the stationary states of energy. A third parameter, the self-adjoint extension parameter , is also considered  and concerns surface boundary conditions, taking into account the state of the surface as well as the material constituting the inner envelope of the cavity. In fact, this envelope must prevent the loss of energy at the atomic scale; the inside of the envelope is therefore made reflective so that all the particles arriving at the wall are deflected towards the inside of the cavity.

In the following, the expressions of the Bessel functions for  and (  +1) orders, and also the derivative:

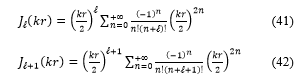
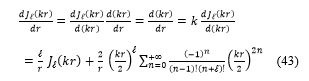Substituting these expressions, equations (41, 42 and 43) in the equation (40), the transcendental equation become:

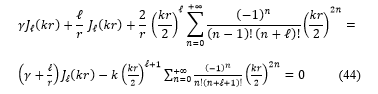5.1.  Calcul of the energies states

Consider now the equation giving the boundary condition for an indifferent position r:

The solution of this equation (45) was find as:

With applying the conditions at the wall of the cavity for r = R and at the center of the cavity for r = 0:

The exact wave function, which takes into account the self-adjoint extension parameter   , is then found like:

For , the boundary condition reduces to  , as well as the textbook case.

It is well know that, the wave function which is depending on the wave vector  and on the space vector  , is written as in the following form:

And for the radial component for r = R:

Therefore:

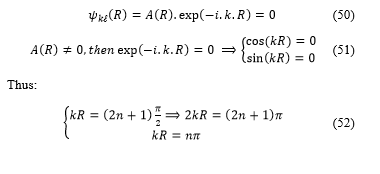
In order to know the meaning of the self-extension parameter, it is important to express the natural number  as a function of  according to the following relation:

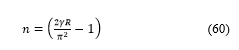and consequently, the energy as a function of  arises from equation (55) as:

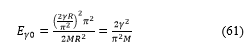It is then easy to obtain the two conditions:

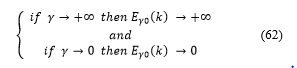These conditions, equation (61), mean that when the self-adjoint extension parameter   is high, tends to the infinite, the storage of the hydrogen energy is well good and there are little or no losses. On the other hand, when the self-adjoint extension parameter   is small, tends to zero, the hydrogen energy storage make many losses, and it is not good.

5.2.  Graphs of the energies states

The energy graph as a function of the radius R of the spherical cavity, , for the following values of  ( ) is shown in the figure (8).

For radii , the energies of the lowest level  are respectively (in Joules):

The graph of energy as a function of the self-adjoint parameter, , is shown in figure (9).

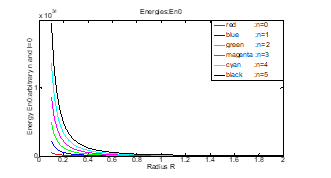Figure (8): Energy  with function of R and n

(n=0, 1, 2, 3, 4 and 5).

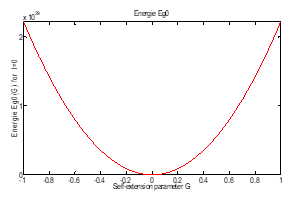Figure (9): Energy  with function of  .

The case, gamma tends towards infinity is treated previously and the energy depends on the number . There is no contradiction since energy tends to infinity in both cases: when  and  tend towards infinity.

6. Conclusion

This article studies both a free particle and an electron bound in a hydrogen atom confined to a spherical cavity with general perfectly reflecting boundary conditions characterized by

a self-adjoint extension parameter. It is well known that hydrogen gas need high pressure, about 700 to 800 bars, to minimize the volume because the hydrogen density is very small. And also the material of the cavity must be lightweight, like fullerenes or other aspects of nanotechnology, with a perfectly reflecting wall inside.

The subject requires much knowledge to take into account the thermodynamics effect like the pressure, so this modeling is based on the calculation of the wave functions especially the radial function. And also a calculation of the clean energies that are stored in the cavity was approached.

The solutions depend on the self-adjoint extension parameter which takes into account the physical properties of the cavity wall. For some values of this parameter, the radial wave function is expressed with function of the Laguerre polynomials. These radial functions tend quickly to zero (equal to zero at about   meter), this proves that the cavity must be made with a nanotechnology material.

The calculation of the clean energy inside the cavity indicates that the maximum storage is reached when the self-adjoint extension parameter tends to infinity this corresponds to R tending to zero. This is done experimentally by making the inside surface of the cavity perfectly reflective, and also impervious to the passage of electrons to the outside of the cavity. On the other hand, if this parameter tends towards (or equal) zero, particle leakage is important, which causes significant losses of energies (energy stored equal zero       for ).

1. -M. Joubert, F.Cuevas, M. Latroche et A. Percheron-Guégan, Stockage de l’hydrogène et risques, Journée du CUEPE 2005 « L’hydrogène, futur vecteur énergétique ? » Genève le 13 mai 2005.
2. Michels, J. de Boer, A. Bijl, Remarks concerning molecular interaction and their influence on the polarisability, Physica 4,  1937,
3. Sommerfeld, H. Welker, Advances in Quantum Chemistry: Theory of Confined Quantum Systems – Part One,  Ann. Phys. 424, 1938, 56.
4. R. de Groot, C.A. Ten Seldam, On the energy levels of a model of  the compressed hydrogen atom,  Physica 12, 1946, 669.
5. P. Wigner, Application of the Rayleigh-Schrödinger Perturbation Theory to the Hydrogen Atom,  Phys. Rev. 94, 1954, 77.
6. W. Fowler, Energy,  polarizability  and size of confined one-electron systems,  Mol. Phys. 53, 1984,  865.
7. O. Frömann, S. Yngve, N. Frömann,  The energy  levels  and  the corresponding normalized wave functions for a model of a compressed atom,      J. Math. Phys. 28, 1987, 1813.
8. V. Scherbinin, VI. Pupyshev, Electronic Structure of  Quantum Confined Atoms and Molecules,  Russ. J. Phys. Chem. 74, 2000, 292.
9. H. Al-Hashimi, U.-J. Wiese, Self-adjoint extensions for confined electrons: From a particle in a spherical cavity to the hydrogen atom in a sphere and on a cone, Annals of Physics 327, 2012, 2742-2759.
10. H. Mousa. Calcul efficace et direct des représentations de maillage 3D utilisant les harmoniques sphériques. Thèse de doctorat en informatique, Université Claude Bernard Lyon 1, septembre 2007.
11. Claude Cohen-Tannoudji, Bernard Diu & Franck Laloë ; Mécanique Quantique, (1973).
12. Albert Messiah ; Mécanique Quantique, 2 volumes, Dunod (1959). Réédité en 1995.
13. E. Byerly. Spherical Harmonics, chapter 6, pages 195–218. New York : Dover, 1959. An Elementary Treatise on Fourier’s Series, and Spherical, Cylindrical, and Ellipsoidal Harmonics, with Applications to Problems in Mathematical Physics.
14. W. Hobson. The Theory of Spherical and Ellipsoidal Harmonics. New York : Chelsea, 1955.
15. Landau and E. Lifchitz, Mécanique quantique. Edition MIR, Moscou (1966).
16. Landau and E. Lifchitz, Théorie quantique relativiste. Edition MIR, Moscou 1972.
17. Idris-Bey, Quantum study of hydrogen stored under high pressure in a spherical cavity, 8th International Conference on Modelling, Identification and Control (ICMIC-2016) Algiers, Algeria- November 15-17, 978-0-9567157-6-0 © IEEE 2016.
18. Ravindra Shinde and Meenakshi Tayade; Remarkable Hydrogen Storage on Beryllium Oxide Clusters: First Principles Calculations; Department of Physics, Indian Institute of Technology Bombay, Mumbai, Maharashtra 400076, INDIA., and Department of Chemistry, Institute of Chemical Technology, Mumbai, Maharashtra 400019, INDIA, 2016.
19. Lueking, A.; Yang, R. T. Hydrogen Spillover from a Metal Oxide Catalyst onto CarbonNanotubes—Implications for Hydrogen Storage. J. Catal. 2002, 206, 165–168.
20. Li, Y.; Yang, R. T. Hydrogen Storage in Metal–Organic Frameworks by Bridged Hydrogen Spillover. J. Am. Chem. Soc. 2006, 128, 8136–8137.
21. Zhou, J.; Wang, Q.; Sun, Q.; Jena, P. Enhanced Hydrogen Storage on Li Functionalized BC3 Nanotube. J. Phys. Chem. C 2011, 115, 6136–6140.
22. Dodziuk, H.; Dolgonos, G. Molecular modeling study of hydrogen storage in carbon nanotubes. Chem. Phys. Lett. 2002, 356, 79 – 83.
23. Li, C.; Li, J.; Wu, F.; Li, S.-S.; Xia, J.-B.; Wang, L.-W. High Capacity Hydrogen Storage in Ca Decorated Graphyne: A First-Principles Study. J. Phys. Chem. C 2011, 115, 23221– 23225.
24. Liu, C.; Chen, Y.; Wu, C.-Z.; Xu, S.-T.; Cheng, H.-M. Hydrogen storage in carbon nanotubes revisited. Carbon 2010, 48, 452 – 455.
25. Wu, H.-Y.; Fan, X.; Kuo, J.-L.; Deng, W.-Q. DFT Study of Hydrogen storage by Spillover on Graphene with Boron Substitution. J. Phys. Chem. C 2011, 115, 9241–9249.
26. R. Sabin, E. Brändas, S.A. Cruz (Eds.), Theory of Confined Quantum Systems, in: Advances in Quantum Chemistry, vol. 57, Academic Press, Elsevier, 2009.
27. ZEPP; Exercices de Mécanique Quantique, Vuibert (1975).
28. Eric W. Weisstein. Legendre Polynomial. From MathWorld : A Wolfram Web resource.
29. Hladik, M.Chrysos, P. E. Hladik, L. U. Ancarani, Mécanique quantique : Atomes et noyaux, applications technologiques, 3e Edition. DUNOD (2009).

(Click Here)

(Click Here)