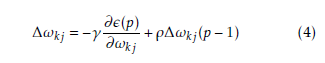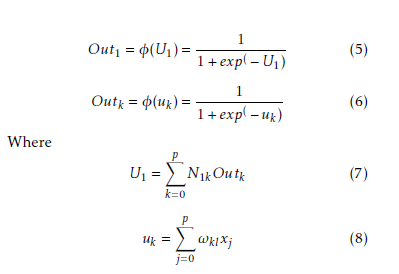1. Introduction

In the body, cancer is the uncontrolled enhancement of unusual cell. When the bodys normal control procedure stop the working, then cancer are build-up [1]. Old cells do not expire and in its place develop out of control, establishing fresh, abnormal cells. These additional cells may create a mass of tissue, called a tumor [2]. Leukemia is a cancer which starts in blood forming tissue, usually the bone marrow [3]. It leads to the over production of abnormal white blood cells [4]. However, the abnormal cells in leukemia do not function in the same way as normal white blood cells [5]. There are several types of leukemia, based upon how speedily the disease is growing up and the type of abnormal cells are generate. Peoples are may be affected at all stage by cancer [6]. In 2015, 54,270 people are prospective to be diagnosed with leukemia. The overall five-year correlative anointing rate for leukemia has more than four fold since 1960. From 1960 to 1965, the five-year correlative anointing rate among whites (only data available) with leukemia was 14%. From 1975 to 1980, the five-year correlative anointing rate for the total population with leukemia was 34.20% [7], and from 2004 to 2010, the overall correlative anointing rate was 60.30% [8]. From 20052010, the five-year relative correlative anointing overall were Chronic Myeloid Leukemia (CML) is 59.90% [9], Chronic Lymphocytic Leukemia (CLL) is 83.50%, Acute Myeloid Leukemia (AML) is 25.40% overall and

66.30% for children and adolescents younger than

15 years and Acute Lymphocytic Leukemia (ALL) is 70% overall [10], 91.80% for children and adolescents younger than 15 years, and 93% for children younger than 5 years. In 2015, 24,450 people are expected to die from leukemia with 14,040 males and 10,050 females [11]. In Us 2007-2011, leukemia was the fifth most common cause of cancer deaths in men and the sixth most common in women.

In the field of microarray data analysis, one of the most challenging remittance is gene selection [12]. In gene expression data normally contains a large number of variables genes compared to the numbers of samples [13]. The conventional data mining methodology cannot be directly used to the data due to this identity problem [14]. In this reason analysis of gene expression data used dimension reduction procedure [15]. The gene selection which deducts the genes extremely related to the pattern of every types disease in order to escape such problems [16]. Parametric and non-parametric tests are the statistical approach [17]. For example t-test and Wilcoxon rank sum test have been thoroughly used for searching differentially revealed genes since they are instinctive to understand and implement [18]. But they have a restriction to propagate, if more than two classes and require time swallowing coordination to solve the problem of multiple testing [19]. For three or more groups, the Kruskal-Wallis test can be used. But it may be created biased result because of reliance on the number of samples, when it is used to microarray data whose sample size are normally unbalanced [20]. Many diseases, they are reason by the problems such as chromosomal disequilibrium and gene mutations, which give away abnormal gene expression patterns. These pattern get the information about underlying genetic process and states of several types disease. If these patterns can be analyzed appropriately, they can be effective for recognize the disease sample and identifying the extent to which a patient is affliction from the disease and which can be help in the supervision of disease.

The microarray gene expression data have been collected to underlying biological process of a number of diseases [21]. It is very essential to narrow down from thousands of genes to a few disease genes and gene ranking [18]. In microarry data analysis genes selection is most important phase. For classification of data analysis, several forms of technique have been proposed for gene ranking [22]. These are classified into three several types: filter, wrapper and embedded process [23]. Each of these categories has its personal advantages and disadvantages. For example, filter process are computationally useful and simple but minor performance than the other process. On the other hand, wrapper and embedded procedure are comparatively much complicated and computationally costly but it usually gives excellent classification performance as they mainly apply classifier characteristics in gene ranking. Filter procedure include T-score, which is t-statistic standardized interrelation between input and output class labels [15]. On the other hand, wrapper and embedded procedure include Support Vector Machine (SVM) and its variants, random forest-RFE, elastic net, guided regularized random forest [24], balanced iterative random forest [25] etc . Main distinction of filter process and wrapper or embedded procedure is how they behave samples when ranking genes. For example, in filter procedure, all the samples are usually used for gene ranking but the quality and relevance data samples are ignore [26]. On the other hand wrapper or embedded procedure, classifier such as boosting algorithm, logistic regression, Support Vector Machine (SVM) etc., are used to gene ranking [27].

For complicated data analysis, we can used an Artificial Neural Network (ANN) model [28]. An ANN was externally used for solve the problem such as diagnosis of different types of cancer such as speech recognition, breast cancer [28] [29]and cervical cancer. Several types of effective researches on blood cells using neural network model has been committed [30]. Ongun et al enhancement a completely automated classification of bone marrow and blood using several types of way such as neural network and support vector machine (SVM). The best performance of SVM with accuracy of 91.05% as parallelism to Multilayer Perceptron (MLP) network using Conjugate Gradient Descent, Linear Vector Quantization (LVQ), and k-Nearest Neighbors (KNN) classifier which generate accuracy of 89.74%, 83.33% and 80.76% respectively.

In this paper, we proposed a method based on neural network models for identify a set of possible genes mediating the development of cancerous growth in cell. We said this model is Multilayer Perceptron Model-1 (MLP-1) and Multilayer Perceptron Model2 (MLP-2) [31]. At first we form group of genes using correlation coefficient, then we select the most important group. Finally, we present a set of possible genes get by this method, which may be responsible for cancerous growth in human cell. In this article, we consider three human leukemia gene expression data sets. The usefulness of the procedure, along with its excellent result over several others procedure, has been demonstrated three cancer related human leukemia gene expression data sets. The results have been compared seven existing gene selection methods like Support Vector Machine (SVM), Signal-toNoise Ratio (SNR), Significance Analysis of Microarray (SAM), Bayesian Regularization (BR), Neighborhood Analysis (NA), Gaussian Mixture Model (GMM), and Hidden Markov Model (HMM). The results are appropriately validated by some previous investigations and gene expression profiles, and compared using t-test, p-value, and number of enriched attributes. Moreover, the proposed procedure has get more number of true positive genes than the existing ones in identifying responsible genes.

2. Related Work

In this article, we have proposed procedure based neural network models for identification of cancer mediating genes. On existing gene selection methods, we have made a survey for comparative analysis [32]. Among them, we have select some existing gene selection methods like SVM, SNR, SAM, BR, NA, GMM, HMM.

SVM is a one type of machine learning procedure which is differ two classes by maximizing the margin between them [33]. For cancer classification, support vector machines (SVMs) is used to identify important genes [34]. The Lasso (L1) SVM and standard SVM are often considered using quadratic and linear programming procedure. A recurrent algorithm is used to solve the Smoothly Clipped Absolute Deviation (SCAD) SVM efficiently. Almost all the cases, it is noticed that with smaller standard errors the SCADSVM selects a smaller and a more stable number of genes than the L1-SVM. Another algorithm of gene selection using the weight magnitude as ranking criterion is Recursive Feature Elimination (RFE) SVM [35]. The SVM-RFE procedure ranks all the genes according to some scoring operation, and remove one or more genes with the lowest score values [36]. When the maximal classification accuracy is achieved, then the procedure will be stop [37].

Signal-to-noise ratio (SNR) is applied to rank the correlative genes according to their discriminative power. The procedure starts with the evaluation of a single gene, and frequently finding for other genes based on some statistical criteria [38]. The high SNR genes scores are select as the significant ones. Measurement of SNR score are affected by the size of variables [39]. When there are more than variables, the average and disunity of the other variables of another classes are dependent on the number of variables and data dispersion, which effect SNR ranking of the important variables due to the enhancement in noise in the data. The procedure is more efficient of finding and ranking a smaller number of important variables, when the number of variables can be decrease significantly. Significance analysis of microarray (SAM) is a one type of gene selection procedure which use a set of gene specific t-test and identify genes with statistical significant changing in expression values [40]. The basis of change in the gene expression values, every gene is assigned a score value. If the gene score value the greater than a threshold value which indicate potentially significant [41]. False Discovery Rate (FDR) is the percentage of such genes identified by chance [42]. In order to calculate FDR, insignificance genes are identified by analyzing layout of the measurements. Identify the smaller or larger sets of genes can be adjusted by using threshold value, and FDRs are computed for every set. The main problem is that, in permutation step where entire gene group are put in one group for evaluation. This needs an expensive computation and it likely confuses the analysis because of the noise in gene expression data. A simple Bayesian procedure has been used to remove the regularization parameter [43]. The value of a regularization parameter is determined by degree of sparsely, which is get an optimal result. Normally this include a model selection step, and calculate the minimization of cross validation error based on intensive search.

Neighborhood analysis (NA) is a procedure for clustering multivariate data analysis based on a given distance metric over the data. Functionally, purpose of NA and K-nearest neighbor algorithm are same [44]. Any significant correlation cannot detect and this is the main disadvantage. This problem may be due to the few number of genes and also likely that the phenotype is too complicated to be connected with a cluster of genes, and a more extend relationship may present in gene expression.

A Gaussian mixture model (GMM) is represented as a weighted sum of gaussian component densities which is based on a parametric probability density function [45]. For parameter selection GMM has been used. We have designed GMM on microarray gene expression data for gene selection. On the other hand, for genes identification, we have designed Hidden Markov Model (HMM) on microarray gene expression data sets. Normally HMMs provide an intuitional framework for representing genes with their several functional properties, and proficient algorithms can be creating to use these models to identify genes.

3. Methodology

Let us assume a set G = (g₁,g₂,….,g_i) of i genes are known which is hold the normal samples for first m expression values and diseased samples for subsequent n expression values. Now correlation coefficient of gene based normal samples are calculated. Therefore, correlation coefficient R_qr within q^th and r^th is given by [46] [47]

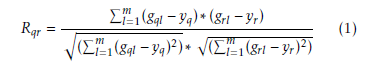Here y_q and y_r are the mean of expression values of q^th and r^th, gene respectively in normal samples. Similarly, for diseased samples the iteration coefficient R_qr between q^th and r^th genes is given by

Using equation 1 and 2 each pair of genes is computed. The genes are located in the similar group if R_qr ≥ 0.5. Now we have used interrelation coefficient to narrow down hearted the invention space by searching genes of a comparable behavior in terms of related expression patterns. The set of responsible genes mediating certain cancers are recognized in this procedure. The choice of 0.50 as a threshold value has been done through extensive experimentation for which the distances among the cluster center have become maximize [48]. The main set of genes is obtained in this pathway [49].

An extremely simplified model of biological structures is an Artificial Neural Networks that imitative the conduct of the human brain. A huge number of interrelated processing components of the layered structure is composed and intended to imitative biological neurons. MLP model is the one of the most popular ANN types with back-propagation algorithm. Figure 1, show the architecture of MLP model containing of interconnected neurons of three layers [50]. This three layers are input layer, hidden layer, and output layer [51]. This model is represented as n×p×q. Where input layer consist of n number of neurons, hidden layer consist of p number of neurons and output layer consist of q number of neurons. In the higher layer every neuron in every layer is completely attached to all neurons and every link has a weight connected with it. In interconnected neurons, these weights are define the nature and strength of the influence. The output signals from one layer are conducted to the consequent layer by using links that amplify the signals based on the interconnected weights [52]. Exception of the input layer neurons, the total input of every neuron is the sum of weighted outputs of the previous layer neurons. In hidden and output layers neurons, we can calculate the output by using

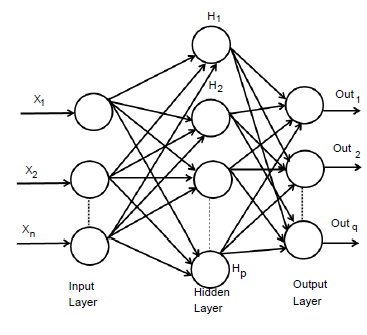Figure 1: Architecture of an MLP network

Hidden layer neurons execute a non-linear alteration that qualifies the MLP model to simulate a more difficult and non-linear structure within the constraints of a three layer MLP model and more than one hidden layer are used. By employing an incremental adaptation approach, the MLP model has generalized curve fitting capability. Input patterns and output patterns was carried out by MLP model and specified proportion is randomly selected. A learning procedure to correct the linking weights recurrently and to reduce the system error mechanism by every forward processing of the input signal by using back-propagation algorithm. In the initial stage of the learning procedure, to create a input pattern from the input layer to the output layer. The error of every output neuron was calculated from the difference between the calculated and desired outputs. ε(p) is the system error of p^th training pattern, which is defined as

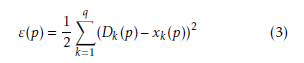Where D_k(p) and x_k(p) are the k^th element of the desired output and calculated output respectively. On the other hand number of neurons in output layer is q. Readjustment of the weights in the hidden layers and output layers is the next step by using a generalized delta rule which is minimizing the distinction between the desired outputs and calculated outputs.

Every interconnection weight of the incremental correction can be calculated by

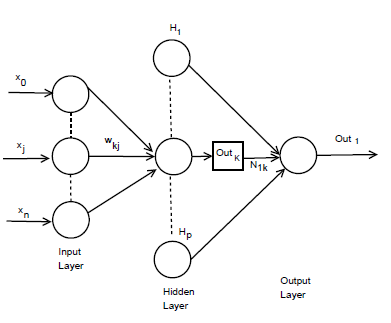Figure 2: n×p×1 MLP model architecture.

The incremental correction of the interconnection weight between j^th neurons and k^th neuron is ∆ω_kj(p), in the last iteration, the incremental correction is ∆ω_kj(p − 1) learning rate is γ and the range of 0 < γ < 1, momentum factor is the ρ and range is 0 ≤ ρ < 1. By using learning rate the updated weight is control and improve of the effectiveness of learning procedure by using momentum. Training set carried when the squared errors of average sum are over and all training patterns was globally reduced. On training period completion, the testing period was conduct those input pattern which was not present in the training set. Now we consider a MLP model with n×p×1 network. Input layer, hidden layer and output layer are n, p, 1 respectively. Show in Figure 2. For both hidden and output neurons was select sigmoid function as the activation function. The mapping function of input-output are realize by the network Out₁ can be computed as

Algorithm 1 Training procedure – MLP-1 Step 1: Initialize all weight and bias. Step 2: While terminating condition is not satisfied; Step 2.1 For each training tuple; propagate the input forward, Step 3: For each output layer of unit q, Step 3.1: Output of an input unit, which is actual input values, Step 4: For every hidden layers or output layers, Step 4.1: Compute the net input of unit q with respect to the previous layer p; Step 4.2: Compute the output of q, layer. Step 5: Compute the error of output layer of unit q; Step 6: Compute the error with respect to the next higher layers. Step 7: Increment the weight of every layers. Step 8: Update the weight of every layers. Step 9:Increment the bias of every layers. Step 10: Update the bias of each layers. Step 11: After some iteration, when all ∆ωpq in the previous epoch were so small as to bellow specified threshold 0.05, then the procedure will be stop. Algorithm 2 Training procedure – MLP-2 Step 1: Initialize the weight and bias. Step 2: Perform a vector of row which is the weight interconnection between the hidden layers (p nodes) and output layer. Step 2: Perform n×p× matrix and interconnection weights between the input nodes (n) and hidden nodes (p) is ω. Step 3: Row vector are computed. Step 4: Relative weight of input node are computed. Step 4: After some iteration, when all weight values in the previous epoch were so small as to bellow specified threshold 0.05, then the procedure will be stop.

Interconnection weight between the k^th hidden neuron and output neuron is N_1k interconnection weight between the k^th hidden neuron and j^th input neuron is ω_kj. In the j^th hidden neuron the output value is

Out_k. x_j is the input of the j^th input neuron, where Out₀ = −1. The case belongs to class 1, where Out ≥ 0.05 and case belongs to class 0 where Out₁ < 0.05. A node can recognized an output of that node given an input or set of inputs by using activation function. A linear access can be produce 1 or 0 output, but non-linear process the activation function can be generate the output in the specific limit. The activation function can be accepted large forms construct on the data sets. A set of training samples, comparing the networks prediction for each sample with the actual known class level are frequently generating by using back-propagation learning method. The weights are changes as to minimize the mean squared error between the actual class and the prediction network for each sample. The weight and every bias are initialized to small random number of the network. Now we can calculate the total input and output of each unit in the output layer and hidden layer. At first the sample are fed to the input layer of the network. Note that for unit q in the input layer, its output is equal to its input, that is Out_q = η_q for input q. Given an unit q in a hidden layer or output layer, the net input η_q, to unit q is

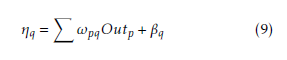Where ω_pq is the weight of the connection from unit p in the previous layer to unit q; Out_p is the output of unit p from the previous layer and β_q is the bias of the unit. Given the net input η_q to unit q and output of unit q is computed as

The error is created backwards by updating the weight and bias in the network. For a unit q in the output layer, the error κ_q is computed by

Where Out_q is the actual output of unit q and χ_q is the true output. The error of hidden layer of unit of unit q is

Where α_qr is the weight of the connection from unit q to unit r and κ_r is the error of unit r. Now the weight of every layer are incremented and update the weight value of each layer.

∆ωpq = (µ)κqOutq	(13)
ωpq = ωpq +∆ωpq	(14)

Now the bias of every layer are incremented and update the all bias value of each layer.

∆βq = (µ)κq	(15)
βq = βq +∆βq	(16)

After some iteration, when all ∆ω_pq in the previous epoch were so small as to bellow specified threshold 0.05, then the procedure will be stop. The procedure will be describe in algorithm 1 and algorithm 2.

4. Description of the Data sets

In this work, we can select three types of leukemia gene expression data sets. The data sets ID is GDS-2643, GDS-2501, GDS-3057 and title of the data set is Waldenstrom’s macroglobulinemia (B lymphocytes and plasma cells), B-cell chronic lymphocytic leukemia, and Acute Myeloid Leukemia respectively. The data base web link is http://ncbi.nlm.nih.gov/projects/geo/.

The data set (GDS-2643) consists of 22,283 numbers of genes with 56 samples. Among them, there are 13 normal samples which consist of 8 normal for B lymphocytes and 5 normal plasma cells and 43 diseased samples which consist of 20 Waldenstrom’s macroglobulinemia, 11chronic lymphocytic leukemia, 12 multiple myeloma samples.

The dataset (GDS-2501) data set consists of 22,283 numbers of genes with 16 samples. In this sample analysis of B-cell chronic lymphocytic leukemia (B-CLL) cells that express or do not express zetaassociated protein (ZAP-70) and CD38. The prognosis of patients with ZAP-70-CD38- B-CLL cells is good, those with ZAP-70+CD38+B-CLL cells is poor.

The dataset (GDS-3057) content 26 Acute Myeloid Leukemia (AML) patients with normal hematopoietic cells at a variety of different stages of maturation from 38 healthy donors The total data set consist of 22,283 number of genes with 64 samples. Among them, there are 38 normal samples which contents 10 normal for bone marrow, 10 normal samples for peripheral blood, 8 normal samples for bone marrow CD34 plus and 10 normal samples for Primed peripheral blood hematopoietic stem cells (PBSC) CD34 plus. On the other hand there are 26 leukemia samples which contents 7 bone marrow and 19 peripheral bloods.

5. Comparative Performance Evaluation of the Models

In this section, the usefulness of the procedure has been demonstrated three types of human leukemia gene expression data sets. Now we can apply comparative analysis with seven existing methods like SVM, SNR, SAM, BR, NA, GMM and HMM. We have applied this procedure on the gene expression data sets for selecting important genes. We have found two classifier groups. One is normal class and another is disease class. After some iteration, we have found normalized value of every gene. Here we have considered a threshold value which is 0.05. After normalization if the gene value is grater then 0.05, then which types of gene is normal gene. After normalization if the gene value is less than 0.05, then which types of gene is disease gene. We consider several genes that are most significant of our experiment. The gene expression values are significantly changes from normal samples to diseased samples. Applying this process on the first data set (GDS-2643), we have found that genes like CYBB, TPT1 and PRDM2 among the most important genes which are over the expressed the diseased samples. On the other hand CRYAB minimize the expression value and fully significant in diseased samples. The gene are recognize as an under expressed gene. In order to limited size of manuscript, we have showed only the profile plots of genes of GDS-2643 data set (depicted in Figure 3 ). In the case of GDS-2501 data set, the genes like ACTB, CENPN, ALCAM, PXN have changed their expression values for normal samples to diseased samples. Similarly, the dataset GDS-3057, like TDG, CTIF, LLS, NAB2 have changed their expression values for normal samples to diseased samples. The usefulness of the methodology has been shown three types of leukemia gene expression data. We have applied the methodology on the aforesaid gene expression data sets for selecting some important gene intercede diseases. Now we have applied the procedure on the previous gene expression data sets for selecting some important diseases mediating genes. In this procedure, at first based on correlation values the genes are placed into group. For GDS-2643, we have found six groups which holding 1869, 1131, 1033, 601, 537 and 1208 number of genes (Table 5). The most important group by both MLP-1 and MLP-2 has been selected 1869 number of group genes. Now we have considered two classes for both MLP-1 and MLP-2. One is normal samples class and other is diseased samples class. ω is a weight coefficient value which is initialized by random numbers. Both MLP1 and MLP-2, we have found 28 and 30 number of genes respectively, when grouping of genes and most important groups selection are completed. Now we have found 20 numbers genes that are present in both procedure. Among them, based on their ω values we have selected 18 number of genes.

Similarly in GDS-2501, we have found eight groups which containing 652, 1031, 1217, 1301, 816, 539, 741 and 912 number of genes. Similarly in GDS-3057, eight group of genes which contain 2521, 2624, 2241, 2341, 2471, 803, 2191, and 2238. Now we have found 1869 genes for GDS-2643, 1217 genes for GDS-2501 and 2624 genes for GDS-3057 respectively by applying both MLP-1 and MLP-2. Finally we have found 24, 21 and 20 number of most important genes corresponding to the three data set by using MLP-1. On the other hand we have found 25, 21 and 19 number of most important genes corresponding to the three data set by using MLP-2. The number of genes which is found by both MLP-1 and MLP-2 are 18, 21 and 17 to these data sets. Table (5) show that for different sets of genes the number of functionally enriched attributes corresponding to these methods. It has been found that both procedure MLP-1 and MLP-2 performed the best results for all data sets. These results show that

Data set ID Selected group No of selected groups from selected group Group No genes in each group GDS-2643 1 18 1 1869       2 1131       3 1033       4 601       5 537       6 1208 GDS-2501 2 21 1 652       2 1031       3 1217       4 1301       5 816       6 539       7 741       8 912 GDS-3057 4 17 1 2521       2 2624       3 2241       4 2341       5 2471       6 803       7 2191       8 2238 Table 1: Selection of groups and genes for different data set

the both MLP-1 and MLP-2 procedure has been able to select the more number of important genes responsible for mediating a disease than the other seven existing procedure.

5.1. Validation of the Result

In this part, we have analysis the results which is founded by different types of procedure including MLP-1 and MLP-2. In this comparison we have using p-value, t-test, biochemical pathways, F-test and sensitivity.

5.1.1. Statistical Validation

Prosperity of every GO attributes of every genes has been computed by its p-value. When the p-value is low, it means that the genes are biologically significant. Now we have create a comparative analysis, by using some other procedure like SVM, SNR, SAM, BR, NA, GMM and HMM. For different sets of genes Table 2 show that number of functionally enriched attributes corresponding to these procedure. For all data set we have been show that MLP-1 and MLP-2 performed the best result. The more important genes are select by these procedure are show in these results. Both NFM-1 and NFM-2 are accomplished of getting more number of true positive genes in terms of identifying the GO attributes and cancer attributes with respect to other existing procedure are depicted in Figure(4). Now we have 478 GO attributes of 375 gene set are identified among them 102 GO attributes of cancer related are identified.

Now we validate the results statistically, we have performed t-test on the genes identified by DLM on each data sets. t-test is the statistical significance which indicate whether or not the difference between two groups average most likely reflects an original difference in the population from which the group wear sampled. The t-value show the most significant genes (99.9%) which p-value <0.001. For this three types of data set we can apply t-test and we get corresponding t-value. We have identify some important genes like IARS (4.78), MMP25 (5.68), TYMS (4.96), HPS6 (5.24), MLX (4.12), CALCA (4.32), HIC2

(4.12), ANP32B (5.16), TFPI (4.51), CRYAB (3.08), NCF1C (3.71), HNRNPH1 (3.12), etc. The number in the bracket shows t-value of the corresponding gene. The t-value of this genes exceeds the value for p = 0.001. This means that this gene is highly significant (99.9% level of significance). Similarly genes like ERCC5 (3.52), PRDM2 (3.45), PRIM2 (2.54), TPT1 (3.35), RPS26 (2.41), EFCAB11 (3.71), PRPSAP2 (3.43), PRKACA (2.44), etc exceed the tvalue for P = 0.01. It indicated that this gene is significant at the level of 99%. Similarly genes like MED17 (2.55), MAPK1 (2.35), PIK3CB (2.45), NMD3

(2.15), ARG2 (2.16), EXOC3 (2.56), WHSC1 (2.71), RFC4 (2.35), GLB1L (2.71), HNF1A (2.41) etc exceeds the value for P = 0.05. It indicate that this genes significant at the level of 95%. Similarly genes like FLG (1.77), TXNL1 (1.24), RIN3 (1.34), CYBB (2.31),

ZNF814 (1.45), KLF4 (1.18) etc exceeds the value for P = 0.1. It indicate that this type of genes significant at the level of 90%.

In GDS-2643, we have found cancer pathway for non-small cell and small cell leukemia. In these two

Data set	Gene Set	MLP-1	MLP-2	SVM	SNR	SAM	BR	NA	GMM	HMM
GDS-2643	First 5	60	58	59	10	12	15	10	27	20
	First 10	72	73	65	17	18	20	13	32	25
	First 15	77	79	71	21	22	26	12	41	29
	First 20	79	92	76	30	26	30	16	45	34
GDS-2501	First 5	83	78	85	15	55	48	33	39	48
	First 10	88	85	88	24	62	55	41	44	60
	First 15	101	98	95	31	68	72	52	51	55
	First 20	107	106	103	39	84	65	66	68	77
GDS-3057	First 5	45	52	37	21	24	26	24	19	20
	First 10	63	62	46	35	30	29	33	25	28
	First 15	67	65	57	37	29	31	39	27	35
	First 20	69	70	55	41	31	35	42	36	39

Table 2: Result of several sets of genes on number of attributes

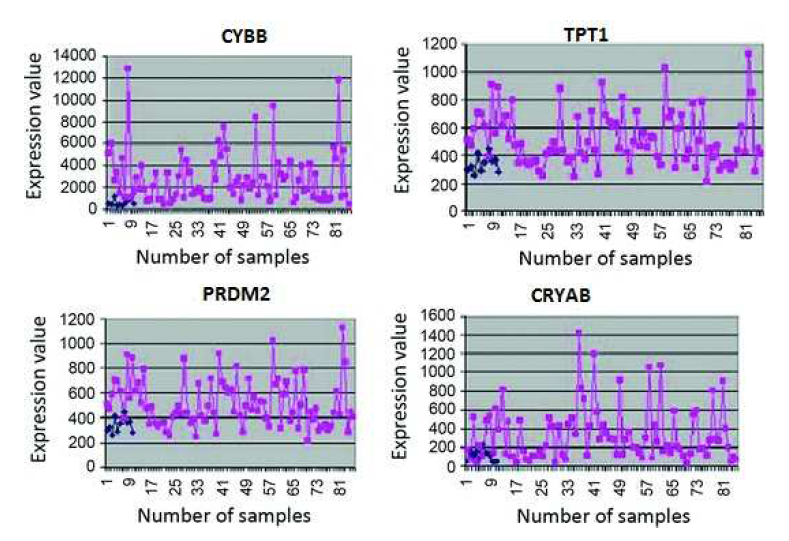Figure 3: Expression profiles of some over-expressed genes (CYBB, TPT1, PRDM2) and under-express (CRYAB) in normal (shown by blue points) and disease (shown by red points) sample of human leukemia expression data.

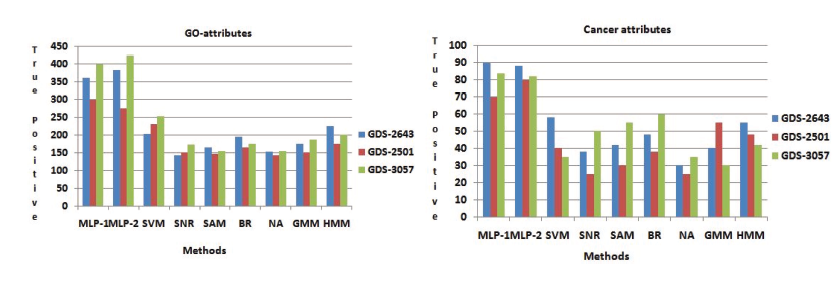Figure 4: Identification of GO attributes and Cancer attributes the Performance comparisons of MLP-1 and MLP-2 with other seven existing methods.

Comparison among the methods in biochemical pathway

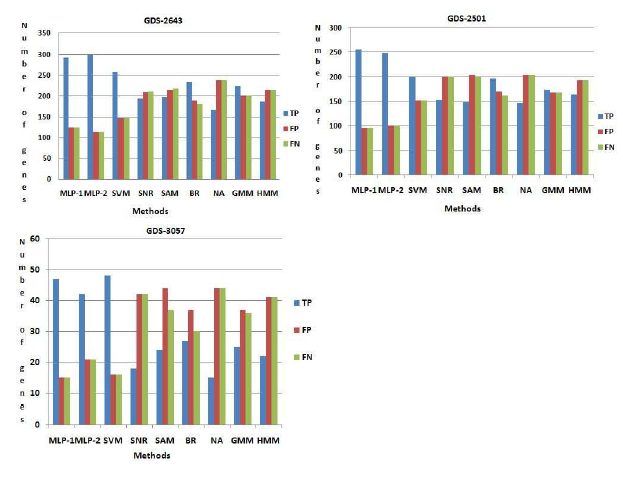Figure 5: Comparison among the methods. Here T P , FP , FN indicate the number of truepositive, f alsepositive, f alsenegative respectively.

pathway we have found 407 number of genes. Now this set of genes, are compared with those obtained by seven existing procedures. Here 293 and 300 number of genes are identified which is common in database information and the results of both MLP-1 and MLP-2, respectively. These genes are called truepositive(T P ) genes. In top rank 407 genes, we have found 116 and 110 number of genes are present respectively in both procedure MLP-1 and MLP-2 but not present these pathway. These genes are called f alsepositive(FP ) genes. Similarly we have found 116 and 110 number of genes are f alsenegative(FN) for both MLP-1 and MLP-2 procedure respectively. Now we have calculate the number of truepositive(T P ), f alsepositive(FP ) and f alsenegative(FN) genes for other seven existing methods. From Figure (5) show that both NFM1 and NFM-2 procedure have been able to identify more number of truepositive genes, but less number of f alsepositive and f alsenegative genes compared to all the other procedures. Similarly in GDS2501 and GDS-3057, we have been able to identify more number of truepositive genes, but less number of f alsepositive and f alsenegative genes compared to all the other procedures and result are show in Figure

(5).

5.1.2 .Biological Validation

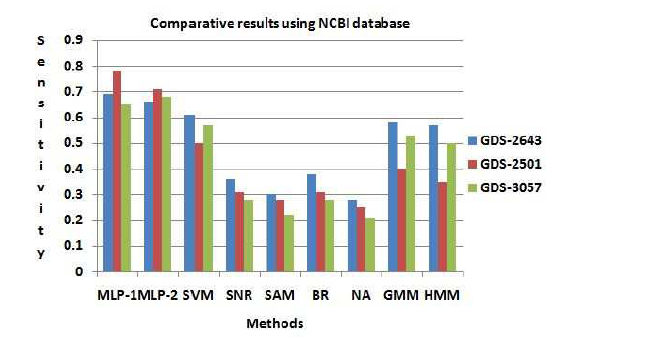
The disease mediating gene list corresponding to a specific disease can be founded by a gene database At first we have computed the total number of true positive genes for every data set for every procedure. As our result, Sensitivity of both MLP-1 and MLP-2 procedure is more than the other existing procedure. Figure (7) show that Sensitivity of both MLP-1 and

MLP-2 has performed the best for GDS-2501 data set.

6. Conclusion

In this article, we have proposed a model based on multilayer perceptron, which will select the genes that have been changed quite significantly from normal stage to disease stage. Base on vale of correlation, the different types of genes can be obtained and we have found most important groups. The gene of these groups are evaluated by using both procedure MLP1 and MLP-2. The most important genes are gained by the procedure have also been corroborated by pvalues of genes. The best result of the procedure compression too few standing once has been demonstrated. The output have been corroborated using biochemical pathway, p-value, t-test, sensitivity and some existing result expression profile plots. It has been obtained that the procedure has been capable to the genes are most significant.

Appendix

We have found several set of genes for GDS-2643,

GDS-2501 and GDS-3057 respectively. For GDS2643, by using both MLP-1 and MLP-2, we have identified 351 numbers of genes. Now we have compared this set of genes with 351 genes from NCBI and both MLP-1 and MLP-2 can be identified 247 and 241 number of genes respectively, which is common both sets. These genes said truepositive(T P ). On the other hand, (351-247) = 104 and (351-241) = 110 number of genes are not present the list of genes which is found from NCBI for both procedure MLP1 and MLP-2 respectively. These numbers of gene are called f alsepositive(FP ) genes. Similarly (351247) = 104 and (351-241) = 110 number of genes are present NCBI database but not present in the set of genes which is found by both procedure MLP-1 and MLP-2 respectively. These numbers of gene are called f alsenegative(FN) genes. Likewise other procedure, viz., SVM, SNR, SAM, BR, NA, GMM, HMM are compared our result on GDS-2643, GDS-2501 and GDS3057 respectively. Figure (6) show that both MLP-1 and MLP-2 found the more number of true positive (TP) genes then the other existing procedure for GDS2643, GDS-2501 and GDS-3057 respectively.

Now we can order to validate our result and calculate the Sensitivity of gene expression data sets. The Sensitivity is computed by using following formula:

T P

Sensitivity =      (17) T P +FN

F-score: F-score are a statistical method for determining accuracy accounting for both precision and recall. The formula for traditional F-score is, F-score= 2∗(precision ∗ recall/precision + recall). Where precision = T P /T P +FP , Recall = T P /T P +FN.

True Positive: A true positive test result is one that detect the condition when the condition is present. True positive rate = T P /(T P +FN).

False Positive: A false positive is an error in some rating method in which a condition tested for is badly found to have been detected. A false positive test result is one that detect the condition when the condition is absent. False positive value = FP /(FP +T N). False Negative: A result that appears negative when it should not. A false negative test result is one that does not detect the condition when the condition is present. False negative value = FN/(T P +FN). True Negative: A true negative test result is one that does not detect the condition when the condition is absent. True negative value = T N/(T N +FP ).

Conflict of Interest The authors declare no conflict of interest.

Acknowledgment

This work has been supported by the University Grant Commission (UGC) RGNF2014-15-SC-WES-69906, Govt of India and TEQIP-II Project, University of Calcutta.

Comparison among the methods using NCBI database

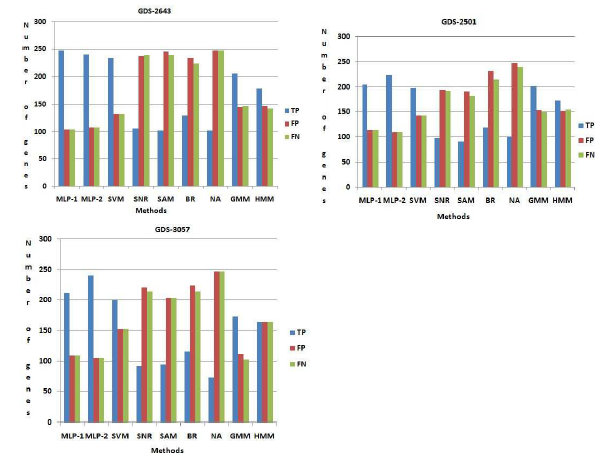Figure 6: Comparison among the methods using NCBI database. Here T P , FP , FN indicate the number of truepositive, f alsepositive, f alsenegative respectively.

Figure 7: Comparison among the methods using NCBI database.

1. K. Veettil, K. G. Lim, N. Chaiyakunapruk, S. M. Ching, M.R. Abu Hassan, “Colorectal cancer in Malaysia: Its burden and implications for a multiethnic country, Asian Journal of Surgery, 2016. 10.1016/j.asjsur.2016.07.005
2. Seewald, J. W. Taub, K. W. Maloney, E. R.B. McCabe, “Acute leukemias in children with Down syndrome, 107(1), 25-30, 2012. 10.1016/j.ymgme.2012.07.011
3. F. Zeidner, J. E. Karp, “Clinical activity of alvocidib (flavopiridol) in acute myeloid leukemia, Leukemia Research, 39(12), 1312-1318, 2015. 10.1016/j.leukres.2015.10.010
4. L. Sielken Jr, C. V.-Flores, “A comprehensive review of occupational and general population cancer risk: 1,3- Butadiene exposureresponse modeling for all leukemia, acutemyelogenous leukemia, chronic lymphocytic leukemia, chronic myelogenous leukemia, myeloid neoplasm and lymphoid neoplasm, Chemico-Biological Interactions, 241, 50- 58, 2015. 10.1016/j.cbi.2015.06.009
5. Ripperger, B. Schlegelberger, “Acute lymphoblastic leukemia and lymphoma in the context of constitutional mismatch repair deficiency syndrome, European Journal of Medical Genetics, 59(3), 133-142, 2016. 10.1016/j.ejmg.2015.12.014
6. Mezei, M. Sudan, S. Izraeli, L. Kheifets, “Epidemiology of childhood leukemia in the presence and absence of Down syndrome, Cancer Epidemiology, 38(5), 479-489, 2014. 10.1016/j.canep.2014.07.006
7. Izraeli, “The acute lymphoblastic leukemia of Down Syndrome Genetics and pathogenesis, European Journal of Medical Genetics, 59(3), 158-161, 2016. 10.1016/j.ejmg.2015.11.010
8. Suzuki, A. Shigeta, T. Fukunaga, “Death resulting from a mesenteric hemorrhage due to acute myeloid leukemia: An autopsy case, Legal Medicine, 16(6), 373-375, 2014. 10.1016/j.legalmed.2014.07.003
9. F. Zeidner, J. E. Karp, “Clinical activity of alvocidib (flavopiridol) in acute myeloid leukemia, Leukemia Research, 39(12), 1312-1318, 2015. 10.1016/j.leukres.2015.10.010
10. P. H. Lin, C. C. Lin, H. I. Yang, L. Y. Li, L. Y. Bai, C. F. Chiu, Y. M. Liao, C. Y. Lin, C.Y. Hsieh, C. Y. Lin, C. M. Ho, S. F. Yang, C. T. Peng, F. J. Tsai, S. P. Yeh, “Prognostic impact of allogeneic hematopoietic stem cell transplantation for acute myeloid leukemia patients with internal tandem duplication of FLT3, Leukemia Research, 37(3), 287-292, 2013. 10.1016/j.leukres.2012.10.005
11. Seewald, J. W. Taub, K. W. Maloney, E. R.B. Mc- Cabe, “Acute leukemias in children with Down syndrome, Molecular Genetics and Metabolism, 107(1), 25-30, 2012. 10.1016/j.ymgme.2012.07.011
12. Ghosh, R. K. De, “Fuzzy Correlated Association Mining: Selecting altered associations among the genes, and some possible marker genes mediating certain cancers, Applied Soft Computing, 38, 587-605, 2016. 10.1016/j.asoc.2015.09.057
13. Ghosh, R. K. De, “Development of a fuzzy entropy based method for detecting altered gene-gene interactions in carcinogenic state, Journal of Intelligent & Fuzzy Systems, 26, 2731-2746, 2014. 10.3233/IFS-130942
14. Ghosh, R. K. De, “Linguistic Recognition System for Identification of Some Possible Genes Mediating the Development of Lung Adenocarcinoma, Inf. Fusion, 10, 260-269, 2009. 10.1016/j.inffus.2008.11.007
15. A. Mundra, J. C. Rajapakse, “Gene and sample selection using T-score with sample selection, Journal of Biomedical Informatics, 59, 31-41, 2016. 10.1016/j.jbi.2015.11.003
16. Ghosh, R. K. De, “Identification of certain cancermediating genes using Gaussian fuzzy cluster validity index, Journal of Biosciences, 40(4), 741-754, 2015. 10.1007/s12038-015-9557-x
17. Tabakhi, A. Najafi, R. Ranjbar, P. Moradi, “Gene selection for microarray data classification using a novel ant colony optimization, Neurocomputing, 168, 1024-1036, 2015. 10.1016/j.neucom.2015.05.022
18. Saha, D. B. Seal, A. Ghosh, K. N. Dey, “A Novel Gene Ranking Method Using Wilcoxon Rank Sum Test and Genetic Algorithm, Int. J. Bioinformatics Res. App, 12, 263-279, 2016. 10.1504/IJBRA.2016.078236
19. Ongun, U. Halici, K. Leblebicioglu, V. Atalay, M. Beksac, S. Beksac, “Feature extraction and classification of blood cells for an automated differential blood count system, ”Neural Networks, 2001. Proceedings. IJCNN ’01. International Joint Conference on, 4, 2461-2466, 2001. 10.1109/IJCNN.2001.938753
20. H. Zhang, J. Ahn, X. Lin, C. Park, “Gene Selection Using Support Vector Machines with Non-convex Penalty, Bioinformatics, 22, 88-95, 2006. 10.1093/bioinformatics/bti736
21. Ghosh, R. K. De, “Interval based fuzzy systems for identification of important genes from microarray gene expression data: Application to carcinogenic development, Journal of Biomedical Informatics, 42, 1022-1028, 2009. 10.1016/j.jbi.2009.06.003
22. Ghosh, B. C. Dhara, R. K. De, “Comparative Analysis of Cluster Validity Indices in Identifying Some Possible Genes Mediating Certain Cancers, Molecular Informatics, 32(4), 347-354, 2013. 10.1002/minf.201200142
23. Elyasigomari, M.S. Mirjafari, H.R.C. Screen, M.H. Shaheed, “Cancer classification using a novel gene selection approach by means of shuffling based on data clustering with optimization, Applied Soft Computing, 35, 43-51, 2015. 10.1016/j.asoc.2015.06.015
24. D. Uriarte, S. A. de Andres, “Gene selection and classification of microarray data using random forest, BMC Bioinformatics, 7(1), 1-13, 2006. 10.1186/1471-2105-7-3
25. Deng, G. Runger, “Gene selection with guided regularized random forest, Pattern Recognition, 46(12), 3483-3489, 2013. 10.1016/j.patcog.2013.05.018
26. Anaissi, P. J. Kennedy, M. Goyal, D. R. Catchpoole, “A balanced iterative random forest for gene selection from microarray data ,BMC Bioinformatics , 14(1), 1-10, 2013.10.1186/1471-2105-14-261
27. Guyon, J. Weston, S. Barnhill, V. Vapnik, “Gene Selection for Cancer Classification using Support Vector Machines, Machine Learning, 46(1), 389-422, 2002. 10.1023/A:1012487302797
28. A. Menndez, F. J. de Cos Juez, F. S. Lasheras, J. A. A Riesgo, “Artificial neural networks applied to cancer detection in a breast screening programme, Mathematical and Computer Modelling, 52, 983-991, 2010. 10.1016/j.mcm.2010.03.019
29. C.Sharma, G. P.Tuszynski, M. R.Blackman, M. Sharma, “Long-term efficacy and downstream mechanism of antiannexinA2 monoclonal antibody (anti-ANX A2 mAb) in a pre-clinical model of aggressive human breast cancer, Cancer Letters, 373(1), 27-35, 2016. 10.1016/j.canlet.2016.01.013
30. V. da Silva, R. V. A. Monteiro, F. A. M. Moura, M. R. M. C. Albertini, M. A. Tamashiro, G. C. Guimaraes, “Performance Analysis of Neural Network Training Algorithms and Support Vector Machine for Power Generation Forecast of Photovoltaic Panel, IEEE Latin America Transactions, 15(6), 1091- 1100, 2017. 10.1109/TLA.2017.7932697
31. Daz-Rodrguez, J. C. Cancilla, G. Matute, D. Chicharro, J. S. Torrecilla, “Inputting molecular weights into a multilayer perceptron to estimate refractive indices of dialkylimidazolium-based ionic liquidsA purity evaluation, Applied Soft Computing, 28, 394-399, 2015. 10.1016/j.asoc.2014.12.004
32. Dashtban, M, Balafar, “Gene selection for microarray cancer classification using a new evolutionary method employing artificial intelligence concepts, Genomics, 109(2), 91-107, 2017. 10.1016/j.ygeno.2017.01.004
33. Guyon, J. Weston, S. Barnhill, V. Vapnik, N. Cristianini, “Gene selection for cancer classification using support vector machines, Machine Learning, 389-422, 2002.
34. D. A. Vanitha, D. Devaraj, M. Venkatesulu, “Gene Expression Data Classification Using Support Vector Machine and Mutual Information-based Gene Selection, Procedia Computer Science, 47, 13-21, 2015. 10.1016/j.procs.2015.03.178
35. Mishra, D. Mishra, “SVM-BT-RFE: An improved gene selection framework using Bayesian T-test embedded in support vector machine (recursive feature elimination) algorithm, Karbala International Journal of Modern Science, 1(2), 86-96, 2015. 10.1016/j.kijoms.2015.10.002
36. Tang, Y. Q. Zhang, Z. Huang, “Development of Two- Stage SVM-RFE Gene Selection Strategy for Microarray Expression Data Analysis, IEEE/ACM Transactions on Computational Biology and Bioinformatics, 4(3), 365-381, 2007. 10.1109/TCBB.2007.70224
37. H. Chan, M. S. Mohamad, S. Deris, N. Zaki, S. Kasim, S. Omatu, J. M. Corchado, H. Al Ashwal, “Identification of informative genes and pathways using an improved penalized support vector machine with a weighting scheme, Computers in Biology and Medicine, 77, 102-115, 2016. 10.1016/j.compbiomed.2016.08.004
38. Tang and Y. Q. Zhang and Z. Huang and X. Hu and Y. Zhao, “Recursive Fuzzy Granulation for Gene Subsets Extraction and Cancer Classification, Trans. Info. Tech. Biomed., 12(6), 723-730, 2008. 10.1109/TITB.2008.920787
39. Du, K. Li, X. Li, M. Fei, “A novel forward gene selection algorithm for microarray data, Neurocomputing, 133(6), 446- 458, 2014. 10.1016/j.neucom.2013.12.012
40. de Schaetzen, C. Molter, A. Coletta, D. Steenhoff, S. Meganck, J. Taminau, C. Lazar, R. Duque, H. Bersini, A. Nowe, “A Survey on Filter Techniques for Feature Selection in Gene Expression Microarray Analysis, IEEE/ACM Transactions on Computational Biology and Bioinformatics, 9(4), 1106-1119, 2012. 10.1109/TCBB.2012.33
41. Chakraborty, “Simultaneous cancer classification and gene selection with Bayesian nearest neighbor method: An integrated approach, Computational Statistics & Data Analysis, 53(4), 1462-1474, 2009. 10.1016/j.csda.2008.10.012
42. Tang, Y. Q. Zhang, Z. Huang, “Development of Two-Stage SVM-RFE Gene Selection Strategy for Microarray Expression Data Analysis, IEEE/ACM Trans. Comput. Biol. Bioinformatics, 4(3), 365-381, 2007. 10.1109/TCBB.2007.70224
43. Tang, Y. Q. Zhang, Z. Huang, X. Hu, Y. Zhao, “Recursive Fuzzy Granulation for Gene Subsets Extraction and Cancer Classification, IEEE Transactions on Information Technology in Biomedicine, 12(6), 723-730, 2008. 10.1109/TITB.2008.920787
44. A. Mundra, J. C. Rajapakse, “SVM-RFE With MRMR Filter for Gene Selection, IEEE Transactions on NanoBioscience, 9(1), 31-37, 2010. 10.1109/TNB.2009.2035284
45. Ojeda, J. A.K. Suykens, B. De. Moor, “Low rank updated LS-SVM classifiers for fast variable selection, Neural Networks, 21(2), 437-449, 2008. 10.1016/j.neunet.2007.12.053
46. Ghosh, B. C. Dhara, R. K. De, “Selection of Genes Mediating Certain Cancers, Using a Neuro-fuzzy Approach, Neurocomput., 133, 122-140, 2014.
47. Sheet, A. Ghosh, S. B. Mandal, “Selection of Genes Mediating Human Leukemia, Using Boltzmann Machine, Advanced Computing and Communication Technologies: Proceedings of the 10th ICACCT, 83-90, 2018. 10.1007/978-981-10-4603- 2-9
48. Sheet, A. Ghosh, S. B. Mandal, “Identification of influential biomarkers for human leukemia – An Artificial Neural Network approach, International Journal of Soft Computing & Artificial Intelligence, 4, 27-32, 2016.
49. Ghosh, R. K. De, “Neuro-fuzzy Methodology for Selecting Genes Mediating Lung Cancer, Proceedings of the 4th International Conference on Pattern Recognition and Machine Intelligence, 388-393, 2011.
50. Sheet, A. Ghosh, S. B. Mandal, “Selection of genes mediating human leukemia, using an Artificial Neural Network approach, Third International Conference on Advances in Electrical, Electronics, Information, Communication and Bio-Informatics (AEEICB), 2010-2014, 2017. 10.1109/AEEICB. 2017.7972415
51. Narayanan, E.C. Keedwell, J. Gamalielsson, S. Tatineni, “Single-layer artificial neural networks for gene expression analysis, Neurocomputing, 61, 217-240, 2004. 10.1016/j.neucom.2003.10.017
52. Q. Wang, H. S. Wong, H. Zhu, T. T.C. Yip, “A neural network-based biomarker association information extraction approach for cancer classification, Journal of Biomedical Informatics, 42(4), 654-666, 2009. 10.1016/j.jbi.2008.12.010

(Click to view)

(Click to view)