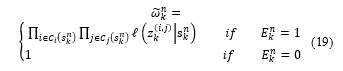Tracking and Detecting moving weak Targets
Volume 3, Issue 1, Page No 467–471, 2018
Adv. Sci. Technol. Eng. Syst. J. 3(1), 467–471 (2018);
 DOI: 10.25046/aj030157
DOI: 10.25046/aj030157
Keywords: Target Tracking, Track Before Detect, Detection, Particle Filter, Harvesting
Detect and tracking of moving weak targets is a complicated dynamic state estimation problem whose difficulty is increased in case of high clutter conditions or low signal to noise ratio (SNR). In this case, the track-before-detect filter (TBDF) that uses unthresholded measurements considers as an effective method for detecting and tracking a single target under low SNR conditions. In this paper, a particle filter based track-before-detect (PF-TBD) method is proposed to address the problem of detection and tracking with unthersholded data and a binary variable of the existence of the target for two motion models. Simulation results using image measurements based on TBD scenarios are also presented to demonstrate the capability of the proposed approach.
1. Introduction
The classical approach to target tracking is based on target measurements (position, range rate, and so forth) that are extracted by thresholding the output of a signal processing unit of a surveillance sensor [1].The primary role of thresholding is to reduce the data flow and thus simplify tracking. For a target of a certain signal-to-noise ratio (SNR), the choice of the detection threshold determines the probability of target detection and the density of false alarms. The false alarm rate, on the other hand, affects the complexity of the data association problem in the tracking system. In general, higher densities of false alarms require more sophisticated data association algorithms.
The undesirable effect of thresholding the sensor data, however, is that in restricting the data flow, it also throws away potentially useful information. For high SNR targets this loss of information is of little concern because one can achieve good probability of detection with a small false alarm rate. Recent developments of stealthy military aircraft and cruise missiles have emphasized the need to detect and track low SNR targets. For these dim (stealthy) targets, there is a considerable advantage in using the unthresholded data for simultaneous detection and track initiation [2], [3]. Depending on the type of sensor in use, the unthresholded data can be a sequence of range-Doppler maps, bearing-frequency distributions.
The concept of simultaneous detection and tracking using unthresholded data is known in literatures as track-before-detect (TBD) approach. Typically TBD is implemented as a batch algorithm using the Hough transform [4], dynamic programming [2] [3] or maximum likelihood estimation [5].
TBD algorithms based on the Hough transformation, dynamic programming or maximum likelihood methods are generally computationally intensive [6]. With recent advancement in Sequential Monte Carlo techniques, TBD algorithms implemented using PF are now computationally feasible [7] [8].
In this paper we also develop a recursive Bayesian TBD estimator; however, our formulation and implementation are based on the particle filter [7] [9]. The PF based TBD incorporates unthresholded data and a binary target existence variable into the target state estimation process. The presence and absence of target are explicitly modelled [10] [11]. This concept, allows us to calculate the probability of existence of the target directly from the filter.
The paper is organized as follows: section 2 the system dynamics and measurement model, are introduced for the TBD application. In section 3 formulates the TBD approach as a nonlinear filtering problem and describes the conceptual recursive Bayesian solution. The implementation of this solution using a particle filter is presented in section 4. In section 5 collects our simulations and results. Finally, we report our conclusions and direction for future research in section 6.
2. Formulation Problem
2.1. Dynamic Model
We assume that want to track a target moving in a 2-D plane with an unknown state vector at time step . We consider the state model given by:![]()
Where is the state transition matrix, assuming constant velocity motion and coordinate turn motion respectively, is the discrete-time index, is the process noise sequence, and is the state vector defined as:
![]() Here and denote the position, velocity, and the intensity of the target, respectively.
Here and denote the position, velocity, and the intensity of the target, respectively.
2.2. Transition Matrix
A target can be present or absent from the surveillance region at a discrete-time . Target presence variable is modelled by a two-state Markov chain, that is . Here denotes the event that a target is not present, while 1 denotes the opposite. Furthermore, we assume that transitional probabilities of target “birth” and “death” , defined as:
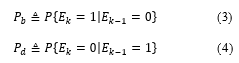 Are known, the other two transitional probabilities of this Markov chain, the probability of staying alive and the probability of remaining absent respectively, are given by:
Are known, the other two transitional probabilities of this Markov chain, the probability of staying alive and the probability of remaining absent respectively, are given by:
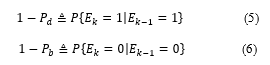 The corresponding transition matrix for the Markov process is:
The corresponding transition matrix for the Markov process is:
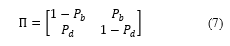 2.3. Sensor Model
2.3. Sensor Model
The sensor provides a sequence of two-dimensional images (frames) of the surveillance region, each image consisting of resolution cells (pixels). A resolution cell corresponds to a rectangular region of dimensions so that the center of each cell is defined to be at for and .
At each resolution cell the measured intensity is denoted as and modeled as:
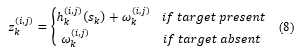 Where is the target contribution to intensity level in the resolution cell and is measurement noise in the resolution cell , assumed to be independent from pixel to pixel and from frame to frame. Thus for a point target of intensity at position , the contribution to pixel is approximated as:
Where is the target contribution to intensity level in the resolution cell and is measurement noise in the resolution cell , assumed to be independent from pixel to pixel and from frame to frame. Thus for a point target of intensity at position , the contribution to pixel is approximated as:
![]() Where is the amount of blurring introduced by the sensor. The complete measurements recorded at time a matrix denoted as:
Where is the amount of blurring introduced by the sensor. The complete measurements recorded at time a matrix denoted as:
![]() While the set of complete measurements collected up to time is denoted as usual: .
While the set of complete measurements collected up to time is denoted as usual: .
3. Bayesian Solution to TBD Filtering
The formal recursive Bayesian solution can be presented as a two-step procedure, consisting of prediction and update.
3.1. Prediction
The predicted target state can be written in terms of the target state and existence at the previous time, giving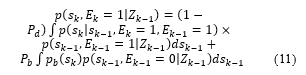
The pdf denotes the initial target density on its appearance.
3.2. Update
The update equation in the Bayesian framework is given by:
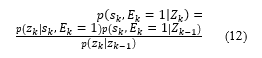 Where prediction density is given by (11) and is the likelihood function given by:
Where prediction density is given by (11) and is the likelihood function given by:
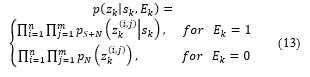 Here is the probability density function of background noise in pixel , while is the likelihood of target signal plus noise in pixel ,given that the target is in state , This two probability density function can be further expressed as:
Here is the probability density function of background noise in pixel , while is the likelihood of target signal plus noise in pixel ,given that the target is in state , This two probability density function can be further expressed as:
![]()
![]() Since the target (if present) will affect only the pixels in the vicinity of its location , the expression for can be approximated as follows:
Since the target (if present) will affect only the pixels in the vicinity of its location , the expression for can be approximated as follows:
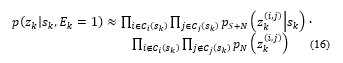 Where and are the sets of subscripts and , respectively, corresponding to pixels affected by the target.
Where and are the sets of subscripts and , respectively, corresponding to pixels affected by the target.
4. A Particle Filter for Track Before Detect (PF-TBD)
The recursive Bayesian solution of the track problem described in the previous section can be implemented using a particle filter [7] [9] [12] [13]has some similarities to the MMPF [14]. In this case we introduce the augmented state vector to include the existence variable. . Let us denote a random measure that characterizes the posterior probability density function at , namely , by .As usual, is the number of particles, while consists of and .The pseudocode of a single cycle of the PF developed for the TBD problem is presented in Table 1. The next step is the prediction of particle target states; this is done, however, only for those particles that are characterized by .For remaining particles (with , the target state components are undefined. There are two possible cases here:
4.1. Newborn Particles
This group of predicted particles is characterized by the transition from to .The target state particles are uniformly drawn at time step based on some a priori information on the minimum and maximum possible values on the target state.
4.2. Existing Particles
This group of particles that continues to stay “alive”, with to .The state transition model in equation (1) is used to update the target state particles.
The importance weights are computed next. For this purpose we need to introduce the likelihood ratio in pixel for a target in state , defined as:
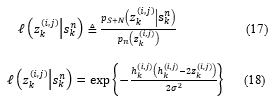 Where was defined in (9). Equation (18) follows from (14), (15), and (11). The importance weights (up normalizing constant) are now given by [7]:
Where was defined in (9). Equation (18) follows from (14), (15), and (11). The importance weights (up normalizing constant) are now given by [7]:
- Target existence transitions using the Regime Transition Algorithm given in [6]
RT
- FOR
- IF a newborn particle ( and )
Draw
- IF an existing particle ( and )
Draw
- Evaluate importance weight using (13)
- END FOR
- Calculate total weight: SUM
- FOR
- Normalize:
- END FOR
- Resample using systematic resampling algorithm given in [6]
RESAMPLE
The PF for track-before-detect performs target detection using the estimate of the posterior probability of target existence. This estimate is computed as:
![]() And satisfies . Target presence is declared if is above a certain threshold value. This declaration can then trigger the initialization of a track based on the estimated target state
And satisfies . Target presence is declared if is above a certain threshold value. This declaration can then trigger the initialization of a track based on the estimated target state
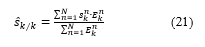 5. Simulation and Results
5. Simulation and Results
In the simulation we used two scenarios for target motion and random walk model is adopted for target intensity.
5.1. Scenario1
The first model is a nearly constant velocity model is used. The dynamic model [15] for the target can be described by (1).
Where and denote the level of process noise in target motion and intensity, respectively. A sequence of 30 frames of data has been generated with the following parameters:
The target is absent from frame 1 to frame 5 to be introduced in frame 6 with the initial intensity .The initial state is [6] [16] [17] .
The simulations are conducted under an initial intensity and , which corresponds to an SNR of and , respectively, according to the calculation equation . The target exists until frame 24 and is again absent in frames 25, 26,…, 30.
Figure 1 (a) and (b) show the measurement frame at time step 20 for dB and dB peak respectively.
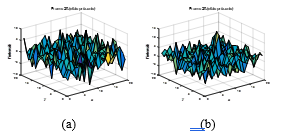 Figure.1: Measurements Frame (20): (a) for 6.71 dB Peak SNR, (b) for 12 dB Peak SNR for CV model.
Figure.1: Measurements Frame (20): (a) for 6.71 dB Peak SNR, (b) for 12 dB Peak SNR for CV model.
The particle filter parameters are selected as follows: transitional probabilities initial existence probability initial intensity range from to and number of particles. In figure (2) the probability of presence is shown for a SNR of 6.71 dB. Existence probability remains very stable and above 0.97 until frame 25.Then it drop sharply in frame 26, when the target is disappear.
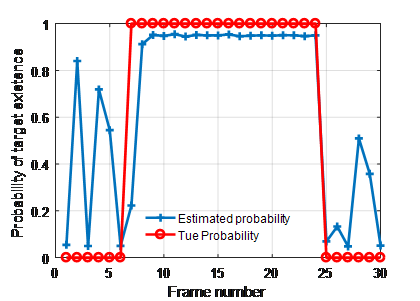 Figure.2: True and Estimated Target Existence Probability for SNR=6.71 dB
Figure.2: True and Estimated Target Existence Probability for SNR=6.71 dB
Figure (3) displays the true target path against the track, produced by the filter. Note how the target trajectory deviates slightly from the straight line due to process noise. The PF-TBD tracks the target with a small positional error.
 Figure.3: True and Estimated Target Trajectory for SNR=6.71 dB
Figure.3: True and Estimated Target Trajectory for SNR=6.71 dB
Figure (4) shows the position RMSE for three different peak SNR conditions (3.18 dB,6.71 dB, 12 dB). The position error is lower in 6.71 dB than 3.18 dB. As it can be seen, the PF-TBD was able to closely track the target even under low SNR.
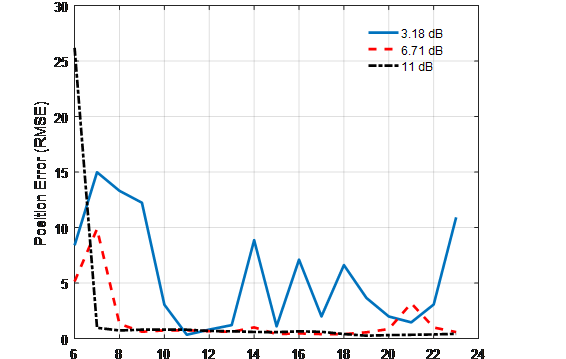 Figure.4: Position RMSE for the PF-TBD for differnet peak SNR
Figure.4: Position RMSE for the PF-TBD for differnet peak SNR
5.2. Scenario2
The second model is a Coordinate turn model is used [15]. The dynamic model for the target can be described by (1).
Figure 5 (a) and (b) show the measurement frame at time step 20 for dB and dB peak respectively.
 Figure.5: Measurements Frame (20): (a) for 6.71dB Peak SNR, (b) for 12dB Peak SNR for CT model.
Figure.5: Measurements Frame (20): (a) for 6.71dB Peak SNR, (b) for 12dB Peak SNR for CT model.
In figure (6) the probability of presence is shown for a SNR of 6.71 dB. Existence probability probability is still increase above frame 7 until frame 17 and still stable until frame 25. Therefore, it drops rapidly following the target disappears from the monitoring region after frame 25.
Figure (7) shows the true and estimated target trajectories for coordinate turn model, the estimated trajectory is very close to the true trajectory.
Figure (8) shows the position RMSE for three different peak SNR conditions (3.18 dB,6.71 dB, 12 dB). The position error is lower in 6.71 dB than 3.18 dB. As it can be seen, the PF-TBD was able to closely track the target even under low SNR.
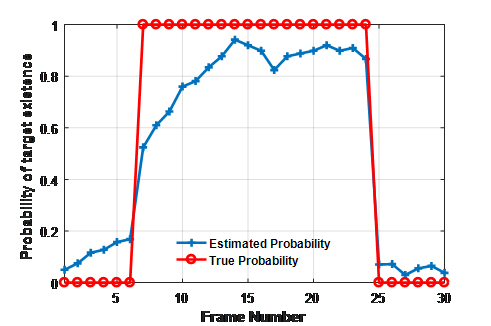 Figure.6: True and Estimated Target Trajectory for SNR=6.71 dB
Figure.6: True and Estimated Target Trajectory for SNR=6.71 dB
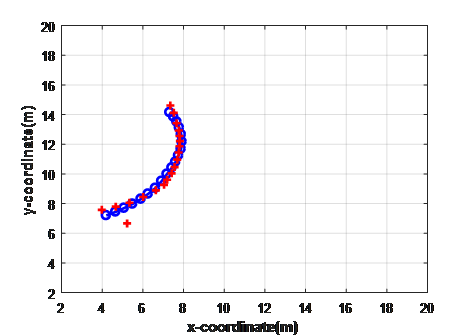 Figure.7: True and Estimated Target CT Trajectory for SNR=6.71
Figure.7: True and Estimated Target CT Trajectory for SNR=6.71
 Figure.8: Position RMSE for the PF-TBD for differnet peak SNR
Figure.8: Position RMSE for the PF-TBD for differnet peak SNR
6. Conclusion
In this paper, to manipulate moving weak targets, the PF-TBD algorithm is proposed for two dynamics models (CV and CT). The major advantage of the track-before-detect approach based on target existence variable and as a result, the developed particle filter can detect and track low SNR maneuvering target. The results from the simulation show that the PF-TBD algorithm has a successfully detection and tracking performance, both for constant velocity and coordinate turn models of moving targets, under severe conditions such as high noise or low SNR. Therefore, further work will mainly concentrate on how to detect and track multiple targets in high noise and high clutter.
- Blackman and R. Popoli, Design and Analysis of Modern Tracking System, Norwood: MA: Artech House, 1999.
- Barniv, Dynamic programming algorithm for detecting dim moving targets, in Multitarget Multisensor Tracking: Advanced Application (Y, Bar Shalom, ed),ch 4, Norwood: MA, Artech House, 1990.
- Arnold, S. Shaw and H. Pasternack, “Efficient target tracking using dynamic programming,” IEEE Trans Aerospace and Electronic Systems, vol. 29, pp. 44-56, January 1993.
- Carlson, E. D. Evans and S. L. Wilson, “Search radar detection and track with the Hough transform, part I: System concept,” IEEE Trans Aerospace and Electronic System, vol. 30, pp. 102-108.
- Tonissen and Y. Bar-Shalom, “Maximum likelihood track-before-detect with fluctuating target amplitude,” IEEE Trans, Aerospace and Electronic Systems, vol. 34, pp. 796-809, July 1998.
- Ristic, S. Arulampalam and N. Gordon, Beyond the Kalman Filter: Particle Filters for Tracking Applications, Boston: MA:Artech House, 2004.
- Salmond and H. Birth, “A particle filter for track-before-detect,” in Proc, Americain Control Conf, pp. 3755-3760, June 2001.
- Boyers and H. Drissen, “Particle filter based detection for tracking,” In Proceedings of the American Control Conference,, pp. 4393-4397, June 2001.
- Rollason and D. Salmond, “A particle filter for track-before-detect of a target with unknown amplitude,” in IEE Int, Seminar Target Tracking: Algorithms and Application, p. 14, October 2001.
- B. Colegrove, A. W. Davis and J. K. Alyliffe, “Track initiation and nearest neihbours incorporated into probabilistic data association,” Journal of Electrical and Engineers, vol. 6, pp. 191-198, September 1986.
- Musicki, R. Evans and S. Stankovic, “Integrated probabilistic data association,” IEEE Trans. Automatic Control, vol. 39, pp. 1237-1240, June 1994.
- J. Ballantyne, H. Y. Chan and M. A. Kouritzin, “A Novel branching particle method for tracking,” in Proc, SPIE, Signal and Data Processing of Small Targets,, vol. 4048, p. 287, 2000.
- G. Rutten, B. Ristic and N. J. Gordon, “A Comparison of Particle Filters for Recursive Track-before-detect,” in 7th International Conferenceon Information Fusion (FUSION), 2005.
- Mcginnity and G. W. Irwin, “Multiple Bootstrap Filter for Maneuvering Target Tracking,” IEEE Transaction of Aerospace and Electronic systems, vol. 36, no. 3, July 2000.
- Bar-Shalom, X. R. Li and T. Kirubarajan, Estimation with Applications to Tracking and Navigation, New York: Jhone Wiley&Sons, 2001.
- S. P and -S. A. P, “Generalized Recursive Track-Before-Detect With Proposal Partitioning for Tracking Varying Number of Multiple Targets in Low SNR,” IEEE Transactions on signal processing, vol. 64, no. 11, 2016.
- P. S and -S. P. A, “Generalized Recursive Track-Before-Detect With Proposal Partitioning for Tracking Varying Number of Multiple Targets in Low SNR,” IEEE Transactions on signal processing, vol. 64, no. 11, 2016.
- Amrouche, A. Khenchaf and D. Berkani, “Detection and Tracking Targets under Low SNR,” in IEEE International Conference on Industrial Technology, Toronto, 2017.
- Youssef Keryakos, Youssef Bou Issa, Michel Salomon, Abdallah Makhoul, "Introducing a Stress Management and Navigation System for Blind Individuals", Advances in Science, Technology and Engineering Systems Journal, vol. 10, no. 2, pp. 12–27, 2025. doi: 10.25046/aj100202
- Sarawuth Pramualsingha, Kazuo Yamamoto, RikutoTanaka, "Lightning Detection System for Wind Turbines Using a Large-Diameter Rogowski Coil", Advances in Science, Technology and Engineering Systems Journal, vol. 10, no. 1, pp. 1–6, 2025. doi: 10.25046/aj100101
- Abdennacer El-Ouarzadi, Anass Cherkaoui, Abdelaziz Essadike, Abdenbi Bouzid, "Hybrid Optical Scanning Holography for Automatic Three-Dimensional Reconstruction of Brain Tumors from MRI using Active Contours", Advances in Science, Technology and Engineering Systems Journal, vol. 9, no. 4, pp. 07–13, 2024. doi: 10.25046/aj090402
- Toya Acharya, Annamalai Annamalai, Mohamed F Chouikha, "Enhancing the Network Anomaly Detection using CNN-Bidirectional LSTM Hybrid Model and Sampling Strategies for Imbalanced Network Traffic Data", Advances in Science, Technology and Engineering Systems Journal, vol. 9, no. 1, pp. 67–78, 2024. doi: 10.25046/aj090107
- Ajla Kulaglic, Zeynep Örpek, Berk Kayı, Samet Ozmen, "Analysis of Emotions and Movements of Asian and European Facial Expressions", Advances in Science, Technology and Engineering Systems Journal, vol. 9, no. 1, pp. 42–48, 2024. doi: 10.25046/aj090105
- Toya Acharya, Annamalai Annamalai, Mohamed F Chouikha, "Optimizing the Performance of Network Anomaly Detection Using Bidirectional Long Short-Term Memory (Bi-LSTM) and Over-sampling for Imbalance Network Traffic Data", Advances in Science, Technology and Engineering Systems Journal, vol. 8, no. 6, pp. 144–154, 2023. doi: 10.25046/aj080614
- Koloud N. Alkhamaiseh, Janos L. Grantner, Ikhlas Abdel-Qader, Saad Shebrain, "Towards Real-Time Multi-Class Object Detection and Tracking for the FLS Pattern Cutting Task", Advances in Science, Technology and Engineering Systems Journal, vol. 8, no. 6, pp. 87–95, 2023. doi: 10.25046/aj080610
- Mai Ngoc Anh, "Simulation of Obstacle Detection Based on Optical Flow Images for Avoidance Control of Mobile Robots", Advances in Science, Technology and Engineering Systems Journal, vol. 8, no. 3, pp. 244–249, 2023. doi: 10.25046/aj080327
- Christoph Domnik, Daniel Erni, Christoph Degen, "Measurement System for Evaluation of Radar Algorithms using Replication of Vital Sign Micro Movement and Dynamic Clutter", Advances in Science, Technology and Engineering Systems Journal, vol. 8, no. 3, pp. 29–39, 2023. doi: 10.25046/aj080304
- Ivana Marin, Sven Gotovac, Vladan Papić, "Development and Analysis of Models for Detection of Olive Trees", Advances in Science, Technology and Engineering Systems Journal, vol. 8, no. 2, pp. 87–96, 2023. doi: 10.25046/aj080210
- Paulo Gustavo Quinan, Issa Traoré, Isaac Woungang, Ujwal Reddy Gondhi, Chenyang Nie, "Hybrid Intrusion Detection Using the AEN Graph Model", Advances in Science, Technology and Engineering Systems Journal, vol. 8, no. 2, pp. 44–63, 2023. doi: 10.25046/aj080206
- Habiba Sultana, A. H. M. Kamal, "An Efficient Way of Hybridizing Edge Detectors Depending on Embedding Demand", Advances in Science, Technology and Engineering Systems Journal, vol. 8, no. 1, pp. 63–77, 2023. doi: 10.25046/aj080108
- Roy D Gregori Ayon, Md. Sanaullah Rabbi, Umme Habiba, Maoyejatun Hasana, "Bangla Speech Emotion Detection using Machine Learning Ensemble Methods", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 6, pp. 70–76, 2022. doi: 10.25046/aj070608
- Lixin Wang, Jianhua Yang, Austin Lee, Peng-Jun Wan, "Matching TCP Packets to Detect Stepping-Stone Intrusion using Packet Crossover", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 6, pp. 13–19, 2022. doi: 10.25046/aj070602
- Rafia Akhter, Fred Beyette, "Detection of Event-Related Potential Artifacts of Oddball Paradigm by Unsupervised Machine Learning Algorithm", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 5, pp. 157–166, 2022. doi: 10.25046/aj070517
- Hassan Facoiti, Ahmed Boumezzough, Said Safi, "Computer Vision Radar for Autonomous Driving using Histogram Method", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 4, pp. 42–48, 2022. doi: 10.25046/aj070407
- Young-Jin Park, Hui-Sup Cho, "Lung Cancer Tumor Detection Method Using Improved CT Images on a One-stage Detector", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 4, pp. 1–8, 2022. doi: 10.25046/aj070401
- Ayoub Benchabana, Mohamed-Khireddine Kholladi, Ramla Bensaci, Belal Khaldi, "A Supervised Building Detection Based on Shadow using Segmentation and Texture in High-Resolution Images", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 3, pp. 166–173, 2022. doi: 10.25046/aj070319
- Hanae Naoum, Sidi Mohamed Benslimane, Mounir Boukadoum, "Encompassing Chaos in Brain-inspired Neural Network Models for Substance Identification and Breast Cancer Detection", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 3, pp. 32–43, 2022. doi: 10.25046/aj070304
- Haruka Motohashi, Hayato Ohwada, "Interpretable Rules Using Inductive Logic Programming Explaining Machine Learning Models: Case Study of Subclinical Mastitis Detection for Dairy Cows", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 2, pp. 143–148, 2022. doi: 10.25046/aj070214
- Mahdi Musa, Audu Mabu, Falmata Modu, Adam Adam, Farouq Aliyu, "Automated Hydroponic System using Wireless Sensor Networks", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 2, pp. 1–17, 2022. doi: 10.25046/aj070201
- Nganyang Paul Bayendang, Mohamed Tariq Khan, Vipin Balyan, "Thermoelectric Generators (TEGs) and Thermoelectric Coolers (TECs) Modeling and Optimal Operation Points Investigation", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 1, pp. 60–78, 2022. doi: 10.25046/aj070107
- Janusz Gurzynski, Lukasz Kajda, Marcin Tarasiuk, Tomasz Samotyjak, Zbigniew Stachowicz, Slawomir Kownacki, "Control and Monitoring Systems in Medium Voltage Distribution Networks in Poland – Current Status and Directions of Development", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 6, pp. 112–118, 2021. doi: 10.25046/aj060615
- Seok-Jun Bu, Hae-Jung Kim, "Ensemble Learning of Deep URL Features based on Convolutional Neural Network for Phishing Attack Detection", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 5, pp. 291–296, 2021. doi: 10.25046/aj060532
- Dmitry Petrov, Ulrich Hilleringmann, "Low-Power Primary Cell with Water-Based Electrolyte for Powering of Wireless Sensors", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 5, pp. 267–272, 2021. doi: 10.25046/aj060529
- Natasia, Sani Muhamad Isa, "Cyberbullying Detection by Including Emotion Model using Stacking Ensemble Method", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 5, pp. 229–236, 2021. doi: 10.25046/aj060525
- Osaretin Eboya, Julia Binti Juremi, "iDRP Framework: An Intelligent Malware Exploration Framework for Big Data and Internet of Things (IoT) Ecosystem", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 5, pp. 185–202, 2021. doi: 10.25046/aj060521
- Baida Ouafae, Louzar Oumaima, Ramdi Mariam, Lyhyaoui Abdelouahid, "Survey on Novelty Detection using Machine Learning Techniques", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 5, pp. 73–82, 2021. doi: 10.25046/aj060510
- Dunisani Thomas Chabalala, Julius Musyoka Ndambuki, Wanjala Ramadhan Salim, Sophia Sudi Rwanga, "Application of Geographic Information Systems and Remote Sensing for Land Use/Cover Change Analysis in the Klip River Catchment, KwaZulu Natal, South Africa", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 5, pp. 65–72, 2021. doi: 10.25046/aj060509
- Jianhua Yang, Lixin Wang, Yien Wang, "Enhance Student Learning Experience in Cybersecurity Education by Designing Hands-on Labs on Stepping-stone Intrusion Detection", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 4, pp. 355–367, 2021. doi: 10.25046/aj060440
- Shiwei Zhou, Jiayuan Gong, Leipeng Qie, Zhuofei Xia, Haiying Zhou, Xin Jin, "Driver Fatigue Tracking and Detection Method Based on OpenMV", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 3, pp. 296–302, 2021. doi: 10.25046/aj060333
- Nuraiza Ismail, Ermeey Abd Kadir, "A Rectification Circuit with Co-Planar Waveguide Antenna for 2.45 GHz Energy Harvesting System", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 2, pp. 984–989, 2021. doi: 10.25046/aj0602113
- Hoang Giang Vu, Thi Thuong Huyen Ma, "Observer-Based Method of Feature Extraction for the Fault Detection of Permanent Magnet Synchronous Motors", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 2, pp. 942–948, 2021. doi: 10.25046/aj0602107
- Binghan Li, Yindong Hua, Mi Lu, "Advanced Multiple Linear Regression Based Dark Channel Prior Applied on Dehazing Image and Generating Synthetic Haze", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 2, pp. 790–800, 2021. doi: 10.25046/aj060291
- Susanto Kumar Ghosh, Mohammad Rafiqul Islam, "Convolutional Neural Network Based on HOG Feature for Bird Species Detection and Classification", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 2, pp. 733–745, 2021. doi: 10.25046/aj060285
- Shahnaj Parvin, Liton Jude Rozario, Md. Ezharul Islam, "Vehicle Number Plate Detection and Recognition Techniques: A Review", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 2, pp. 423–438, 2021. doi: 10.25046/aj060249
- Adelaiye Oluwasegun Ishaya, Ajibola Aminat, Bisallah Hashim, Abiona Akeem Adekunle, "Improved Detection of Advanced Persistent Threats Using an Anomaly Detection Ensemble Approach", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 2, pp. 295–302, 2021. doi: 10.25046/aj060234
- Sk. Md. Masudul Ahsan, Aminul Islam, "Visual Saliency Detection using Seam and Color Cues", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 2, pp. 139–153, 2021. doi: 10.25046/aj060217
- Nasr Rashid, Khaled Kaaniche, "SIFT Implementation based on LEON3 Processor", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 1257–1263, 2021. doi: 10.25046/aj0601143
- Bryan Huaytalla, Diego Humari, Guillermo Kemper, "An algorithm for Peruvian counterfeit Banknote Detection based on Digital Image Processing and SVM", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 1171–1178, 2021. doi: 10.25046/aj0601132
- Antonio Vitale, Federico Corraro, Nicola Genito, Luca Garbarino, Leopoldo Verde, "An Innovative Angle of Attack Virtual Sensor for Physical-Analytical Redundant Measurement System Applicable to Commercial Aircraft", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 698–709, 2021. doi: 10.25046/aj060176
- Anass Barodi, Abderrahim Bajit, Taoufiq El Harrouti, Ahmed Tamtaoui, Mohammed Benbrahim, "An Enhanced Artificial Intelligence-Based Approach Applied to Vehicular Traffic Signs Detection and Road Safety Enhancement", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 672–683, 2021. doi: 10.25046/aj060173
- Alan A. Jorgensen, Las Vegas, Connie R. Masters, Ratan K. Guha, Andrew C. Masters, "Bounded Floating Point: Identifying and Revealing Floating-Point Error", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 519–531, 2021. doi: 10.25046/aj060157
- Aarthi Ramachandran, Amudha Joseph, Shunmuga Velayutham, "Feature Gate Computational Top-Down Model for Target Detection", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 1001–1006, 2020. doi: 10.25046/aj0506120
- Andrea Generosi, Silvia Ceccacci, Samuele Faggiano, Luca Giraldi, Maura Mengoni, "A Toolkit for the Automatic Analysis of Human Behavior in HCI Applications in the Wild", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 185–192, 2020. doi: 10.25046/aj050622
- Khalid Ait Hadi, Rafik Lasri, Abdellatif El Abderrahmani, "Inferring Topics within Social Networking Big Data, Towards an Alternative for Socio-Political Measurement", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 155–159, 2020. doi: 10.25046/aj050618
- Pamela Zontone, Antonio Affanni, Riccardo Bernardini, Leonida Del Linz, Alessandro Piras, Roberto Rinaldo, "Supervised Learning Techniques for Stress Detection in Car Drivers", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 22–29, 2020. doi: 10.25046/aj050603
- Mohammad Mohammad Abdul-Atty, Ahmed Sayed Ismail Amar, Mohamed Mabrouk, "C-Band FMCW Radar Design and Implementation for Breathing Rate Estimation", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 5, pp. 1299–1307, 2020. doi: 10.25046/aj0505156
- Redha Touati, Max Mignotte, Mohamed Dahmane, "A Circular Invariant Convolution Model-Based Mapping for Multimodal Change Detection", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 5, pp. 1288–1298, 2020. doi: 10.25046/aj0505155
- Paul Cabacungan, Carlos Oppus, Gregory Tangonan, Nerissa Cabacungan, John Paul Mamaradlo, Neil Angelo Mercado, "Design and Development of Electronic Sensor and Monitoring System of Smart Low-cost Phototherapy Light System for Non-Invasive Monitoring and Treatment of Neonatal Jaundice", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 5, pp. 1233–1246, 2020. doi: 10.25046/aj0505149
- Chunlai Yan, Hongxia Li, "Knowledge Mapping of Virtual Academic Communities: A Bibliometric Study Using Visual Analysis", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 5, pp. 493–499, 2020. doi: 10.25046/aj050561
- Hicham Moujahid, Bouchaib Cherradi, Oussama El Gannour, Lhoussain Bahatti, Oumaima Terrada, Soufiane Hamida, "Convolutional Neural Network Based Classification of Patients with Pneumonia using X-ray Lung Images", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 5, pp. 167–175, 2020. doi: 10.25046/aj050522
- Adonis Santos, Patricia Angela Abu, Carlos Oppus, Rosula Reyes, "Real-Time Traffic Sign Detection and Recognition System for Assistive Driving", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 4, pp. 600–611, 2020. doi: 10.25046/aj050471
- Katleho Moloi, Yskandar Hamam, Jacobus Andries Jordaan, "A Support Vector Machine Based Technique for Fault Detection in A Power Distribution Integrated System with Renewable Energy Distributed Generation", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 4, pp. 577–588, 2020. doi: 10.25046/aj050468
- Samir Allach, Mohamed Ben Ahmed, Anouar Abdelhakim Boudhir, "Deep Learning Model for A Driver Assistance System to Increase Visibility on A Foggy Road", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 4, pp. 314–322, 2020. doi: 10.25046/aj050437
- Amal Hadri, Khalid Chougdali, Raja Touahni, "Nonlinear \(\ell_{2,p}\)-norm based PCA for Anomaly Network Detection", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 4, pp. 234–243, 2020. doi: 10.25046/aj050429
- Rizki Jaka Maulana, Gede Putra Kusuma, "Malware Classification Based on System Call Sequences Using Deep Learning", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 4, pp. 207–216, 2020. doi: 10.25046/aj050426
- Ali Al-Rashid, "Composition of Methods to Ensure Iris Liveness and Authenticity", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 4, pp. 130–143, 2020. doi: 10.25046/aj050417
- Ruba Obiedat, "Risk Management: The Case of Intrusion Detection using Data Mining Techniques", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 3, pp. 529–535, 2020. doi: 10.25046/aj050365
- Akram Hatem Saber, Mohd Ayyub Khan, Basim Galeb Mejbel, "A Survey on Image Forgery Detection Using Different Forensic Approaches", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 3, pp. 361–370, 2020. doi: 10.25046/aj050347
- Jesuretnam Josemila Baby, James Rose Jeba, "A Hybrid Approach for Intrusion Detection using Integrated K-Means based ANN with PSO Optimization", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 3, pp. 317–323, 2020. doi: 10.25046/aj050341
- Manh Le Tran, Sunghwan Kim, "Enhanced Collaborative Constellation for Visible Light Communication System", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 3, pp. 259–263, 2020. doi: 10.25046/aj050333
- Sally Almanasra, Ali Alshahrani, "Alternative Real-time Image-Based Smoke Detection Algorithm", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 3, pp. 123–128, 2020. doi: 10.25046/aj050316
- Gillala Rekha, Shaveta Malik, Amit Kumar Tyagi, Meghna Manoj Nair, "Intrusion Detection in Cyber Security: Role of Machine Learning and Data Mining in Cyber Security", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 3, pp. 72–81, 2020. doi: 10.25046/aj050310
- Aditi Haresh Vyas, Mayuri A. Mehta, "A Comprehensive Survey on Image Modality Based Computerized Dry Eye Disease Detection Techniques", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 2, pp. 748–756, 2020. doi: 10.25046/aj050293
- Rabeb Faleh, Souhir Bedoui, Abdennaceur Kachouri, "Review on Smart Electronic Nose Coupled with Artificial Intelligence for Air Quality Monitoring", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 2, pp. 739–747, 2020. doi: 10.25046/aj050292
- Yeji Shin, Youngone Cho, Hyun Wook Kang, Jin-Gu Kang, Jin-Woo Jung, "Neural Network-based Efficient Measurement Method on Upside Down Orientation of a Digital Document", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 2, pp. 697–702, 2020. doi: 10.25046/aj050286
- Evan Kristia Wigati, Gede Putra Kusuma, Yesun Utomo, "Combination of Salient Object Detection and Image Matching for Object Instance Recognition", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 2, pp. 584–591, 2020. doi: 10.25046/aj050273
- C. Namrata Mahender, Ramesh Ram Naik, Maheshkumar Bhujangrao Landge, "Author Identification for Marathi Language", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 2, pp. 432–440, 2020. doi: 10.25046/aj050256
- Dr. Minal Moharir, Karthik Bhat Adyathimar, Dr. Shobha G, Vishal Soni, "Scapy Scripting to Automate Testing of Networking Middleboxes", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 2, pp. 293–298, 2020. doi: 10.25046/aj050238
- Nova Muhammad Ferlansyah, Suharjito, "A Systematic Literature Review of Vessel Anomaly Behavior Detection Methods Based on Automatic Identification System (AIS) and another Sensor Fusion", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 2, pp. 287–292, 2020. doi: 10.25046/aj050237
- Brian Meneses-Claudio, Witman Alvarado-Diaz, Avid Roman-Gonzalez, "Classification System for the Interpretation of the Braille Alphabet through Image Processing", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 1, pp. 403–407, 2020. doi: 10.25046/aj050151
- Cuong Van Nguyen, Toan Van Quyen, Anh My Le, Linh Hoang Truong, Minh Tuan Nguyen, "Advanced Hybrid Energy Harvesting Systems for Unmanned Aerial Vehicles (UAVs)", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 1, pp. 34–39, 2020. doi: 10.25046/aj050105
- Noor Syahirah Nordin, Mohd Arfian Ismail, Vitaliy Mezhuyev, Shahreen Kasim, Mohd Saberi Mohamad, Ashraf Osman Ibrahim, "Fuzzy Modelling using Firefly Algorithm for Phishing Detection", Advances in Science, Technology and Engineering Systems Journal, vol. 4, no. 6, pp. 291–296, 2019. doi: 10.25046/aj040637
- Farah Nadia Ibrahim, Zalhan Mohd Zin, Norazlin Ibrahim, "Eye Feature Extraction with Calibration Model using Viola-Jones and Neural Network Algorithms", Advances in Science, Technology and Engineering Systems Journal, vol. 4, no. 6, pp. 208–215, 2019. doi: 10.25046/aj040627
- Niranjan A, Akshobhya K M, P Deepa Shenoy, Venugopal K R, "EKMC: Ensemble of kNN using MetaCost for Efficient Anomaly Detection", Advances in Science, Technology and Engineering Systems Journal, vol. 4, no. 5, pp. 401–408, 2019. doi: 10.25046/aj040552
- Michael Santacroce, Daniel Koranek, Rashmi Jha, "Detecting Malicious Assembly using Convolutional, Recurrent Neural Networks", Advances in Science, Technology and Engineering Systems Journal, vol. 4, no. 5, pp. 46–52, 2019. doi: 10.25046/aj040506
- Antonio Fuduli, Pierangelo Veltri, Eugenio Vocaturo, Ester Zumpano, "Melanoma detection using color and texture features in computer vision systems", Advances in Science, Technology and Engineering Systems Journal, vol. 4, no. 5, pp. 16–22, 2019. doi: 10.25046/aj040502
- Yuto Yoshizawa, Yutaka Watanobe, "Logic Error Detection System based on Structure Pattern and Error Degree", Advances in Science, Technology and Engineering Systems Journal, vol. 4, no. 5, pp. 01–15, 2019. doi: 10.25046/aj040501
- Stephen Craig Stubberud, Kathleen Ann Kramer, Allen Roger Stubberud, "Estimation of Target Maneuvers from Tracked Behavior Using Fuzzy Evidence Accrual", Advances in Science, Technology and Engineering Systems Journal, vol. 4, no. 4, pp. 468–477, 2019. doi: 10.25046/aj040457
- Takahiro Ishizu, Makoto Sakamoto, Masamichi Hori, Takahiro Shinoda, Takaaki Toyota, Amane Takei, Takao Ito, "Hidden Surface Removal for Interaction between Hand and Virtual Objects in Augmented Reality", Advances in Science, Technology and Engineering Systems Journal, vol. 4, no. 4, pp. 359–365, 2019. doi: 10.25046/aj040444
- Sanae El Hassani, Hind El Hassani, Noureddine Boutammachte, "Overview on 5G Radio Frequency Energy Harvesting", Advances in Science, Technology and Engineering Systems Journal, vol. 4, no. 4, pp. 328–346, 2019. doi: 10.25046/aj040442
- Maryam Butt, Golshah Naghdy, Fazel Naghdy, Geoffrey Murray, Haiping Du, "Investigating The Detection of Intention Signal During Different Exercise Protocols in Robot-Assisted Hand Movement of Stroke Patients and Healthy Subjects Using EEG-BCI System", Advances in Science, Technology and Engineering Systems Journal, vol. 4, no. 4, pp. 300–307, 2019. doi: 10.25046/aj040438
- Priyamvada Chandel, Tripta Thakur, "Smart Meter Data Analysis for Electricity Theft Detection using Neural Networks", Advances in Science, Technology and Engineering Systems Journal, vol. 4, no. 4, pp. 161–168, 2019. doi: 10.25046/aj040420
- Sohail Akhtar, Adarsh Tandiya, Medhat Moussa, Cole Tarry, "An Efficient Automotive Paint Defect Detection System", Advances in Science, Technology and Engineering Systems Journal, vol. 4, no. 3, pp. 171–182, 2019. doi: 10.25046/aj040323
- Mohammad Ahmar Khan, Sarfraz Fayaz Khan, Taher Alawi Taher Barham BaOmar, Abdul Rahman Mohammed Aqeel Ba Omar, "Development & Implementation of Smart Vehicle Over Speeding Detector using IoT", Advances in Science, Technology and Engineering Systems Journal, vol. 4, no. 2, pp. 170–175, 2019. doi: 10.25046/aj040222
- Viorel Lupu, "Web Authentication: no Password; Listen and Touch", Advances in Science, Technology and Engineering Systems Journal, vol. 4, no. 1, pp. 84–92, 2019. doi: 10.25046/aj040109
- David Kondru, Mehmet Celenk, Xiaoping A. Shen, "State Estimation based Echolocation Bionics and Image Processing based Target Pattern Recognition", Advances in Science, Technology and Engineering Systems Journal, vol. 4, no. 1, pp. 73–83, 2019. doi: 10.25046/aj040108
- Zheng Xie, Chaitanya Gadepalli, Farideh Jalalinajafabadi, Barry M.G. Cheetham, Jarrod J. Homer, "Machine Learning Applied to GRBAS Voice Quality Assessment", Advances in Science, Technology and Engineering Systems Journal, vol. 3, no. 6, pp. 329–338, 2018. doi: 10.25046/aj030641
- Elena Basan, Alexander Basan, Oleg Makarevich, "Probabilistic Method for Anomalies Detection Based on the Analysis of Cyber Parameters in a Group of Mobile Robots", Advances in Science, Technology and Engineering Systems Journal, vol. 3, no. 6, pp. 281–288, 2018. doi: 10.25046/aj030636
- Satyam Paul, Raheleh Jafari, "Recent Advances in Intelligent-Based Structural Health Monitoring of Civil Structures", Advances in Science, Technology and Engineering Systems Journal, vol. 3, no. 5, pp. 339–353, 2018. doi: 10.25046/aj030540
- Jia-Jing Kao, Chun-Liang Lin, Chih-Cheng Huang, Hau-Shian Jian, "Contactless Power and Bidirectional Data Transmission via Magnetic Field", Advances in Science, Technology and Engineering Systems Journal, vol. 3, no. 5, pp. 226–234, 2018. doi: 10.25046/aj030528
- Mohammed Faeik Ruzaij Al-Okby, Sebastian Neubert, Norbert Stoll, Kerstin Thurow, "Development and Testing of Intelligent Wheelchair Controller for Quadriplegic Patients", Advances in Science, Technology and Engineering Systems Journal, vol. 3, no. 5, pp. 220–225, 2018. doi: 10.25046/aj030527
- Mohamed Zied Chaari, Mohamed Al-Kuwari, Rashid Al-Rahimi, Mongi Lahiani, Hamadi Ghariani, "Acquiring Wi-Fi Energy to Charge a Mobile Phone", Advances in Science, Technology and Engineering Systems Journal, vol. 3, no. 5, pp. 28–35, 2018. doi: 10.25046/aj030505
- Andre Dehne, Nantwin Moller, Thorsten Hermes, "MARWIN: Localization of an Inspection Robot in a Radiation exposed Environment", Advances in Science, Technology and Engineering Systems Journal, vol. 3, no. 4, pp. 354–362, 2018. doi: 10.25046/aj030436
- Mohamed Abd Elghany Khalifa, Amr Elsayed Emam, Mohamed Ibrahim Youssef, "Performance Enhancement of MIMO-OFDM Using Redundant Residue Number System", Advances in Science, Technology and Engineering Systems Journal, vol. 3, no. 4, pp. 1–7, 2018. doi: 10.25046/aj030401
- Naoki Kimura, Yuya Takeda, Yoshifumi Tsuge, "Agent Based Fault Detection System for Chemical Processes using Negative Selection Algorithm", Advances in Science, Technology and Engineering Systems Journal, vol. 3, no. 2, pp. 90–98, 2018. doi: 10.25046/aj030211
- Yi Yi Aung, Myat Myat Min, "An Analysis of K-means Algorithm Based Network Intrusion Detection System", Advances in Science, Technology and Engineering Systems Journal, vol. 3, no. 1, pp. 496–501, 2018. doi: 10.25046/aj030160
- Andrew Adib, Rached Dhaouadi, "Performance Analysis of Regenerative Braking in Permanent Magnet Synchronous Motor Drives", Advances in Science, Technology and Engineering Systems Journal, vol. 3, no. 1, pp. 460–466, 2018. doi: 10.25046/aj030156
- Himanshu Upadhyay, Hardik Gohel, Alexander Pons, Leo Lagos, "Virtual Memory Introspection Framework for Cyber Threat Detection in Virtual Environment", Advances in Science, Technology and Engineering Systems Journal, vol. 3, no. 1, pp. 25–29, 2018. doi: 10.25046/aj030104