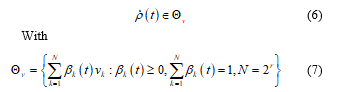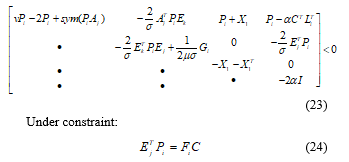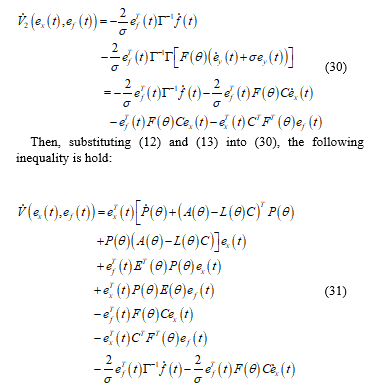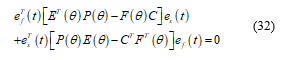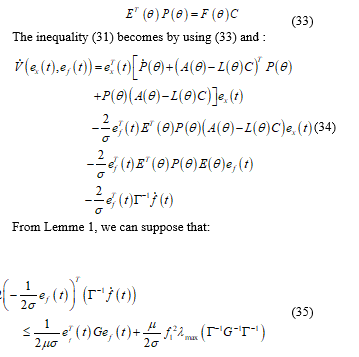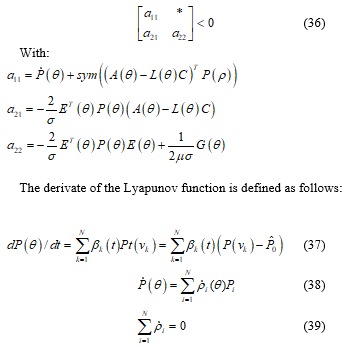1. Introduction

Research on fault detection, from a theoretical and experimental point of view, has been intensively developed during the last decades. All physical systems must operate normally and without anomaly. However, some conditions cause one or more faults in the process and interrupt this operation. So fault detection is an essential task to avoid degradation of system performance or even its damage [1].

The synthesis of observers for uncertain systems is based on the asymptotic stability of the error estimation equations or on the eliminating influence of uncertain perturbations and measurement of error on errors estimation. Linear Parameter varying system (also known as LPV system) is a special class of system that includes parameters-varying equations and parameters-varying state-space equations. These uncertain systems can be considered as a linearization of state-space nonlinear systems.

The polytopic LPV form is a special class of LPV systems. Indeed, it is a description of the system as a convex combination of sub-models defined by the vertices of a convex polytope [2] [3]. Subsequently, these sub-models are combined by convex weighting functions which give a global model. Similarly, [4] proposes a linear piecewise interpolation model of a diesel engine. The nonlinear model of the machine was transformed into an LPV model.

The synthesis of LPV observers is a direct extension of the LTI control methodologies [5]. The LPV theory has allowed to extend linear methods to nonlinear domains [6]. LPV modeling is used to study nonlinear systems, multiple models or switched models [7].

In this paper, the main contribution is a generalization of the obtained results for actuator fault reconstruction in [1] for LTI systems to continuous-time LPV systems. It was proved that linear methods could be extended to nonlinear domains [8] [9].  In this direction, the actuator fault reconstruction problem is articulated as an LMI feasibility problem. The existence of polyquadratic Lyapunov function could insure the stability of the error  estimation [10].

Due to the varying parameter, the polyquadratic approach considers that the Lyapunov function depends on the parameters associated with the description of the polytope.

The paper is organized as follows: In section 2 a model of linear polytopic time-varying (LPV) system is presented.  An adaptive observer for fault detection is described in section 3. In section 4, we introduce the polyquadratic adaptive observer for the polytopic LPV system which leads to less conservative conditions on terms of LMI.  The simulation result illustrates the effectiveness of our contribution.

Notation. For conciseness the following notations are used: ,

2. Problem Statements and Preliminaries

A continuous-time LPV system in presence of fault can be described by the state-space equations in the following form:

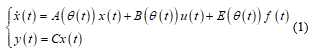Where ,  and  are, respectively, the state space, the input and the output vectors of the system. Variable  represents actuator fault.

The scheduling q is a set of varying parameters evaluated in hypercube domain Q such as:

Where and ,  are  the lower  and upper bounds of the parameter.

The parameter dependent Lyapunov function is assumed to be measurable [11] :

Furthermore, LPV system (1) can be defined via barycentric combination of a matrix polytope described by  vertices [12].

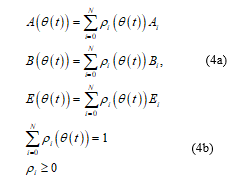Where ,  , are time invariant matrices defined for the ertex of the hypercube and . The weighting function  define the relative contribution of each vertices  to build the system described by .

2.1.  Assumption 1 [11]:

 The state-space matrices  are continuous and bounded functions and depend on .

2.2.  Assumption 2 [11]:

The real parameters  that can be known by on-line measurement values exist in LPV system and vary in a polytope  as:

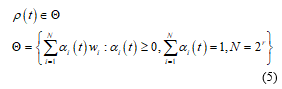And the rate of variation  are well defined at all times and vary in a polytope as:

The following assumption is made:

2.3.  Assumption 3:

Without loss of generality matrix  is considered full row rank.

2.4.      Assumption 4:

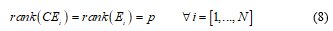2.5.  Assumption 5:

The triple matrix  is observable.

For simplicity, the time variable  of  will be omitted if no confusion is caused.

3. Adaptive Observer Design

For polytopic LPV system (1), an adaptive observer is described by the following state representation:

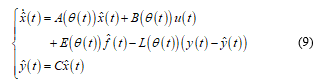Where ,  are the state and outputs estimated vectors and is the fault estimation.

In this case the gain matrix is given by the following polytopic form:

Where  represents the gain of   vertex.

Remark 1: Since it has been assumed that the pair  is observable, the gain matrices  can be selected such that  is stable.

Denote , ,  are respectively state  ,output  and fault estimations errors :

Then, the error dynamics are expressed as follows:

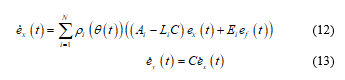The default is constant, hence  [13], consequently the derivate of    with respect to time can be written as:

The state observer (9) is combined with the law for the fault estimation updating of the form [1]

Where  and  is the learning rate.

It has been to note a modification of (13) is presented in [1], [6] for time varying  in the form:

Where  is a positive scalar and can guaranty  and .

4. Main Result

Consider the LPV system described by (1) with an additive fault. The choice of the parameter-dependent Lyapunov functions for polytopic systems is a dilemma in the literature. The rate of change of the scheduling parameter could be represented in diverse methods.  [14] proposed a rate of change that cannot be physically justified. Furthermore, in the expression given by [13], the derivative of the uncertain parameter does not impose special conditions.

In this section, we develop a new adaptive observer for LPV polytopic system.  Before, we introduce some instrumental tools which will be used in the proof of characterization of this observer.

4.1.  Lemma 1 [1]:

Given scalar  and symmetric positive definite matrix , the following inequality holds: 

4.2.  Lemma 2 [15]:

Given a symmetric matrix , and two matrices  of column dimensions , there exists  such that the following LMI holds:

If and only if the projection inequalities with respect to  are satisfied:

Where  and  denote arbitrary bases of the null spaces of  and  respectively.

Proof. See [15]. ■

4.3.  Lemma 3:

Let  a symmetric matrix and  matrices of appropriate dimensions. The following statements are equivalent:

• There exists a matrix such that:

Proof: The proof is obtained remarking that (19) can be developed as follows:

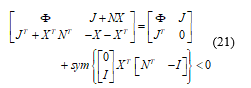and by applying Lemma 2 In this part, we consider the case such as the fault is time-varying, which implies , and the derivate of  with respect to time is:

The objective of this section is to propose an approach to design a new adaptive observer for polytopic LPV system (1). So, we propose the following Theorem 2.

Theorem 2.  Under the assumptions 1, 2 and 3, the system (9) is an adaptive observer for the system (1) if, for a given scalars , ,  and , there exists, for each vertex, asymmetric positive definite matrix , , and  such  that the following conditions hold:

Under constraint:

The gain observer matrix of the system (1) is given by the following polytopic form:

Remark 3: The principle of the polytopic formulation is based on the fact that the system and stability conditions (here in a LMI form) have affine dependence on the parameters. If, for some reason, the affine dependence is lost, the stability of the system is not equivalent (or even implied only) to the feasibility of the LMI at each vertex [16], [17], [18].

Proof: With respecting to the system parameter, it is clear that  is linear. Thereby, consider the Lyapunov polytopic function defined by:Where is a symmetric positive defined matrix.

Then, the derivative of (26) with respect to t is:

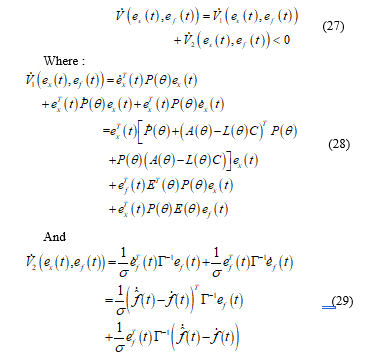Substituting (16) into (28) leads to :

If the following condition is introduced:

This implies that:

Then, subsisting (35) in (34), the following inequality is done:

The rate  can be represented in several ways. In fact most of the time, it is difficult to give adequate modeling of it. For LPV system, the derived parameter does not vanish as in the LTI case.

In our case, we suppose that [14]:

Unfortunately, (41) is not convex in  and , and cannot be solved by the LMI tools.

We can introduce some transformations to simplify the product term  of the inequality (41). In fact, in this solution we introduce an additive variable in order to allow the decoupling between the Lyapunov matrix and the observer gain in one side and to preserve a general structure to the Lyapunov matrix in the other side.

We suppose that:

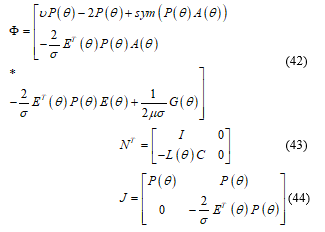By lemma 2 with (42), (43) and (44), there exists a matrix  of appropriate dimensions such that inequality (45) is satisfied.

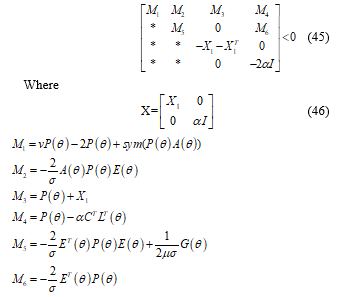Remark 4: The main advantage of problem (45) will appear when dealing with poly-quadratic observer. In that case, we will see that it theoretically improves the obtained results.

5. Numerical example

The above-described algorithm was applied to reconstruct the fault applied to the following LPV system described in [5] as:

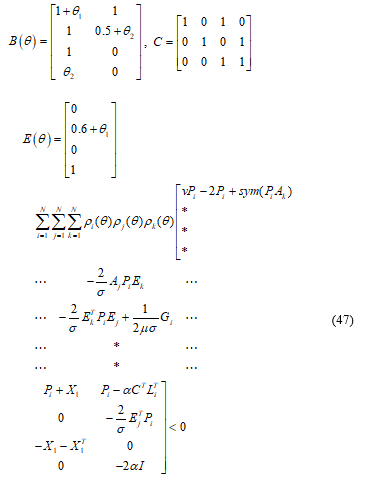The gain scheduling vector is defined as:

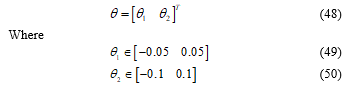The system has four vertices and evolves in a hypercube.  The weighting functions, which verified (4b), are computed as follows:

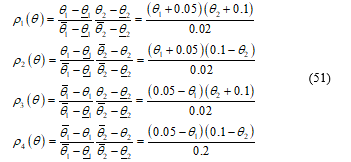The four local models represented the LPV system are calculated as the following:

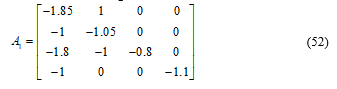
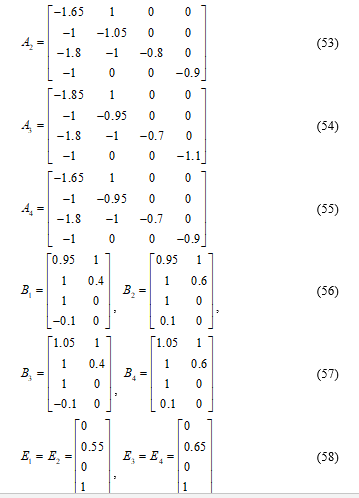By applying algorithm (9), gains matrices are as the following:

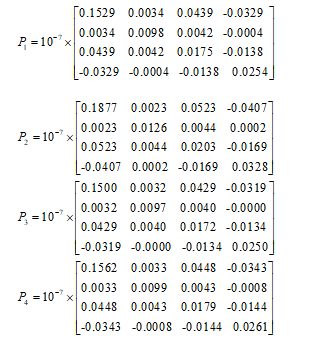The synthesis of the LPV observer gains  for each vertex is achieved with LMI Toolbox of Matlab. The observer gain  of the system described by (58) is determined offline using (9) in the different simulation case bellow. The parameters of simulation are fixed as .

To illustrate the effectiveness of our algorithm, we choose a particular system matrix  computed using (4) for arbitraries values of    and :

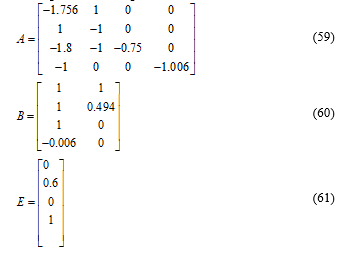  The given LPV system is defined in the vertex as shown in the figure above:

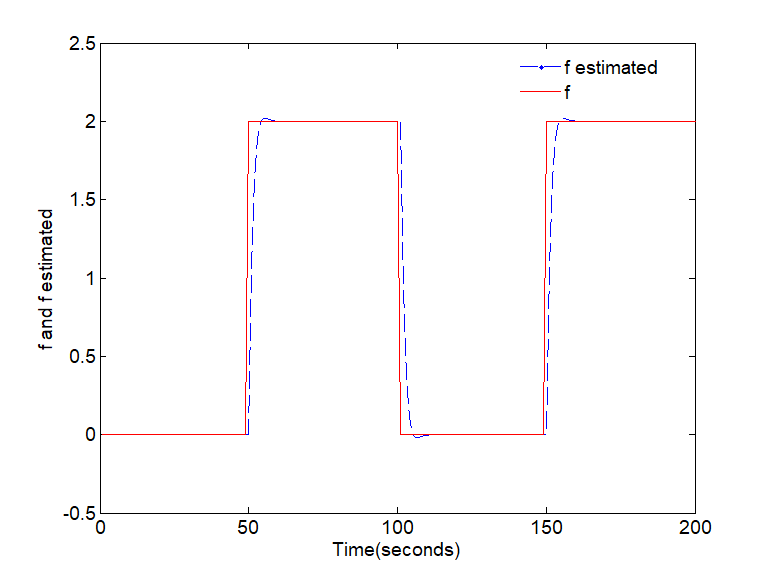
A.    Case of constant fault signal

In the first case, consider the constant fault described by the following equation:

Figure 1 and Figure 2 show the estimation of the fault applied to the system described by matrix (59), (60) and (61).

Fig. 1.   and its estimation .

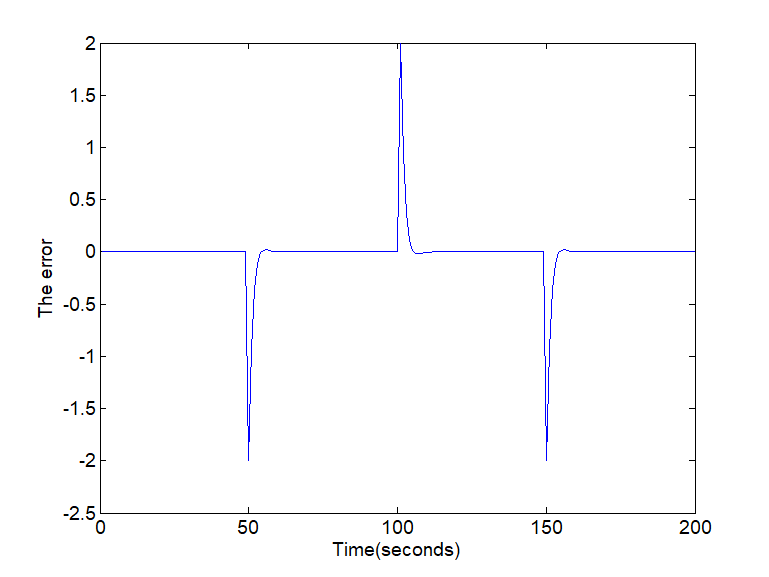Fig. 2.  The error  of the fault estimation

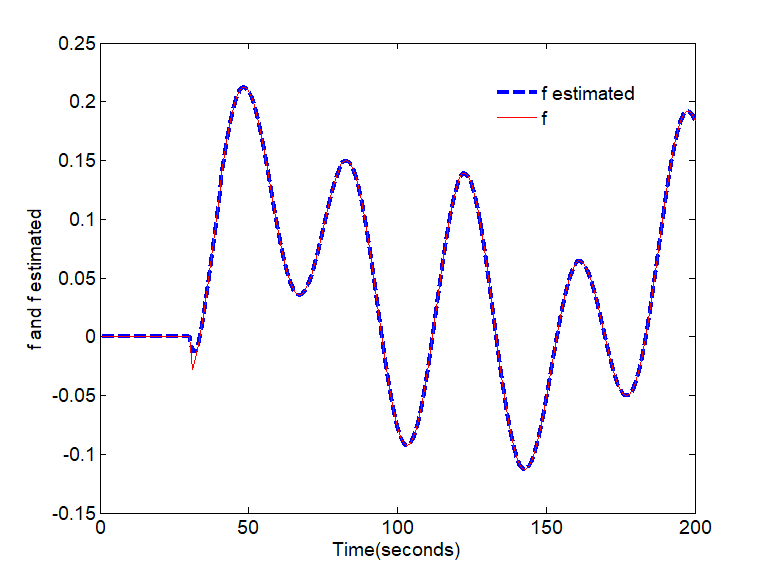
B.    Case of variable fault signal

The actuator fault is described by:

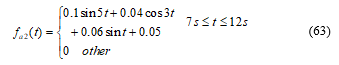For the arbitrary values of , the simulation results are as the following:

Fig. 3.   and its estimation .

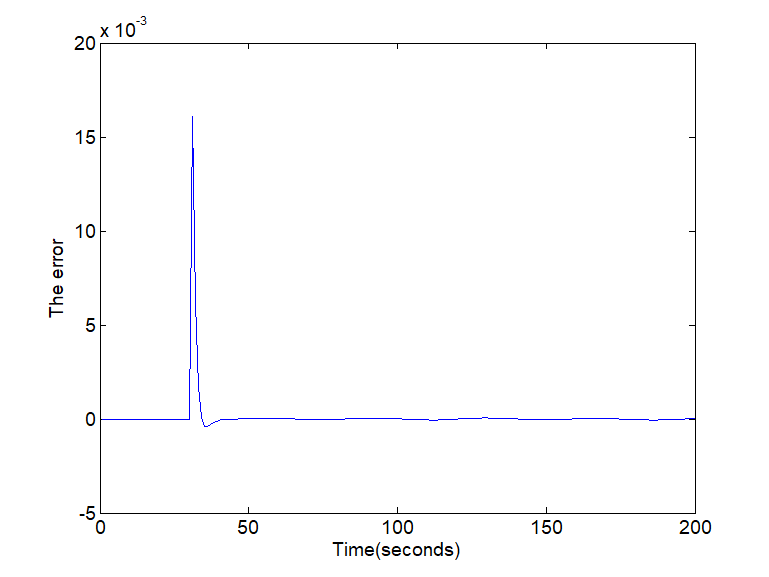Fig. 4.  The error   of the fault estimation

For the different types of fault signals considered above, Figure 2 and Figure 4 show the evolution of the error estimation. As can be observed, the error estimation converges asymptotic to zero even in the presence of disturbances. The real and the estimated constant and variable faults are displayed in Figure 1 and Figure 3 respectively. Summarizing, this approach can estimate the states and the fault functions with good performance and small error.

 6. Conclusion

In this paper, an adaptive LPV observer using LPV approach has been presented for a polytopic system. A constant fault and a variable fault were considered. A polyquadratic Lyapunov function was used to perform the stability analysis. The problem was formulated in terms of linear matrix inequalities to develop the observer. The simulation results show the performances of the proposed observer. The main advantage of this representation is that it doesn’t depend directly on the varying parameter. Moreover, this representation is defined as a difference between two parameters that evolve in two known and defined polytopes.

1. Zhang, B. Jiang and V. Cocquempot, “Adaptive Observer-based Fast Fault Estimation” International Journal of Control, Automation, and Systems, 6(3), 320-326, 2008.
   https://doi.org/10.1109/ChiCC.2015.7260636
2. M. Montes de Oca, D. Ayd?n, T. Stutzle, “An Incremental Particle Swarm for Large-Scale Continuous Optimization Problems: An Example of Tuning-in-the-loop (Re) Design of Optimization Algorithms”. Soft Computing, 15(11):2233–2255. https://doi.org/10.1007/s00500-010-0649-0
3. Grenaille, D. Henry and A. Zolghadri, “A method for designing fault diagnosis filters for LPV polytopic systems Journal of Control Science and Engineering. Volume 2008 (2008) : 1–11. http://dx.doi.org/10.1155/2008/231697
4. Changhui W, Zhiyuan L., “A LPV adaptive observer approach to calibrate MAF sensor map in diesel engine”. In: 54th Annual Conference of the Society of Instrument and Control Engineers of Japan (SICE), Hangzhou, China, pp.1375–1380. Piscataway, NJ: IEEE, 2015. https://doi.org/1109/SICE.2015.7285416
5. Hoffmann and H. Werner, “A Survey of Linear Parameter-Varying Control Applications Validated by Experiments or High-Fidelity Simulations”, IEEE Transactions on Control Systems Technology,Volume: 23, Issue: 2, pp. 416 – 433, 2015. https://doi.org/10.1109/TCST.2014.2327584
6. Bruzelius. “Linear Parameter-Varying Systems an approach to gain scheduling”. PhD thesis, Department Of Signals And Systems, Chalmers University of Technology, 2004.
7. Szászi, B. Kulcsár, G. J. Balas and J. Bokor, “Design of FDI filter for an aircraft control system”, Proceedings of the American Control Conference Anchorage, AK May 8-10, 2002. https://doi.org/10.1109/ACC.2002.1024596
8. Bruzelius, “Linear Parameter-Varying Systems: an approach to gain scheduling”, Phd thesis, University of Technology of Göteborg, February 2004.
9. Bruzelius, S. Pettersson and C. Breitholtz, “Linear parameter varying descriptions of nonlinear systems”, in Proceeding of the IEEE American Control Conference (ACC), pages 1374–1379, Boston, Massachusetts, July 2004.
10. Sename, P. Gáspár and J. Bokor, Robust Control and Linear Parameter Varying Approaches: Application to Vehicle Dynamics. Library of Congress Control, Number: 2012955946. Springer-Verlag Berlin Heidelberg, 2013.
11. Xie, “H2 gain scheduled state feedback for LPV system with new LMI formulation”, IEEE Proc.-Control Theory Appl., 152(6), November 2005.
12. Ichalal and S. Mammar, “On Unknown Input Observers for LPV Systems”, IEEE Transactions on Industrial Electronics, 2015. https://doi.org/10.1109/TIE.2015.2448055
13. Geromel and P. Colaneri, “Robust stability of time varying polytopic systems”, Systems and control letters, 55:81–85. 2006. https://doi.org/10.1016/j.automatica.2006.08.024
14. Caoand Z. Lin, “A Descriptor System Approach to Robust Stability Analysis and Controller Synthesis”, IEEE Transaction on automatic control, Vol. 49, No. 11, November, 2004. https://doi.org/10.1109/TAC.2004.837749
15. P. Boyd, L.E Ghaoui, E. Feron and V. Balakrishnam, Linear Matrix Inequalities in System and Control Theory, the Society for Industrial and Applied Mathematics, 3600 University City Science Center, Philadelphia, Pennsylvania 19104-2688, vol. 15, 1994.
16. Apkarian and R.J. Adams. “Advanced gain-scheduling techniques for uncertain systems”. IEEE Transactions on Automatic Control, 6:21–32, 1998. https://doi.org/10.1109/87.654874
17. Jungers, P.L.D. Peres, E.B. Castelan, E.R. De Pieri, and H. Abou-Kandil. “Nash strategy parameter dependent control for polytopic systems”. In 3^rd IFAC Symposium on Systems, Strcuture and Control, Brazil, 2007. https://doi.org/10.3182/20071017-3-BR-2923.00097
18. C. L. F. Oliveira, V. F. Montagner, P. L. D. Peres, and P.-A.Bliman. “LMI relaxations for H? control of time-varying polytopic systems by means of parameter dependent quadratically stabilizing gains”. In 3rd IFAC Symposium on System, Structure and Control, Foz do Iguassu, Brasil, 2007. https://doi.org/10.3182/20071017-3-BR-2923.00099

(Click to view)

(Click to view)