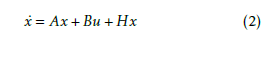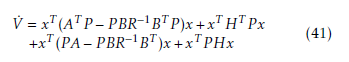1. Introduction

This paper is an extension of the work originally we presented in the International Conference on Advanced Systems and Electric Technologies, 2017 [1]. This work treats three approaches dealing with the decentralized control of interconnected systems.

In fact, large-scale interconnected systems have received considerable attention in recent years due to its presence in several fields such as power electronics, robotics, communication, aerospace, transportation networks, manufacturing processes, biochemical applications and others. Designing a centralized control for these systems may not be efficient due to the modular nature of the system that can prevent the sharing of information between the various subsystems. Thus it is important to decompose the largescale system into several subsystems. This decomposition which can be physical or mathematical, can make structures easier to control. This includes the implementation of decentralized control law.

In this way, it is necessary to decompose the global system into a number of interconnected subsystems for which, instead of a single centralized controller, a set of independent decentralized controllers is built. Thanks to its structure, the decentralized control has several advantages, mainly: the minimization of the information rate processed by the control units, the simplicity of the developed control laws compared to the centralized case and the improvement of the reliability of data transfer using only local information.

2. Many works in literature have been devoted

the decentralized control problems for interconnected systems. The decentralized adaptive control has been studied in [2–6]. The robust decentralized control is presented in [7–9]. The decentralized control using sliding mode approach is developed in [10–13].

Decentralized stabilization problem is the subject of our work. This problem is extensively studied in the literature and different design approaches were proposed accordingly [14–18]. To ensure the stability of the interconnected system formed by n subsystems, it is necessary to verify the local stability at each subsystem as well as the overall stability taking into account their interconnection.

The main contribution of this paper consists in developing some conditions allowing the synthesis of decentralized control laws that will ensure the stability of the overall interconnected system. In this way, we propose in this work a new decentralized stabilizing control approach for the interconnected systems. Indeed, the outcomes of this development are formulated in terms of linear matrix inequalities (LMIs).

The presented methods in our paper are applied to the physical system of two inverted pendulums interconnected by a spring. For the design of the decentralized control scheme, each pendulum should be seen as a subsystem. Many works used the typical system easily isolated into two subsystems to approve the validity of their proposed decentralized control approaches [19–22].

The rest of the manuscript is structured according to the following outline : The second section is reserved to formulate the problem and present the studied interconnected system formed by two parallel inverted pendulums coupled by a spring. In section 3, decentralized control approaches for the interconnected systems are presented, which are the decentralized quadratic optimal control and the decentralized pole-placement control. The last part of this section focuses on the development of a new decentralized stabilization control approach by using the Linear Matrix Inequalities Formulation. Section 4 is devoted to the implementation of the decentralized control approaches presented and developed in the previous section on the studied system. A comparative study between the three control approaches is presented to prove the validity of the new proposed approach. Finally, conclusions and some perspectives are given in the fifth section.

• Problem Formulation and Description of the Studied Dynamic System

2.1. Problem Formulation

Large-scale interconnected systems are represented as follows:

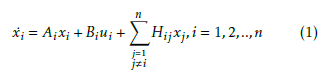where x_i ∈ IRⁿⁱ and u_i ∈ IRⁿⁱ denote the state vector and the control vector of i^th subsystem, respectively. A_i ∈ IR^ni×ni is the state matrix and B_i ∈ IR^ni×mi is the control matrix of each subsystem. H_ij represents the term of interconnection between the i^th subsystem and the other subsystems.

The global interconnected system composed of N subsystems can be rewritten in a compact form as follows:

where:

• x^T = [x₁^T ,x₂^T ,..,x_n^T ] is the state vector of the global system ;
• u^T = [u₁^T ,u₂^T ,..,u_n^T ] is the control vector of the global system ;
• A = diag[A_i],B = diag[B_i];
• H is the matrix formed by the terms of interconnection having the following form

2.2. Description of the Studied System : Double Inverted Pendulums Coupled by a Spring

We present in this section the description of the studied system formed by two interconnected inverted pendulum and its dynamic modeling.

In this system, two identical inverted pendulums of mass m directly mounted on the motor shafts in parallel where τ₁ and τ₂ are the input torques of each motor. These pendulums are connected to each other by an elastic spring of constant k which is mounted at the height a.

θ₁ and θ₂ are the angular displacements and of the pendulums from vertical.

New particular movements appear compared to the single movement of the individual pendulum. The interconnected inverted pendulums system is shown in figure 1 [23].

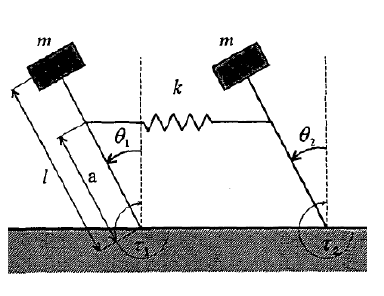Figure 1: Modeling of the parallel inverted pendulum

The Lagrangian is defined as the difference between the kinetic energies and the potential energies of the system.

The kinetic energy for each pendulum is described by the following form:

where J_i is the moment of inertia of the i^th pendulum and θ˙_i is the angular velocity of i^th pendulum.

The total kinetic energy of the global system is then:

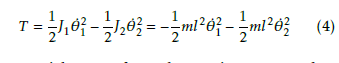The potential energy for each mass is represented as follows:

The potential energy of the spring is calculated using Hooke’s law:

The total potential energy of the system is given by:

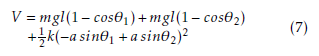The Lagrangian of the interconnected studied system is written as follow:

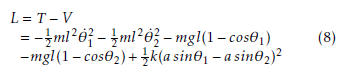⁻mgl(1⁻cosθ₂)+ ₂¹k(asinθ₁ ⁻asinθ₂)² The Euler-Lagrange equations are given by:

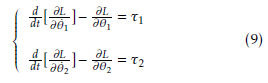Using Lagrange equations (9), we can easily show that the nonlinear equations of motion of the parallel inverted pendulum system are:

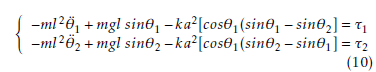Assuming a small angular displacement, the nonlinear equations of motion (10) can be replaced by the following linear model around the equilibrium point θ₁ = θ₂ = 0:

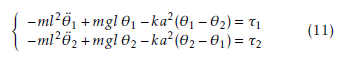So, the dynamics of the studied system composed of the two interconnected inverted pendulums are described by the following equations:

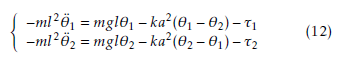For the design of the decentralized control scheme, each pendulum should be seen as a subsystem. Equations (12) can be writen into state equations with a standard choice of state variable for the i^th pendulum:

The system consisted of two interconnected inverted pendulums is then described by the following state equations:

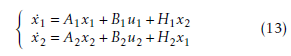• x₁,x₂ the state vectors of the subsystems ;
• u₁,u₂ the control vectors of the subsystem such as the input torque of each motor ;

The matrices and interconnection terms of the i^th subsystem are given by:

”        0 Ai =         g − ka2 l          ml2	1 #                    ” 0 # , B 0           i =     ml−12
” 0 Hi =          ka2	0 # , i = 1,2

The global system formed by two identical inverted pendulums coupled by a spring can be expressed by the following global state representation:

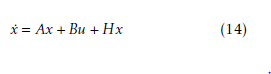m The mass of each pendulum, in Kg l The rod length, in m a The connecting position of the spring, in m k The stiffness of spring, in N/m g The acceleration of gravity, in m.s⁻² θ_i                   The angular displacement of the ith pendulum, in Rad

τ_i                The input torque of i^th motor, in N.m

3. Decentralized Control Approaches of Interconnected Systems

Possible control strategies for large-scale interconnected systems are generally based on a decentralized solution. A decentralized control structure applied to a process of n interconnected subsystems is shown in Fig 2.

The decentralized control partitions the measurement

information and elaborates a local and independent control law for each subsystem.

It is necessary to check the stability of the interconnected system by examining two main aspects:

• Local stability: at each subsystem.
• Overall stability: taking into account the interconnections.

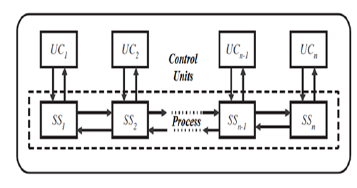Figure 2: Decentralized control structure

The synthesis of the decentralized controller consists in determining the local gains K_i which ensure the stability of the overall closed-loop system. To respect the decentralized information structure constraint, each subsystem is controlled by the local control law:

which leads to the following global control law of the overall system (2):

where K = diag(K₁,K₂,..,K_n) is the block diagonal control gain matrix. Using global state-feedbacks, we get the closed loop system dynamics as following:

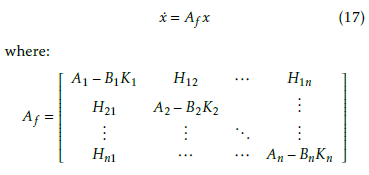To calculate the gains K_i, different approaches can be considered.

3.1. Decentralized Quadratic Optimal Control

The decentralized control synthesis consists in considering the decoupled subsystems defined by the following state equations:

and minimizing the modified quadratic criteria [24]:

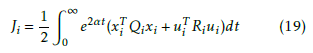Let Q_i(n_i × n_i),i = 1,..,n semi positive definite matrices, R_i(m_i×m_i),i = 1,..,n positive definite matrices and α a positive real.

The decentralized optimal control laws for each isolated subsystem can be expressed as a linear state feedback:

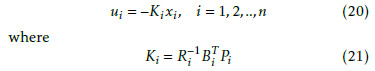and P_i is the symmetric positive definite matrix solution of the following algebraic Riccati equation:

These decentralized state feedbacks applied to the interconnected system lead to the following global state representation:

where R⁻¹ = diag[R⁻_i ¹] and P = diag[P_i].

A sufficient condition to guarantee the stability of the overall system taking into account the interconnections, is given by the following theorem which proof is detailed in Appendix A.

Theorem 1 [24]:

The decentralized control law (16) is globally and asymptotically stabilizable for system (17) if the matrix F, given by(24), is positive definite.

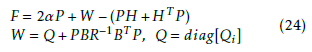3.2. Decentralized Pole-Placement Control

Pole-placement technique is a controller design method in which we determine the places of the closed loop system poles on the complex plane by setting a controller gain.

In this work we will apply this method for interconnected systems composed of n different subsystems that can be easily isolated. Firstly, it is necessary to verify the local stability.

For each subsystem, Ackermann’s formula is used to find the control gain matrices.

Theorem 2: Ackermann’s formula [25] The controllability matrix C can be formed from:

C = [B AB…Aⁿ⁻¹B]

The feedback matrix K can be found as:

K = [0 0…1]C⁻¹P_d(A) where P_d is the desired characteristic polynomial.

Using the local gain matrices obtained by Akermann’s formula for each subsystem, the matrix in closed loop A_f of the global system taking into account the interconnection is given by:

Stability condition:

In order to be stable, the eigenvalues of the system x˙ = A_f x must all lie strictly in the left half of the complex s-plane. That means, the eigenvalues must all have strictly negative real parts.

3.3. Synthesis of a Decentralized Stabilization Control

This section deals with the global asymptotic stabilization of linear interconnected systems within the framework of Linear Matrix Inequalities (LMIs). We present the development of a new decentralized control approach.

To compute the gain matrix K, so that the closed loop system (17) is asymptotically stable, let consider the quadratic Lyapunov function represented by the following form:

where P is a positive definite symmetric matrix of the following form:

The time derivative of V (x) is developped as :

The global asymptotic stability of system (17)provided with the decentralized control law (16) is ensured when the time derivative V˙ (x) is negative definite which is equivalent to:

Multiplying (28) on the right and then on the left by P ⁻¹ where P ⁻¹ is also symmetric positive definite matrix, inequality (28) becomes:

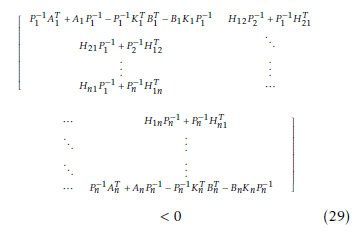It should be noted that the inequality matrix (29) has nonlinearities that are difficult to solve. We then use the changes of variables (30) and (31).

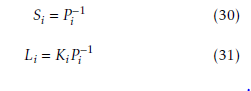Thus, the problem (29) can be rewritten to the form of linear matrix inequalities :

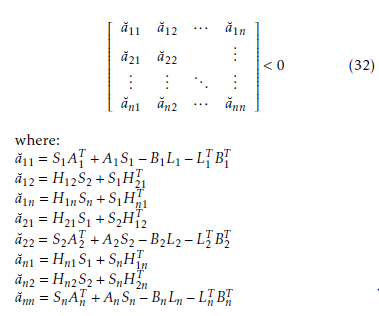a˘11 = S1AT1 +A1S1 −B1L1 −LT1 BT1 a˘12 = H12S2 +S1H21T a˘1n = H1nSn +S1HnT1 a˘21 = H21S1 +S2H12T a˘22 = S2AT2 +A2S2 −B2L2 −LT2 BT2 a˘n1 = Hn1S1 +SnH1Tn a˘n2 = Hn2S2 +SnH2Tn a˘nn = SnATn +AnSn −BnLn −LTn BTn

In order to find the gain matrices K of the decentralized control law, we have to solve the following LMI problem:

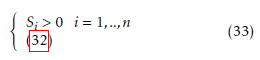The following result is proved::

The interconnected system (17) provided with the decentralized control law (16) is asymptotically stable if LMI problem (33) is feasible.

4. Simulation results

This section is devoted to the implementation of the three decentralized control approaches exposed and developed in the previous section.

It consists in studying the stability by decentralized quadratic optimal control, decentralized poleplacement control and decentralized stabilization control based on LMI applied to the interconnected inverted pendulums system (Figure1), presented in Section2. The parameters of the studied system are summarized in Table 1.

In last party of this section, we carry out a comparative study between these three studied decentralized approaches to confirm the validity and the efficiency of the proposed approach.

Parameter	Value	Unit
m	0.4489	Kg
l	0.325	m
a	0.21	m
k	340.22	N/m

Table 1: The studied system parameters

Using the numerical parameters, model (14) of interconnected system composed of two parallel inverted pendulums is given by:

To improve the performance of the studied system, we will apply the different studied approaches to guarantee an adequate stabilization.

4.1. Application of the decentralized optimal control approach

For this decentralized control, we focus on minimizing the modified quadratic criteria (19) for each separate pendulum.

The weighting factors are selected as follows:

The positive definite solution P_i of the Ricatti equation for each inverted pendulum is obtained by solving the equations (22):

” 0.0724 P1 =       0.0014	0.0014 # 0.0002
” 0.0725 P2 =       0.0014	0.0014 # (35) 0.0002

Using (20) and (21) we obtain the decentralized control gain matrices:

K1 = [−7.0068 −0.8247] K2 = [−7.0068 −0.8247]

To guarante the stability of the overall interconnected double-inverted pendulum, we should verify the theorem(24) when calculating the matrix F:

We can easily verify that matrix F is positive definite, so the decentralized control law stabilizes asymptotically the overall interconnected system (17).

The performances of the controlled system are shown in Figure3. The curves present the evolution of the system state variables with decentralized optimal control, when some perturbations occur on θ₁ and θ₂. From the simulation results shown in these curves, it can be seen that the decentralized optimal control is able to enhance stability of the studied system in approximately 0.6 seconds.

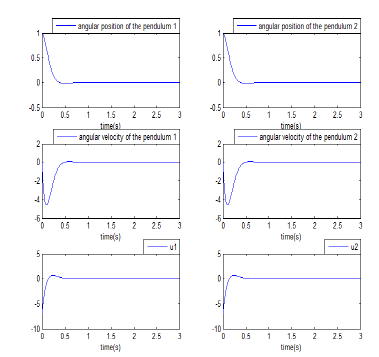Figure 3: Evolution of the system state variables and corresponding decentralized optimal control signals

4.2 Application of the decentralized poleplacement control approach

In order to apply the decentralized pole-placement for the studied interconnected system, we shall firstly decompose the system into two decoupled inverted pendulums.

Thus, the dynamical model of the isolated subsystems is given by:

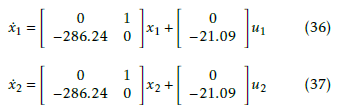Since both (A₁,B₁) and (A₂,B₂) are controllable, we can move their poles to any desired locations, we choose the following desired eigenvalues: λ¹₁ = −24;λ¹₂ = −18;λ²₁ = −24;λ₂² = −12

In this case we calculate the local gains using the Ackermann’s formula [25] :

K1 = [−6.9108 −1.9914]

K2 = [−0.0830 −1.7096]

Figures 4 and 5 present the evolution of the state variables and their corresponding pole-placement control signals for each isolated pendulum. From the simulation results shown in these curves, we can verify the local stability at each decoupled pendulum.

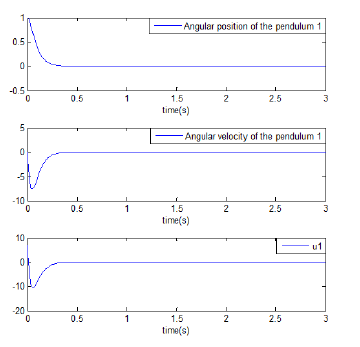Figure 4: Evolution of the state variables and corresponding pole-placement control signals for the first decoupled pendulum

Figure 5: Evolution of the state variables and corresponding pole-placement control signals for the second isolated pendulum

After having applied the formula of Ackermann for each isolated decoupled pendulum, we obtain the closed loop matrix A_f of the overall interconnected system.

The eigenvalues of the system (38) have strictly negative real parts:

λ1 =−0.9487 λ2,3 =−19.5639±17.0966i λ4 =−37.9236

Thus, the overall interconnected system provided with such a decentralized control law is asymptotically stable.

The curves in Figure6 illustrate the evolution of the system state variables and the corresponding decentralized pole placement control signals of the double inverted pendulum coupled by a spring, subjected to the same perturbations on the variable θ₁ and θ₂. From the simulation results shown in these curves, it can be seen that the decentralized control is able to enhance stability of studied system in approximately 4 seconds.

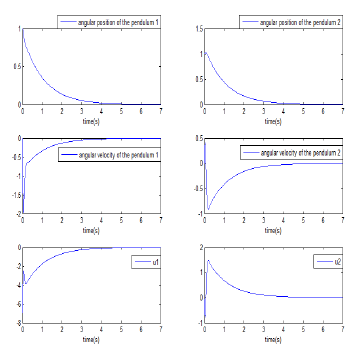Figure 6: Evolution of the system state variables and corresponding decentralized pole-placement control signals

4.3. Application of the decentralized stabilization control approach

We consider the application of the proposed decentralized stabilizing control developed in section 3.3. on the studied system formed by two inverted pendulums coupled by a spring.

In this part, we solve the proposed LMI formulation in order to find the decentralized gains of the double inverted pendulum. So we obtain:

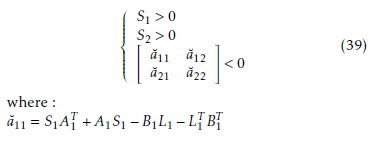a˘12 = H12S2 +S1H21T a˘21 = H21S1 +S2H12T a˘22 = S2AT2 +A2S2 −B2L2 −LT2 BT2

By solving problem LMI (39) we obtain the decentralized control gain matrices:

K1 = [−8.4386 −1.0841]

K2 = [−31.6377 −2.4752]

The evolution of the state variables of the dynamic system composed of two interconnected inverted pendulums with decentralized control by LMI is depicted in Figure 7.

It is clearly seen, from these curves, that the proposed decentralized stabilization control approach is efficient, it allows the best stabilization of the studied system despite the strong disturbances affecting the interconnection between its subsystems.

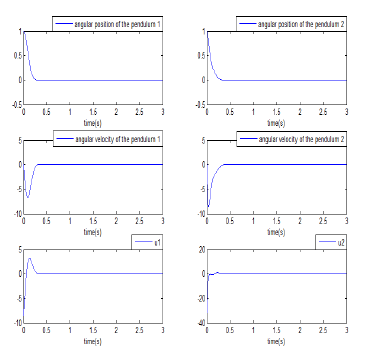Figure 7: Evolution of the system state variables and corresponding decentralized stabilizing control signals

4.4. Comparative study of the three approaches

We present in this section a comparative study between the three decentralized control approaches studied in section 3.

The visualization of the curves in figure 3, 6 and 7 presenting the evolution of the system state variables and the corresponding control signals, submitted to the same perturbations, shows that the three studied decentralized control approaches can improve the stability of the interconnected system with double inverted pendulums coupled by a spring.

However, we find some disadvantages when applying the decentralized quadratic optimal and decentralized pole-placement on interconnected system. We were obliged to decompose the overall system into a number of isolated subsystems and then to determine gain matrices that verify local stability for each subsystem. Then we present some sufficient conditions on the obtained gains to guarantee the global stability of the overall system taking into account the interconncetion terms. Indeed, we note an advantage for the proposed new stabilization decentralized approach using LMI problem which calculation of the local gains takes account of the interconnections terms.

On the other hand, when we compare the stabilization times of the three presented approaches, we note that our proposed approach is able to stabilize the system more quickly than other approaches.

5. Conclusion

This extended paper is devoted to the decentralized control techniques of large-scale interconnected systems. In this context, we have presented and studied some decentralized control approaches which objective is to synthesize the gains matrices in order to guarantee the stability of the global system. Our contribution focuses on the development of a new decentralized stabilization control approach based on linear matrix inequalities LMI.

The different approaches studied and formulated in this paper have been applied and validated on a double-parallel inverted pendulum coupled by a spring.

The simulation results have shown that it is possible to ensure the stability and improve the performance of the studied system controlled by each of the decentralized control laws relating to the proposed methods when some sufficient conditions are verified. Comparative study presented in the fourth section has confirmed the validity and the efficiency of the proposed approach based on LMI which succeeded to ensure quickly the stability of the system and calculated the local gains taking account of the interconnections terms.

Many interesting directions for future research remain. One of the possible perspectives is to develop decentralized control nonlinear approaches for multirobot cooperative system manipulating a common object.

Appendix A

The proof of the Theorem 1 is based on Lyapunov direct method. Let V be the Lyapunov function defined by the following quadratic form:

Using (23), The time derivative of V (x) is developped as :

So (41) becomes

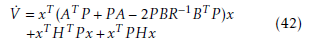Then, using the expression (22) in (42), we obtain:

To ensure the asymptotic stability of system (23) , V˙ should be negative definite, then which is equivalent to the matrix F:

should be positive definite.

1. Ben Amor, S. Elloumi, “On decentralized control techniques of interconnected systems-application to a double-parallel inverted pendulum” in International Conference on Advanced Systems and Electric Technologies(IC-ASET), Tunisia, 2017. https://doi.org/10.1109/ASET.2017.7983671
2. Wang, C. Wen, Y. Lin, W. Wang, “Decentralized adaptive tracking control for a class of interconnected nonlinear systems with input quantization” Automatica 81 (2017) 359-368, 2017. https://doi.org/10.1016/j.automatica.2017.03.010
3. Huang, J. Zhang, Z. Linc, “Decentralized adaptive controller design for large-scale power systems” Automatica 79 (2017) 93-100, 2017. https://doi.org/10.1016/j.automatica.2017.01.022
4. Wu, “Decentralised adaptive robust control schemes of uncertain large-scale time-delay systems with multiple unknown dead-zone inputs” IET Control Theory Appl., Vol. 11 Iss. 9, pp. 1360-1370, 2017. https://doi.org/10.1049/iet-cta.2016.1277
5. Sahami, M. U. Salamci, “Decentralized model reference adaptive control design for nonlinear systems; application to cancer treatment” in 17th International Carpathian Control Conference(ICCC), Slovakia, 2016. https://doi.org/10.1109/CarpathianCC.2016.7501173
6. Hernndez-Mndez, J. Linares-Flores, H. Sira-Ramrez, “Decentralized adaptive control for interconnected boost converters based on backstepping approach” in Energy Conversion Congress and Exposition (ECCE), USA, 2016. https://doi.org/10.1109/ECCE.2016.7854996
7. Wu, “Decentralised robust stabilisation of uncertain large-scale interconnected time-delay systems with unknown upper bounds of uncertainties” International Journal of Systems Science, 2015. https://doi.org/10.1080/00207721.2015.1029569
8. Rtibi, S. Elloumi, “Robust decentralized nonlinear control for multimachine power systems” in International Conference on Advanced Systems and Electric Technologies(IC-ASET), Tunisia, 2017. https://doi.org/10.1109/ASET.2017.7983739
9. Rtibi, S. Elloumi, N. Benhadj Braiek “A robust stabilization based on decentralized guaranteed cost control approach for a class of uncertain interconnected systems” in 4th International Conference on Systems and Control(ICSC), Tunisia, 2015. https://doi.org/10.1109/ICoSC.2015.7152782
10. J. Liu, “Decentralized Sliding Mode Control for Multi- Input Complex Interconnected Systems Subject to nonsmooth Nonlinearities” Asian Journal of Control, Vol. 20, No. 5, 2017. https://doi.org/10.1002/asjc.1627
11. Fathallah , F. Abdelhedi, N. Derbel, “A synchronizing second order sliding mode control applied to decentralized time delayed multiagent robotic systems: Stability Proof” Advances in Science, Technology and Engineering Systems Journal Vol. 2, No. 3, 160-170, 2017. https://doi.org/10.25046/aj020321
12. Abdelhedi, N. Derbel, “Adelay-dependent distributed SMC for stabilization of a networked robotic system exposed to external disturbances” Advances in Science, Technology and Engineering Systems Journal Vol. 2, No. 3, 513-519, 2017. https://doi.org/10.25046/aj020366
13. Cucuzzella, G. P. Incremona, A. Ferrara, “Decentralized Sliding Mode Control of Islanded AC Microgrids with Arbitrary Topology” IEEE Transactions on Industrial Electronics Vol. 64, Iss. 8, 2017. https://doi.org/10.1109/TIE.2017.2694346
14. Li, J. Li “Decentralized stabilization of fractional order TS fuzzy interconnected systems with multiple time delays” Journal of Intelligent and Fuzzy Systems 30 (2016) 319-331, 2016. https://doi.org/10.3233/IFS-151758
15. Lin, “Decentralized Stabilization of Uncertain Large-scale Fractional Order Interconnected Systems via Output Feedback” in American Control Conference (ACC), USA, 2016. https://doi.org/10.1109/ACC.2016.7525336
16. Liu, V. Gupta, “On Stabilization of Decentralized Systems Across Analog Erasure Links” IEEE Transactions on Automatic Control Vol. 62 Iss. 3, 2017. https://doi.org/10.1109/TAC.2016.2575833
17. Liu , D. Wang, H. Li, “Decentralized Stabilization for a Class of Continuous-Time Nonlinear Interconnected Systems Using Online Learning Optimal Control Approach” IEEE Transactions on Neural Networks and Learning Systems, 2014. https://doi.org/10.1109/TNNLS.2013.2280013
18. Bakule, M. de la Sen, M. Papik and B. Rehak, “Decentralized tabilization of symmetric systems with delayed observer-based feedback” in American Control Conference, USA, 2013. https://doi.org/10.1109/ACC.2013.6580888
19. Ferdowsi, S. Jagannathan, “Decentralized Fault Tolerant Control of a Class of Nonlinear Interconnected Systems” International Journal of Control, Automation and Systems 15(1) (2017) 1-10, 2017. https://doi.org/10.1007/s12555-015-0384-5
20. Zhao, D. Wang, G. Shi, D. Liu, Y. Li, “Decentralized control for large-scale nonlinear systems with unknown mismatched interconnections via policy iteration” IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2017. https://doi.org/10.1109/TSMC.2017.2690665
21. Zhao, D. Liu, Y.Li, Q. Wei, R. Song, “Adaptive Dynamic Programming Based Decentralized Tracking Control for Unknown Large-scale Systems” in Proceedings of the 36th Chinese Control Conference, China, 2017. https://doi.org/10.23919/ChiCC.2017.8027913
22. Wei, J. Luo, H. Dai, Z. Yin, J. Yuan, ‘Low-complexity differentiator-based decentralized fault-tolerant control of uncertain large-scale nonlinear systems with unknown dead zone”Nonlinear Dynamics , Vol. 89, Iss. 4, 2017. https://doi.org/10.1007/s11071-017-3605-z
23. S. Park, J.H. Kim, S.J. Kim, J.W. Choi, J.S. Kim, “Development of a Parallel Inverted Pendulum System and Its Control” in 38th SICE Annual Conference, Japan, 1999. https://doi.org/10.1109/SICE.1999.788676
24. S. Mahmoud, M.F. Hassan, M.G. Darwish, “Large scale control systems, theories and techniques” Edition Marcel Dekker, New York, 1985.
25. Ackermann, “Sampled-Data Control Systems” Springer- Verlag, Germany, 1985.

(Click to view)

(Click to view)