1. Introduction

The common thought about cars is that they are mechanical devices employed by passenger to move from a place to another. This is not true any more, or at least is not completely true since cars, or in general vehicles, in the last lustrum evolved to offer several services and connections that turn them into CyberPhysical Systems (CPS) by the combination of sensing/actuation, processing, storing, and networking capabilities, as described by Fortino et al. [1]. Applications, sensors, park and driving assistants are integrated into commercial vehicles and they are considered standard features present in entry-level model of cars. Features, such as Internet connectivity, enlarge the attack surface of vehicles and, in particular, traditional communication protocols developed to work on isolated environments could not maintain the same level of robustness when new variables are taken into account. This is especially true if one considers that connectivity itself can be provided in multiple heterogeneous ways, which are not always predictable by the manufacturer anymore. For example, in [2], the author proposed a connectivity solution based on smartphones. On the other hand, practically all Electronic Control Units (ECUs) on a car are connected to one or more CAN busses, which is the traditional interface for intra-vehicle communications. The CAN bus use messages whose payload is at maximum 64bits length, and depending on the payload set, it can enable specific functionality of the vehicle, for instance enabling the accelerator of a car. The CAN bus protocol was not designed to embed security properties such as: Authentication, Integrity and Confidentiality, and the security aspects are left to higher layers of the protocols-stack, for instance the application level. An example of attack on the CAN bus protocol is that performed on a Jeep Cherokee by Valasek and Miller in 2015 [3], where the authors showed how to hack and remotely control a Jeep Cherokee. This attack exploit a security flaw in the In-vehicle Infotainment (IVI) system of the car to access the CAN bus network of the car. To fix this flaw, the Fiat Chrysler was forced to push a software update [4].

Security issues are a major challenge for connected vehicles, as reported in [5], and this is recognised also to have a relevant impact on vehicle’s safety [6]; it is clear that security and safety are fundamental in the design of an intelligent transportation system, especially regarding the communication protocols and message protection schemes. It is important to note that the combination of safety and security issues is not exclusive of vehicular systems, but it affects the whole IoT world, especially systems which functionality is considered critical (e.g. medical devices).

In this work, we propose a solution to turn the CAN bus protocol as a Security by Design protocol by integrating authentication, integrity and confidentiality properties. Our solution proposes the adoption of a Message Authentication Code (MAC), targeted for CAN bus messages, that is then encrypted with an additional key. The message created guarantees authentication and integrity through the MAC, and confidentiality with the additional encryption. Our defence strategy is studied to be applied against a model of attacker that runs both a Honest-But-Curious (HBC) or Fully Malicious attack strategy. Furthermore, our solution is evaluated from a safety point of view, in particular regarding the residual probability of error (P_re). This is necessary since the outcome of the security MAC i.e. accept or reject a particular message is a form of error detection which could reveal also transmission errors (e.g. caused by noise), and the message containing the MAC could bring safety-critical information. For example, this scheme could be applied to SAE J1939 Torque/Speed Control 1 message, which embeds a 4-bit checksum within the 8-byte CAN payload. The residual probability of error is first evaluated using an ideal block cipher model, then simulation results are presented for a specific implementation choice. We show that averaging over the secret keys and over the possible messages, the value of P_re depends only on the length of the integrity tag used to decide whether the message is valid or not, and this is independent from how the integrity tag is generated. On the other hand, we show how the worst case combination of key and message reduces massively the ability of this scheme to detect transmission errors, assuming a simplified channel model. The worst-case P_re is then simulated, with considerations on the difficulty of finding the worst-case combination of key and message.

The main contributions of this paper is to analyse a message protection protocol from both a security and safety point of view, and highlight the trade-offs that result from the analysis. This paper is an extension of work originally presented in IEEE MT-ITS [7] and our contributions are summarized as follows:

• We improved the description of the analytical model for residual error probability by providing more details on the error model, new explanation on the computation of P_re and analytical results;
• We expanded the security analysis and we better modelled the attacker;
• We improved the safety analysis giving more details on the fragmentation and retransmission

issues;

• We added more results and better described the analytical model depending on the statistical distribution of errors in the simple case of binary symmetric channel;
• We redraw the plots with the simulation results, using colours, to be easier to understand.

This paper is structured as follows: section 2 reviews the state of the art with regard to MAC algorithms and best practices, as well as error detection mechanisms; section 3 presents the message protection scheme discussed in this paper, discussing some design choices. In section 4, we introduce the attacker model and we make a security consideration on the MAC size. Section 5 exposes two aspects usually relevant for the safety of the system, that are packet fragmentation and the probability of residual error P_re. Section 6 discusses other message protection schemes and their security and safety properties, compared to the scheme proposed here. Finally, section 7 concludes the paper with some motivation for future research directions.

2. Related Works

The following works refers to lightweight Message Authentication Code solutions for devices that have limited computational resources, like processors and memory. Chowdhury and Dasbit in [8] introduce LMAC, a Lightweight Message Authentication Code (MAC) of 64bits dimension for Wireless Sensor Network that uses hash based symmetric key MAC. The authors show that LMAC is secure against passive and active attacks and it has a low overhead compared with other similar solutions. Another 64bits MAC, called Chaskey is presented by the authors of [9]. Chaskey uses 128bits key to generate a MAC which length is of 64bits or more. The authors say that Chaskey generates MAC that are suitable for 32bit Microcontroller and that it does not suffer of MAC truncation [10]. In [11] the authors show two versions of lightweight MAC of 64 and 128bits called TuLP-64 and TuLP-128 that are resources efficient and are though for body sensor networks. Then, in [12] the authors presented a lightweight MAC suitable for Smart Grid communications in which two devices reach mutual authentication by sharing a session key exchanged using Diffie-Hellman and a hash-based authentication code technique.

Regarding safety properties, such as the residual probability of error, Schiller and Mattes have analysed different ways of using nested CRC codes, for example in [13]. However, when it comes to cryptographic algorithms the kind of errors treated are related to security properties and possible vulnerabilities, see for example the survey in [14]. To the best of our knowledge, an explicit model for the residual probability of error of a system using cryptographic algorithms has not been developed, although the statistical properties of symmetric ciphers are sometimes studied indepth, but always in the context of security, see for example [15].

3. Message protection scheme

The main scheme analysed in this paper is based on encryption, and is represented in Figure 1. In general, a message µ with length µ_size bits is combined with an integrity tag τ = H(k₂,µ) of length τ_size , where k₂ is the authentication key. The combined µ||τ is then encrypted to obtain the ciphertext c = ENC(k₁,µ||τ), where k₁ is the encryption key; the ciphertext is then transmitted on the CAN bus. The receiver receives c⁰, decrypts it and checks if τ⁰ = H(k₂,µ⁰), with µ⁰||τ⁰ = DEC(k₁,c⁰), to decide if the message is valid.

There can be some variations in this scheme; for example the integrity code can be appended to µ to form the plaintext (also known as MAC-then-encrypt approach) with c = ENC(k₁,µ||τ), or it can be excluded from encryption (encrypt-then-MAC approach) with c = ENC(k₁,µ)||τ. In both cases the MAC has to be computed using the original message µ. Sometimes the MAC-then-encrypt approach is considered less secure, for example see [16], but in this paper the scheme has no padding and a fixed length of the message, so these considerations do not apply. Considering the CAN bus, the first approach is more practical since there exist encryption algorithms with 64-bit block size, equal to the maximum payload of a CAN message; in this case there is no need for additional data to perform the encryption, and the ciphertext is computed as c = ENC(k₁,µ||τ). On the other hand, if the plaintext is different from the block size (like in the encrypt-then-MAC approach), the cipher must be used in counter mode, or a stream cipher can be used. Either way, there needs to be additional information shared between the sender and the receiver, e.g. a nonce, to perform the encryption; in this case the ciphertext is computed as c = ENC(k₁,I,µ)||τ with I being the shared information.

Another variant is to avoid the use of two different shared keys and define the integrity code as τ = H(µ), where H(·) is a hash function like SHA1 or an errordetection code of the CRC family.

In this paper we consider only different possibilities for the integrity tag τ = H(µ), which can be a proper Message Authentication Code, a hash function or a CRC; we do not consider then the encryptthen-MAC approach, so we can define the plaintext m = µ||τ.

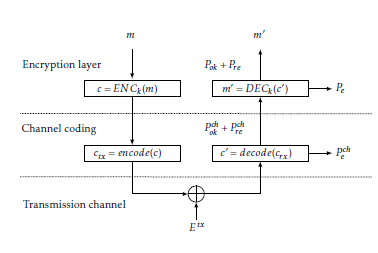Figure 1: Message protection scheme.

4. Security considerations

When cars were not connected to the Internet, the attack surface was limited to local entry points that could make cars vulnerable to security attacks. Since connectivity has been embedded as feature inside cars, the attack surface is increased and it is not limited to local attacks, but also remote ones make a vehicle more vulnerable. This provides a higher impact to the security and safety of cars’ passengers, and in addition, gives to attackers more and more kinds of attacks that they are able to exploit.

When, we talk about to local attacks, we refer to physical inputs to the vehicle that can be represented, for instance, by the auxiliary jack of the CD-Rom, USB ports, and the ODB2 connector. All these physical connectors require that an attacker has the opportunity to access the car and manipulate or alter the input to perform its attack. This, however, is possible but the impact is limited and less transparent to passenger. On the other side, remote attacks made on the wireless inputs enlarge the attack surface and may make attacks more relevant. Wireless inputs can be: the Bluetooth, Wi-Fi and cellular connections. In particular, exploiting the cellular connection, it would be possible to remotely access the In-vehicle infotainment (IVI) system of a car, and from that reading and writing into the CAN bus [3]. In fact, the IVI system are consoles that often run an operating system such as Windows CE, Linux, and may even run Android. So, attackers may exploit known vulnerabilities of unpatched version of those operating systems to perform their attacks. On this scenario, the Key Reinstallation Attacks (KRACKs) [17] has demonstrated that a vulnerability in the WPA2 protocol could allow “attackers to use this novel attack technique to read information that was previously assumed to be safely encrypted. This can be abused to steal sensitive information such as credit card numbers, passwords, chat messages, emails, photos, and so on^[1].”. Thus, using KRACKs and exploiting an unpatched version of the Wi-FI provided by the IVI, an attacker could jump in the car’s network getting sensitive information, and using that access as gateway to force and get in the CAN bus network of the vehicle.

4.1. Attacker Model

In this paper, we analyse the CAN protocol from the security and safety point of views. In particular, this section aims at modelling attackers, defining which are the attacks that they may exploit.

In the modelling phase, we consider that attackers may have local or remote access to the vehicle to compromise the CAN bus by forging or altering messages that may be considered valid by recipients. For instance, attackers may be able to exploit a weakness of the authentication module to remotely access the CAN bus network using a classic IP connection, and once inside the vehicle, they forge valid message or even altering their contents.

To minimize the power of attackers, our defence strategy foresees that more attackers are not able to forge valid messages, keeping enabled confidentiality of proper messages generated. Also, we aim at identifying messages that were altered, i.e., losing of integrity. Thus, our defence strategy is based on three security properties that are:

Authentication: A recipient should be able to verify whether a message is sent by a legitimate sender;

Integrity: A recipient should be able to verify whether a message has been altered during its transmission;

Confidentiality: it guarantees that the content of a message is not revealed to an illegitimate entity, as it can happen with the Man-in-the-Middle (MITM) attack;

We apply our defence strategy against attackers who can play the following roles:

Honest-but-Curious (HBC): Also known as Passive Attack; an attacker may exploit the information legitimately gleaned by capturing messages exchanged over the CAN bus network, but he/she will not perform any malicious activity to harvest it.

Fully Malicious (FM): Also known as Active Attack; an attacker is able to forge or alter messages that are considered valid, after a verification step, by the recipient. So, the attacker strategy is to succeed in at least one of the following attacks:

• Impersonation attack: the attacker is able to assume the identity of one of the legitimate parties;
• Guessing attack: the attacker is able to forge a valid MAC after a number of trials.
• Replay attack: the attacker is able to re-use valid messages with a malicious or fraudulent aim;
• Sniffing attack: the attacker is able to read the content of any messages exchanged through the CAN bus network:

In Table 1, we combine the defence strategy to each attack presented above aiming at blocking or mitigating the corresponding attack.

4.2. Security considerations on encrypted MAC and MAC size

We introduced the Message Authentication Code in the CAN-message payloads to provide by-design authentication and integrity properties. At the same time, by encrypting µ||τ, we added the confidentiality property in messages to avoid that an attacker sniffs content messages exchanged among ECUs. However, even not considering encryption on messages, but even only the first two properties, an attacker is capable to sniff messages, but she will not easily forge valid messages due to the MAC. With encryption, the attacker’s knowledge is still minor, and the probability to forge a valid message is linked to the guessing attack plus the encryption of µ||τ.

Dworkin in [18] points out the importance of choosing a robust MAC to be resistant against the guessing attack. In particular, Dworkin explains that a sound MAC is provided with a size greater than 64bits, i.e., τ_size ≥ 64-bits. However, due to the standard CAN bus payload restriction, i.e., 64bit in total, it is very hard to keep that inequality true and we need a workaround to guarantee the security properties with a specific level of risk. Thus, the workaround can be implemented through two different strategies:

5. i) concatenating a MAC which size is at least 64-bit, or ii) limiting the number of repeated trials of an attacker before considering invalid the key that generates the MAC. The first solution may cause the fragmentation issue that we detail better in §5.1. Instead, the second solution can be the best candidate for our workaround on τ_size. To this purpose, in [18], Dworkin illustrates how to calculate the right τ_size depending on the following two bounds:

MaxInvalids: as the limit on the number of trials that an attacker can perform before the key is retired;

Risk: the highest acceptable probability for an inauthentic message to be accepted as valid;

Then, due the above parameters, the τ_size should satisfy the following inequality:

MaxInvalids

Risk

Our goal is to satisfy the inequality 1 with a value of τ_size that is greater than or equal to 16. From inequality 1, the system can tolerate up to 30 (2⁵) messages before considering the key invalid, and the system can accept 2⁻¹¹, i.e., Risk = 2048, chance of inauthentic messages. So, considering that the payloadsize of a CAN-message is generically 48bits (µ_size) and the maximum bandwidth of the communication channel is 64bit (bandwidth_max), we obtain that µ_size + τ_size ≤ bandwidth_max. The inequality 1 defines that the lowest condition to have a µ||τ message for the CAN bus protocol is to have MaxInvalids = 2⁵ and Risk = 2048.

5. Safety considerations

5.1. Fragmentation

Attack Description Defence Impersonation Generating messages being identified as legitimate party Authentication Guessing Forging or altering messages that are valid by the recipient Confidentiality, Authentication, Integrity Replay Re-use messages that are considered valid by the recipient Authentication Sniffing Read content of messages Confidentiality Table 1: Summary of attack and defence strategies.

It is well known that a standard CAN message is too short for the proper implementation of many security properties, since the maximum allowed payload length is 8 bytes. However there are use cases where using a second CAN message (e.g. for authentication purposes) is not acceptable since it introduce unnecessary latency in the complete reception of a message; this is mainly due to the low speed of CAN bus, which is typically 250 kB/s on vehicular networks, and can reach the maximum of 1 MB/s. Another reason is the increase of residual error rate in the communication (see for example the appendix D.5.2 of ISO 15998 [19]); however, this increase could be tolerated more easily since, to a first approximation, the P_re of a twomessage scheme is roughly the double of the P_re of a single message. With these limitations, common application requirements allow for a rather limited security level achievable without changing the network communication protocol stack, and is fundamentally due, for a point-to-point communications, to the limited payload length of a single CAN 2.0 bus message. The use of CAN-FD could relax these limitations, but even in this case the maximum payload length is 64 bytes.

5.2. Retransmissions

In order to tolerate packet loss, communication protocols usually employ some form of re-transmission handling. Basically this means that if an error is detected on the packet, or if a timeout for packet reception expires, the transmitter sends again the same packet. Different variants of ARQ schemes (Automatic Repeat reQuest) exist, but the essential principle is that a data packet is sent more than one time without modifications. While this feature is usually handled transparently at link or transport layer, it is a potential security vulnerability, since an attacker could either inject errors or transmit duplicated packets to perform a replay attack (§4.1). Similar attacks are not hypothetical but have been demonstrated in reality, one of the most recent examples being the key reinstallation attack against WPA2 [17]. It is then desirable to handle retransmissions at the application level, if any, so sensitive security information like nonces, which must be used exactly one time, are handled properly. It is also worth considering that fragmentation makes retransmissions more complicated to handle efficiently, since here a small portion of a packet can be lost.

5.3.  Probability of Residual Error

The analysis of the probability of residual error P_re in a communication protocol is usually a difficult task. In order to simplify the model, it is assumed that the channel coding is independent from the encryption scheme and it is possible to obtain a measure of P_re for channel coding, which correspond to P_re^ch with reference to Figure 1. In this way, it is possible to focus only on the performance of the message protection scheme discussed in this paper. Here P_re is obtained assuming Shannon’s ideal cipher model, which has been used in other works like [20], and the results are compared with simulations where real algorithms are used for encryption and integrity.

5.3.1. Error model

According to Shannon’s model, an ideal cipher is a random family of permutations, chosen independently for each possible key. More precisely, suppose K is the set of all keys and M is the set of all messages.

An ideal block cipher is a map ENC : K × M → M where, for each key k ∈ K, the encryption function ENC_k(·) = ENC(k,·) is a random permutation on the message set M (independent of any other permutation). The same considerations apply to the decryption function DEC_k(·) = DEC(k,·), which being the inverse of a random permutation is itself a random permutation.

In this context, it is more useful to fix a specific pair (k,m) of key and message, and consider the cipher text message set as:

where the set E⁰ is the set of all possible undetected error vectors after channel decoding and before decryption, and E is the set of all error vectors after decryption. The addition here correspond to a bitwise XOR. While the elements of E⁰ correspond basically to undetected transmission errors, the elements of E can be seen as undetected transmission errors transformed by the decryption function. For this reason, the distribution of the values in E depends on the distribution of E⁰, in a different way for each different pair (k,m), since the function E(k,·) will correspond to a different and independent permutation. The relation between

E⁰ and E is then of the form ENC : K × M × E⁰ → E which can be rewritten as the map ENC_(k,m) : E⁰ → E identified by a specific pair of values (k,m). The explicit form can be derived from Figure 1 as

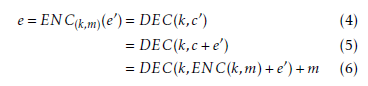Being ENC(k,·) and DEC(k,·) random permutations, equation 6 represent a random map from E⁰ to E. Each pair (k,m) correspond then to a different map ENC_(k,m), independent from other maps. This means that each error vector e⁰ on the transmission channel correspond to a random error vector e after decryption. Assuming that the pair (k,m) is chosen uniformly from the set K×M, the random error vector e is itself uniformly distributed. In practice, the relation between e and e⁰ is highly non-linear, since it strongly depends on the ENC and DEC functions, which in real block ciphers are usually highly non-linear functions themselves. This means that the approximation of uniform distribution of e, for any given e⁰ and varying (k,m), is accurate as long as these conditions apply:

1. the real block cipher approximates a random permutation;
2. the messages in M are uniformly distributed;
3. the keys in K are uniformly distributed.

Condition 1 is itself an important security property, as shown for example in [21]. Condition 2 can be false depending on the context; for example, in a closed industrial control network the message set is usually limited; furthermore, messages in M can include integrity checks (as in the scheme discussed here) which alter the distribution of the plaintext. Condition 3 is another important security property, although some block ciphers have weak keys (e.g. DES and Blowfish). These conditions can be relaxed to having either the messages or the key uniformly distributed, provided that condition 1 still apply.

5.3.2.  Computation of P_re

In this section, we assume these conditions are satisfied. Given that, as shown in section 3, the original message is m = µ||τ, and the received message is m⁰ = µ⁰||τ⁰, the probability of residual error can be defined as the joint probability

which correspond to the probability of having a correct integrity tag (τ⁰ = H(µ⁰)) but the decoded message is different from the original (µ , µ⁰) due to transmission errors. Considering that ENC_(k,m) is a random map, each element of C⁰ can correspond to all the possible values of M⁰. If the elements of C⁰ are uniformly distributed (such as when considering a random message attack) the probability that τ⁰ = H(µ⁰), averaged over all the possible (k,m), can be computed by counting as avg(τ0 = H(µ0)) = 2µ2sizeµsize+τsize = 2τ1size (8) P

which is the probability of guessing a valid message. On the other hand, when transmission errors are considered, only one of the elements of C⁰ correspond to the correct message, while all other elements have cumulative probability P_re^ch. The residual probability of error in this case can be computed as

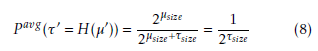
Both equations 8 and 9 are valid without making any assumption on the actual algorithm H used for computing τ.

This measure of P_re is, however, a measure for the average case, while from the safety point of view it is necessary to consider the worst case, that is:

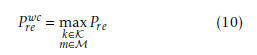This again can be computed by counting, but this time the actual distribution of E, given by transmission errors, must be considered, specifically the one which maximise equation 10, which correspond to the worstcase pair (k^wc,m^wc). Using the ideal cipher model, the distribution in E can be obtained from a permutation of the distribution in E⁰, so a simpler way to compute P_re^wc is to take the 2^µsize − 1 error vectors of E⁰ with higher probability P_e0 and sum their probability. Clearly, the upper bound for the various E is

where equality would mean that the encryption procedure, even with an integrity check, is not effective at all in detecting transmission errors when (k^wc,m^wc) are used, because the relevant transmission errors e cause the plaintext to have an non-correctable error. More specifically, this correspond to the case where the 2^µsize − 1 most probable error vectors in E cover practically the whole amount of P_re^ch. The fact that this is independent from the particular algorithm H is because of the random map; in other words it is impossible to design an efficient integrity algorithm for this scheme as the distribution of e can not be known a priori.

This consideration exposes the trade-off between safety (as related to protection against random errors) and security (as related to protection against a malicious adversary). In the first case the statistical distribution of transmission errors is usually concentrated on a restricted set of values, and error detection codes are designed to detect the most probable errors, achieving a very high detection rate. On the other hand, if a malicious adversary is considered, all error patterns must be distributed ideally uniformly, otherwise an attacker may exploit its statistical characteristics.

5.3.3. Analytical results

To illustrate this problem, we consider a simplified model with a binomial distribution E⁰ ∼ B(n,k,p) (which would correspond in Figure 1 to the case with no channel coding and a Binary Symmetric Channel with probability of bit error p). The worst case P_re^wc can then be obtained by first listing the probability P_l of each error vector e_l⁰ with l bit set (note that must be l > 0); this list is then sorted incrementally and then the first values are taken, one error vector at a time, until exactly 2^µsize − 1 error vectors are chosen. As shown in figure 2, where the worst-case residual probability of error is computed with the algorithm exposed above for different values of p in a binomial distribution, the value of P_re rapidly increases as the distribution of errors is more concentrated. Here τ_size is fixed to 64 bytes; similar results are obtained for different values. In figure 3 instead, µ_size is fixed to 256 bits and the worst-case P_re is plotted, and here the effect of the concentration of error distribution is also visible with effects similar to figure 2. This algorithm can be extended to the case where channel coding allows approximating the residual error distribution, for example if a CRC with a known minimum hamming distance H_CRC is used (some examples are available from the work of Koopman, see [22], for different payload lengths). In this case, the error vectors e_l with l < H_CRC are not considered since they are detected by channel coding. However if channel coding include other information in the CRC (such as the length of the data payload) this approximation must be further refined.

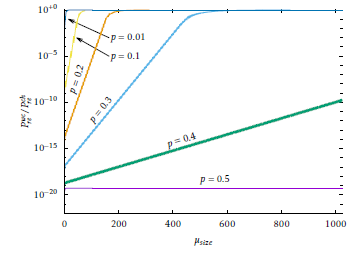Figure 2: Normalised worst-case P_re obtained through computation, for different values of p. τ_size is fixed to 64 bytes.

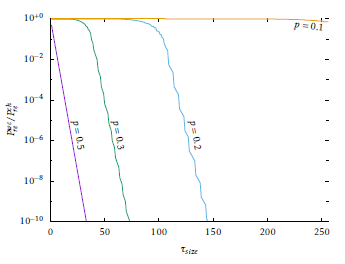Figure 3: Normalised worst-case P_re obtained through computation, for different values of p. µ_size is fixed to 256 bytes.

5.3.4.  Simulation results

The simulations have been performed applying the encryption scheme to randomly selected (k,m) and using different error vectors to obtain an approximation of P_re. For the ENC cipher, DES and AES have been used, while for H we used CRC, a truncated SHA1 hash function and a truncated HMAC scheme based on SHA1. The simulation have been implemented as a C++ program using the Nettle v2.7.1 cryptographic library. The simulations were run on a Intel i7 8-core laptop with 8 GB RAM; for each pair (k,m) a number of error patterns e⁰ are generated, with the respective probability, and the normalised output P_re is computed as the ratio between the erroneous messages that resulted in τ = H(µ) and the total number of erroneous messages. The plotted results represent a normalised P^Pre^re_ch , where the value of 1 represent equality in equation 11. The value of τ_size varies from 0 to 16; greater values, which in theory correspond to a lower P_re, have not been simulated since they would have taken too much time to yield a result with reasonable precision; however the results are still meaningful with respect to the theoretical model. The complexity of the simulation has three factors: k, m and e⁰. For example, using 1000 different keys, 1000 different messages and 10000 error patterns the total number of iterations is 1000 · 1000 · 10000 = 10¹⁰. However each value of P_re is evaluated using 10000 samples, so lower values close to 10⁻⁴ will have a lower accuracy. This explains the convenience to simulate with low τ_size.

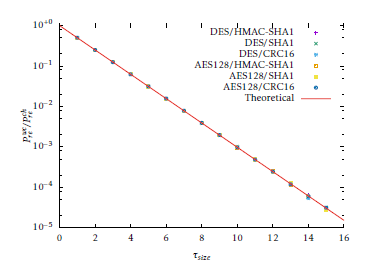Figure 4: Normalised average P_re obtained through simulation and from equation 9, for different values of τ_size.

In Figure 4 the normalised P_re is plotted, both resulting from equation 9 and from simulations. The correspondence between the theoretical model and the simulation results is very good, and the results are independent either from the H algorithm used to compute τ and the encryption algorithm ENC. Only a small glitch is visible for τ_size = 14, presumably due to the relatively small number of iterations. The simulations results are accurate because all the P_re are averaged over the pairs (k,m).

In Figure 5 and 6 the normalised P_re^wc is plotted with varying τ_size. The numerical values, displayed with a continuous line, are evaluated with the algorithm described in section 5.3.2, while the simulation results are taken as the highest value of P_re among all tested (k,m). In this case the simulations do not match the theoretical model; the reason is that while the theoretical model assumes that (k^wc,m^wc) is known, in practice this is not true, although for some ciphers it could be feasible to calculate it. In this case a great number of (k,m) combinations are randomly chosen and the worst case is considered. However, being unable to scan all the (k,m) space, it is unlikely to find the worst case but only a ”bad“ pair (k,m) is found, for which P_re differ significantly from the average case.

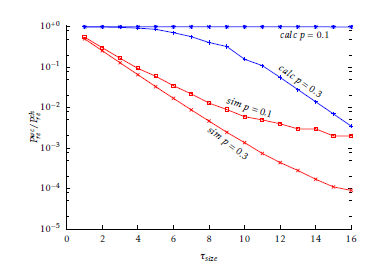Figure 5: Normalised worst-case P_re obtained with E⁰ ∼ B(n,k,p) through calculation and simulation using a DES/SHA1 scheme, with µ_size + τ_size = 64, for different values of τ_size.

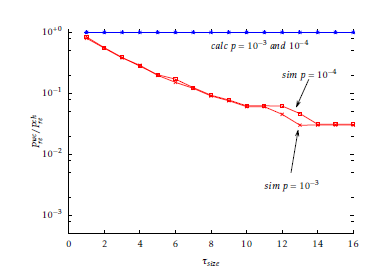Figure 6: Normalised worst-case P_re obtained with E⁰ ∼ B(n,k,p) through calculation and simulation using a DES/SHA1 scheme, with µ_size + τ_size = 64, for different values of τ_size.

In Figure 7 and 8 the normalised P_re^wc is plotted with varying p. For low values of p, the value of P_re^wc does not change a lot, since the most probable error patterns are always the ones with 1 bit error. On the other hand, with higher p the value of P_re^wc approaches _avg

P_re , which is reached with p = 0.5, corresponding to a uniform distribution. The issue of finding the worst case (k,m) is then different depending on the bit error probability of B(n,k,p). For low p, approximately under 0.1, it is easier to find a pair (k,m) with high P_re since the most probable error patterns are the ones with only 1 bit error and are exactly µ_size + τ_size. On the other hand, for higher p, the most probable error patterns are a much great number, because it is easier to find more than one bit error. This explains the difficulty of finding the pair (k^wc,m^wc) to simulate P_re^wc accurately.

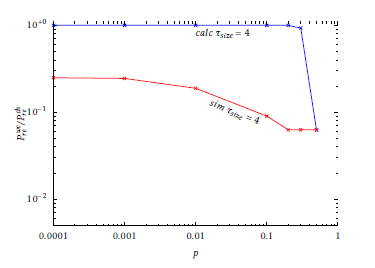Figure 7: Normalised worst-case P_re obtained with E⁰ ∼ B(n,k,p) through calculation and simulation using a DES/SHA1 scheme, with µ_size + τ_size = 64, for different values of p.

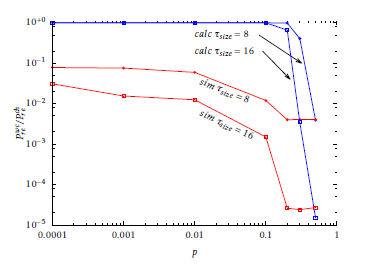Figure 8: Normalised worst-case P_re obtained with E⁰ ∼ B(n,k,p) through calculation and simulation using a DES/SHA1 scheme, with µ_size + τ_size = 64, for different values of p.

6. Discussion

Scheme Resists to Security properties Leaking out Safety properties ENC + MAC Fully Malicious with chosen plaintext Confidentiality Authentication Integrity – Strongly depends on (k,m) ENC + CRC Fully Malicious with chosen plaintext Confidentiality Integrity – Strongly depends on (k,m) plain + MAC Fully Malicious Authentication Integrity Plaintext to FM and HBC attackers Depends on H() plain + CRC Honest-But-Curious – Plaintext to FM and HBC attackers Good under common channel assumption [13] plain – – Plaintext to FM and HBC attackers – Table 2: Summary of message protection schemes.

In Table 2 different message protection schemes are compared and ordered with decreasing security properties. The message protection schemes addressed in this paper correspond to the ENC+MAC and ENC+CRC schemes, depending on the choice of H(), to resist a fully malicious attacker with chosen plaintext. The main alternative scheme, which does not consider the Confidentiality property, is evaluated for reference, based on literature work. Here the trade-off appears clear comparing the ENC+CRC and plain+CRC scheme; while the first has better security properties, the latter has better safety properties under common channel models, because CRC codes are designed specifically for correcting transmission errors.

7. Conclusion

In this paper, we have presented an analysis showing that a security property, like encryption, directly influences the probability of residual error, which is a safety property. On the other hand, the restricted size of the CAN bus payload forces the length of a MAC code to respect the fragmentation constraints which can be imposed by real-time requirements. With respect to similar schemes without encryption, by using a second CRC in addition to that one at the physical layer, the combination ENC+CRC performs worse; this is due to the intrinsic properties of block ciphers, which transform the distribution of errors to uniform on average. Other message protection schemes could have a less drastic impact on the worst-case error detection capability, or even this error detection capability could be embedded into the encryption algorithm itself, but then the risk is to offer the possibility for a side-channel attack.

Future works include the design and study of different message protection schemes, to offer a better trade-off between safety and security, for example improving the performance of the integrity tag τ with respect to transmission errors. Additionally, an experimental testbed on a real CAN bus would be useful to assess the performance of the protocol.

Conflict of Interest

The authors declare no conflict of interest.

Acknowledgement

This work has been partially supported by the GAUSS (MIUR, PRIN 2015) and by the H2020 EU funded NeCS (GA 675320).

1. Fortino, A. Rovella, W. Russo, C. Savaglio, “On the Classification of Cyberphysical Smart Objects in the Internet of Things” in Proceedings of the 5th International Workshop on Networks of Cooperating Objects for Smart Cities (UBICITEC 2014), Berlin, Germany, Apr 14, 2014, pp. 86-94.
2. Aloi, G. Caliciuri, G. Fortino, R. Gravina, P. Pace, W. Russo, C. Savaglio, “Enabling IoT interoperability through opportunistic smartphone-based mobile gateways” in Journal of Network and Computer Applications, Volume 81, 2017, Pages 74-84. https://doi.org/10.1016/j.jnca.2016.10.013
3. Valasek and C. Miller, “Remote Exploitation of an Unaltered Passenger Vehicle” in DEFCON 23, 2015.
4. Greenberg, “After jeep hack, chrysler recalls 1.4m vehicles for bug fix,” Online, Jul 2015. [Online]. Available: https://www.wired.com/2015/07/jeep-hack-chryslerrecalls- 1-4m-vehicles-bug-fix/
5. McCluskey, “Connected cars: the security challenge for autonomous vehicles,” IET Engineering and Technology Magazine, Feb 2017. [Online]. Available: https: //eandt.theiet.org/content/articles/2017/02/connectedcars- the-security-challenge-for-autonomous-vehicles/
6. Kim, “Safety challenges for connected cars,” IEEE Transportation Electrification Newsletter, Jun 2016. [Online]. Available: http://tec.ieee.org/newsletter/june-2016/safetychallenges- for-connected-cars
7. Dariz, M. Selvatici, M. Ruggeri, G. Costantino, and F. Martinelli, “Trade-off analysis of safety and security in CAN bus communication,” in 5th IEEE International Conference on Models and Technologies for Intelligent Transportation Systems, MT-ITS 2017, Naples, Italy, June 26-28, 2017, pp. 226–231. [Online]. Available: https://doi.org/10.1109/MTITS.2017.8005670
8. R. Chowdhury and S. DasBit, “Lmac: A lightweight message authentication code for wireless sensor network,” in 2015 IEEE Global Communications Conference (GLOBECOM), Dec 2015, pp. 1–6. [Online]. Available: https://doi.org/10.1109/ GLOCOM.2015.7417118
9. Mouha, B. Mennink, A. Van Herrewege, D. Watanabe, B. Preneel, and I. Verbauwhede, Chaskey: An Efficient MAC Algorithm for 32-bit Microcontrollers. Cham: Springer International Publishing, 2014, pp. 306–323. [Online]. Available: http://dx.doi.org/10.1007/978-3-319-13051-4 19
10. Ferguson, “Authentication weaknesses in gcm,” Comments submitted to NIST Modes of Operation Process, May 2005.
11. Gong, P. Hartel, S. Nikova, S.-H. Tang, and B. Zhu, “Tulp: A family of lightweight message authentication codes for body sensor networks,” Journal of Computer Science and Technology, vol. 29, no. 1, pp. 53–68, 2014. [Online]. Available: http://dx.doi.org/10.1007/s11390-013-1411-8
12. M. Fouda, Z. M. Fadlullah, N. Kato, R. Lu, and X. S. Shen, “A lightweight message authentication scheme for smart grid communications,” IEEE Transactions on Smart Grid, vol. 2, no. 4, pp. 675–685, Dec 2011. [Online]. Available: http://dx.doi.org/10.1109/TSG.2011.2160661
13. Schiller and T. Mattes, “Analysis of nested crc with additional net data by means of stochastic automata for safetycritical communication,” in 2008 IEEE International Workshop on Factory Communication Systems, May 2008, pp. 295–304. [Online]. Available: http://dx.doi.org/10.1109/WFCS.2008. 4638714
14. Barenghi, L. Breveglieri, I. Koren, and D. Naccache, “Fault injection attacks on cryptographic devices: Theory, practice, and countermeasures,” Proceedings of the IEEE, vol. 100, no. 11, pp. 3056–3076, Nov 2012. [Online]. Available: http: //dx.doi.org/10.1109/JPROC.2012.2188769
15. Rimoldi, “On algebraic and statistical properties of aeslike ciphers,” Ph.D. dissertation, University of Trento, 2010. [Online]. Available: http://eprints-phd.biblio.unitn.it/151/
16. Vaudenay, “Security flaws induced by cbc padding – applications to ssl, ipsec, wtls …” in Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques: Advances in Cryptology, ser. EUROCRYPT ’02. London, UK, UK: Springer-Verlag, 2002, pp. 534–546. [Online]. Available: http://dl.acm.org/citation.cfm?id=647087.715705
17. Vanhoef and F. Piessens, “Key reinstallation attacks: Forcing nonce reuse in WPA2,” in Proceedings of the ACM SIGSAC Conference on Computer and Communications Security (CCS). ACM Press, Nov. 2017, pp. 1313–1328. [Online]. Available: http://dx.doi.org/10.1145/3133956.3134027
18. Dworkin, “Recommendation for block cipher modes of operation: The cmac mode for authentication,” NIST Special Publication 800-38B, May 2005.
19. ISO, “Earth-moving machinery – machine-control systems (mcs) using electronic components – performance criteria and tests for functional safety,” The International Organization for Standardization, Gen`eve, Switzerland, Tech. Rep. ISO 15998, 2008.
20. Petit, F.-X. Standaert, O. Pereira, T. G. Malkin, and M. Yung, “A block cipher based pseudo random number generator secure against side-channel key recovery,” in Proceedings of the 2008 ACM Symposium on Information, Computer and Communications Security, ser. ASIACCS ’08. New York, NY, USA: ACM, 2008, pp. 56–65. [Online]. Available: http://doi.acm.org/10.1145/1368310.1368322
21. Grassi, “New approaches for distinguishers and attacks on round-reduced aes,” Cryptology ePrint Archive, Report 2017/832, 2017, http://eprint.iacr.org/2017/832.
22. Koopman, “Best crc polynomials,” 2017, https://users.ece. cmu.edu/_koopman/crc/.

(Click to view)

(Click to view)