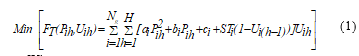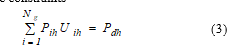1. Introduction

The main role of energy management is to ensure the production of active power in order to respond to the demand growth among a very little fuel cost [1,2]. Solving the Unit Commitment Problem (UCP) is very essential in electrical network planning. It can both optimize the daily operational planning of networks and reduce the total production cost among the improvement of the operating state of each unit leading to obtain the best unit commitment scheduling helping to respond to the power demand. Operations scheduling production units or Unit Commitment (UC) improve operational planning of the electrical grid while ensuring continuity of service [1-6]. The main purpose of solving the Unit Commitment problem is to schedule production units to respond to the consumed power with the minimization of the total production cost. The optimal planning [7-9] involves ensuring a better use of available generators subject to various constraints and guaranteeing the transfer of electrical energy from generating stations to the load. UC must satisfy the load demand, storage capability, minimum downtime startup and safety limits for each production unit.

The production scheduling comprises determining startup and each generation level for each unit in a given planning period [10-13]. Therefore, a study of literature [14,15] on methods which focus on unit commitment (UC) problem resolution shows that various optimization methods have examined this subject. Furthermore, Sasaki et al. demonstrated the possibility to use artificial neural network (ANN) to solve the UCP in which a large number of inequality constraints is processed. They have used the ANN to schedule generators and the dynamic programming to solve the load flow problem. The adopted strategy was compared to Lagrangian Relaxation (LR) and dynamic programming (DP) methods and the results offered a faster and cheaper solution compared to the LR and DP but it suffers from digital convergence because of the learning process. Certain works [16, 17] proposed a strategy based on tabu search method. They introduced new rules to generate an initial solution feasible to solve the Unit Commitment problem. This strategy consists on dividing the problem into two problems: the first combinatorial optimization problem is solved using tabu search algorithm and the second is a problem of nonlinear programming solved through the quadratic programming routine. The structure resolution through Tabu search method is similar to that used by simulated annealing [18] even though TS is provided with a simplified configuration, so it is easy to pass from one optimization to the other. Indeed, the main advantage of the adopted strategy is to extend the search space provided for the best optimal solutions which are stored in the tabu list. This method has provided a lower production cost solution, but it’s slower compared to the Lagrangian relaxation. However, T. Logenthiran et al. [19] have proposed a new approach based on particle swarm optimization (PSO) algorithm for solving the unit commitment problem. They presented three versions of particle swarm: binary particle swarm optimization (BPSO), improved binary particle swarm optimization (IBPSO) and combined use of particle swarm optimization and Lagrangian relaxation programming (LR-PSO) .The numerical results show that LR-PSO method has provided a lower production cost solution compared to LR, BPSO and IBPSO especially when the number of units important. Whereas, if the number of units is small, BPSO is taken as the best method since it has the lowest production cost compared to other algorithms. Other works, [20, 21] presented new approaches based on artificial intelligence to solve the UCP. The adopted approach combines two methods: tabu search and neural networks (ANN-TS) in order to get an optimal unit commitment scheduling allowing a minimal production cost in accordance to the constraints of the studied system. Artificial Neural networks provide a fast convergence to optimal solutions but it takes a lot of memory space because of the great number of constraints.

Cheng et al. [22] proposed a hybrid method based on the integration of the genetic algorithm in Lagrangian Relaxation Programming (LR-GA) to solve the problem of the planning of the operations of the production units. This integration consists in improving the Lagrange multipliers using the operators of the genetic algorithm to find a fast and an effective cost solution respecting all the constraints of the system. The implementation of this method requires two steps ; the first is to look for the minimum constraints of the Lagrange function under the multipliers constraint through dynamic programming. The second step consists on maximizing Lagrange’s function while respecting the multiplier adjusted by the genetic algorithms. The experimental result of this method provides a faster and cheaper solution compared to the Lagrangian relaxation method (LR) and the tabu search method (TS). However, C. Christober et al. [23] presented a hybrid method combining the evolutionary programming the tabu search methods (EP-TS). The first has the advantage of a good convergence property, a significant acceleration based on the principle of traditional genetic algorithm and a high quality of solutions, but its major disadvantage is related to the dimensioning of the Unit Commitment problem. Tabu search method improves the status by avoiding imprisonment in the local minimum. The best solution is chosen by evolutionary strategy. Thus, the effort has been made to combine these two methods whose purpose is to meet the requirements of the generators commitment problem. The numerical results demonstrate that this method is efficient and accurate in terms of calculation time and minimization of the total production cost compared to the following methods: simulated annealing, taboo search, dynamic programming, evolutionary programming, Lagrange programming and LR- GA. By contrast, Kumar et al. [24] presented a hybrid method combining dynamic programming with Hopfield Neural Networks (DP-HNN). The proposed process consists on two steps: use of Hopfield neural networks from direct computation to generate the economic distribution (ED) and use of dynamic programming (DP) to plan generators. This approach provides a poor final solution in total of production cost over other methods, but is faster than LR, DP, GA, LR-GA and AS-GA. In addition, C. Asir et al. [25] presented a new approach based on artificial intelligence to solve the problem of allocation of units. This combines two methods: tabu research and Artificial Neural Networks (ANN-TS) and this in order to have an optimal solution that solves the problem of planning power with a minimum of total production cost with respecting all the constraints of the specified system. Neural networks provide a fast convergence solution but the programming of the algorithm takes up a lot of memory space because of the constraints of the problem. The tabu search is characterized by the flexibility of its memory and it is able to find good solutions. This algorithm gave a faster and cheaper result compared to tabu search, dynamic programming, Artificial neural networks, Lagrange programming, LR-GA, TS-GA and EP-TS methods. In addition, C. Asir [26] has developed another strategy which consists in integrating the tabu search with the genetic algorithm. The purpose of this technique is to find the planning of the production. This strategy depends on the exploitation of the total cost which can be minimized when it is subjected to a set of constraints. Tabu search can find good solutions using the tabu list while genetic algorithm is used to generate new solutions using its operators. The results demonstrate that this technique provides a low cost but slow solutions compared to ANN-TS. Alma et al. [27] proposed a hybrid approach combining fuzzy logic and the genetic algorithm (FL-AG) to solve the Unit Commitment problem. Genetic algorithm uses the actual coded chromosomes in contradiction with the most commonly used scheme which is binary coding. This method uses a strict priority order list in the genetic algorithm that generates different solutions. This list serves to reduce the size of the search space of the problem, while fuzzy optimization guides the entire search process in an uncertain environment (varying from load demand, renewable energy sources etc … ).The results of this technique offer a good final solution compared to dynamic programming and to the genetic algorithm.

According to our study, we thought to validate an approach to apprehend the whole unit commitment problem. To achieve this objective, our strategy for solving the Unit Commitment Problem is based on the combination of three stochastic optimization methods that are the Particle Swarm Optimization (PSO), the Tabu Search (TS) and Lagrangian Relaxation (LR) method in order to develop a proper unit commitment scheduling of the production units to minimize the production cost.

2. Notation

The notation used throughout the paper is stated below.

: Coefficients of the production cost,

         : Active power generated by the unit  hour, and

         : On/Off status of the production unit at the  hour,  for the off state of one generating unit and  for the operating status of one generating unit,

      : Hot start-up cost of the unit,

      : Cold start-up cost of the unit,

        : System spinning reserve at the hour,

        : Amount of the consumed power at the hour,

       : Total active losses at the hour,

     :  Minimum and maximum power produced by one     generator,

    : Maximum power produced by one generator,

   : Continuously on-time of unit .

    : Continuously down-time of unit .

     : Continuously off-time of unit ,

        : Cold start time of unit .

        : Number of generating units,

        : Time horizon for UC (h).

3. Problem Formulation

Many works have been based on an analytical statement of the unit commitment problem [2,3,11, 18, 22]. We present in this paper a mathematical model of the unit commitment problem with limited security. This model is a mixed linear and constrained which has been adapted in several works [3, 9, 13, 15].

Where;

: The starting cost of the unit defined by:

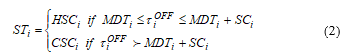The minimisation of the objective function is provided with the following constraints:

• System Constraints
• Power balance constraints

• Spinning reserve constraints

• Unit Constraints
• Genration limits

• Minimum up-time constraint

• Minimum down-time constraint

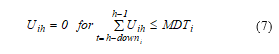4. Methodology of resolution

In this paper, four optimization methods are available to solve the unit commitment problem; the first one uses the Particle Swarm Optimization (PSO). This strategy takes into account the advantage of PSO method for solving complex and nonlinear problems. The second method relies on the use of the Tabu Search approach (TS). The use of the TS approach is depicted to the flexibility of storage great memory of optimal solutions offered by this method. The third strategy shows the advantage of the Lagrangian relaxation providing the best convergence speed. Our strategy for solving the Unit Commitment Problem is based on the combination of three optimization methods that are the Particle Swarm Optimization (PSO), the Tabu Search (TS) and Lagrangian Relaxation (LR) method to find a good On / Off states scheduling of each production unit over a period of time leading to obtain a good production cost.

4.1.  Particle Swarm Optimization

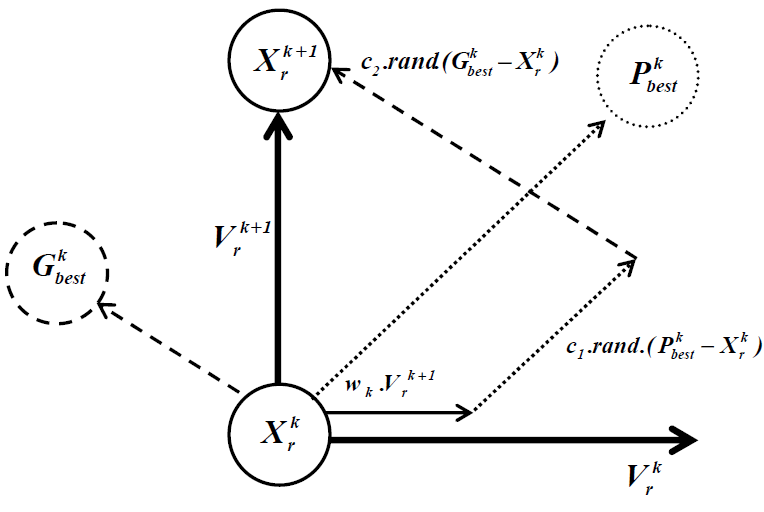
Particle swarm optimization provides a population based search procedure in which individuals called particles change their positions with time. This method is able to generate high quality of solutions within shorter calculation time and stable convergence characteristic than other stochastic optimization methods. The PSO model consists of a swarm of particles moving, figure 1, in a definite dimensional real-valued space of possible problem solutions [9,28,29].

Fig.1: PSO research process

Every particle has a position and a flight velocity . Indeed, each particle has its own best positions  and a global best position . Each time step is characterized by the update of the velocity and the particle is moved to a new position which is the sum of the previous position and the new velocity as shown in the following expression:

The update of the velocity from one particle to another is given by:

Where, et are acceleration constant, is a uniform random value between ,  and are respectively the position and the velocity of one particle  at iteration . is the inertia weight factor defined by the following equation:

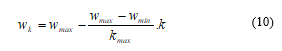Where, and are the maximum and the minimum inertia weight factors respectively and is the maximum number of iterations.

4.2.  Tabu search

Tabu search uses a local or neighborhood search procedure to iteratively move from a solution  to a solution  in the neighborhood of , until some stopping criterion has been satisfied. To explore regions of the search space that would be left unexplored by the local search procedure, TS modifies the neighborhood structure of each solution as the search     progresses [16,17]. The search for the optimal solution corresponding to minimal production cost consists on repeating an iterative process until reaching a stop criterion so as to find one solution neighbor to the optimal one as shown to the following equation:

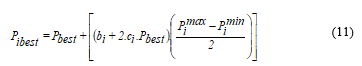The new neighborhood solutions  are determined through the use of memory structures. The search then progresses by iteratively moving from a solution  to a solution  in . To determine the solutions admitted to  , a tabu list (TL) memory is used, which is a short-term memory containing the solutions that have been visited in the recent past as less than the maximum number of iterations.

4.3.  Lagrangian Relaxation

The Lagrangian relaxation solves the Unit commitment problem by relaxing or temporarily ignoring the constraints, power balance and spinning reserve requirements [13,15,30]. Therefore, to transform the complex nonlinear constrained problem into a linear unconstrained problem, we have considered the following Lagrangian function:

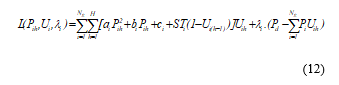Where, is the Lagrangian coefficient.

To establish our strategy, we have considered the partial derivatives of the Lagrangian function (12) with respect to each of the controllable variables equal to zero.

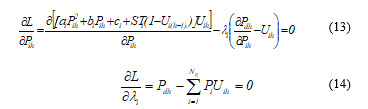Equations (13) and (14) represent the optimality conditions necessary to solve equation systems (1) and (3) without using inequality constraints (equations (4) and (5)). Equation (13) can be written as follows:

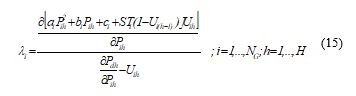4.4.  Proposed Strategy

The process of the Unit Commitment problem resolution by the combined use of Tabu search, Particle swarm optimization and Lagrangian Relaxation (TS-PSO-LR) methods is carried out according to the flowchart in Figure 2.

      The proposed strategy not only helps to reach the optimal solution as quickly as possible using the speed of the Lagrangian relaxation but also to proceed through PSO method to search effective solutions corresponding to a minimum production cost and this is obtained through a specific determination of the new velocity and then the next best position corresponding to the best amount of generated power produced by each unit when it’s in the ON state.

In the proposed method, it’s notable that representing the best information of each particle and the history of each generated power  of each production unit is preserved in the list . Herein, in spite of the possibility of the PSO method with the solution better than  around , there is the possibility not to be searched enough that’s why we have thought to use the history of in .

Fig.2: Flowchart of solving the unit commitment problem via Tabu Search, Particle Swarm Optimization and Lagrangian Relaxation

Whenever the particles lose the searching ability when the velocity of one particle is very small, the TS-PSO-LR algorithm adapts the other instead of to update equation of velocity. This action increases the searching ability and helps to find more optimal solutions enabling a minimal production cost while considering a best unit commitment scheduling.

The proposed TS-PSO-LR strategy differs from other evolutionary computing techniques in providing an acceptable solution within a relatively short time and is likely to lead the search towards the most promising solution area.  A step-by-step TS-PSO-LR for the optimization of the UC problem is outlined as follows:

Step 1: Initialization data for each unit production

Step 2: Create tabu lists

Step 3: Generate the position and the velocity ( , ) of each particle according to equations (8) and (9).

Step 4: Evaluation of each particle at an initial power value selected from the limit margins.

Step 5: Calculate the production cost function of each particle for each production unit,

Step 6: Calculate the Lagrangian coefficient according to the expression (15),

Step 7:  Calculate the objective function of each particle according to equation (1),

Step 8:  Save the best results in the tabu list

Step 9: If the stop criterion is satisfactory, the found values are those which corresponds to the desired optimal solution otherwise we return to step 3.

5. Simulation And Results

In order to test the performance of the optimization proposed method; the strategy has been applied to an IEEE electrical network 9 buses [13,15,31], having 3 generators, over a period of 48 hours. The characteristics of the different production units are given in Table 1.

Table 1: Characteristics of production units

U	(MW)	(MW)	a	b	c	M U T	M D T	($)	($)
1	582	110	0.0756	30.36	582	8	8	4500	9000
2	330	74	0.00031	17.26	970	8	8	5000	10000
3	115	25	0.00211	16.5	680	5	5	560	1120

In this paper, we have considered 48 successive periods in order to establish the temporal evolution of the power demand (Table 2).

Table 2: Amount of load required

H	Load  (MW)	H	Load  (MW)	H	Load  (MW)	H	Load  (MW)
1	353.2	13	993.2	25	833.2	37	682.2
2	378.5	14	913.2	26	813.2	38	715.2
3	463.2	15	853.2	27	763.2	39	773.2
4	573.2	16	725.2	28	713.2	40	843.2
5	628.2	17	613.2	29	626.2	41	883.2
6	693.2	18	580.2	30	547.2	42	911.2
7	713.2	19	673.2	31	503.2	43	945.2
8	753.2	20	730.2	32	473.2	44	960.2
9	843.2	21	835.2	33	433.2	45	1001.2
10	925.2	22	945.2	34	533.2	46	1003.2
11	963.2	23	1007.2	35	583.2	47	925.2
12	1013.2	24	893.2	36	627.2	48	823.2

Table 3: Comparative table of the different methods used to solve the UC problem H  (MW) Production Cost ($) Unit Commitment scheduling LR PSO TS PSO-TS-LR LR PSO TS PSO-TS-LR 1 353.2 23000 14198 14012 3424 111 111 111 111 2 378.5 25000 12981 15396 13504 111 111 111 110 3 463.2 29000 19729 20582 13261 111 111 111 110 4 573.2 375000 20320 28638 15693 111 110 111 110 5 628.2 845000 25275 33228 19913 110 110 111 110 6 693.2 1278000 32907 39192 28268 110 110 111 110 7 713.2 1432000 33600 41136 19099 110 110 111 111 8 753.2 1770000 43686 45172 25722 110 110 111 111 9 843.2 2688000 44498 50251 32251 110 110 111 111 10 925.2 7267000 46943 51667 41758 111 111 111 111 11 963.2 8441000 52566 52325 46546 111 111 111 111 12 1013.2 10129000 53198 53197 53172 111 111 111 111 13 993.2 9434000 53198 53197 50477 111 111 111 111 14 913.2 6915000 51897 49806 40681 111 111 111 111 15 853.2 2804000 37910 47580 33298 110 111 110 111 16 725.2 1529000 25883 46852 29262 110 111 110 110 17 613.2 758000 21020 46852 25554 110 111 110 110 18 580.2 584000 16014 46852 14909 110 111 110 110 19 673.2 1134000 29433 47666 23751 110 111 110 110 20 730.2 1571000 32618 49493 33494 110 111 110 110 21 835.2 2597000 38861 53197 42276 110 111 110 110 22 945.2 7873000 52140 53197 50791 111 111 111 111 23 1007.2 9918000 53198 53197 52967 111 111 111 111 24 893.2 6349000 51158 53197 37898 111 111 111 111 25 833.2 4797000 35703 53197 45178 111 111 111 111 26 813.2 4327000 36113 48240 28933 111 111 111 111 27 763.2 1861000 28794 47371 24434 111 111 110 111 28 713.2 1432000 25401 46852 29117 111 111 110 111 29 626.2 833000 46373 43893 38959 110 110 110 101 30 547.2 432000 20724 43893 31753 110 110 100 101 31 503.2 260000 24171 43893 24453 110 110 100 101 32 473.2 30000 21804 43893 21221 110 110 100 101 33 433.2 28000 25661 43893 17202 110 110 100 101 34 533.2 33000 29609 46499 30381 111 110 100 101 35 583.2 485000 45736 46499 33614 111 110 101 101 36 627.2 1017000 31241 46499 39093 111 110 101 101 37 682.2 1198000 46649 53197 22191 111 110 101 111 38 715.2 1448000 36247 53197 26763 111 111 111 111 39 773.2 1955000 35234 53197 29056 110 111 111 111 40 843.2 2688000 39180 53197 32182 110 111 111 111 41 883.2 3169000 42243 53197 36731 110 111 111 111 42 911.2 6857000 51986 53197 40051 110 111 111 111 43 945.2 7873000 52083 53197 52034 110 111 111 111 44 960.2 8345000 50398 53197 51313 110 111 111 111 45 1001.2 9709000 53198 53197 52755 110 111 111 111 46 1003.2 9778000 53198 53197 52831 111 111 111 111 47 925.2 7267000 51916 53197 41756 111 111 111 111 48 823.2 2464000 34368 49284 30006 111 111 110 111

Simulation results shown in Table 3 have proved that the adopted optimization methods have helped to establish an appropriate On/Off scheduling operating states of the production units while respecting the time constraints.

Nevertheless, through these methods we have arrived to reach an optimal production cost. Based on Table IV, the production cost found by the hybrid method based on the combination between Tabu search, Particle Swarm Optimization and Lagrangian Relaxation methods (TS-PSO-LR) method among 48 hours is about 1.5800e+06 $ lower compared to that obtained through Tabu search (PC = 2.2350e+06 $) and through PSO (PC= 1.7813e+06 $) or through Lagrangian Relaxation (PC= 1.6405e+08$). This result shows the best performances of the adopted strategy in minimizing the production cost and proves that we can get promising results through hybridization.

Table 4: Production Cost and Time required to converge for each optimized method

	TS	PSO	LR	TS-PSO-LR
Production Cost ($)	2.2350e+06	1.7813e+06	1.6405e+08	1.5800e+06
Time (s)	1.536 s	2.432s	4539s	127.082 s

Furthermore, concerning the resolution time, TS and PSO methods has presented the best time of convergence to an optimal solution compared to our strategy which requires 127.082 s to reach the global optimum. Besides, through Lagrangian Relaxation method, the unit commitment problem requires a lot of time to converge and this is explained by the complexity of the problem.

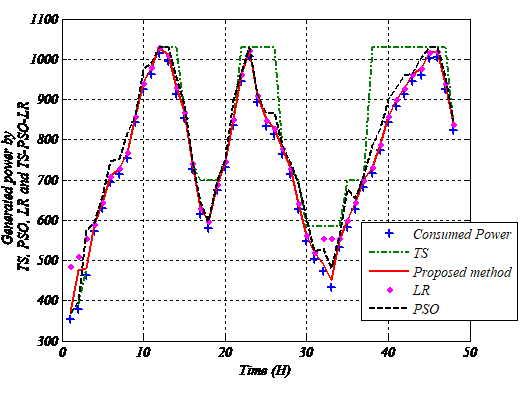Fig.3: Generated power by TS, PSO, LR and TS-PSO-LR methods

It is interesting to note that the generated powers follow the optimum power quantities provided by the proposed optimization algorithm and the other optimization method. This demonstrates the high performance of the control algorithms adopted for the supervision of the system studied and proves the efficiency of the regulation loops for the different production units. In addition, the strategy adopts a permit to obtain sufficient and rapid planning in terms of convergence. Indeed, with the particular attention we offer you the considerable choice of input variables to particle swarm optimization method, we have managed via the proposed strategy to optimize the optimal solutions able to reduce the total cost of production.

Based on the results set out in Table 4, we find that our strategy has solved the Unit Commitment problem while addressing a planning of on-off states of production units. Planning that has complied with the constraints of each unit (minimum start-up and shut-down times ). Moreover, we note that the power produced by the most powerful machine (615 MVA) remains unchanged throughout the 48 hours while the other production units vary to produce the amount of power demanded by the network.

Thanks to the simulation results, we can note that the Unit Commitment scheduling found by the hybrid approach has helped to obtain the minimum production cost compared to the other monotonous methods. This proves the main feature of the hybridization technique [32] that allows the combination of the advantages of various methods. Indeed, the tabu search, as table 4 shows, is found the most efficient regarding the convergence time but it has the highest total production cost. As for the Lagrangian relaxation, has allowed to have a very high production cost and requires a considerable time to converge. Whereas, the particle swarm optimization is conducted in a good convergence time but the cost is high compared to our TS-PSO-LR strategy. This comparison reflects the performance of the hybrid strategy, both in production cost and in convergence time.

Therefore, based on Figure 3, we can notice that the total amount of generated power by the production units is very similar to that consumed with a very limited amount of spinning reserve power compared to PSO, TS and LR methods where the generated powers are much higher than the amount requested. This proves the effectiveness of tracking of the consumed power per each hour and shows the performance of the algorithms enabling to get a minimal production cost. Besides, this minimal production cost has been established thanks to a good On/Off statements scheduling set for each production units (Figures 4 and 5). The organization is made through an estimation of the amount of load desired by the electric network, while taking into account of the allowable constraints.

We note that the optimal unit commitment scheduling found by our PSO-TS-LR strategy is characterized by the On status of the powerful unit (615 MVA) [3,6,8,9,13] throughout 48 hours and this is due to the minimum up and the minimum down-time constraints and to the power demand governed for each hour. We note that the unit commitment scheduling of the second production unit (370 MVA) is respecting the during minimum up/down time equal to 8 hours which proves the effectiveness of the control

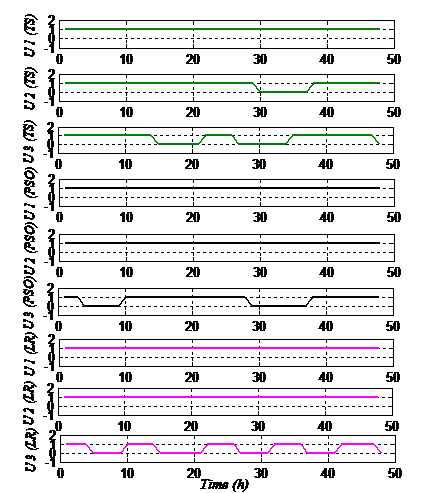Fig.4: Optimal binary combination of units operation through TS method, PSO method and LR method

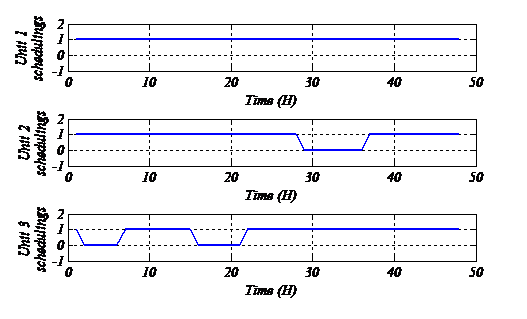Fig.5: Optimal binary combination of units operation through hybrid TS-PSO-LR method

strategy. The third production unit undergoes Off status according to the production requirement and according to the power demand.

Furthermore, we confirm that our approach has allowed to select precisely the production units that should be available to respond to the load demand of the electrical network over a future period.

In addition, the adopted approach was promising both in terms of convergence to get the best optimal solutions to minimize the production cost and for an efficient unit commitment scheduling for the different production units, figure 6. Our strategy differs from other evolutionary computing techniques in providing an acceptable solution within a relatively short time and is likely to lead the search towards the most promising solution area.

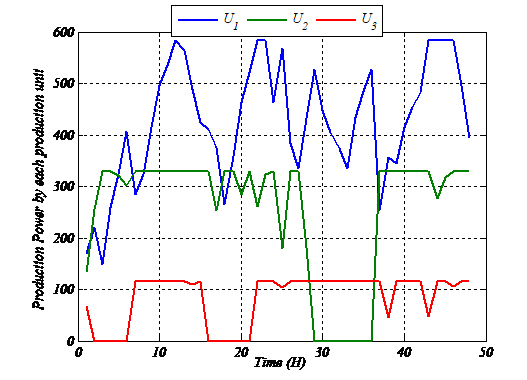Fig.6: Generated Power by each production unit during 48 hours

6. Conclusion

This work shows the implementation of a new hybrid strategy which combines between Tabu Search, Particle Swarm Optimization and Lagrangian Relaxation. Herein, we have benefited from the rapidity of Lagrangian relaxation method, the storage solution with the memory of Tabu Search method and the flexibility to find optimal solution given by the Particle Swarm Optimization method. The proposed strategy TS-PSO-LR has presented high performances in optimizing the production cost and a capability of convergence to a global optimum as quick as possible compared to meta-heuristic (PSO, TS) and deterministic (LR) methods. In addition, the proposed strategy has ensured a proper unit commitment scheduling leading to get a minimal production cost. The right choice of the initial population suggests the possibility to obtain improvements in execution time. In addition, our strategy provides a fast enough time to converge to the optimal solution; which demonstrates the effectiveness of the adopted strategy compared to that obtained by Lagrangian Relaxation method and Particle swarm optimization methods.

Conflict of Interest

The authors declare no conflict of interest.

1. Merlin, A., Sandrin, P. (1983) “A new method for unit commitment at Electricity De France”, IEEE Trans on Power Apparatus and Systems; 102:1218-25.
2. Lin, FT., Kao, C., Hsu, C. (1993) “Applying the genetic approach to simulated annealing in solving some NP-Hard problems”. IEEE Trans on Systems, Man and Cybernetics; 23(6):1752-67.
3. Sahbi Marrouchi, Moez ben hessine and Souad Chebbi, “New strategy based on Combined Use of Particle Swarm Optimization and Gradient methods to solve the Unit Commitment Problem”, 15th IEEE International Conference on Environment and Electrical Engineering (EEEIC), Rome, Italy, 10-13 Juin 2015.
4. Chunlin, D., Liu, Y., (2014) “Sample average approximation method for the chance-constrained stochastic programming in the transportation model of emergency management”, Int. J. of Simulation and Process Modelling, Vol.9, No.4, pp.222 – 227.
5. Richard, L. W., David, H. C. (2015) “A comprehensive method for solving finite-state semi Markov processes”, Int. J. of Simulation and Process Modelling, Vol.10, No.1, pp.89 – 99.
6. Rabeh, A., Sahbi, M., Moez, B.H., Houda, J., Souad, C., (2012) “Voltage Control Strategy of an Electrical Network by the Integration of the UPFC Compensator”, International Review On Modelling and Simulation, vol. 5, no. 1, pp. 380–384.
7. Galina, M., Vitaly, B., (2014) “Integrated planning and scheduling built on cluster analysis and simulation optimization”, Int. J. of Simulation and Process Modelling, Vol.9, No.1/2, pp.81 – 91.
8. Moez, B.H., Souad, B.S, (2014 ) “Accurate Fault Classifier and Locator for EHV Transmission Lines based on Artificial Neural Networks”, Mathematical Problems in Engineering (MPE), ID 240565, vol 2014.
9. Sahbi, M., Souad, C., (2014) “Combined Use of Particle Swarm Optimization and Genetic Algorithm Methods to Solve the Unit Commitment Problem”, 16th International conference on Sciences and Techniques of Automatic control & computer engineering (STA), Monastir, Tunisia.
10. Rahul, G., and Sharma, A.K. (2008) “Economic generation and scheduling of power by genetic algorithm”, Journal of Theoretical and Applied Information Technology (JATIT).
11. Aoki, K., Satoh, T., Itoh, M., Ichimori, T., and Masegi, K. (1987) “unit commitment in a large-scale power system including fuel constrained thermal and pumped-storage hydro”, IEEE Transactions on Power Systems, Vol. PWRS-2, No. 4.
12. Ouyang, Z., Shahidehpour, S. M. (1991) “An intelligent dynamic programming for unit commitment application”, IEEE Trans on Power Systems; 6(3):1203-9.
13. Sahbi, M., Souad, C., (2014) “A Comparative Study of Fuzzy Logic, Genetic Algorithm, and Gradient-Genetic Algorithm Optimization Methods for Solving the Unit Commitment Problem”, Mathematical Problems in Engineering, vol. 2014, Article ID 708275, 14 pages, 2014. doi:10.1155/2014/708275
14. Sasaki, H., Watanabe, M., Kubokawa, Yorino, J. N. and Yokoyama, R. (1992) “A solution method of unit commitment by artificial neural network”, IEEE Transactions on Power Systems, Vol. 7, No. 3.
15. Sahbi, M., Souad, C., (2014) “Unit Commitment Optimization Using Gradient-Genetic Algorithm and Fuzzy Logic Approaches”, Complex system modeling and control through intelligent soft computations, Vol. 319, Springer book.
16. Mantawy, A. H., Youssef, Y. L., Magid, L. A., and Shokri, S. Z., Selim, Z. (1998) “A unit commitment by Tabu search,” Proc. Inst. Elect. Eng.Gen. Transm.Dist., vol. 145, no. 1, pp. 56–64.
17. H. Mantawy. L. and Abdel MagidS. Z. Selim, (1998) “A unit commitment by Tabu search’’, 1998 IEEE Proceedings online no. 1998.
18. P. Cheng, C. W. Liu, C. C. Liu. (2002) “Unit commitment by annealing-genetic algorithm, Electrical Power and Energy Systems, vol. 24 pp 149-158.
19. Logenthiran, T. and Dipti, S., (2010) ‘‘Particle Swarm Optimization for Unit Commitment Problem’’, International Conference on Probabilistic Methods Applied to Power Systems, pp 642 – 647.
20. Charles, G., Christober A. R., (2009) ‘‘Neural Based Tabu Search Method for Solving Unit Commitment Problem with Cooling-Banking Constraints’’,Serbian Journal of electrical engineering Vol. 6, No. 1, May 2009, 57-74 UDK: 004.832.2, 2009.
21. Senthil, K. and Palanisamy, V., (2006) ‘‘A New Dynamic Programming Based Hopfield Neural Network to Unit Commitment and Economic Dispatch’’ International Conference on Industrial Technology,pp 887 – 892, Mumbai.
22. Chuan-Ping Cheng, Chih-Wen Liu, and Chun-Chang Liu, ‘‘Unit Commitment by Lagrangian Relaxation and Genetic Algorithms’’, IEEE Transactions on Power Systems, vol. 15, NO. 2, MAY 2000.
23. Christober Asir Rajan and M. R. Mohan,“An Evolutionary Programming-Based Tabu Search Method For Solving The Unit Commitment Problem,” IEEE Transactions on Power Systems, VOL. 19, NO. 1, FEBRUARY 2004.
24. Senthil Kumar and V. Palanisamy, ‘‘A New Dynamic Programming Based Hopfield Neural Network to Unit Commitment and Economic Dispatch’’,IEEE Transactions on Power Systems, 2006.
25. Charles Gnanakkan Christober Asir Rajan, ‘‘Neural Based Tabu Search Method for Solving Unit Commitment Problem with Cooling-Banking Constraints’’, Serbian Journal of electrical engineering Vol. 6, No. 1, May 2009, 57-74 UDK: 004.832.2, 2009.
26. Christober C. Asir Rajan, ‘‘Genetic algorithm based tabu search method for solving unit commitment problem with cooling –– banking constraints’’, Journal of electrical engineering, vol. 60, NO. 2, 2009.
27. Alma Ademovic, Smajo Bisanovic and Mensur Hajro, ‘‘ A Genetic Algorithm Solution to the Unit Commitment Problem Based on Real-Coded Chromosomes and Fuzzy Optimization’’, IEEE Transactions on Power Systems, 2010.
28. Zhao, B., Guo, C. X., Bai, B. R.,  and Cao, Y.J. (2006) “ An improved particle swarm optimization algorithm for unit commitment”, International Journal of Electrical Power and Energy Systems, vol. 28, no. 7, pp. 482–490.
29. Raglend, I.J., Raghuveer, C., Avinash, G.R., Padhy, N.P., and Kothari, D. P. (2010) “Solution to profit based unit commitment problem using particle swarm optimization”, Applied Soft Computing Journal, vol. 10, no. 4, pp. 1247–1256.
30. Chuan,-P.C., Chih, W.L., and Chun, C.L., (2000) ‘‘Unit Commitment by Lagrangian Relaxation and Genetic Algorithms’’,IEEE Transactions on Power Systems, vol. 15, NO. 2.
31. Sahbi, M., Souad, C., (2014) “New strategy based on Fuzzy-Logic Approach to Solve the Unit-Commitment Problem”, International Conference on Control, Engineering & Information Technology (CEIT), Monastir, Tunisia.
32. Letizia, N.; Alessandro, C., Carlos, A., Rafael, D., (2014) “Hybrid approach for container terminals performances evaluation and analysis”, Int. J. of Simulation and Process Modelling, Vol.9, No.1/2, pp.104–112.

(Click to view)

(Click to view)