Numerical Solution of Fuzzy Differential Equations with Z-numbers using Fuzzy Sumudu Transforms
Volume 3, Issue 1, Page No 66-75, 2018
Author’s Name: Sina Razvarz1, Raheleh Jafari2,a), Wen Yu1
View Affiliations
1Departamento de Control Automatico CINVESTAV-IPN (National Polytechnic Institute) Mexico City 07360, Mexico
2Department of Information and Communication Technology Agder University College, 4876 Grimstad, Norway
a)Author to whom correspondence should be addressed. E-mail: jafari3339@yahoo.com
Adv. Sci. Technol. Eng. Syst. J. 3(1), 66-75 (2018); ![]() DOI: 10.25046/aj030108
DOI: 10.25046/aj030108
Keywords: K fuzzy Sumudu transform, fuzzy differential equation, Z-number
Export Citations
The uncertain nonlinear systems can be modeled with fuzzy differential equations (FDEs) and the solutions of these equations are applied to analyze many engineering problems. However, it is very difficult to obtain solutions of FDEs.
In this paper, the solutions of FDEs are approximated by utilizing the fuzzy Sumudu transform (FST) method. Here, the uncertainties are in the sense of Z-numbers. Important theorems are laid down to illustrate the properties of FST. The theoretical analysis and simulation results show that this new technique is effective to estimate the solutions of FDEs.
Received: 14 November 2017, Accepted: 17 January 2018, Published Online: 30 January 2018
1. Introduction
This paper is an extension of work originally presented in [1]. In many physical and dynamical processes, mathematical modeling leads to the deterministic initial and boundary value problems. In practical the boundary values may be different from crisp and displays in the form of unknown parameters [2]. When the parameters or the states of the differential equations are uncertain, they can be modeled with FDE. In recent days, many methods have used FDE for modeling and control of uncertain nonlinear systems [3-5]. The basic idea of the fuzzy derivative was first introduced in [Chang]. Then it is extended in [6]. The first-order fuzzy initial value problem, as well as fuzzy partial differential equation, have been studied in [7]. By generalizing the differentiability, [6] gave an analytical solution. The Lipschitz condition, as well as the theorem for existence and uniqueness of the solution related to FDEs, are discussed in [10-12]. In [13], the analytical solutions of second order FDE are obtained. The analytical solutions of third order linear FDE are found in [14]. By the interval-valued method, [15] examined the basic solutions of nonlinear FDEs with generalized differentiability.
A novel technique in order to solve FDEs is laid down based on the Sumudu transform. Sumudu transform along with broad applications has been utilized in the area of system engineering and applied physics [16-18]. In [19], some simple and deeper fundamental theorems, as well as properties of the Sumudu Transform, were generalized. In [20], Sumudu transform is applied to the system of differential equations. In [21], Sumudu transform is used in order to find the solution of the fuzzy partial differential equation. In [22], Sumudu transform has been used to solve fractional differential equations.
In this paper, we use FST to approximate the Z-number solutions of the FDEs. The FST reduces the FDE to an algebraic equation. A very important property of the FST is that it can solve the equation without resorting to a new frequency domain. The procedure of switching FDEs to an algebraic equation is cited in [10] and is stated as an operational calculus. We extend our previous work [1] by generating more theorems for describing the properties of FST and displaying the uncertainties with Z-numbers. The Z-number is a new concept that is subjected to a higher potential to demonstrate the information of the human being as well as to utilize in information processing [23]. Z-numbers can be regarded as to answer questions and carry out the decisions [24]. There exist few structure based on the theoretical concept of Z-numbers [25]. [26] gave an inception, which results in the extension of the Z-numbers. [27] generated a theorem to convert the Z-numbers to the usual fuzzy sets.
In this paper, initially, some preliminary definitions along with properties related to FST are demonstrated. After that, solving FDEs by using the methodology of FST has been discussed. At the end, two examples along with comparisons are utilized in order to demonstrate the effectiveness of our proposed method.
2. Preliminaries
Prior to the introduction of the FST, some concepts related to the fuzzy variables and Z-numbers are laid down in this section [28, 29].










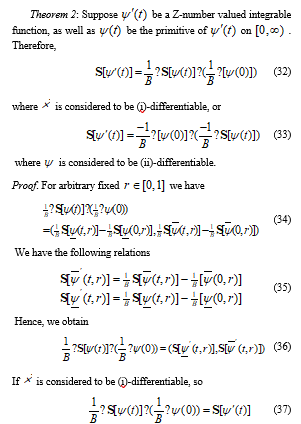
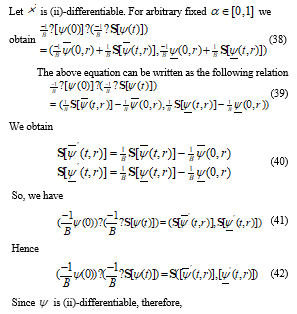


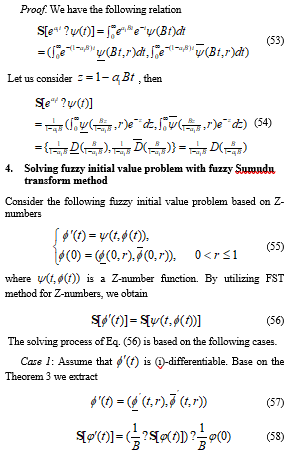



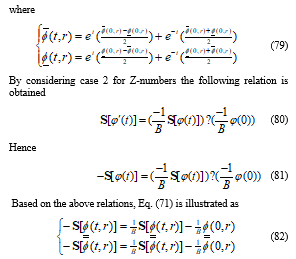


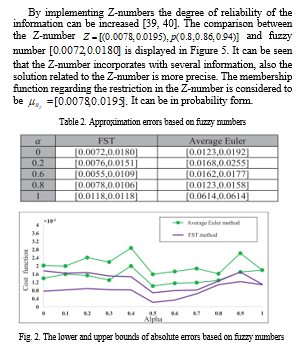
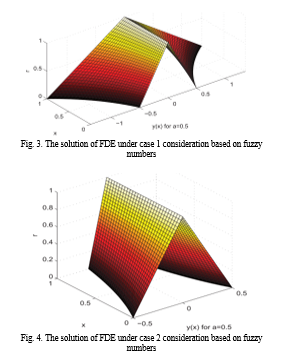
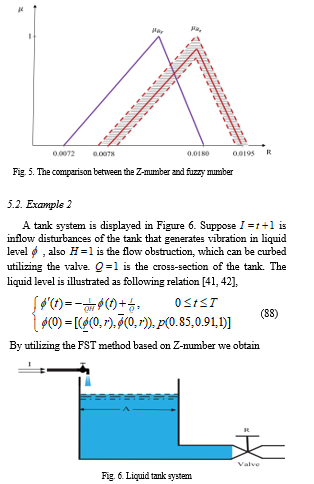
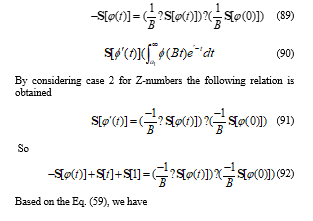

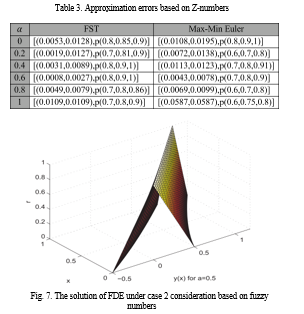
6. Conclusion
In this paper, a novel method based on the FST is proposed in order to find the solution of the first order FDEs on the basis of the Z-numbers. The new method is clarified by utilizing the concept of strongly generalized differentiability. By using the FST method, the FDE converts to an algebraic problem. Some essential theorems are laid down in order to demonstrate the properties of the FST. Two real examples are applied to demonstrate the effectiveness of the proposed technique. This work has a significant contribution in initializing a superior starting point for such extensions.
- Jafari, S. Razvarz, “Solution of Fuzzy Differential Equations using Fuzzy Sumudu Transforms” IEEE International Conference on Innovations in Intelligent Systems and Applications, 84-89, 2017. DOI: 10.1109/INISTA.2017.8001137
- Zwillinger, “Handbook of differential equations” Gulf Professional Publishing. 1998.
- Jafari, W. Yu, “Fuzzy Control for Uncertainty Nonlinear Systems with Dual Fuzzy Equations” Journal of Intelligent and Fuzzy Systems. 29(3), pp.1229-1240, 2015. DOI: 10.3233/IFS-151731
- Jafari, W. Yu, “Fuzzy Differential Equation for Nonlinear System Modeling with Bernstein Neural Networks” IEEE Access., 2017. doi:10.1109/ACCESS.2017.2647920
- Jafari, W. Yu, “Uncertainty Nonlinear Systems Modeling with Fuzzy Equations” Mathematical problems in Engineering. 2017, 2017. doi:10.1155/2017/8594738
- L. Chang, L.A. Zadeh, “On fuzzy mapping and control” IEEE Trans. Syst. Man Cybern. 2(1), 30-34, 1972. DOI: 10.1109/TSMC.1972.5408553
- Dubois, H. Prade, “Towards fuzzy differential calculus: part 3 differentiation” Fuzzy Sets Syst. 8(3), 225-233, 1982. https://doi.org/10.1016/S0165-0114(82)80001-8
- Kloeden, “Remarks on Peano-like theorems for fuzzy differential equations” Fuzzy Set Syst. 44(1), 161-164, 1991. https://doi.org/10.1016/0165-0114(91)90041-N
- Bede, I.J. Rudas, A.L. Bencsik “First order linear fuzzy differential equations under generalized differentiability” Inform. Sci. 177(7), 1648-1662, 2007. https://doi.org/10.1016/j.ins.2006.08.021
- Allahviranloo, M.B. Ahmadi, “Fuzzy Laplace Transform” Soft Computing. 14, 235-243, 2010.
- Ding, M. Ma, A. Kandel, “Existence of the solutions of fuzzy differential equations with parameters” Inform Sci. 99(3-4), 205-217, 1997. https://doi.org/10.1016/S0020-0255(96)00279-4
- A. Truong, V.H. Ngo, D.P. Nguyen, “Global existence of solutions for interval-valued integro-differential equations under generalized H-differentiability” Advances in Difference Equations. 1, 217-233, 2013. https://doi.org/10.1186/1687-1847-2013-217
- Allahviranloo, N.A. Kiani, M. Barkhor- dari, “Toward the exiistence and uniqueness of solution of second-order fuzzy differential equations” Inform. Sci. 179, 1207-1215, 2009. https://doi.org/10.1016/j.ins.2008.11.004
- Hawrra, K.H. Amal, “On fuzzy Laplace transform for fuzzy differential equations of the third order” Journal of Kerbala University, 11(3), 251-256, 2013.
- Stefanini, B. Bede, “Generalized Hukuhara differentiability of interval-valued functions and interval differential equations” J. Nonlinear Anal. (TMA). 71(3-4), 1311-1328, 2009. https://doi.org/10.1016/j.na.2008.12.005
- B.M. Belgacem, A.A. Karaballi, S.L. Kalla, “Analytical investigations of the Sumudu transform and applications to integral production equations” Math. Prob. Eng. 103(3), 103-118, 2003. http://dx.doi.org/10.1155/S1024123X03207018.
- Liu, W. Chen, “A new iterational method for ordinary equations using Sumudu transform” Advances in Analysis, 1(2), 89-94, 2016. DOI: 10.22606/aan.2016.12004
- M. Srivastava, A. Khalili Golmankhaneh, D. Baleanu, X.J Yang, “Local Fractional Sumudu Transform with Application to IVPs on Cantor Sets” Abstract and Applied Analysis. Article ID 620529, 2014.1-7, 2014. http://dx.doi.org/10.1155/2014/620529, 2014.
- B.M. Belgacem, A.A. Karaballi, “Sumudu transform fundamental properties investigations and applications” J. Appl. Math. Stoch. Anal. 2006, 1-23, 2006. http://dx.doi.org/10.1155/JAMSA/2006/91083
- Kiliçman, H. Eltayeb, R.P. Agarwal, “On Sumudu Transform and System of Differential Equations” abstr. Appl. Anal, 2010, 1-11, 2010. doi:10.1155/2010/598702.
- A. Abdul Rahman, M.Z. Ahmad, “Fuzzy Sumudu transform for solving fuzzy partial differential equations” J. Nonlinear Sci. Appl. 9, 3226-3239, 2016.
- D. Katatbeh, F.B.M. Belgacem, “Applications of the Sumudu transform to fractional differential equations” Nonlinear Studies. 18(1), 99-112, 2011.
- A. Zadeh, “Generalized theory of uncertainty (GTU)-principal concepts and ideas” Computational Statistics and Data Analysis, 51(1), 15-46, 2006. https://doi.org/10.1016/j.csda.2006.04.029
- Kang, D. Wei, Y. Li, Y. Deng, “A method of converting Z-number to classical fuzzy number” Journal of Information and Computational Science, 9(3), 703-709, 2012.
- A. Gardashova, “Application of operational approaches to solving decision making problem using Z-Numbers” Journal of Applied Mathematics, 5(9), 1323-1334, 2014. DOI: 10.4236/am.2014.59125
- A. Aliev, A.V. Alizadeh, O.H. Huseynov, “The arithmetic of discrete Z-numbers” Inform. Sci. 290, 134–155, 2015. https://doi.org/10.1016/j.ins.2014.08.024
- Kang, D. Wei, Y. Li, Y. Deng, “Decision making using Z-Numbers under uncertain environment” Journal of Computational Information Systems, 8(7), pp.2807-2814, 2012.
- Jafarian, R. Jafari, M. Mohamed Al Qurashi, D. Baleanud, “A novel computational approach to approximate fuzzy interpolation polynomials” Springer Plus, 5, pp.14-28, 2016. https://doi.org/10.1186/s40064-016-3077-5
- Jafari, W. Yu, X. Li, “Numerical Solution of Fuzzy Equations with Z-numbers using Neural Networks” Intelligent Automation and Soft Computing, 2017. doi: 10.1080/10798587.2017.1327154.
- L. Puri, D. Ralescu, “Fuzzy random variables” J. Math. Analysis Appl. 114(2), 409-422, 1986. https://doi.org/10.1016/0022-247X(86)90093-4
- -C. Wu, “The improper fuzzy Riemann integral and its numerical integration” Inform. Sci. 111(1-4), 109-137, 1999. https://doi.org/10.1016/S0020-0255(98)00016-4
- Bede, S.G. Gal, “Generalizations of the differentiability of fuzzy-number-valued functions with applications to fuzzy differential equations” Fuzzy Set Syst. 151(3), 581-599, 2005. https://doi.org/10.1016/j.fss.2004.08.001
- Chalco-Cano, H. Roman-Flores, “On new solutions of fuzzy differential equations” Chaos Solitons Fractals. 38(1), 112-119, 2006. https://doi.org/10.1016/j.chaos.2006.10.043
- A. Zadeh, “Toward a generalized theory of uncertainty (GTU) an outline” Inform. Sci. 172 (1-2), 1-40, 2005. https://doi.org/10.1016/j.ins.2005.01.017
- A. Aliev, W. Pedryczb, V. Kreinovich, O.H. Huseynov, “The general theory of decisions” Inform. Sci. 327(10), 125-148, 2016. https://doi.org/10.1016/j.ins.2015.07.055
- A. Aliev, O.H. Huseynov, R.R. Aliyev, A.V. Alizadeh, “The arithmetic of Z-numbers” Theory and applications World Scientific, Singapore, 2015.
- H. Pletcher, J.C. Tannehill, D. Anderson, “Computational Fluid Mechanics and Heat Transfer”, Taylor and Francis, 1997.
- Tapaswini, S. Chakraverty, “Euler-based new solution method for fuzzy initial value problems” Int. J. Artificial. Intell. Soft. Comput. 4(1), 58-79, 2014. https://doi.org/10.1504/IJAISC.2014.059288
- Razvarz, M. Tahmasbi, “Fuzzy equations and Z-numbers for nonlinear systems control”, Procedia Computer Science, 120, 923-930, 2017. https://doi.org/10.1016/j.procs.2017.11.327
- Jafari, W. Yu, “Uncertain nonlinear system control with fuzzy differential equations and Z-numbers”, 18th IEEE International Conference on Industrial Technology, Canada, 890-895, doi:10.1109/ICIT.2017.7915477, 2017.
- L. Streeter, E.B. Wylie, K.W. Bedford, “Fluid mechanics” New York: McGraw Hill, 1998.
- Jafari, W. Yu, X. Li, S. Razvarz, “Numerical Solution of Fuzzy Di¤erential Equations with Z-numbers Using Bernstein Neural Networks” International Journal of Computational Intelligence Systems, 10, 1226-1237, 2017. doi:10.2991/ijcis.10.1.81
Citations by Dimensions
Citations by PlumX
Google Scholar
Scopus
Crossref Citations
- Raheleh Jafari, Sina Razvarz, Alexander Gegov, "A Novel Technique to Solve Fully Fuzzy Nonlinear Matrix Equations." In 13th International Conference on Theory and Application of Fuzzy Systems and Soft Computing — ICAFS-2018, Publisher, Location, 2019.
- , "References." In Modeling and Control of Uncertain Nonlinear Systems with Fuzzy Equations and Z‐Number, Publisher, Location, 2019.
- Raheleh Jafari, Sina Razvarz, Alexander Gegov, "A New Computational Method for Solving Fully Fuzzy Nonlinear Systems." In Computational Collective Intelligence, Publisher, Location, 2018.
- Raheleh Jafari, Sina Razvarz, Alexander Gegov, "Fuzzy Differential Equations for Modeling and Control of Fuzzy Systems." In 13th International Conference on Theory and Application of Fuzzy Systems and Soft Computing — ICAFS-2018, Publisher, Location, 2019.
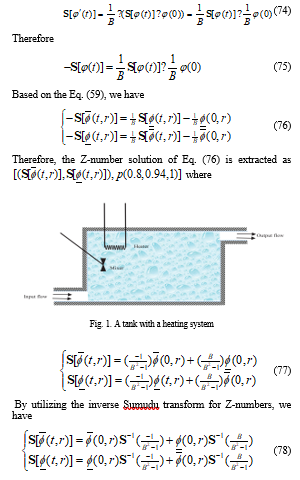
- Raheleh Jafari, Sina Razvarz, Alexander Gegov, Satyam Paul, "Modeling and Control of Uncertain Nonlinear Systems." In 2018 International Conference on Intelligent Systems (IS), pp. 168, 2018.
- Sina Razvarz, Cristobal Vargas-Jarillo, Raheleh Jafari, "Pipeline Monitoring Architecture Based on Observability and Controllability Analysis." In 2019 IEEE International Conference on Mechatronics (ICM), pp. 420, 2019.
- Sina Razvarz, Felipe Hernández-Rodríguez, Raheleh Jafari, Alexander Gegov, "Foundation of Z-Numbers and Engineering Applications." In Industrial and Robotic Systems, Publisher, Location, 2020.
- Raheleh Jafari, Sina Razvarz, Wen Yu, Alexander Gegov, Morten Goodwin, Mo Adda, "Genetic Algorithm Modeling for Photocatalytic Elimination of Impurity in Wastewater." In Intelligent Systems and Applications, Publisher, Location, 2020.
- Sina Razvarz, Raheleh Jafari, Alexander Gegov, "A Review on Different Pipeline Defect Detection Techniques." In Flow Modelling and Control in Pipeline Systems, Publisher, Location, 2021.
No. of Downloads Per Month
No. of Downloads Per Country
